Chuyên đề dạy thêm Toán 10 Cánh diều (có lời giải)

Tài liệu chuyên đề dạy thêm Toán 10 Cánh diều gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10.

Chuyên đề dạy thêm Toán 10 Cánh diều (có lời giải)

Xem thử

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Cánh diều bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Chuyên đề dạy thêm Toán 10 Cánh diều gồm 7 Chương với nhiều dạng bài đa dạng và bài tập đầy đủ các mức độ:

• Chuyên đề Mệnh đề toán học. Tập hợp

• Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

• Chuyên đề Hàm số và đồ thị

• Chuyên đề Hệ thức lượng trong tam giác. Vectơ

• Chuyên đề Đại số tổ hợp

• Chuyên đề Một số yếu tố thống kê và xác suất

• Chuyên đề Phương pháp tọa độ trong mặt phẳng

Xem thử

Chuyên đề Mệnh đề toán học. Tập hợp lớp 10 - Cánh diều

BÀI 1: MỆNH ĐỀ TOÁN HỌC

I. MỆNH ĐỀ TOÁN HỌC

- Mỗi mệnh đề phải hoặc đúng hoặc sai.

- Mỗi mệnh đề không thể vừa đúng, vừa sai.

II. MỆNH ĐỀ CHỨA BIẾN

Xét câu “$n$ chia hết cho $3$” (với $n$ là số tự nhiên).

Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề.

Tuy nhiên, nếu thay $n$ bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:

- Với $n=21$ ta được mệnh đề “21 chia hết cho 3”. Đây là mệnh đề đúng.

- Với $n=10$ ta được mệnh đề “10 chia hết cho 3”. Đây là mệnh đề sai.

Ta nói rằng câu “$n$ chia hết cho 3” là một mệnh đề chứa biến.

III. PHỦ ĐỊNH CỦA MỘT MỆNH ĐỀ

Cho mệnh đề $P$. Mệnh đề “Không phải $P$” được gọi là mệnh phủ định của mệnh đề $P$ và kí hiệu là $\overline{P}$. Khi đó, ta có:

+ $\overline{P}$ đúng khi $P$ sai.

+ $\overline{P}$ sai khi $P$ đúng.

IV. MỆNH ĐỀ KÉO THEO

- Mệnh đề $"$Nếu $P$ thì $Q$$"$ được gọi là mệnh đề kéo theo, và kí hiệu là $P\Rightarrow Q.$

- Mệnh đề $P\Rightarrow Q$ còn được phát biểu là "$P$ kéo theo $Q$" hoặc " Từ $P$ suy ra $Q$"

- Mệnh đề $P\Rightarrow Q$ chỉ sai khi $P$ đúng và $Q$ sai.

Như vậy, ta chỉ xét tính đúng sai của mệnh đề $P\Rightarrow Q$ khi $P$ đúng. Khi đó, nếu $Q$ đúng thì $P\Rightarrow Q$ đúng, nếu $Q$ sai thì $P\Rightarrow Q$ sai.

- Các định lí, toán học là những mệnh đề đúng và thường có dạng $P\Rightarrow Q.$

Khi đó ta nói $P$ là giả thiết, $Q$ là kết luận của định lí, hoặc $P$ là điều kiện đủ để có $Q$ hoặc $Q$ là điều kiện cần để có $P$

V. MỆNH ĐỀ ĐẢO – HAI MỆNH ĐỀ TƯƠNG ĐƯƠNG

Mệnh đề $Q\Rightarrow P$ được gọi là mệnh đề đảo của mệnh đề $P\Rightarrow Q.$

Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.

Nếu cả hai mệnh đề $P\Rightarrow Q$ và $Q\Rightarrow P$ đều đúng ta nói $P$ và $Q$ là hai mệnh đề tương đương.

Khi đó ta có kí hiệu $P\iff Q$ và đọc là $P$ tương đương $Q,$ hoặc $P$ là điều kiện cần và đủ để có $Q,$ hoặc $P$ khi và chỉ khi $Q.$

VI. KÍ HIỆU $\forall$ VÀ $\exists$

Ví dụ: Câu "Bình phương của mọi số thực đều lớn hơn hoặc bằng 0" là một mệnh đề. Có thể viết mệnh đề này như sau

$\forall x\in ℝ:x^2\ge 0$ hay $x^2\ge 0,\forall x\in ℝ.$

Kí hiệu $\forall$ đọc là "với mọi"

Ví dụ: Câu "Có một số nguyên nhỏ hơn 0" là một mệnh đề.

Có thể viết mệnh đề này như sau:

$\exists n\in \mathbb{Z}:n<0.$

Kí hiệu $\exists$ đọc là "có một" (tồn tại một) hay "có ít nhất một" (tồn tại ít nhất một).

- Mệnh đề phủ định của mệnh đề $"\forall x\in X,P\left(x\right)"$ là $"\exists x\in X,\overline{P\left(x\right)}".$

Ví dụ: Cho mệnh đề:

$“\forall x\in ℝ,x^2-x+7<0”$.

Tìm mệnh đề phủ định của mệnh đề trên?

Lời giải

Phủ định của mệnh đề:

$“\forall x\in ℝ,x^2-x+7<0”$ 

là mệnh đề: $“\exists x\in ℝ,x^2-x+7\ge 0”$.

Mệnh đề phủ định của mệnh đề $"\exists x\in X,P\left(x\right)"$ là $"\forall x\in X,\overline{P\left(x\right)}".$

Ví dụ: Cho mệnh đề:

$“\exists x\in ℝ,x^2-x-6=0”$.

Tìm mệnh đề phủ định của mệnh đề trên?

Lời giải

Phủ định của mệnh đề:

$“\exists x\in ℝ,x^2-x-6=0”$ 

là mệnh đề: $“\forall x\in ℝ,x^2-x-6\ne 0”$.

Câu 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Tích hai số thực trái dấu là một số thực âm.

b) Mọi số tự nhiên đều là dương.

c) Có sự sống ngoài Trái Đất

d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.

Câu 2: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.

a) A: “$\frac{5}{1,2}$ là một phân số".

b) B: "Phương trình $x^2+3x+2=0$ có nghiệm".

c) $C:"2^2+2^3=2^{2+3}"$.

d) D: “Số 2025 chia hết cho 15".

Câu 3: Cho n là số tự nhiên. Xét các mệnh đề:

P: “n là một số tự nhiên chia hết cho 16".

Q: "n là một số tự nhiên chia hết cho 8".

a) Phát biểu mệnh đề $P\Rightarrow Q$. Nhận xét tính đúng sai của mệnh đề đó.

b) Phát biểu mệnh đề đảo của mệnh đề $P\Rightarrow Q$. Nhận xét tính đúng sai của mệnh đề đó.

Câu 4: Cho tam giác ABC. Xét các mệnh đề:

P: “Tam giác ABC cân”.

Q: "Tam giác $ABC$ có hai đường cao bằng nhau".

Phát biểu mệnh đề $P\iff Q$ bằng bốn cách.

Câu 5: Dùng kí hiệu $"\forall$ hoặc $\exists$" để viết các mệnh đề sau:

a) Có một số nguyên không chia hết cho chính nó.

b) Mọi số thực cộng với 0 đều bằng chính nó.

Câu 6: Phát biểu các mệnh đề sau:

a) $\forall x\in ℝ,x^2\ge 0$

b) $\exists x\in ℝ,\frac{1}{x}>x$.

Câu 7: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó:

a) $\forall x\in ℝ,x^2\ne 2x-2$

b) $\forall x\in ℝ,x^2\le 2x-1$

c) $\exists x\in ℝ,x+\frac{1}{x}\ge 2$

d) $\exists x\in ℝ,x^2-x+1<0$

Câu 1. Trong các câu sau, câu nào là mệnh đề?

a) Trung Quốc là nước đông dân nhất thế giới;

b) Bạn học trường nào?

c) Không được làm việc riêng trong trường học;

d) Tôi sẽ sút bóng trúng xà ngang.

Câu 1.2. Xét tính đúng sai của các mệnh đề sau:

a) $\pi <\frac{10}{3}$;

b) Phương trình $3x+7=0$ có nghiệm;

c) Có ít nhất một số cộng với chính nó bằng 0;

d) 2022 là hợp số.

Câu 1.3. Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông”;

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”.

Hãy phát biểu mệnh đề tương $P\iff Q$đươngxét tính đúng sai của mệnh đề này.

Câu 1.4. Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng.

P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;

Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”.

Câu 1.5. Với hai số thực a và b, xét các mệnh đề $P:"a^2<b^2"$ và $Q:"0<a<b"$.

a) Hãy phát biểu mệnh đề $P\Rightarrow Q$.

b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.

c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.

Câu 1.6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “ $\exists n\in \mathbb{N}$, n chia hết cho n+1”.

Câu 1.7. Dùng kí hiệu $\forall ,\exists$ để viết các mệnh đề sau:

P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”;

Q: “ Có một số thực cộng với chính nó bằng 0”.

................................

................................

................................

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn lớp 10 - Cánh diều

BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bất phương trình bậc nhất hai ẩn $x,y$ là bất phương trình có một trong các dạng sau: $ax+by\le c;$$ax+by<c;ax+by\ge c;ax+by>c$

trong đó $a,b,c$ là những số thực đã cho, $a$ và $b$ không đồng thời bằng $0,x$ và $y$ là các ẩn số.

Cho bất phương trình bậc nhất hai ẩn $x,y$: $ax+by<c\left(1\right)$. Mỗi cặp số $\left(x_0;y_0\right)$ sao cho $a{x}_0+b{y}_0<c$ là mệnh đề đúng được gọi là một nghiệm của bất phương trình (1). Trong mặt phẳng tọa độ $Oxy$, tập hợp tất cả các điểm có tọa độ thỏa mãn bất phương trình (1) được gọi là miền nghiệm của bất phương trình (1).

II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ $Oxy$ tập hợp các điểm có tọa độ là nghiệm của bất phương trình được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình $ax+by\le c$ như sau (tương tự cho bất phương trình $ax+by\ge c$)

- Bước 1. Trên mặt phẳng tọa độ $Oxy,$ vẽ đường thẳng $\Delta :ax+by=c.$

- Bước 2. Lấy một điểm $M_0\left(x_0;y_0\right)$ không thuộc $\Delta$ (ta thường lấy gốc tọa độ $O$)

- Bước 3. Tính $a{x}_0+b{y}_0$ và so sánh $a{x}_0+b{y}_0$ với $c$

- Bước 4. Kết luận

Nếu $a{x}_0+b{y}_0<c$ thì nửa mặt phẳng bờ $\Delta$ chứa $M$ là miền nghiệm của $a{x}_0+b{y}_0\le c.$

Nếu $a{x}_0+b{y}_0>c$ thì nửa mặt phẳng bờ $\Delta$ không chứa $M$ là miền nghiệm của $a{x}_0+b{y}_0\le c.$

Chú ý:

Miền nghiệm của bất phương trình $a{x}_0+b{y}_0\le c$ bỏ đi đường thẳng $ax+by=c$ là miền nghiệm của bất phương trình $a{x}_0+b{y}_0<c.$

Câu 1: Cặp số nào sau đây là nghiệm của bất phương trình $2x-3y<3$?

a) $(0;-1)$

b) $(2;1)$

c) $(3;1)$

Câu 2: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $x+2y<3$

b) $3x-4y\ge -3$

c) $y\ge -2x+4$

d) $y<1-2x$

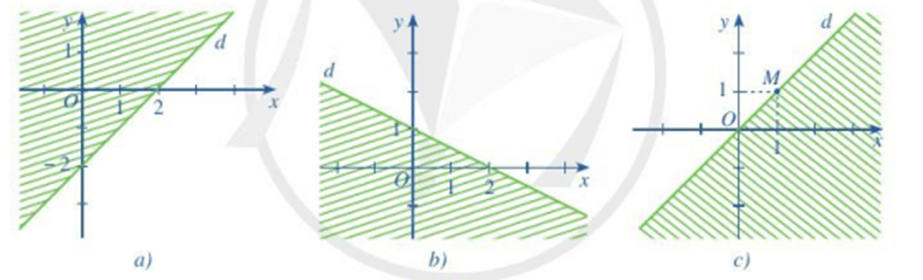
Câu 3:Phần không gạch (không kể d) ở mỗi Hình a, b, c là miền nghiệm của bất phương trình nào?

Câu 4:Một gian hàng trưng bày bàn và ghế rộng $60m^2$. Diện tích để kê một chiếc ghế là $0,5m^2$, một chiếc bàn là $1,2m^2$. Gọi x là số chiếc ghế, y là số chiếc bàn được kê.

a) Viết bất phương trình bậc nhất hai ẩn $x,y$ cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là $12m^2$

b) Chỉ ra ba nghiệm của bất phương trình trên.

Câu 5:Trong 1 lạng (100 g thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46g protein. (Nguồn:https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn $x,y$ để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) $2x+3y>6$;

b) $2^{2}x+y\le 0$;

c) $2x^2-y\ge 1$.
Câu 2. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng toạ độ:
a) $3x+2y\ge 300$;

b) $7x+20y<0$.

Câu 3. Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

	Phí cố định (nghìn đồng/ngày)	Phí tính theo quãng đường di chuyển (nghìn đồng/kilômét)
Từ thứ Hai đến thứ Sáu	900	8
Thứ Bảy và Chủ nhật	1500	10

a) Gọi $x$ và $y$ lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa $x$ và $y$ sao cho tổng số tiền ông An phải trả không quá $14$ triệu đồng.

b) Biểu diển miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ.

BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn $x,y$ mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau:

- Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

- Phần không bị gạch là miền nghiệm cần tìm.

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính.

Câu 1:Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.

Câu 2:Biểu diễn miền nghiệm của hệ bất phương trình:

Câu 3:Miền không bị gạch ở mỗi Hình $12a,12b$ là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

12a)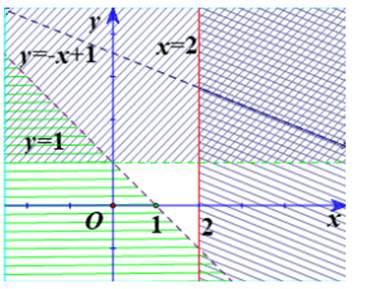

12b)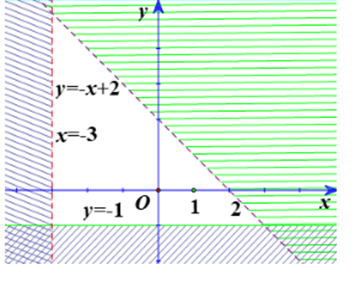

Câu 4:Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.

Câu 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

Câu 2. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

Câu 3. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

................................

................................

................................

Trên đây tóm tắt nội dung có trong Chuyên đề dạy thêm Toán 10 Cánh diều, để mua tài liệu mời Thầy/Cô xem thử:

Xem thử

Lời giải bài tập lớp 10 sách mới:

• Giải bài tập Lớp 10 Kết nối tri thức
• Giải bài tập Lớp 10 Chân trời sáng tạo
• Giải bài tập Lớp 10 Cánh diều

---