Cách giải bài toán đếm hình sử dụng Tổ hợp (cực hay có lời giải)
Bài viết Cách giải bài toán đếm hình sử dụng Tổ hợp với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách giải bài toán đếm hình sử dụng Tổ hợp.
Cách giải bài toán đếm hình sử dụng Tổ hợp (cực hay có lời giải)
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
A. Phương pháp giải
Định nghĩa : Cho tập hợp X có n phần tử (n≥1) và số nguyên k với 1≤k≤n. Mỗi tập con gồm k phần tử của X gọi là một tổ hợp chập k của n phần tử đã cho (gọi tắt là một tổ hợp chập k của X).
Công thức : Số các tổ hợp chập k của tập hợp có n phần tử được kí hiệu là 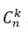
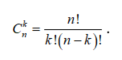
+ Một đường thẳng được xác định nếu biết hai điểm phân biệt thuộc đường thẳng đó.
+ Ba điểm không thẳng hàng tạo thành một tam giác.
+ Trong một đường tròn; dây cung đi qua tâm gọi là đường kính.
+ Dấu hiệu nhận biết hình chữ nhật: tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình chữ nhật .
+ Dấu hiệu nhận biết hình bình hành: tứ giác có các cạnh đối song song với nhau là hình bình hành.
B. Ví dụ minh họa
Ví dụ 1: Số tam giác xác định bởi các đỉnh của một đa giác lồi 16 cạnh.
A.560 B.420 C.240 D.280
Hướng dẫn giải :
Đáp án : A
Đa giác lồi đã cho có 16 cạnh nên đa giác này có 16 đỉnh.
Một tam giác được xác định nếu biết ba đỉnh của nó.
Do đó số tam giác xác định bởi các đỉnh của đa giác lồi đã cho là: 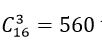
Ví dụ 2: Cho một đa giác có 12 cạnh. Hỏi đa giác này có bao nhiêu đường chéo.
A.48 B.51 C.54 D.62
Hướng dẫn giải :
Đáp án : C
Đa giác đã cho có 12 cạnh nên có 12 đỉnh.
Số đoạn thẳng được tạo ra từ 12 đỉnh này là: 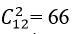
Mà đa giác này có 12 cạnh nên đa giác này có số đường chéo là: 66- 12= 54 đường chéo.
Chú ý: Số cạnh+ số đường chéo =số đoạn thẳng nối 2 đỉnh bất kì.
Ví dụ 3: Cho đa giác lồi n đỉnh (n≥4) . Hỏi đa giác đã cho có bao nhiêu đường chéo?

Hướng dẫn giải :
Đáp án : C
Do đa giác này có n đỉnh nên đa giác này có n cạnh.
Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là:
⇒ Số đường chéo của đa giác là:
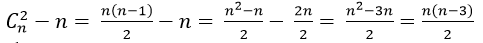
Ví dụ 4: Cho một đa giác có n đỉnh. Biết rằng đa giác này có 20 đường chéo. Tìm n?
A.7 B.8 C.10 D.12
Hướng dẫn giải :
Đáp án : B
+ Do đa giác này có n đỉnh nên đa giác này có n cạnh .
+ Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là:
⇒ Số đường chéo của đa giác là:
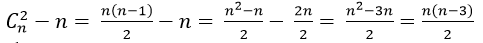
+ Theo giả thiết ta có: (n(n-3))/2=20
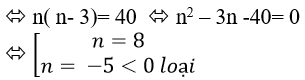
Vậy đa giác đã cho có 8 đỉnh.
Ví dụ 5: Số giao điểm tối đa của 12 đường thẳng phân biệt là:
A.66 B.132 C.120 D.45
Hướng dẫn giải :
Đáp án : A
Hai đường thẳng phân biệt có tối đa 1 giao điểm.
⇒ số giao điểm tối đa của 12 đường thẳng là: 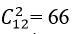
Ví dụ 6: Cho một đường tròn và 5 đường thẳng phân biệt. Hỏi có tối đa bao nhiêu giao điểm?
A.10 B.15 C. 20 D. 25
Hướng dẫn giải :
Đáp án : C
+ Ta tính số giao điểm tối đa của 5 đường thẳng:
Hai đường thẳng phân biệt có tối đa 1 giao điểm
⇒ số giao điểm tối đa của 5 đường thẳng là: 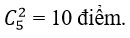
+ Ta tính số giao điểm tối đa của 5 đường thẳng với đường tròn.
Một đường thẳng cắt đường tròn tối đa tại hai điểm
⇒ 5 đường thẳng cắt đường tròn tối đa: 2.5= 10 điểm
⇒ Số giao điểm tối đa của 5 đường thẳng và đường tròn là:10 + 10= 20 điểm
Ví dụ 7: Cho hai đường thẳng song song a và b. Trên đường thẳng a cho 6 điểm phân biệt, trên đường thẳng b cho 7 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh là các điểm đã cho trên hai đường a và b.
A.364 B.231 C.288 D.210
Hướng dẫn giải :
Đáp án : B
- Trường hợp 1. Tam giác có 2 đỉnh nằm trên a và 1 đỉnh thuộc b
+ Có 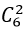
+ Có 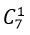
+ Theo quy tắc nhân có : 15.7= 105 tam giác.
- Trường hợp 2. Tam giác có 1 đỉnh nằm trên a và 2 đỉnh thuộc b
+ Có 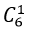
+ Có 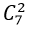
+ Theo quy tắc nhân có : 6.21= 126 tam giác.
Kết hợp hai trường hợp ta có : 105 + 126= 231 tam giác
Ví dụ 8: Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt ( n>1). Biết có 2800 tam giác có đỉnh là các điểm nói trên.Tìm n?
A.20 B.21 C.30 D.32
Hướng dẫn giải :
Đáp án : A
- Trường hợp 1. Tam giác có 2 đỉnh nằm trên d1 và 1 đỉnh thuộc d2
+ Có 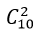
+ Có 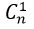
+ Theo quy tắc nhân có : 45.n tam giác.
- Trường hợp 2. Tam giác có 1 đỉnh nằm trên d1 và 2 đỉnh thuộc d2
+ Có 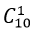
+ Có 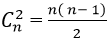
+ Theo quy tắc nhân có :
Do đó số tam giác được tạo ra là : 45n+5n( n-1)
Theo đề bài ta có : 45n + 5n( n-1)= 2800
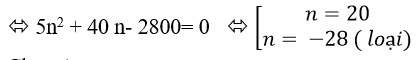
Ví dụ 9: Cho đa giác đều A1A2....A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1 ;A2 ;.... ; A2n gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1 ;A2 ;.... ; A2n. Tìm n?
A.3 B.6 C.8 D.12
Hướng dẫn giải :
Đáp án : C
+ Số tam giác có đỉnh là 3 trong số 2n điểm đã cho là:
+ Do đa giác đều A1A2....A2n nội tiếp trong đường tròn tâm O nên các đoạn thẳng A1An+1; A2An+ 2;...; AnA2n là n đường kính .
+ Số các hình chữ nhật có đỉnh là 4 trong 2n điểm A1 ;A2 ;.... ; A2n là
( Cứ hai đường kính cho ta một hình chữ nhật nên số các hình chữ nhật thỏa mãn chính bằng số cách chọn 2 đường kính trong n đường kính).
+ Theo đầu bài ta có phương trình :
Vậy n= 8.
Ví dụ 10: Cho 10 đường thẳng song song lần lượt cắt 8 đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng trên.
A.45 B.28 C.73 D.1260
Hướng dẫn giải :
Đáp án : D
Ta chia các đường thẳng đã cho thành 2 nhóm:
+ Nhóm 1: là 10 đường thẳng song song với nhau
+ Nhóm 2: Là 8 đường thẳng song song với nhau
Tứ giác có các cạnh đối diện song song với nhau là hình bình hành.
+ Bước 1: Chọn 2 đường thẳng nhóm 1 có:
+ Bước 2: Chọn 2 đường thẳng nhóm 2 có:
Số hình bình hành được tạo ra là; 45.28= 1260 hình
Ví dụ 11: Trong mặt phẳng tọa độ cho đa giác (H): A1A2...A10. Hỏi từ các đỉnh của đa giác (H) ta lập được bao nhiêu tam giác có đúng 1 cạnh của (H)?
A.54 B.64 C.60 D.72
Hướng dẫn giải :
Đáp án : C
Đa giác A1A2..A10 là đa giác có 10 đỉnh và có 10 cạnh .
Giả sử tam giác AiAjAk ( 1≤i,j,k≤10) có đúng 1 cạnh của ( H).
Giả sử AiAj là một cạnh của ( H). Khi đó số cách chọn cạnh này là: 10( vì đa giác (H) có 10 cạnh).
Số cách chọn đỉnh còn lại Ak là 6 cách ( đỉnh này khác Ai; Aj và khác hai đỉnh liền kề với Ai,Aj )
Theo quy tắc nhân; số tam giác thỏa mãn là 10.6= 60 tam giác.
Ví dụ 12: Trong mặt phẳng cho đa giác đều (H) có 20 cạnh. Có bao nhiêu tam giác có 3 đỉnh là các đỉnh của (H) nhưng không có cạnh nào là cạnh của (H) ?
A.4760 B.3720 C.3600 D.2400
Hướng dẫn giải :
Đáp án : A
Do đa giác đã cho có 20 cạnh nên đa giác này có 20 đỉnh là A1; A2; ..; A20.
+ Bước 1. Chọn đỉnh thứ nhất Ai: có 20 cách.
+ Bước 2. Chọn đỉnh thứ hai Aj: đỉnh thứ 2 khác đỉnh thứ nhất và khác với đỉnh liền kề với Ai ( chú ý tam giác cần lập không có cạnh nào của ( H)) nên có 17 cách chọn đỉnh Aj
+ Bước 3. Chọn đỉnh thứ ba Ak: khác đỉnh thứ nhất - thứ hai; khác 2 đỉnh liền kề Ai; khác 2 đỉnh liền kề Aj nên có 14 cách chọn Ak.
Theo quy tắc nhân có: 20.17.14= 4760 tam giác thỏa mãn.
C. Bài tập trắc nghiệm
Câu 1: Số tam giác xác định bởi các đỉnh của một đa giác lồi có 13 đỉnh.
A.128 B.143 C.286 D.426
Lời giải:
Đáp án : C
Một tam giác được xác định nếu biết ba đỉnh của nó.
Do đó; số tam giác xác định bởi các đỉnh của đa giác lồi đã cho là:
Câu 2: Một đa giác (H) có n cạnh. Biết rằng từ n đỉnh của đa giác ta lập được 816 tam giác. Tìm n?
A.18 B.17 C.16 D.14
Lời giải:
Đáp án : A
Do đa giác (H) có n cạnh nên đa giác này có n đỉnh .
Một tam giác được xác định nếu biết ba đỉnh của tam giác đó.
Do đó; từ n đỉnh của đa giác ta lập được số tam giác là:
Theo giả thiết ta có:
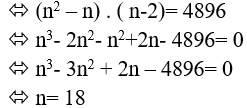
Câu 3: Cho một đa giác có 14 cạnh. Hỏi đa giác này có bao nhiêu đường chéo.
A.72 B.68 C.54 D.77
Lời giải:
Đáp án : D
Đa giác đã cho có 14 cạnh nên có 14 đỉnh.
Số đoạn thẳng được tạo ra từ 14 đỉnh này là: 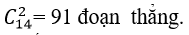
Mà đa giác này có 14 cạnh nên đa giác này có số đường chéo là:
91- 14= 77 đường chéo
Chú ý: Số cạnh+ số đường chéo =số đoạn thẳng nối 2 đỉnh bất kì.
Câu 4: Cho một đa giác có n đỉnh. Biết rằng đa giác này có 35 đường chéo. Tìm n?
A.7 B.8 C.10 D.12
Lời giải:
Đáp án : C
Do đa giác này có n đỉnh nên đa giác này có n cạnh.
Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là:
⇒ Số đường chéo của đa giác là:
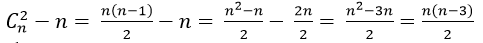
Theo giả thiết ta có:
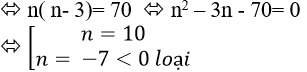
Vậy đa giác đã cho có 10 đỉnh
Câu 5: Số giao điểm tối đa của 18 đường thẳng phân biệt là:
A.306 B.324 C.153 D.174
Lời giải:
Đáp án :
Hai đường thẳng phân biệt có tối đa 1 giao điểm.
⇒ Số giao điểm tối đa của 18 đường thẳng là:
Câu 6: Cho một đường tròn và 7 đường thẳng phân biệt. Hỏi có tối đa bao nhiêu giao điểm ?
A.28 B.14 C.21 D.35
Lời giải:
Đáp án : D
+ Ta tính số giao điểm tối đa của 7 đường thẳng với nhau:
Hai đường thẳng phân biệt có tối đa 1 giao điểm
⇒ số giao điểm tối đa của 7 đường thẳng là:
+ Ta tính số giao điểm tối đa của 7 đường thẳng với đường tròn.
Một đường thẳng cắt đường tròn tối đa tại hai điểm
⇒ 7 đường thẳng cắt đường tròn tối đa: 2.7= 14 điểm
⇒ Số giao điểm tối đa của 5 đường thẳng và đường tròn là: 21+ 14= 35 điểm
Câu 7: Cho hai đường thẳng song song a và b. Trên đường thẳng a cho 8 điểm phân biệt, trên đường thẳng b cho 6 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh là các điểm đã cho trên hai đường a và b.
A.364 B.231 C.288 D.210
Lời giải:
Đáp án : C
- Trường hợp 1. Tam giác có 2 đỉnh nằm trên a và 1 đỉnh thuộc b
+ Có 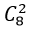
+ Có 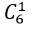
Theo quy tắc nhân có : 28. 6= 168 tam giác.
- Trường hợp 2. Tam giác có 1 đỉnh nằm trên a và 2 đỉnh thuộc b
+ Có 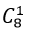
+ Có 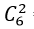
Theo quy tắc nhân có : 8. 15= 120 tam giác.
Kết hợp hai trường hợp ta có : 168 + 120= 288 tam giác.
Câu 8: Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 9 điểm phân biệt, trên d2 có n điểm phân biệt ( n>1). Biết có 540 tam giác có đỉnh là các điểm nói trên.Tìm n?
Lời giải:
Đáp án : C
- Trường hợp 1. Tam giác có 2 đỉnh nằm trên d1 và 1 đỉnh thuộc d2
+ Có 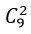
+ Có 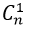
Theo quy tắc nhân có : 36.n tam giác.
- Trường hợp 2. Tam giác có 1 đỉnh nằm trên d1 và 2 đỉnh thuộc d2
+ Có 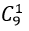
+ Có 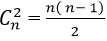
Theo quy tắc nhân có :
Do đó ; số tam giác được tạo ra là :
Theo đề bài ta có : 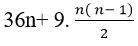
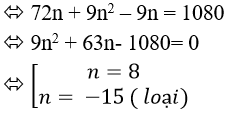
Câu 9: Cho đa giác đều A1A2....A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1 ;A2 ;.... ; A2n gấp 76/3 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1 ;A2 ;.... ; A2n. Tìm n?
A.10 B.9 C.8 D.15
Lời giải:
Đáp án :
+ Số tam giác có đỉnh là 3 trong số 2n điểm đã cho là:
+ Do đa giác đều A1A2....A2n nội tiếp trong đường tròn tâm O nên các đoạn thẳng A1An+1; A2An+ 2;...; AnA2n là n đường kính .
+ Số các hình chữ nhật có đỉnh là 4 trong 2n điểm A1 ;A2 ;.... ; A2n là
( Cứ hai đường kính cho ta một hình chữ nhật nên số các hình chữ nhật thỏa mãn chính bằng số cách chọn 2 đường kính trong n đường kính).
+ Theo đầu bài ta có phương trình :
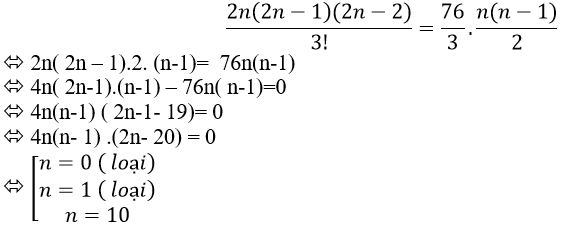
Câu 10: Cho15 đường thẳng song song lần lượt cắt 12 đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng trên.
A.6290 B.6930 C.1440 D.5260
Lời giải:
Đáp án : B
Ta chia các đường thẳng đã cho thành 2 nhóm:
+ Nhóm 1: là 15 đường thẳng song song với nhau
+ Nhóm 2: là 10 đường thẳng song song với nhau
Tứ giác có các cạnh đối diện song song với nhau là hình bình hành.
+ Bước 1. Chọn 2 đường thẳng nhóm 1 có:
+ Bước 2. Chọn 2 đường thẳng nhóm 2 có:
Số hình bình hành được tạo ra là : 105. 66 = 6930 hình
Câu 11: Cho 5 đường tròn phân biệt và 4 đường thẳng phân biệt.Hỏi có tối đa bao nhiêu giao điểm giữa các đường tròn và đường thẳng?
A.66 B.34 C.60 D.Đáp án khác
Lời giải:
Đáp án : A
+ Bước 1. Ta tính số giao điểm tối đa của 5 đường tròn:
Hai đường tròn phân biệt có tối đa 2 điểm chung. Nên số giao điểm tối đa của 5 đường tròn là :
+ Bước 2. Ta tính số giao điểm tối đa của 4 đường thẳng:
Hai đường thẳng phân biệt có tối đa 1 điểm chung nên số giao điểm tối đa của 4 đường thẳng này là :
+ Bước 3. Số giao điểm tối đa của các đường tròn với các đường thẳng :
Một đường thẳng cắt đưởng tròn tối đa tại hai điểm.
⇒ 4 đường thẳng cắt 1 đường tròn tối đa tại: 4.2= 8 điểm
⇒ 4 đường thẳng cắt 5 đường tròn tối đa tại: 8.5= 40 điểm
Do đó; số giao điểm tối đa giữa các đường thẳng và đường tròn là : 20 + 6 + 40= 66 điểm
Câu 12: Trong mặt phẳng tọa độ cho đa giác (H): A1A2...A16. Hỏi từ các đỉnh của đa giác (H) ta lập được bao nhiêu tam giác có đúng 1 cạnh của (H)?
Lời giải:
Đáp án : B
Đa giác A1A2...A16 là đa giác có 16 đỉnh và có 16 cạnh .
Giả sử tam giác AiAjAk ( 1≤i,j,k≤16) có đúng 1 cạnh của ( H).
Giả sử AiAj là một cạnh của ( H). Khi đó số cách chọn cạnh này là: 16 ( vì đa giác (H) có 16 cạnh).
Số cách chọn đỉnh còn lại Ak là 12 cách ( đỉnh này khác Ai; Aj và khác hai đỉnh liền kề với Ai,Aj )
Theo quy tắc nhân; số tam giác thỏa mãn là 16.12 = 192 tam giác.
Câu 13: Trong mặt phẳng cho đa giác đều (H) có 15 cạnh. Có bao nhiêu tam giác có 3 đỉnh là các đỉnh của (H) nhưng không có cạnh nào là cạnh của (H) ?
A.2760 B.1720 C.1600 D.1620
Lời giải:
Đáp án : D
Do đa giác đã cho có 15 cạnh nên đa giác này có 15 đỉnh là A1; A2; ..; A15.
+ Bước 1. Chọn đỉnh thứ nhất Ai: có 15 cách.
+ Bước 2. Chọn đỉnh thứ hai Aj: đỉnh thứ 2 khác đỉnh thứ nhất và khác với đỉnh liền kề với Ai ( chú ý tam giác cần lập không có cạnh nào của ( H)) nên có 12 cách chọn đỉnh Aj
+ Bước 3. Chọn đỉnh thứ ba Ak: khác đỉnh thứ nhất - thứ hai; khác 2 đỉnh liền kề Ai; khác 2 đỉnh liền kề Aj nên có 9 cách chọn Ak.
Theo quy tắc nhân có: 15.12.9= 1620 tam giác thỏa mãn.
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
- Cách giải bài toán đếm số sử dụng Tổ hợp (cực hay có lời giải)
- Cách khai triển nhị thức Newton: tìm hệ số, số hạng trong khai triển cực hay
- Tìm số hạng chứa x^a trong khai triển đa thức P (cực hay có lời giải)
- Cách tìm hệ số lớn nhất trong khai triển (cực hay có lời giải)
- Bài tập về nhị thức Newton nâng cao (cực hay có lời giải)
- Cách xác định phép thử, không gian mẫu (cực hay có lời giải)
- Cách tìm xác suất của biến cố (cực hay có lời giải)
- Cách tính xác suất bài toán liên quan đến đếm số (cực hay có lời giải)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều

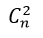
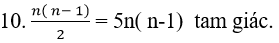
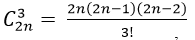
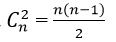
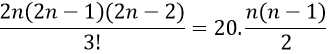
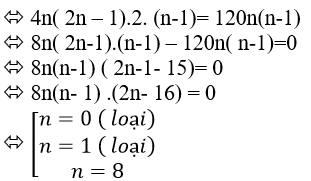
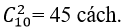
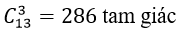
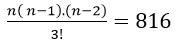
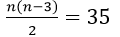
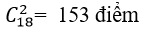
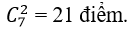
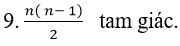
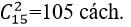
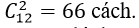
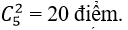
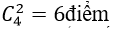



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

