Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)
Bài viết Phương pháp giải bài tập Tổ hợp với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Phương pháp giải bài tập Tổ hợp.
Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
A. Phương pháp giải
Định nghĩa :
Cho tập hợp X có n phần tử (n≥1) và số nguyên k với 1≤k≤n. Mỗi tập con gồm k phần tử của X gọi là một tổ hợp chập k của n phần tử đã cho (gọi tắt là một tổ hợp chập k của X).
Số các tổ hợp chập k của tập hợp có n phần tử được kí hiệu là 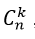
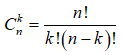
Chú ý :
- Ta quy ước tổ hợp chập 0 của n phần tử là tập rỗng, như vậy 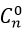
- Số các chỉnh hợp chập k của n phần tử nhiều hơn k! lần số các tổ hợp chập k của n phần tử
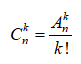
Từ các bài toán trên ta rút ra được quy luật phân biệt tổ hợp và chỉnh hợp như sau:
- Chỉnh hợp và tổ hợp liên hệ với nhau bởi công thức: 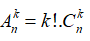
- Chỉnh hợp: Có thứ tự.
- Tổ hợp: Không có thứ tự.
- Những bài toán mà kết quả phụ thuộc vào vị trí các phần tử thì sử dụng chỉnh hợp. Ngược lại thì sử dụng tổ hợp.
- Cách lấy k phần tử từ tập n phần tử (k≤n) :
+ Không thứ tự : 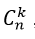
+ Có thứ tự :
B. Ví dụ minh họa
Ví dụ 1 : Có 15 tay đua xe đạp cùng xuất phát trong một cuộc đua để chọn ra 3 người về đích đầu tiên. Số kết quả có thể xảy ra là:
A.455 B.910 C.2730 D.2400
Hướng dẫn giải :
Đáp án : A
Cần chọn ra 3 người về đích đầu tiên, nên giữa 3 người này không cần phải phân định thứ tự nhất nhì ba.
Số kết quả xảy ra là:
Ví dụ 2 : Từ một nhóm gồm 6 nam và 5 nữ cần chọn ra 4 người trong đó có ít nhất một nữ. Hỏi có bao nhiêu cách chọn như vậy ?
A.75 B.330 C.315 D.325
Hướng dẫn giải :
Đáp án : C
+ Số cách chọn ra 4 người bất kì từ 11 người là: 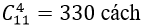
+ Số cách chọn ra 4 nam trong 6 nam là:
⇒ số cách chọn ra 4 người trong đó có ít nhất 1 nữ là: 330- 15= 315 cách
Ví dụ 3 : Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
A.60 B.180 C.300 D.90
Hướng dẫn giải :
Đáp án : A
Chọn 3 học sinh lớp 12 có
Chọn 1 học sinh lớp 11 có
Chọn 1 học sinh lớp 10 có
Do đó có; 4.3.5= 60 cách chọn
Ví dụ 4 : Hai đơn vị thi đấu cờ tướng A và B lần lượt có 5 người và 6 người. Cần chọn ra mỗi đơn vị 3 người để ghép cặp thi đấu với nhau. Hỏi có bao nhiêu cách thực hiện như thế?
A.1500 B.1600 C.1200 D.1540
Hướng dẫn giải :
Đáp án : C
+ Số cách chọn 3 người từ đơn vị A là
+ Số cách chọn 3 người từ đơn vị B là
+ Sau khi chọn 3 người từ mỗi đơn vị; ta đi ghép các cặp đấu.
Đánh số thứ tự của 3 người từ đơn vị A lần lượt là 1; 2; 3.
Người thứ 1 của đơn vị B có 3 cách chọn; người thứ 2 của đơn vị B có 2 cách chọn và người thứ 3 của đơn vị B có 1 cách chọn.
⇒ Có 3.2.1= 6 cách ghép các cặp đấu.
Vậy có: 10 .20. 6= 1200 cách thực hiện việc ghép cặp thi đấu.
Ví dụ 5 : Cho 2 đường thẳng a và b song song với nhau.Trên đường thẳng a lấy 7 điểm phân biệt, trên đường thẳng b lấy 6 điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ 13 điểm đã cho?
A.240 B.231 C.210 D.180
Hướng dẫn giải :
Đáp án : B
Số tam giác có 1 đỉnh nằm trên a và 2 đỉnh nằm trên b là:
Số tam giác có 2 đỉnh nằm trên a và 1 đỉnh nằm trên b là:
Do đó số tam giác có thể dựng được là : 105+ 126 = 231 tam giác
Ví dụ 6 : Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?
A.240 B.180 C.126 D.120
Hướng dẫn giải :
Đáp án : D
Số cách chọn ban quản trị gồm 1 nam và 3 nữ là
Số cách chọn ban quản trị gồm 2 nam và 2 nữ là
Số cách chọn ban quản trị gồm 3 nam và 1 nữ là
Vậy tổng số cách chọn cần tìm là: 20+ 60+ 40= 120 cách.
Ví dụ 7 : Bạn Hồng có 15 bông hoa. Trong đó; có 5 bông hoa hồng; 4 bông hoa ly và 6 bông hoa lan. Hỏi bạn Hồng có bao nhiêu cách chọn ra 3 bông hoa hồng; 3 bông hoa ly và 4 bông hoa lan?
A.240 B.300 C.540 D.600
Hướng dẫn giải :
Đáp án : D
+ Số cách chọn ra 3 bông hoa hồng từ 5 bông hoa hồng là:
+ Số cách chọn ra 3 bông hoa ly từ 4 bông hoa ly là :
+ Số cách chọn ra 4 bông hoa lan từ 6 bông hoa lan là:
⇒ Số cách chọn thỏa mãn đầu bài là: 10 .4. 15= 600 cách.
Ví dụ 8 : Có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình, 15 câu dễ. Từ 30 câu đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu khác nhau, sao cho mỗi đề phải có 3loại câu hỏi (khó, trung bình, dễ) và số câu dễ không ít hơn 2?
A.56875 B.58765 C.87625 D.22575
Hướng dẫn giải :
Đáp án : A
Trường hợp 1: Đề gồm 2 câu dễ, 2 câu khó, 1 câu trung bình thì có
Trường hợp 2: Đề gồm 2 câu dễ, 1 câu khó và 2 câu trung bình thì có
Trường hợp 3: Đề gồm 3 câu dễ, 1 câu khó và 1 câu trung bình thì có
Theo quy tắc cộng thì có 10500 + 23625 + 22750 = 56875 đề.
Ví dụ 9 : Một hộp bi có 5 viên bi đỏ, 5 viên bi vàng và 3viên bi xanh. Có bao nhiêu cách để lấy 4 viên bi từ hộp sao cho trong 4 viên bi lấy được số bi đỏ lớn hơn số bi vàng; biết rằng trong 4 viên bi lấy ra có bi màu xanh
A.180 B.150 C.210 D.270
Hướng dẫn giải :
Đáp án : C
Trường hợp 1 : 4 bi lấy ra có: 3 đỏ; 1 xanh và 0 vàng:
Trường hợp 2 : 4 bi lấy ra có 2 đỏ; 1 xanh và 1 vàng:
Trường hợp 3 : 4 bi lấy ra có: 2 đỏ, 2 xanh và 0 vàng:
⇒ Số cách lấy thỏa mãn là: 30+ 150+ 30= 210 cách.
Ví dụ 10 : Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
A.120 B.150 C.240 D.255
Hướng dẫn giải :
Đáp án : D
Số cách chọn 4 học sinh bất kì từ 12 học sinh là 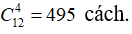
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau:
Trường hợp 1 : Lớp A có hai học sinh, các lớp B; C mỗi lớp có 1 học sinh:
Chọn 2 học sinh trong 5 học sinh lớp A có
Chọn 1 học sinh trong 4 học sinh lớp B có
Chọn 1 học sinh trong 3 học sinh lớp C có
Suy ra số cách chọn là
Trường hợp 2 : Lớp B có 2 học sinh, các lớp A, C mỗi lớp có 1 học sinh:
Tương tự ta có số cách chọn là
Trường hợp 3 : Lớp C có 2 học sinh, các lớp A, B mỗi lớp có 1 học sinh:
Tương tự ta có số cách chọn là
Vậy số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là: 120 + 90 + 60 = 270 cách.
Số cách chọn ra 4 học sinh thuộc không quá 2 trong 3 lớp trên là: 495 – 270= 225 cách.
Ví dụ 11 : Từ 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa xem như đôi một khác nhau), người ta muốn chọn một bó hồng gồm 7 bông, hỏi có bao nhiêu cách chọn bó hoa trong đó có ít nhất 3 bông hồng vàng và 3 bông hồng đỏ?
A.200 cách B.210 cách C. 120 cách D. 150cách
Hướng dẫn giải :
Đáp án : D
Ta thấy do chỉ chọn 7 bông hồng mà có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ nên chỉ có 3 trường hợp sau:
Trường hợp 1 : Chọn được 3 bông hồng vàng và 4 bông hồng đỏ.
Số cách chọn 3 bông hồng vàng là
Số cách chọn 4 bông hồng đỏ là
Theo quy tắc nhân thì có
Trường hợp 2 : Chọn được 4 bông hồng vàng và 3 bông hồng đỏ.
Tương tự TH1 thì ta có
Trường hợp 3 : Chọn được 3 bông hồng vàng, 3 bông hồng đỏ và 1 bông hồng trắng.
Tương tự thì có
Vậy theo quy tắc cộng thì có: 10+ 20+ 120 = 150 cách.
C. Bài tập trắc nghiệm
Câu 1: Lớp 10 A2 có 20 học sinh nữ và 18 học sinh nam. Hỏi cô giáo chủ nhiệm có bao nhiêu cách chọn ra 3 bạn đi trực nhật.
A.8436 B.7654 C.6548 D.5448
Lời giải:
Đáp án : A
Lớp 10A2 có tất cả 20 + 18= 38 học sinh.
Số cách chọn ra 3 bạn từ 38 bạn là:
Câu 2: Từ 15 người, Đảng ủy thành lập một ban kiểm tra gồm 1 người lãnh đạo và 3 ủy viên. Hỏi có bao nhiêu cách thành lập ban kiểm tra?
A.1820 B.32760 C.5460 D.10540
Lời giải:
Đáp án : C
Số cách chọn 1 lãnh đạo từ 15 người đã cho:
Số cách chọn 3 ủy viên từ 14 người còn lại:
Tổng số cách thành lập ban kiểm tra là: 15. 364= 5460 cách.
Câu 3: Trong một bình đựng 6 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu?
A.18 B.9 C.22 D.25
Lời giải:
Đáp án : D
Số cách lấy hai viên bi cùng màu đỏ là
Số cách lấy hai viên bi cùng màu xanh là
Như vậy số cách lấy đươc hai viên bi cùng màu là: 15 + 10= 25 cách.
Câu 4: Tổ 1 của lớp 11A1 có 10 học sinh; tổ 2 có 11 học sinh; tổ 3 có 11 học sinh và tổ 4 có 10 học sinh. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn ra 1 bạn lớp trưởng và 4 bạn tổ trưởng.
A.4253340 B.101270 C.2430480 D.Đáp án khác
Lời giải:
Đáp án : A
+ Lớp 11A1 có tất cả: 10+ 11+ 11+ 10= 42 học sinh.
+ Có 42 cách chọn một bạn làm lớp trưởng.
+ Có 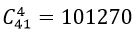
⇒ Số cách chọn 1 bạn lớp trưởng và 4 bạn làm tổ trưởng là: 42 .101270= 4253340 cách.
Câu 5: Mạnh có 7 người bạn thân trong đó có hai bạn Hùng và Tùng. Mạnh muốn mời 3 trong 7 người bạn đó về quê chơi vào cuối tuần. Số cách mời ba bạn về quê Mạnh chơi sao cho nếu có Hùng thì không có Tùng; nếu có Tùng thì không có Hùng là?
A.20 B.25 C.30 D.40
Lời giải:
Đáp án : C
Trường hợp 1 : Trong 3 bạn được mời, có Hùng nhưng không có Tùng.
Số cách chọn hai bạn còn lại đi cùng Hùng là:
Trường hợp 2 : có Tùng nhưng không có Hùng
Số cách chọn hai bạn còn lại là:
Trường hợp 3 : Trong 3 bạn được mời, không có cả Hùng và Tùng
Số cách chọn nhóm 3 người trong trường hợp này là
Vậy số cách chọn cần tìm là 10 + 10 + 10= 30 cách.
Câu 6: Bạn Mạnh có 10 bông hoa hồng; 8 bông hoa lan và 6 bông hoa huệ. Mạnh muốn chọn ra 6 bông để tặng Hương. Biết rằng số hoa hồng bằng số hoa lan.
A.24681 B.26821 C.18641 D.20241
Lời giải:
Đáp án : B
Trường hợp 1 : Tặng 6 bông hoa huệ: có 1 cách.
Trường hợp 2 : Tặng 1 hoa hồng; 1 hoa lan và 4 hoa huệ:
Trường hợp 3 : Tặng 2 hoa hồng; 2 hoa lan và 2 hoa huệ có:
Trường hợp 4 : Tặng 3 hoa hồng; 3 hoa lan có:
⇒ Số cách tặng thỏa mãn là: 1 + 1200 + 18900 + 6720 = 26821 cách.
Câu 7: Một lớp có 40 học sinh gồm 18 học sinh nam, 22 học sinh nữ, cần chọn ra 5 học sinh gồm cả nam và nữ đi trực tuần. Hỏi có bao nhiêu cách chọn để trong đó có ít nhất 3 nữ?
A.538950 B.905760 C.367290 D.144000
Lời giải:
Đáp án : C
Trường hợp 1: Chọn 3 nữ, 2 nam có
Trường hợp 2: Chọn 4 nữ, 1 nam có
Do đó có :
Câu 8: Công ty A có 6 nam và 5 nữ được xét tuyển vào ban quản trị. Hỏi có bao nhiêu cách lập ra ban quản trị có 5 người; trong đó có ít nhất 2 nam và ít nhất 1 nữ?
A.425 B.375 C.350 D.275
Lời giải:
Đáp án : A
+ Trường hợp 1 : Ban quản trị có 2 nam và 3 nữ:
+ Trường hợp 2 : Ban quản trị có 3 nam và 2 nữ.
+ Trường hợp 3 : Ban quản trị có 4 nam và 1 nữ:
⇒ Số cách lập ra ban quản trị thỏa mãn đầu bài là: 150 + 200 + 75= 425 cách
Câu 9: Có 8 nhà khoa học Toán gồm 6 nam, 2 nữ và 5 nhà khoa học Vật Lí -toàn nam. Hỏi có bao nhiêu cách lập một đội gồm 4 nhà khoa học trong đó có cả nam, nữ, cả Toán, Vật Lí?
A.270 B.185 C.375 D.330
Lời giải:
Đáp án : D
Nếu đã có nữ thì rõ ràng có nhà khoa học Toán, nếu đã có nhà khoa học Vật Lí thì chắc chắn có nam. Do đó ta chỉ cần xét các trường hợp sau:
- Có đúng 1 nữ nhà khoa học Toán, có 2 cách chọn. Lúc này chỉ cần có nhà khoa học Vật Lí là thỏa mãn đề bài, có thể có hoặc không nhà khoa học Toán nam nào khác, số cách chọn 3 nhà khoa học còn lại là
Vậy số cách lập nhóm trong trường hợp này là:
- Có đúng 2 nữ nhà khoa học Toán, có 1 cách chọn. Cũng với ý tưởng như trên, chỉ cần có nhà khoa học Vật Lí là thỏa mãn, số cách chọn 2 nhà khoa học còn lại là
Vậy số cách lập nhóm trong trường hợp này là: 40
⇒ Vậy số cách lập cần tìm là: 290+ 40= 330 cách
Câu 10: Trong một túi đựng 10 viên bi đỏ, 20 viên bi xanh,15 viên bi vàng. Các viên bi có cùng kích cỡ. Số cách lấy ra 5 viên bi và sắp xếp chúng vào 5 ô sao cho 5 ô bi đó có ít nhất một viên bi đỏ.
A.102986240 B.104780240 C.107655240 D.107565240
Lời giải:
Đáp án : C
Bước 1:Chọn ra 5 bi trong đó có ít nhất một viên bi đỏ:
+ Số cách chọn ra 5 viên bi bất kì là
+ Số cách chọn ra 5 viên bi trong đó không có viên bi đỏ nào là
+ Số cách chọn ra 5 viên bi trong đó có ít nhất một viên bi màu đỏ là
Bước 2: Sắp xếp 5 viên bi vừa chọn vào 5 ô:
+ Số cách xếp 5 viên bi vào 5 ô là 5!
+ Theo quy tắc nhân thì có
Câu 11: Trong một tổ học sinh có 5 em gái và 10 em trai. Thùy là một trong 5 em gái và Thiện là một trong 10 em trai đó. Thầy chủ nhiệm chọn một nhóm 5 bạn tham gia buổi văn nghệ sắp tới. Hỏi thầy chủ nhiệm có bao nhiêu cách chọn mà trong đó có ít nhất một trong hai em Thùy hoặc Thiện không được chọn?
A. 2876 B. 2717 C. 3003 D. 1296
Lời giải:
Đáp án : B
Do ở đây việc tìm trực tiếp sẽ có nhiều trường hợp nên ta sẽ giải bài toán bằng cách gián tiếp. Ta sẽ đi tìm bài toán đối.
* Ta đi tìm số cách chọn ra 5 bạn mà trong đó có cả hai bạn Thùy và Thiện.
Chọn nhóm 3 em trong 13 em, trừ Thùy và Thiện thì có
⇒ có 286 cách chọn 5 em trong đó có cả Thùy và Thiện.
*Chọn 5 em bất kì trong số 15 em có
Vậy theo yêu cầu đề bài thì có tất cả: 3003- 286= 2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
Câu 12: Một thầy giáo có 10 cuốn sách khác nhau trong đó có 4 cuốn sách Toán, 3 cuốn sách Lí, 3 cuốn sách Hóa. Thầy muốn lấy ra 5 cuốn và tặng cho 5 em học sinh, mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng cho các em học sinh sao cho sau khi tặng xong, mỗi một trong ba loại sách trên đều còn ít nhất một cuốn.
A.20400 B.24480 C.7200 D.12200
Lời giải:
Đáp án : B
Ta tìm số cách sao cho sau khi tặng sách xong có môn hết sách.
Trường hợp 1 :
Môn Toán hết sách:
Số cách chọn 4 cuốn sách Toán là 1 cách.
Số cách chọn 1 cuốn trong 6 cuốn còn lại là 6 cách.
Vậy có 6 cách chọn sách.
Số cách tặng 5 cuốn sách đó cho 5 em học sinh là 5!= 120 cách.
Vậy có 6.120 = 720 cách.
Trường hợp 2 :
Môn Lí hết sách:
Số cách chọn 3 cuốn sách Lí là 1 cách.
Số cách chọn 2 cuốn trong 7 cuốn còn lại là
Vậy có 21 cách chọn sách.
Số cách tặng 5 cuốn sách đó cho 5 em học sinh là 5!= 120 cách.
Vậy có 21. 120 = 2520 cách.
Trường hợp 3 :
Môn Hóa hết sách: Tương tự trường hợp 2 thì có 2520 cách.
Số cách chọn 5 cuốn bất kì trong 10 cuốn và tặng cho 5 em là
Vậy số cách chọn sao cho sau khi tặng xong, mỗi loại sách trên đều còn lại ít nhất một cuốn là 30240 – 720 – 2520 – 2520 = 24480 cách.
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
- Cách giải bài toán đếm số sử dụng Hoán vị (cực hay có lời giải)
- Phương pháp giải bài toán Hoán vị vòng quanh (cực hay có lời giải)
- Phương pháp giải bài toán Hoán vị lặp (cực hay có lời giải)
- Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)
- Cách giải bài toán đếm số sử dụng Chỉnh hợp (cực hay có lời giải)
- Cách giải bài toán đếm số sử dụng Tổ hợp (cực hay có lời giải)
- Cách giải bài toán đếm hình sử dụng Tổ hợp (cực hay có lời giải)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều

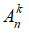
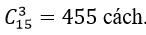
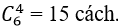
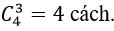
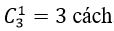
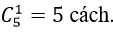
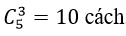
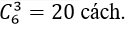
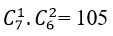
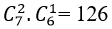
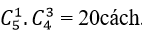
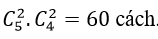
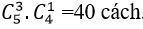
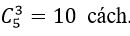
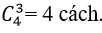
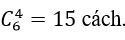
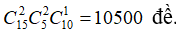
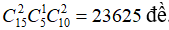
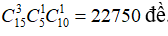
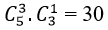
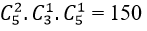
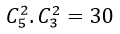
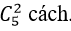
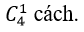
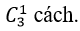
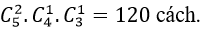
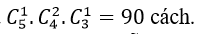
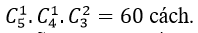
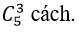
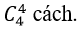
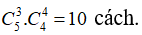
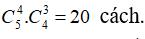
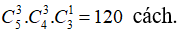
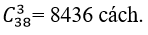
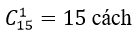
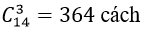
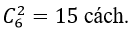
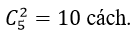
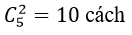
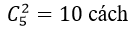
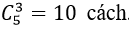
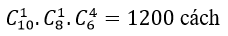
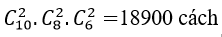
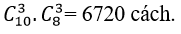
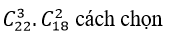
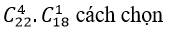
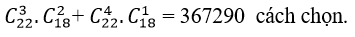
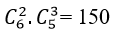
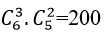
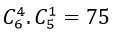
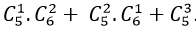
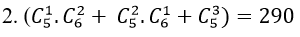
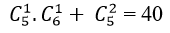
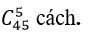
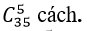
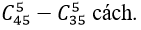
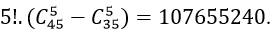
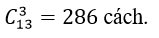
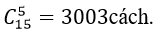
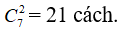
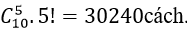



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

