Phương pháp giải bài toán Hoán vị vòng quanh (cực hay có lời giải)
Bài viết Phương pháp giải bài toán Hoán vị vòng quanh với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Phương pháp giải bài toán Hoán vị vòng quanh.
Phương pháp giải bài toán Hoán vị vòng quanh (cực hay có lời giải)
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
A. Phương pháp giải
Định nghĩa: Cho tập hợp X gồm n phần tử. Mỗi cách sắp xếp n phần của X trên một đường tròn gọi là một hoán vị vòng quanh của n phần tử của tập X.
Các cách sắp xếp các phần tử của X trên một đường tròn mà sai khác nhau một phép quay được coi là cùng một hoán vị vòng quanh.
Số các hoán vị vòng quanh của n phần tử khác nhau được tính bởi công thức: Qn=(n-1)!
B. Ví dụ minh họa
Ví dụ 1 : Tổ 1 của lớp 10A1 có 4 học sinh nữ và 6 học sinh nam .Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn.
A.362880 B.128800 C.246800 D.328600
Hướng dẫn giải :
Đáp án : A
Tổ 1 có tất cả 10 học sinh.Mỗi cách xếp 10 học sinh này vào một bàn tròn là một hoán vị vòng quanh của 10 phần tử nên số cách xếp thỏa mãn đề bài là:
9!= 362880 cách xếp.
Ví dụ 2 : Cuối năm học, các học sinh giỏi lớp 11A2 có tổ chức ăn liên hoan. Tổ 1 có 3 học sinh giỏi; tổ 2 có 4 học sinh giỏi; tổ 3 có 2 học sinh giỏi và tổ 4 có 3 học sinh giỏi. Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn?
A.10! B.11! C.12! D.13!
Hướng dẫn giải :
Đáp án : B
Lớp 11A2 có tất cả số học sinh giỏi là: 3+ 4+ 2+ 3= 12 học sinh giỏi
Việc xếp 12 học sinh giỏi này vào một bàn tròn là một hoán vị vòng quanh của 12 phần tử nên số cách xếp thỏa mãn là: 11! cách xếp.
Ví dụ 3 : Tổ 4 của lớp 12A3 có 4 học sinh nữ và 5 học sinh nam . Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn sao cho nhóm học sinh nữ ngồi với nhau; nhóm học sinh nam ngồi với nhau.
A.1280 B.1660 C.2880 D.1860
Hướng dẫn giải :
Đáp án : C
+ Ta coi 4 học sinh nữ là một nhóm X và 5 học sinh nam là nhóm Y.
+ Số cách xếp hai nhóm X và Y vào bàn tròn là (2-1)!= 1 cách .
+ Số cách xếp 4 học sinh nữ trong nhóm X là 4!.
+ Số cách xếp 5 học sinh nam trong nhóm Y là 5!.
⇒ Có: 1. 4!. 5!= 2880 cách xếp thỏa mãn đầu bài.
Ví dụ 4 : Một hội nghị bàn tròn có ba phái đoàn: 4 người miền bắc, 3 người miền trung và 4 người miền nam. Hỏi có bao nhiêu cách xếp chỗ ngồi cho các thành viên sao cho những người có cùng miền thì ngồi gần nhau.
A.7268 B.6912 C.3286 D.4896
Hướng dẫn giải :
Đáp án : B
+ Ta coi: 4 người miền bắc là một nhóm X; 3 người miền trung là một nhóm Y và 4 người miền nam là một nhóm Z .
+ Số cách xếp ba nhóm X; Y; Z vào bàn tròn là: 2!= 2 cách.
+ Số cách xếp 4 người trong nhóm X là : 4!= 24 cách.
+ Số cách xếp 3 người trong nhóm Y là: 3!= 6 cách.
+ Số cách xếp 4 người trong nhóm Z là: 4! = 24 cách.
⇒ Số cách xếp thỏa mãn đầu bài là : 2. 24.6.24= 6912 cách.
Ví dụ 5 : Một nhóm học sinh có 6 nam và 6 nữ. Hỏi có bao nhiêu cách xếp 12 người này vào bàn tròn sao cho hai bạn cùng giới không ngồi cạnh nhau.
A.86400 B.172800 C.43200 D.Đáp án khác
Hướng dẫn giải :
Đáp án : A
+ Xếp 6 bạn nam vào 1 bàn tròn có : 5! Cách.
+ Khi đó giữa hai bạn nam có 1 vách ngăn. Có 6 vách ngăn. Xếp 6 bạn nữ vào 6 vách ngăn đó có 6! Cách.
Theo quy tắc nhân; số cách xếp thỏa mãn đầu bài là: 5!. 6!= 86400
Ví dụ 6 : Trong một buổi dự tiệc có 5 cặp vợ chồng tham gia. Hỏi có bao nhiêu cách xếp 5 cặp này vào một bàn tròn sao cho hai vợ chồng ngồi cạnh nhau.
A.96 B.192 C.768 D.384
Hướng dẫn giải :
Đáp án : C
+ Coi vợ chồng là 1 bó. Xếp 5 bó vào cái bàn tròn có 4! Cách xếp.
+ Với mỗi bó ta có thể đổi chỗ vị trí vợ; chồng cho nhau.
⇒ Với mỗi cặp vợ chồng có 2!= 2 cách xếp
Theo quy tắc nhân; số cách xếp thỏa mãn là: 4!.2.2.2.2.2= 768 cách.
Ví dụ 7 : Một nhóm văn nghệ gồm 4 bạn nữ và x bạn nam ngồi vào một bàn tròn. Biết rằng có 362880 cách xếp các bạn này vào bàn tròn. Hỏi nhóm văn nghệ này có tất cả bao nhiêu người.
A.6 B.5 C.9 D.10
Hướng dẫn giải :
Đáp án : C
+ Nhóm văn nghệ này có tất cả (4+x) bạn.
+ Số cách xếp (4 + x) bạn này vào bàn tròn là: (4+x)!
Theo đầu bài ta có: (4+x)! = 362880= 9!
⇔ 4 + x= 9 ⇔ x= 5
⇒ Nhóm văn nghệ có 5 bạn nam nên cả nhóm này có 4 + 5= 9 bạn
Ví dụ 8 : Lớp 10A1 tổ chức một buổi khen thưởng. Biết tổ 1 có 3 người được khen thưởng; tổ 2 có 2 người; tổ 3 có 4 người và tổ 4 có x người.Xếp những người này vào một bàn tròn và các bạn cùng tổ ngồi liền kề với nhau. Biết có 10368 cách xếp thỏa mãn. Tìm x ( biết x>0)?
A.1 B.2 C.3 D.4
Hướng dẫn giải :
Đáp án : B
+ Số cách xếp 4 tổ vào 1 bàn tròn là 3!.
+ Tổ 1 có 3 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 3 bạn này có 3! Cách.
+ tổ 2 có 2 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 2 bạn này có 2! Cách.
+ Tổ 3 có 4 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 4 người này có 4! Cách.
+ Tổ 4 có x bạn ngồi liền kề với nhau. Hoán đổi vị trí của x người này có x! cách.
Theo quy tắc nhân; số cách xếp thỏa mãn là:
3!. 3!.2!. 4!.x!= 10368
⇔ x!= 6 ⇔ x= 2
C. Bài tập trắc nghiệm
Câu 1 : Trong một buổi dự tiệc; có 3 người phụ nữ và 4 người đàn ông cùng ngồi vào một bàn tròn. Hỏi có bao nhiêu cách xếp chỗ ngồi cho những người này?
A.720 B.120 C.5040 D.2080
Lời giải:
Đáp án : A
Việc xếp 3+ 4= 7 người này vào một bàn tròn là một hoán vị vòng quanh của 7 phần tử nên có: 6!= 720 cách xếp thỏa mãn.
Câu 2 : Trong một buổi dạ hội; có 4 người đàn ông và 4 phụ nữ cùng ngồi vào một bàn tròn. Hỏi có bao nhiêu cách xếp sao cho nam; nữ ngồi xen kẽ nhau.
A.36 B.144 C.576 D.128
Lời giải:
Đáp án : B
+ Xếp 4 bạn nam vào 4 ghế cách đều nhau có 3!= 6 cách.
( khi xếp vào bàn tròn thì vị trí người đầu tiên không quan trọng ) .
+ Xếp 4 bạn nữ vào 4 vị trí còn lại có 4!= 24 cách.
+ Theo quy tắc nhân có: 6.24= 144 cách thỏa mãn.
Câu 3 : Có 5 học sinh nam trong đó có bạn Hải và 3 học sinh nữ trong đó có bạn Liên. Hỏi có bao nhiêu cách xếp tám học sinh nói trên ngồi vào một bàn tròn sao cho hai bạn Hải và Liên không ngồi cạnh nhau ? (Hai cách xếp chỉ khác nhau một phép quay được coi là như nhau).
A.1440 B.5040 C.2880 D.3600
Lời giải:
Đáp án : D
- Số cách xếp 8 học sinh vào bàn tròn là hoán vị vòng quanh của tập 8 phần tử nên có :
7 != 5040 cách xếp.
- Ta tính số cách xếp 8 học sinh vào bàn tròn sao cho hai bạn Hải, Liên ngồi cạnh nhau :
+ Ta coi hai bạn Hải ; Liên là một phần tử X
+ Số cách xếp X và 6 học sinh khác vào bàn tròn là hoán vị vòng quanh của tập có 7 phần tử nên có : 6 != 720 cách xếp.
+ Khi đổi chỗ hai bạn Hải ; Liên ta có thêm một cách xếp.
⇒ Số cách xếp thỏa mãn là : 720. 2= 1440 cách.
Suy ra : số cách xếp 8 học sinh vào bàn tròn sao cho hai bạn Hải và Liên không ngồi cạnh nhau là : 5040 – 1440= 3600 cách
Câu 4 : Có 4 nhóm đại sứ quán nước ngoài gồm: 3 người nước Anh; 4 người nước Pháp ; 4người nước Mỹ và 2 người nước Lào. Hỏi có bao nhiêu cách xếp họ vào một bàn tròn sao cho các đại sứ quán của cùng 1 nước ngồi cạnh nhau?
A.41472 B.20736 C.6912 D.Đáp án khác
Lời giải:
Đáp án : A
+ Ta coi; 3 người nước Anh là nhóm X; 4 người nước Pháp là nhóm Y; 4 người nước Mỹ là nhóm Z và 2 người nước Lào là nhóm T.
+ Số cách xếp 4 nhóm X; Y; Z; T vào bàn tròn là: 3! = 6 cách.
+ Số cách xếp 3 người nhóm X là một hoán vị của tập có 3 phần tử có: 3!= 6 cách.
+ Số cách xếp 4 người nhóm Y là 4!= 24 cách.
+ Số cách xếp 4 người nhóm Z là 4!= 24 cách.
+ Số cách xếp 2 người nhóm T là 2!= 2 cách.
⇒ Số cách xếp thỏa mãn đầu bài là:
6.6.24.24.2= 41472 cách.
Câu 5 : Có bao nhiêu cách sắp xếp 6 người (trong đó có một cặp vợ chồng) vào một bàn tròn, sao cho vợ chồng ngồi cạnh nhau?
A.120 B.720 C.48 D.24
Lời giải:
Đáp án : C
+ Coi cặp vợ chồng đó là phần tử X.
+ Số cách xếp phần tử X và 4 người còn lại vào bàn tròn là hoán vị vòng quanh của 5 phần tử nên có: 4!= 24 cách xếp.
+ Ta có 2!= 2 cách xếp vợ chồng đó.
⇒ Số cách xếp thỏa mãn đầu bài là: 24. 2= 48 cách .
Câu 6 : Trong buổi dự tiệc có 10 người trong đó có 1 cặp vợ chồng. Hỏi có bao nhiêu cách xếp 10 người này vào bàn tròn sao cho hai vợ chồng đó không ngồi cạnh nhau.
A.282240 B.146800 C.245200 D.186400
Lời giải:
Đáp án : A
+ Xếp người chồng trước: 1 cách.
+ Vì vợ chồng không được ngồi cạnh nhau nên có 7 cách xếp vị trí người vợ( trừ hai ghế sát chồng).
+ Xếp 8 người khác vào 8 vị trí còn lại: có 8! Cách xếp.
Theo quy tắc nhân có: 1. 7. 8!= 282240 cách.
Câu 7 : Một nhóm học sinh có 8 người trong đó có lớp trưởng; bí thư và lớp phó. Hỏi có bao nhiêu cách xếp 8 bạn này vào bàn tròn sao cho 3 bạn cán bộ lớp không ngồi cạnh nhau.
A.6420 B.2860 C.4320 D.5420
Lời giải:
Đáp án : C
- Số cách xếp 8 người này vào bàn tròn là : 7! (1)
- Ta tính só cách xếp 8 bạn này vào bàn tròn sao cho ba bạn cán bộ lớp ngồi cạnh nhau. Coi ba bạn cán bộ lớp là phần tử X.
+ Có 5! Cách xếp 5 bạn còn lại và X vào bàn tròn.
+ Hoán đổi vị trí 3 bạn trong X có 3! Cách.
=> có 5!.3! cách xếp sao cho ba bạn cán bộ lớp ngồi cạnh nhau.(2)
Từ (1) và (2) suy ra số cách xếp thỏa mãn đầu bài là: 7!- 5!. 3!= 4320 cách.
Câu 8 : Có bao nhiêu cách xếp 8 bạn nữ và 6 bạn nam vào bàn tròn sao cho các bạn nam không ngồi cạnh nhau .

Lời giải:
Đáp án : B
+ Xếp 8 bạn nữ vào 8 ghế bàn tròn có 7! Cách.
+ Khi đó giữa 8 bạn nữ tạo ra 8 vách ngăn. Ta xếp 6 bạn nam vào 8 vách ngăn : có 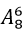
Theo quy tắc nhân có: 7!. 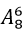
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
- Cách giải bài toán đếm số sử dụng Hoán vị (cực hay có lời giải)
- Phương pháp giải bài toán Hoán vị lặp (cực hay có lời giải)
- Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)
- Cách giải bài toán đếm số sử dụng Chỉnh hợp (cực hay có lời giải)
- Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)
- Cách giải bài toán đếm số sử dụng Tổ hợp (cực hay có lời giải)
- Cách giải bài toán đếm hình sử dụng Tổ hợp (cực hay có lời giải)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

