Tứ phân vị của mẫu số liệu ghép nhóm là gì lớp 11 (chi tiết nhất)

Bài viết Tứ phân vị của mẫu số liệu ghép nhóm là gì lớp 11 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Tứ phân vị của mẫu số liệu ghép nhóm.

Tứ phân vị của mẫu số liệu ghép nhóm là gì lớp 11 (chi tiết nhất)

1. Tứ phân vị của mẫu số liệu ghép nhóm

Cho mẫu số liệu ghép nhóm:

Nhóm	[a1; a2)	…	[ai; ai + 1)	…	[ak; ak + 1)
Tần số	m1	…	mi	…	mk

Để tính tứ phân vị thứ nhất Q₁ của mẫu số liệu ghép nhóm trên, trước hết ta xác định nhóm chứa Q₁, giả sử đó là nhóm thứ p: [a_p; a_{p + 1}). Khi đó,

$Q_1=a_p+\frac{\frac{n}{4}-\left(m_1+\mathrm{...}+m_{p-1}\right)}{m_p}\left(a_{p+1}-a_p\right)$.

Với n là cỡ mẫu, m_p là tần số nhóm p. Với p = 1, ta quy ước m₁ + … + m_{p – 1} = 0.

Để tính tứ phân vị thứ nhất Q₃ của mẫu số liệu ghép nhóm trên, trước hết ta xác định nhóm chứa Q₃, giả sử đó là nhóm thứ p: [a_p; a_{p + 1}). Khi đó,

$Q_3=a_p+\frac{\frac{3n}{4}-\left(m_1+\mathrm{...}+m_{p-1}\right)}{m_p}\left(a_{p+1}-a_p\right)$.

Với n là cỡ mẫu, m_p là tần số nhóm p. Với p = 1, ta quy ước m₁ + … + m_{p – 1} = 0.

Tứ phân vị thứ hai Q₂ chính là trung vị M_e.

Nhận xét: Ta cũng có thể xác định nhóm chứa tứ phân vị thứ r nhờ tính chất: có khoảng $\left(\frac{rn}{4}\right)$ giá trị nhỏ hơn tứ phân vị này.

Ý nghĩa: Các tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ cho các tứ phân vị của mẫu số liệu gốc, chúng chia mẫu số liệu thành 4 phần, mỗi phần chứa 25% giá trị.

Chú ý: Nếu tứ phân vị thứ k là $\frac{1}{2}\left(x_m+x_{m+1}\right)$, trong đó x_m và x_{m + 1} thuộc hai nhóm liên tiếp, ví dụ như x_m ∈ [a_{j – 1}; a_j) và x_{m + 1} ∈ [a_j; a_{j + 1}) thì ta lấy Q_k = a_j.

2. Ví dụ minh họa về tứ phân vị của mẫu số liệu ghép nhóm

Ví dụ 1. Mức thưởng tết mà các công nhân của một nhà máy nhận được như sau:

Mức thưởng (triệu đồng)	[5; 10)	[10; 15)	[15; 20)	[20; 25)
Số người	8	16	12	5

Tính tứ phân vị thứ nhất (làm tròn kết quả đến hàng phần mười của triệu đồng).

Hướng dẫn giải

Cỡ mẫu là: n = 8 + 16 + 12 + 5 = 41.

Gọi x₁; …; x₄₁ là mức thưởng tết của 41 công nhân và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, tứ phân vị thứ nhất là $\frac{1}{2}\left(x_{10}+x_{11}\right)$. Do x₁₀, x₁₁ thuộc nhóm [10; 15) nên nhóm này chứa Q₁.

Ta có: p = 2, m₂ = 16, a₂ = 10, m₁ = 8, a₃ – a₂ = 5 nên $Q_1=10+\frac{\frac{41}{4}-8}{16}\cdot 5\approx 10,7$.

Vậy tứ phân vị thứ nhất là khoảng 10,7 triệu đồng.

Ví dụ 2. Kết quả khảo sát về chiều cao (cm) của một số học sinh lớp 11 được cho bởi bảng sau:

Chiều cao	[150; 155)	[155; 160)	[160; 165)	[165; 170)	[170; 175)
Số học sinh	6	8	12	10	4

Tìm tứ phân vị thứ ba của mẫu số liệu trên.

Hướng dẫn giải

Cỡ mẫu là: n = 6 + 8 + 12 + 10 + 4 = 40.

Gọi x₁; …; x₄₀ là chiều cao của 40 học sinh lớp 11 và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, tứ phân vị thứ ba là $\frac{x_{30}+x_{31}}{2}$. Do 2 giá trị x₃₀, x₃₁ đều thuộc nhóm [165; 170) nên nhóm này chứa tứ phân vị thứ ba.

Do đó, p = 4, m₄ = 10, a₄ = 165, m₁ + m₂ + m₃ = 26, a₅ – a₄ = 5 và ta có:

$Q_3=165+\frac{\frac{3.40}{4}-26}{10}.5=167$ (cm).

Vậy tứ phân vị thứ ba của mẫu số liệu là 167 cm.

Ví dụ 3. Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho bởi bảng sau:

Tuổi thọ	[2; 2,5)	[2,5; 3)	[3; 3,5)	[3,5; 4)	[4; 4,5)	[4,5; 5)
Tần số	6	8	14	12	7	3

Tìm tứ phân vị của mẫu số liệu trên (làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Gọi x₁; …; x₅₀ là tuổi thọ của 50 bình ắc quy và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.

+ Trung vị là $\frac{x_{25}+x_{26}}{2}$. Do 2 giá trị x₂₅, x₂₆ đều thuộc nhóm [3; 3,5) nên nhóm này chứa trung vị. Do đó, p = 3, m₃ = 14, a₃ = 3, m₁ + m₂ = 14, a₄ – a₃ = 0,5 và:

$M_e=3+\frac{\frac{50}{2}-14}{14}.0,5\approx 3,4$.

+ Tứ phân vị thứ nhất là x₁₃. Do x₁₃ thuộc nhóm [2,5; 3) nên nhóm này chứa Q₁. Ta có: p = 2, m₂ = 8, a₂ = 2,5, m₁ = 6, a₃ – a₂ = 0,5 và $Q_1=2,5+\frac{\frac{50}{4}-6}{8}\cdot 0,5\approx 2,9$

+ Tứ phân vị thứ ba là x₃₈. Do giá trị x₃₈ đều thuộc nhóm [3,5; 4) nên nhóm này chứa Q₃. Do đó, p = 4, m₄ = 12, a₄ = 3,5, m₁ + m₂ + m₃ = 28, a₅ – a₄ = 0,5 và:

$Q_3=3,5+\frac{\frac{3.50}{4}-28}{12}.0,5\approx 3,9$

Vậy $Q_1\approx 2,9;Q_2\approx 3,4;Q_3\approx 3,9$.

3. Bài tập về tứ phân vị của mẫu số liệu ghép nhóm

Bài 1. Cho bảng tần số ghép nhóm sau đây:

Nhóm	Tần số
[2; 6)	10
[6; 10)	19
[10; 14)	16
[14; 18)	10
[18; 22)	6

Tính tứ phân vị thứ nhất của mẫu số liệu.

Bài 2. Bảng tần số ghép nhóm dưới đây thông kê số cân nặng trung bình của học sinh lớp 12K:

Cân nặng	[40; 45)	[45; 50)	[50; 55)	[55; 60)	[60; 65)
Số học sinh	7	10	13	9	5

Tìm tứ phân vị thứ ba của mẫu số liệu trên.

Bài 3. Bảng dưới đây thống kê về số sách cũ mà các bạn học sinh lớp 11I mang đến để tặng cho thư viện trường A:

Số sách	[1; 3]	[4; 6]	[7; 9]	[10; 12]	[13; 15]
Số học sinh	6	12	15	12	8

Hãy tính tứ phân của mẫu số liệu trên.

Bài 4. Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại của một số học sinh khối 11 như sau:

Thời gian	[0; 30)	[30; 60)	[60; 90)	[90; 120)	[120; 150)
Số người	8	12	15	16	6

a) Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Có ý kiến cho rằng có trên 25% người sử dụng điện thoại không ít hơn 90 phút một ngày. Ý kiến trên có đúng không?

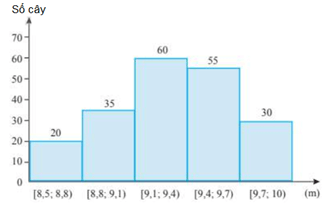
Bài 5. Biểu đồ dưới đây cho biết chiều cao của 200 cây keo trồng được 3 năm ở nông trường A:

Lập bảng tần số ghép nhóm và tính tứ phân vị của mẫu số liệu được biểu diễn ở biểu đồ trên.

Xem thêm các dạng bài tập Toán lớp 11 sách mới hay, chi tiết khác:

• Mốt của mẫu số liệu ghép nhóm là gì

• Điểm thuộc, không thuộc mặt phẳng là gì

• Các tính chất thừa nhận của hình học không gian

• Cách xác định một mặt phẳng

• Hình chóp là gì

---