Lý thuyết Phương trình bậc hai với hệ số thực lớp 12 (hay, chi tiết)
Bài viết Lý thuyết Phương trình bậc hai với hệ số thực lớp 12 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm Lý thuyết Phương trình bậc hai với hệ số thực.
Lý thuyết Phương trình bậc hai với hệ số thực
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Bài giảng: Bài 4 : Phương trình bậc hai với hệ số thực - Thầy Trần Thế Mạnh (Giáo viên VietJack)
A. Tóm tắt lý thuyết
1. Căn bậc hai của số phức: Cho số phức w. Mỗi số phức z thỏa mãn z2 = w được gọi là một căn bậc hai của w .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai ax2 + bx + c = 0 (a, b, c ∈ R; a ≠ 0). Xét Δ = b2 - 4ac, ta có
• Δ = 0: phương trình có nghiệm thực x = -b/2a .
• Δ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức: 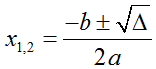
• Δ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức: 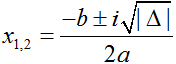
** Chú ý.
- Mọi phương trình bậc n: A0zn + A1zn-1 + ... + An-1z + An = 0 luôn có n nghiệm phức (không nhất thiết phân biệt).
- Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x1, x2 (thực hoặc phức). Ta có hệ thức Vi–ét
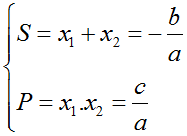
B. Kĩ năng giải bài tập
1. Dạng 1: Tìm căn bậc hai của một số phức
• Trường hợp w là số thực: Nếu a là một số thực
+ a < 0, a có các căn bậc hai là ±i√|a| .
+ a = 0, a có đúng một căn bậc hai là 0.
+ a > 0 , a có hai căn bậc hai là ±√a.
Ví dụ 1: Ta có hai căn bậc hai của – 1 là i và -i. Hai căn bậc hai của -a2 (a là số thực khác 0) là ai và -ai.
• Trường hợp w = a + bi (a,b ∈ R, b ≠ 0)
Gọi z = x + yi (x, y ∈ R) là một căn bậc hai của w khi và chỉ khi z2 = w, tức là
(x + yi)2 = a + bi ⇔ x2 - y2 + 2xyi = a +bi ⇔
Mỗi cặp số thực (x; y) nghiệm đúng hệ phương trình trên cho ta một căn bậc hai x + yi của số phức w = a + bi.
Ví dụ 2: Tìm các căn bậc hai của w = -5 + 12i.
Lời giải:
Gọi z = x + yi (x, y ∈ R) là một căn bậc hai của số phức w = -5 _ 12i.
Ta có z2 = w ⇔ (x + yi)2 = -5 + 12i ⇔
Vậy w = -5 + 12i có hai căn bậc hai là 2 + 3i và -2 - 3i.
2. Dạng 2: Giải phương trình bậc hai với hệ số thực và các dạng toán liên quan
• Giải các phương trình bậc hai với hệ số thực
Ví dụ 3: Giải phương trình bậc hai sau: z2 - z + 1 = 0
Lời giải:
Ta có ± = b2 -4ac = -3 < 0
Phương trình có hai nghiệm phức phân biệt là 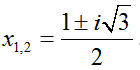
• Giải phương trình quy về phương trình bậc hai với hệ số thực
Phương pháp 1: Phân tích đa thức thành nhân tử:
– Bước 1: Nhẩm 1 nghiệm đặc biệt của phương trình.
+ Tổng các hệ số trong phương trình là 0 thì phương trình có một nghiệm x = 1.
+ Tổng các hệ số biến bậc chẵn bằng tổng các hệ số biến bậc lẻ thì phương trình có một nghiệm x = -1.
Định lý Bơdu:
Phần dư trong phép chia đa thức f(x) cho x - a bằng giá trị của đa thức f(x) tại x = a
Tức là f(x) = (x - a)g(x) - f(a)
Hệ quả: Nếu f(a) = 0 thì f(x)⋮ (x - a)
Nếu f(x)⋮(x - a) thì f(a) = 0 hay f(x) = 0 có một nghiệm x = a
– Bước 2: Đưa phương trình về phương trình bậc nhất hoặc bậc hai bằng cách hân tích đa thức ở vế trái của phương trình thành nhân tử (dùng hẳng đảng thức, chia đa thức hoặc sử dụng lược đồ Hoocne) như sau:
Với đa thức f(x) = anxn + an-1xn-1 + ... + a1x + a0 chia cho x - a có thương là g(x) = bn-1xn-1 + bn-2xn-2 + ... + b1x + b0 dư r
| an | an-1 | an-2 | a2 | a1 | a0 | |
| a | bn-1 = an | bn-2 = abn-1 | bn-3 = abn-2 | b1 = ab2 | b0 = ab1 + a1 | r = ab0 + b0 |
– Bước 3: Giải phương trình bậc nhất hoặc bậc hai, kết luận nghiệm
Phương pháp 2: Đặt ẩn phụ:
– Bước 1: Phân tích phương trình thành các đại lượng có dạng giống nhau.
– Bước 2: Đặt ẩn phụ, nêu điều kiện của ẩn phụ (nếu có).
– Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất, bậc hai với ẩn mới.
– Bước 4: Giải phương trình, kết luận nghiệm.
B. Kĩ năng sử dụng máy tính bỏ túi
1. Chọn chế độ tính toán với số phức: MODE 2 màn hình hiện CMPLX.
Nhập số thuần ảo i: Phím ENG
2. Tìm các căn bậc hai của một số phức
Ví dụ 5: Khai căn bậc hai số phức z = -3-4i có kết quả:
Lời giải:
Cách 1:
– Mode 2 (CMPLX)
– Nhập hàm X2
– Sử dụng phím CALC, nhập từng giá trị vào, giá trị nào ra kết quả bằng z thì ta nhận.
Cách 2:
– Mode 1 (COMP)
– Nhấn Shift + (Pol), ta nhập Pol(-3;4)
– Nhấn Shift – (Rec), ta nhập Rec(√X,Y:2), ta thu được kết quả X = 1; Y = 2.
– Vậy 2 số phức cần tìm là 1 + 2i và -1 - 2i.
Lý thuyết và bài tập trắc nghiệm có đáp án và lời giải chi tiết Toán lớp 12 khác:
- Lý thuyết Số phức
- Lý thuyết Cộng, trừ và nhân số phức
- Lý thuyết Phép chia số phức
- Lý thuyết Phương trình bậc hai với hệ số thực
- Lý thuyết tổng hợp chương Số phức
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

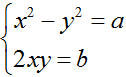
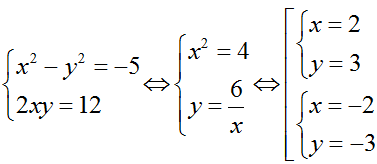



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

