Lý thuyết Phương trình mặt phẳng lớp 12 (hay, chi tiết)

---

---

Bài viết Lý thuyết Phương trình mặt phẳng lớp 12 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm Lý thuyết Phương trình mặt phẳng.

Lý thuyết Phương trình mặt phẳng

Bài giảng: Bài 2: Phương trình mặt phẳng - Thầy Trần Thế Mạnh (Giáo viên VietJack)

A. Tóm tắt lý thuyết

I. Vectơ pháp tuyến của mặt phẳng

    • Vectơ n→ ≠ 0→ là vectơ pháp tuyến (VTPT) nếu giá của n→ vuông góc với mặt phẳng (α)

    • Chú ý:

    - Nếu n→ là một VTPT của mặt phẳng (α) thì kn→ cũng là một VTPT của mặt phẳng (α).

    - Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.

    - Nếu u→, v→ có giá song song hoặc nằm trên mặt phẳng (α) thì n→ = [u→, v→] là một VTPT của (α)

II. Phương trình tổng quát của mặt phẳng

    - Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:

    Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0

    - Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).

    - Phương trình mặt phẳng đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - x_o) + B(y - y_o) + C(z - z_o) = 0 .

    • Các trường hợp riêng

    Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0

    - Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.

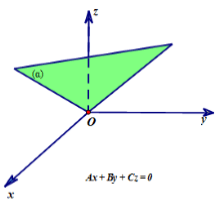
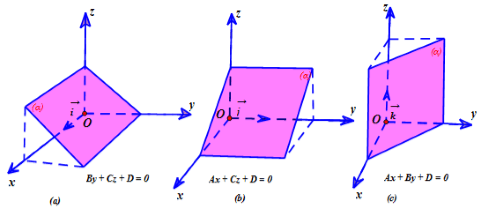
    - Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.

    - Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.

    - Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.

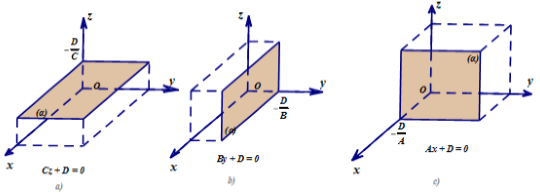
    - Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).

    - Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).

    - Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).

    Chú ý:

    - Nếu trong phương trình (α) không chứa ẩn nào thì (α) song song hoặc chứa trục tương ứng.

    - Phương trình mặt phẳng theo đoạn chắn (α): 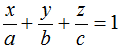. Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0), (0; b; 0), (0; 0; c) với abc ≠ 0.

III. Khoảng cách từ một điểm đến một mặt phẳng.

    • Trong không gian Oxyz, cho điểm M_o(x_o; y_o; z_o) và mặt phẳng (α): Ax + By + Cz + D = 0

    Khi đó khoảng cách từ điểm M_o đến mặt phẳng (α) được tính:

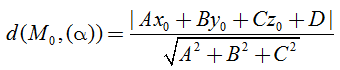
IV. Góc giữa hai mặt phẳng

    Trong không gian Oxyz, cho hai mặt phẳng (α): A₁x + B₁y + C₁z + D₁ = 0 và (β): A₂x + B₂y + C₂z + D₂ = 0

    Góc giữa (α) và (β) bằng hoặc bù với góc giữa hai VTPT n_α→, n_β→. Tức là:

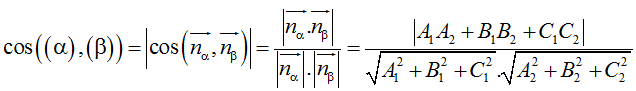
B. Kĩ năng giải bài tập

    Một số dạng bài tập về viết phương trình mặt phẳng

    Dạng 1: Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến của nó.

    Phương pháp giải

    Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 2: Viết phương trình mặt phẳng (α) đi qua 1 điểm M_o(x_o; y_o; z_o) và song song với 1 mặt phẳng (β): Ax + By + Cz + D = 0 cho trước.

    Phương pháp giải

    Cách 1: Thực hiện theo các bước sau:

    1. VTPT của (β) là n_β→ = (A; B; C)

    2. (α) // (β) nên VTPT của mặt phẳng (α) là n_α→ = n_β→ = (A; B; C)

    3. Phương trình mặt phẳng (α): A(x - x₀) + B(y - y₀) + C(z - z₀) = 0

    Cách 2:

    1. Mặt phẳng (α) // (β) nên phương trình (P) có dạng: Ax + By + Cz + D' = 0 (*), với D' ≠ D.

    2. Vì (P) qua 1 điểm M_o(x_o; y_o; z_o) nên thay tọa độ M_o(x_o; y_o; z_o) vào (*) tìm được D'.

    Dạng 3: Viết phương trình mặt phẳng (α) đi qua 3 điểm A, B, C không thẳng hàng.

    Phương pháp giải

    1. Tìm tọa độ các vectơ: AB→, AC→

    2. Vectơ pháp tuyến của (α) là: n_α→ = [AB→, AC→]

    3. Điểm thuộc mặt phẳng: A (hoặc B hoặc C).

    4. Viết phương trình mặt phẳng qua 1 điểm và có VTPT n_α→

    Dạng 4: Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng Δ

    Phương pháp giải

    1. Tìm VTCP của Δ là u_Δ→

    2. Vì (α) ⊥ Δ nên (α) có VTPT n_α→ = u_Δ→

    3. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT n_α→

    Dạng 5: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ, vuông góc với mặt phẳng (β)

    Phương pháp giải

    1. Tìm VTPT của (β) là n_β→

    2. Tìm VTCP của Δ là u_Δ→

    3. VTPT của mặt phẳng (α) là: n_α→ = [n_β→; u_Δ→]

    4. Lấy một điểm M trên Δ

    5. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 6: Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (β)

    Phương pháp giải

    1. Tìm VTPT của (β) là n_β→

    2. Tìm tọa độ vectơ AB→

    3. VTPT của mặt phẳng (α) là: n_α→ = [n_β→, AB→]

    4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 7: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ và song song với Δ' (Δ, Δ' chéo nhau).

    Phương pháp giải

    1. Tìm VTCP của Δ và Δ' là u_Δ→ và u_Δ'→

    2. VTPT của mặt phẳng (α) là: n_α→ = [u_Δ→, u_Δ'→]

    3. Lấy một điểm M trên Δ

    4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 8: Viết phương trình mặt phẳng (α)hứa đường thẳng Δ và 1 điểm M

    Phương pháp giải

    1. Tìm VTCP của Δ là u_Δ→, lấy 1 điểm N trên Δ. Tính tọa độ MN→

    2. VTPT của mặt phẳng (α) là: n_α→ = [u_α→; MN→]

    3. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 9: Viết phương trình mặt phẳng (α) chứa 2 đường thẳng cắt nhau Δ và Δ'

    Phương pháp giải

    1. Tìm VTCP của Δ và Δ' là u_Δ→ và u_Δ'→

    2. VTPT của mặt phẳng (α) là: n_α→ = [u→_Δ; u_Δ'→]

    3. Lấy một điểm M trên Δ

    4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 10: Viết phương trình mặt phẳng (α) chứa 2 song song Δ và Δ'

    Phương pháp giải

    1. Tìm VTCP của Δ và Δ' là u_Δ→ và u_Δ'→, lấy M ∈ Δ, N ∈ Δ'

    2. VTPT của mặt phẳng (α) là: n_α→ = [u_Δ→; MN→]

    3.Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 11: Viết phương trình mặt phẳng (α) đi qua một điểm M và song song với hai đường thẳng Δ và Δ' chéo nhau cho trước.

    Phương pháp giải

    1. Tìm VTCP của Δ và Δ’ là u_Δ→ và u_Δ'→

    2. VTPT của mặt phẳng (α) là: n_α→ = [u_Δ→; u_Δ'→]

    3.Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 12: Viết phương trình mặt phẳng (α) đi qua một điểm M và vuông góc với hai mặt phẳng (P), (Q) cho trước.

    Phương pháp giải

    1. Tìm VTPT của (P) và (Q) là n_P→ và n_Q→

    2. VTPT của mặt phẳng (α) là: n_α→ = [n_P→; n_Q→]

    3.Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

    Dạng 13: Viết phương trình mặt phẳng (α) song song với mặt phẳng (β) và cách (β): Ax + By + Cz + D = 0 một khoảng k cho trước.

    Phương pháp giải

    1. Trên mặt phẳng (β) chọn 1 điểm M.

    2. Do (α) // (β) nên (α) có phương trình Ax + By + Cz + D' = 0 (D' ≠ D).

    3. Sử dụng công thức khoảng cách d((α), (β)) = d(M, (β)) = k để tìm D'.

    Dạng 14: Viết phương trình mặt phẳng (α) song song với mặt phẳng (β): Ax + By + Cz + D = 0 cho trước và cách điểm M một khoảng k cho trước.

    Phương pháp giải

    1. Do (α) // (β) nên (α) có phương trình Ax + By + Cz + D' = 0 (D' ≠ D).

    2. Sử dụng công thức khoảng cách d(M, (α)) = k để tìm D'.

    Dạng 15: Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S).

    Phương pháp giải

    1. Tìm tọa độ tâm I và tính bán kính của mặt cầu (S)

    2. Nếu mặt phẳng (α) tiếp xúc với mặt cầu (S) tại M ∈ (S) thì mặt phẳng (α) đi qua điểm M và có VTPT là MI→

    3. Khi bài toán không cho tiếp điểm thì ta phải sử dụng các dữ kiện của bài toán tìm được VTPT của mặt phẳng và viết phương trình mặt phẳng có dạng: Ax + By + Cz + D = 0 (D chưa biết).

    Sử dụng điều kiện tiếp xúc: d(I,(α)) = R để tìm D.

    Dạng 16: Viết phương trình mặt phẳng (α) chứa một đường thẳng Δ và tạo với một mặt phẳng (β): Ax + By + Cz + D = 0 cho trước một góc φ cho trước.

    Phương pháp giải

    1. Tìm VTPT của (β) là n_β→

    2. Gọi n_α→(A'; B'; C')

    3. Dùng phương pháp vô định giải hệ:

    4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

Lý thuyết và bài tập trắc nghiệm có đáp án và lời giải chi tiết Toán lớp 12 khác:

• Lý thuyết Hệ tọa độ trong không gian
• Lý thuyết Phương trình mặt phẳng
• Lý thuyết Phương trình đường thẳng trong không gian
• Lý thuyết tổng hợp chương Phương pháp tọa độ trong không gian

---

---

---