Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và vận dụng đo mức độ rủi ro lớp 12 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và vận dụng đo mức độ rủi ro lớp 12 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và vận dụng đo mức độ rủi ro.

Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và vận dụng đo mức độ rủi ro lớp 12 (cách giải + bài tập)

1. Phương pháp giải

Xét mẫu số liệu ghép nhóm cho bởi công thức sau:

Số trung bình cộng của mẫu số liệu ghép nhóm trên được tính bằng công thức

$\overline{x}=\frac{1}{n}\left(n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k\right)$.

Phương sai: Phương sai của mẫu số liệu ghép nhóm, kí hiệu S², được tính bởi công thức $S^2=\frac{1}{n}\left[n_1{\left(c_1-\overline{x}\right)}^2+n_2{\left(c_2-\overline{x}\right)}^2+\mathrm{...}+n_k{\left(c_k-\overline{x}\right)}^2\right]$.

Trong đó n = n₁ + ...+ n_k là cỡ mẫu; $\overline{x}=\frac{1}{n}\left(n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k\right)$.

Hoặc phương sai của mẫu số liệu ghép nhóm có thể được tính theo công thức sau:

$S^2=\frac{1}{n}\left(n_1{c_1}^2+n_2{c_2}^2+\mathrm{...}+n_k{c_k}^2\right)-{\overline{x}}^2$.

Độ lệch chuẩn: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu S là căn bậc hai số học của phương sai, nghĩa là $S=\sqrt{S^2}$.

2. Ví dụ minh họa

Ví dụ 1. Cân nặng của một số quả mít trong một khu vườn được thống kê ở bảng sau:

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả các phép tính làm tròn đến hàng phần trăm).

Hướng dẫn giải:

Ta có bảng thống kê có giá trị đại diện

Cỡ mẫu n = 50.

Số trung bình của mẫu số liệu ghép nhóm là $\overline{x}=\frac{6.5+12.7+19.9+9.11+4.13}{50}=\mathrm{8,72}$.

Phương sai của mẫu số liệu ghép nhóm là:

$S^2=\frac{{6.5}^2+{12.7}^2+{19.9}^2+{9.11}^2+{4.13}^2}{50}-{\mathrm{8,72}}^2\approx \mathrm{4,80}$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S=\sqrt{\mathrm{4,80}}\approx \mathrm{2,19}$.

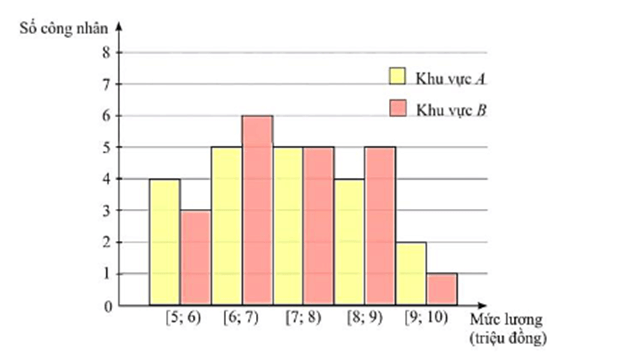
Ví dụ 2. Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực A và B.

a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu đó.

b) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì công nhân ở khu vực nào có mức lương khởi điểm đồng đều hơn?

Hướng dẫn giải:

a) Ta có bảng sau

b) Xét mẫu số liệu khu vực A

Cỡ mẫu n = 20.

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x_A}=\frac{\mathrm{4.5,5}+\mathrm{5.6,5}+\mathrm{5.7,5}+\mathrm{4.8,5}+\mathrm{2.9,5}}{20}=\mathrm{7,25}$.

Phương sai: $S_A^2=\frac{{\mathrm{4.5,5}}^2+{\mathrm{5.6,5}}^2+{\mathrm{5.7,5}}^2+{\mathrm{4.8,5}}^2+{\mathrm{2.9,5}}^2}{20}-{\mathrm{7,25}}^2=\mathrm{1,5875}$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S_A=\sqrt{\mathrm{1,5875}}\approx \mathrm{1,26}$.

Xét mẫu số liệu khu vực B

Cỡ mẫu n = 20.

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x_B}=\frac{\mathrm{3.5,5}+\mathrm{6.6,5}+\mathrm{5.7,5}+\mathrm{5.8,5}+\mathrm{1.9,5}}{20}=\mathrm{7,25}$.

Phương sai: $S_B^2=\frac{{\mathrm{3.5,5}}^2+{\mathrm{6.6,5}}^2+{\mathrm{5.7,5}}^2+{\mathrm{5.8,5}}^2+{\mathrm{1.9,5}}^2}{20}-{\mathrm{7,25}}^2=\mathrm{1,2875}$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là $S_B=\sqrt{\mathrm{1,2875}}\approx \mathrm{1,13}$.

Vì S_A > S_B nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực B đồng đều hơn của công nhân khu vực A.

3. Bài tập tự luyện

Bài 1. Đo chiều cao (tính bằng cm) của 500 học sinh trong một trường THPT ta thu được kết quả như sau:

Độ lệch chuẩn của mẫu số liệu trên là

A. 161,4;

B. 14,48;

C. 8,2;

D. 3,85.

Hướng dẫn giải:

Đáp án đúng là: D

Ta có bảng sau

Chiều cao trung bình

$\overline{x}=\frac{1}{500}\left(152.25+156.50+160.200+164.175+168.50\right)=\mathrm{161,4}$.

Phương sai của mẫu số liệu

$S^2=\frac{1}{500}\left({152}^2.25+{156}^2.50+{160}^2.200+{164}^2.175+{168}^2.50\right)-{\mathrm{161,4}}^2=\mathrm{14,84}$.

Độ lệch chuẩn $S=\sqrt{\mathrm{14,84}}\approx \mathrm{3,85}$.

Bài 2. Bảng dưới đây thống kê số tập bài chấm điểm thi vào 10 môn Toán tại TP Hà Nội năm 2024 tại một tổ chấm.

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là

A. 3,14;

B. 3,41;

C. 4,31;

D. 1,34.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có bảng sau

Cỡ mẫu n = 25.

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{\mathrm{1.1,5}+\mathrm{2.4,5}+\mathrm{4.7,5}+\mathrm{11.10,5}+\mathrm{7.13,5}}{25}=\mathrm{10,02}$.

Phương sai của mẫu số liệu ghép nhóm là

$S^2=\frac{{\mathrm{1.1,5}}^2+{\mathrm{2.4,5}}^2+{\mathrm{4.7,5}}^2+{\mathrm{11.10,5}}^2+{\mathrm{7.13,5}}^2}{25}-{\mathrm{10,02}}^2\approx \mathrm{9,85}$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S=\sqrt{\mathrm{9,85}}\approx \mathrm{3,14}$.

Bài 3. Theo kết quả thống kê điểm thi giữa kì 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là S² = 0,573. Độ lệch chuẩn của bảng thống kê đó bằng.

A. 0,936;

B. 0,757;

C. 0,812;

D. 0,657.

Hướng dẫn giải:

Đáp án đúng là: B

Độ lệch chuẩn $S=\sqrt{\mathrm{0,573}}\approx \mathrm{0,757}$.

Bài 4. Khảo sát về độ ẩm không khí trung bình các tháng năm 2022 tại Đà Nẵng (đơn vị: %), người ta được một mẫu dữ liệu ghép nhóm như sau:

Phương sai của mẫu số liệu ghép nhóm trên là

A. 11,1875;

B. 3,34;

C. 80,25;

D. 134,25.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có bảng có giá trị đại diện

Ta có $\overline{x}=\frac{\mathrm{1.72,5}+\mathrm{1.75,5}+\mathrm{2.78,5}+\mathrm{6.81,5}+\mathrm{2.84,5}}{12}=\mathrm{80,25}$.

Phương sai: $S^2=\frac{{\mathrm{1.72,5}}^2+{\mathrm{1.75,5}}^2+{\mathrm{2.78,5}}^2+{\mathrm{6.81,5}}^2+{\mathrm{2.84,5}}^2}{12}-{\mathrm{80,25}}^2=\mathrm{11,1875}$.

Bài 5. Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A. 11,62;

B. 0,36;

C. 3,41;

D. 0,017.

Hướng dẫn giải:

Đáp án đúng là: B

Ta có bảng có giá trị đại diện

Cỡ mẫu n = 20.

Ta có $\overline{x}=\frac{\mathrm{3.2,85}+\mathrm{6.3,15}+\mathrm{5.3,45}+\mathrm{4.3,75}+\mathrm{2.4,05}}{20}=\mathrm{3,39}$.

Phương sai: $S^2=\frac{{\mathrm{3.2,85}}^2+{\mathrm{6.3,15}}^2+{\mathrm{5.3,45}}^2+{\mathrm{4.3,75}}^2+{\mathrm{2.4,05}}^2}{20}-{\mathrm{3,39}}^2=\mathrm{0,1314}$.

Độ lệch chuẩn: $S=\sqrt{\mathrm{0,1314}}\approx \mathrm{0,36}$.

Bài 6. Hai mẫu số liệu ghép nhóm M₁; M₂ có bảng tần số ghép nhóm như sau:

M₁:

M₂:

Gọi s₁², s₂² lần lượt là phương sai của mẫu số liệu ghép nhóm M₁; M₂. Phát biểu nào sau đây là đúng?

A. s₁² =  2s₂² ;

B. $s_1^2=\frac{15}{8}{s}_2^2$;

C. $s_1^2=\frac{9}{5}{s}_2^2$;

D. 3s₁² =  s₂² .

Hướng dẫn giải:

Đáp án đúng là: B

Xét mẫu số liệu ghép nhóm M₁

Cỡ mẫu n = 30.

Có $\overline{x}=\frac{1.1+2.3+10.5+15.7+2.9}{30}=6$.

Phương sai $s_1^2=\frac{{1.1}^2+{2.3}^2+{10.5}^2+{15.7}^2+{2.9}^2}{30}-6^2=\frac{43}{15}$.

Mẫu số liệu ghép nhóm M₂

Cỡ mẫu n = 30.

Có $\overline{x}=\frac{0.1+1.3+15.5+13.7+1.9}{30}=\frac{89}{15}$.

Phương sai $s_2^2=\frac{{0.1}^2+{1.3}^2+{15.5}^2+{13.7}^2+{1.9}^2}{30}-{\left(\frac{89}{15}\right)}^2=\frac{344}{225}$.

Suy ra $s_1^2=\frac{15}{8}{s}_2^2$.

Bài 7. Để đánh giá chất lượng của một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn đến 4 chữ số thập phân).

A. 0,4252;

B. 0,5314;

C. 0,6214;

D. 0,5268.

Hướng dẫn giải:

Đáp án đúng là: D

Có $\overline{x}=\frac{\mathrm{2.5,25}+\mathrm{8.5,75}+\mathrm{15.6,25}+\mathrm{10.6,75}+\mathrm{5.7,25}}{40}=\mathrm{6,35}$.

Phương sai của mẫu số liệu ghép nhóm:

$s^2=\frac{{\mathrm{2.5,25}}^2+{\mathrm{8.5,75}}^2+{\mathrm{15.6,25}}^2+{\mathrm{10.6,75}}^2+{\mathrm{5.7,25}}^2}{40}-{\mathrm{6,35}}^2=\mathrm{0,2775}$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là $s=\sqrt{\mathrm{0,2775}}\approx \mathrm{0,5268}$.

Bài 8. Ở cuộc thi nhảy cao của học sinh 12. Kết quả được thống kê như sau

Giá trị phương sai về độ cao bằng

A. 26,14;

B. 18,04;

C. 26,41;

D. 26,9.

Hướng dẫn giải:

Đáp án đúng là: C

Ta có bảng có giá trị đại diện

Cỡ mẫu n = 42.

Có $\overline{x}=\frac{15.162+10.166+8.170+6.174+3.178}{42}=\frac{502}{3}$.

Phương sai:

$s^2=\frac{{15.162}^2+{10.166}^2+{8.170}^2+{6.174}^2+{3.178}^2}{42}-{\left(\frac{502}{3}\right)}^2=\frac{1664}{63}\approx \mathrm{26,41}$.

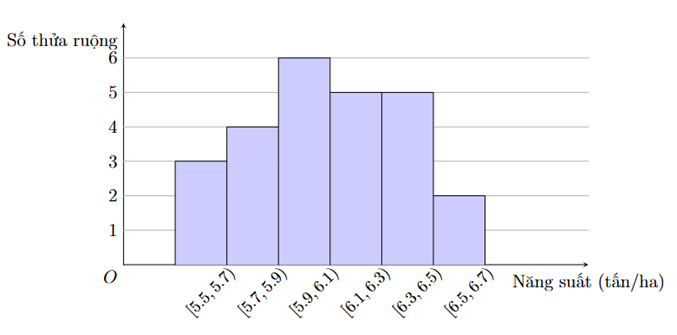
Bài 9. Kết quả khảo sát năng suất (đơn vị tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau

Độ lệch chuẩn của mẫu số liệu trên gần với giá trị nào nhất?

A. 0,294;

B. 0,301;

C. 0,289;

D. 0,086.

Hướng dẫn giải:

Đáp án đúng là: A

Dựa vào biểu đồ ta có bảng sau

Cỡ mẫu n = 25

Ta có $\overline{x}=\frac{\mathrm{3.5,6}+\mathrm{4.5,8}+\mathrm{6.6,0}+\mathrm{5.6,2}+\mathrm{5.6,4}+\mathrm{2.6,6}}{25}=\frac{761}{125}$.

Phương sai $s^2=\frac{{\mathrm{3.5,6}}^2+{\mathrm{4.5,8}}^2+{\mathrm{6.6,0}}^2+{\mathrm{5.6,2}}^2+{\mathrm{5.6,4}}^2+{\mathrm{2.6,6}}^2}{25}-{\left(\frac{761}{125}\right)}^2=\frac{1354}{15625}$.

Độ lệch chuẩn $s=\sqrt{\frac{1354}{15625}}\approx \mathrm{0,294}$.

Bài 10. Thống kê lợi nhuận hàng tháng (đơn vị: triệu đồng) trong 20 tháng của hai nhà đầu tư được cho như sau:

Lợi nhuận theo tháng của nhà đầu tư nhỏ

Lợi nhuận theo tháng của nhà đầu tư lớn

Chọn câu đúng nhất?

A. Không nên chỉ dựa vào độ lệch chuẩn để đánh giá mức độ rủi ro;

B. Lợi nhuận trung bình mỗi tháng của nhà đầu tư nhỏ cao hơn nhà đầu tư lớn;

C. Độ lệch chuẩn của nhà đầu tư lớn cao hơn 14;

D. Nhà đầu tư lớn có mức độ rủi ro cao hơn.

Hướng dẫn giải:

Đáp án đúng là: A

Lợi nhuận theo tháng của nhà đầu tư nhỏ có giá trị đại diện

Cỡ mẫu n = 20

Có ${\overline{x}}_A=\frac{2.15+4.25+8.35+4.45+2.55}{20}=35$.

Phương sai $S_A^2=\frac{{2.15}^2+{4.25}^2+{8.35}^2+{4.45}^2+{2.55}^2}{20}-{35}^2=120$.

Độ lệch chuẩn $S_A=\sqrt{120}\approx \mathrm{10,95}$.

Lợi nhuận theo tháng của nhà đầu tư lớn có giá trị đại diện

Cỡ mẫu n = 20

Có $\overline{x_B}=\frac{4.515+3.525+6.535+3.545+4.555}{20}=535$.

Phương sai $S_B^2=\frac{{4.515}^2+{3.525}^2+{6.535}^2+{3.545}^2+{4.555}^2}{20}-{535}^2=190$.

Độ lệch chuẩn $S_B=\sqrt{190}\approx \mathrm{13,78}$.

Độ lệch chuẩn cho lợi nhuận hàng tháng của nhà đầu tư lớn cao hơn của nhà đầu tư nhỏ. Lợi nhuận trung bình của hai nhà đầu tư khác nhau rất nhiều, do đó ta không nên dùng độ lệch chuẩn để so sánh mức độ rủi ro của hai nhà đầu tư này.

Xem thêm các dạng bài tập Toán 12 hay, chi tiết khác:

• Áp dụng định nghĩa và tính chất nguyên hàm
• Nguyên hàm của hàm số lũy thừa
• Nguyên hàm của hàm số lượng giác
• Nguyên hàm của hàm số mũ
• Nguyên hàm có điều kiện

---