Vận dụng tọa độ của vectơ để giải các bài toán thực tế lớp 12 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Vận dụng tọa độ của vectơ để giải các bài toán thực tế lớp 12 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Vận dụng tọa độ của vectơ để giải các bài toán thực tế.

Vận dụng tọa độ của vectơ để giải các bài toán thực tế lớp 12 (cách giải + bài tập)

1. Phương pháp giải

Vận dụng linh hoạt kiến thức biểu thức tọa độ vectơ, tích vô hướng, …vào giải quyết các bài toán thực tiễn.

2. Ví dụ minh họa

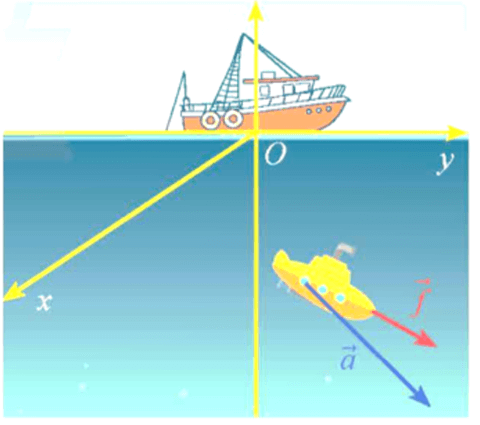
Ví dụ 1. Một thiết bị thăm dò đáy biển như hình vẽ được đẩy bởi một lực $\overrightarrow{f}=\left(5;4;-2\right)$ (đơn vị: N) giúp thiệt bị thực hiện độ dời $\overrightarrow{a}=\left(70;20;-40\right)$ (đơn vị: m). Tính công sinh bởi lực $\overrightarrow{f}$.

Hướng dẫn giải:

Công sinh bởi lực $\overrightarrow{f}$ là A = $\overrightarrow{f}.\overrightarrow{a}$ = 5.70 + 4.20 - 2.(-40) = 510J.

Ví dụ 2. Cho biết máy bay A đang bay với vectơ vận tốc $\overrightarrow{a}=\left(300;200;400\right)$ (đơn vị: km/h). Máy bay B bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay A. Tính tốc độ của máy bay B.

Hướng dẫn giải:

Theo đề ta có $\overrightarrow{b}=3\overrightarrow{a}$ ⇔ $\left\{\begin{array}{l}x=3.300\\ y=3.200\\ z=3.400\end{array}\right.$ ⇔ $\left\{\begin{array}{l}x=900\\ y=600\\ z=1200\end{array}\right.$ => $\overrightarrow{b}=\left(900;600;1200\right)$.

Tốc độ của máy bay B là $\left|\overrightarrow{b}\right|=\sqrt{{900}^2+{600}^2+{1200}^2}\approx \mathrm{1615,55}$(km/h).

3. Bài tập tự luyện

Bài 1. Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời. Đơn vị đo trong không gian Oxyz lấy theo km. Một chiếc ra đa đặt tại giàn khoan và một chiếc tàu thám hiểm có tọa độ là (30; 20; −15). Khoảng cách theo đơn vị km từ chiếc ra đa và một chiếc tàu thám hiểm (kết quả làm tròn lấy một chữ số thập phân).

A. 41,8 km;

B. 31,8 km;

C. 41,9 km;

D. 31,9 km.

Hướng dẫn giải:

Đáp án đúng là: A

Theo đề bài ta có tọa độ của ra đa là (0; 0; 0), tọa độ của tàu thám hiểm là (30; 25; −15).

Khi đó khoảng cách giữa ra đa và tàu thám hiểm là:

d = $\sqrt{{\left(30-0\right)}^2+{\left(25-0\right)}^2+{\left(-15-0\right)}^2}=5\sqrt{70}\approx \mathrm{41,8}$.

Vậy khoảng cách giữa ra đa và tàu thám hiểm là 41,8 km.

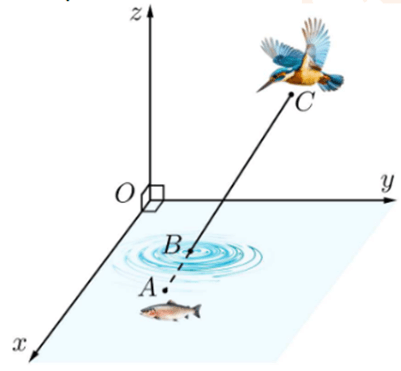
Bài 2. Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, trục Oz hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 2 m, cách mặt phẳng (Oxz), (Oyz) lần lượt là 3m và 1m phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 50 cm, cách mặt phẳng (Oxz), (Oyz) lần lượt là 1m và 1,5m. Tìm tọa độ điểm B lúc chim bói cá vừa tiếp xúc với mặt nước.

A. $\left(\frac{7}{5};\frac{7}{5};0\right)$;

B. $\left(\frac{7}{5};0;0\right)$;

C. $\left(\frac{7}{5};0;\frac{7}{5}\right)$;

D. $\left(0;\frac{7}{5};\frac{7}{5}\right)$.

Hướng dẫn giải:

Đáp án đúng là: A

Theo đề ta có A(1,5; 1; −0,5); C(1; 3; 2); $\overrightarrow{AC}=\left(-\mathrm{0,5};2;\mathrm{2,5}\right)$.

Gọi B(x; y; 0) => $\overrightarrow{AB}=\left(x-\mathrm{1,5};y-1;\mathrm{0,5}\right)$.

Vì $\overrightarrow{AB},\overrightarrow{AC}$ cùng phương nên $\frac{x-\mathrm{1,5}}{-\mathrm{0,5}}=\frac{y-1}{2}=\frac{\mathrm{0,5}}{\mathrm{2,5}}=\frac{1}{5}$ => $\left\{\begin{array}{l}x=\frac{7}{5}\\ y=\frac{7}{5}\end{array}\right.$.

Vậy $B\left(\frac{7}{5};\frac{7}{5};0\right)$.

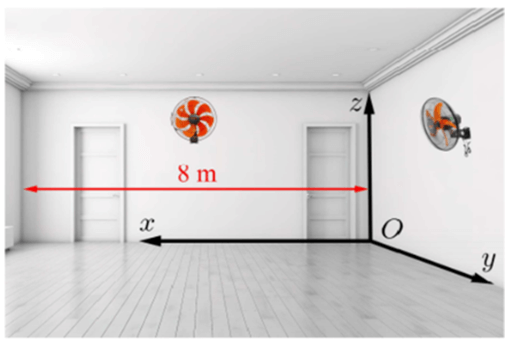
Bài 3. Một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, chiều rộng 6m và cao 4m có hai chiếc quạt treo tường. Chiếc quạt A treo chính giữa bức tường 8m và cách trần 1m, chiếc quạt B treo chính giữa bức tường 6m và cách trần 1,5m. Hỏi khoảng cách giữa hai chiếc quạt AB cách nhau bao nhiêu m (làm tròn đến hàng phần nghìn).

A. 25,25;

B. 5,205;

C. 5,502;

D. 5,025.

Hướng dẫn giải:

Đáp án đúng là: D

Chọn hệ trục tọa độ như hình vẽ, khi đó ta có điểm A(4; 0; 3) và điểm $B\left(0;3;\frac{5}{2}\right)$

Suy ra $\overrightarrow{AB}=\left(-4;3;-\frac{1}{2}\right)$. Do đó độ dài đoạn thẳng AB = 5,025.

Bài 4. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy bằng km, ra đa phát hiện một máy bay chiến đấu X di chuyển với vận tốc và hướng không đổi từ điểm M(1000; 600; 4) đến điểm N trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 30 phút tiếp theo là Q(1400; 800; 16). Tính quãng đường máy bay đi được sau 30 phút kể từ lúc ra đa phát hiện (làm tròn đến hàng đơn vị).

A. 224 km;

B. 242 km;

C. 448 km;

D. 484 km.

Hướng dẫn giải:

Đáp án đúng là: A

Quãng đường mà máy bay bay được sau 30 phút kể từ lúc ra đa phát hiện là:

$\frac{1}{2}MQ=\frac{1}{2}\sqrt{{\left(1400-1000\right)}^2+{\left(800-600\right)}^2+{\left(16-4\right)}^2}\approx 224$ km.

Bài 5. Trong không gian với một hệ trục tọa độ Oxyz cho trước (đơn vị đo lấy theo mét), một công ty xây dựng cần xác định chiều dài của một sợi dây cáp nối giữa hai điểm cao trên hai toàn nhà để lắp đặt hệ thống điện. Tòa nhà thứ nhất có đỉnh ở vị trí A(3; 5; 12) và tòa nhà thứ hai có đỉnh ở vị trí B(8; 2; 20). Hỏi công ty cần chuẩn bị sợi dây cáp có chiều dài tối thiểu là bao nhiêu mét để nối hai đỉnh tòa nhà (làm tròn đến hàng đơn vị).

A. 12;

B. 11;

C. 10;

D. 9.

Hướng dẫn giải:

Đáp án đúng là: C

Ta có $\overrightarrow{AB}=\left(5;-3;8\right)$ => AB = $\sqrt{5^2+{\left(-3\right)}^2+8^2}\approx 10$.

Vậy dây cáp có chiều dài tối thiểu là 10 mét.

Bài 6. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy theo km, một ra đa phát hiện một máy bay di chuyển với vận tốc và hướng không đổi từ điểm M(1000; 600; 14) đến điểm N(a; b; c) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 10 phút tiếp theo máy bay đến vị trí điểm Q(1400; 800; 18). Tính a + b + c.

A. 2760;

B. 2076;

C. 2706;

D. 2067.

Hướng dẫn giải:

Đáp án đúng là: D

Theo đề ta có $\overrightarrow{MN}=\frac{3}{4}\overrightarrow{MQ}$ ⇔ $\left\{\begin{array}{l}a-1000=\frac{3}{4}\left(1400-1000\right)\\ b-600=\frac{3}{4}\left(800-600\right)\\ c-14=\frac{3}{4}\left(18-14\right)\end{array}\right.$

⇔ $\left\{\begin{array}{l}a=1300\\ b=750\\ c=17\end{array}\right.$.

Do đó a + b + c = 2067.

Bài 7. Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân với điểm đặt S(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A(−2; 0; 0), $B\left(1;\sqrt{3};0\right)$, $C\left(1;-\sqrt{3};0\right)$. Biết rằng trọng lực tác dụng lên chiếc máy có độ lớn là 30 N và được phân bố thành ba lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ có độ lớn bằng nhau như hình dưới. Tính tích vô hướng của $\overrightarrow{F_1}.\overrightarrow{F_2}$.

A. 7,85;

B. 78,5;

C. 85,7;

D. 87,5.

Hướng dẫn giải:

Đáp án đúng là: D

Ta có $\overrightarrow{SA}=\left(-2;0;-4\right)$, $\overrightarrow{SB}=\left(1;\sqrt{3};-4\right),\overrightarrow{SC}=\left(1;-\sqrt{3};4\right)$ => SA = SB = SC = $\sqrt{20}$.

Lại có $\overrightarrow{AB}=\left(3;\sqrt{3};0\right)$, $\overrightarrow{AC}=\left(3;-\sqrt{3};0\right)$, $\overrightarrow{BC}=\left(0;-2\sqrt{3};0\right)$ => AB = AC = BC = $\sqrt{12}$.

Suy ra hình chóp S.ABC đều có đường cao là SO = 4 với O(0; 0; 0) là trọng tâm tam giác ABC.

Mặt khác $\overrightarrow{F_1}=k\overrightarrow{SA}=\left(-2k;0;-4k\right)$, $\overrightarrow{F_2}=k\overrightarrow{SB}=\left(k;\sqrt{3}k;-4k\right)$,

$\overrightarrow{F_3}=k\overrightarrow{SC}=\left(k;-\sqrt{3}k;-4k\right)$ => $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;-12k\right)$

Mà $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{P}=\left(0;0;-30\right)$ nên −12k = −30 ⇔ $k=\frac{5}{2}$.

Suy ra $\overrightarrow{F_1}=\left(-5;0;-10\right)$, $\overrightarrow{F_2}=\left(\frac{5}{2};\frac{5\sqrt{3}}{2};-10\right)$. Vậy $\overrightarrow{F_1}\cdot \overrightarrow{F_2}=\frac{175}{2}=\mathrm{87,5}$.

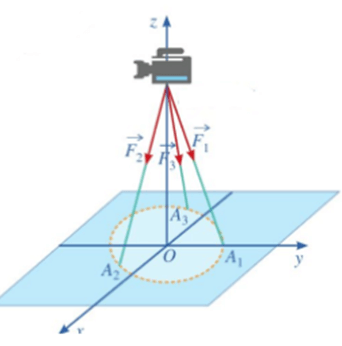
Bài 8. Một chiếc máy ảnh được đặt trên giá đỡ ba chân với điểm đặt E(0; 0; 8) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A₁(0; 1; 0), $A_2\left(\frac{\sqrt{3}}{2};-\frac{1}{2};0\right)$, $A_3\left(\frac{-\sqrt{3}}{2};-\frac{1}{2};0\right)$.

Biết rằng trọng lượng của chiếc máy là 240N. Tọa độ của các lực tác dụng lên giá đỡ $\overrightarrow{F_1}$ là

A. $\overrightarrow{F_1}=\left(0;10;-80\right)$;

B. $\overrightarrow{F_1}=\left(0;10;80\right)$;

C. $\overrightarrow{F_1}=\left(0;-10;-80\right)$;

D. $\overrightarrow{F_1}=\left(10;0;-80\right)$.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có $\overrightarrow{E{A}_1}=\left(0;1;-8\right)$, $\overrightarrow{E{A}_2}=\left(\frac{\sqrt{3}}{2};-\frac{1}{2};-8\right)$, $\overrightarrow{E{A}_3}=\left(\frac{-\sqrt{3}}{2};-\frac{1}{2};-8\right)$

Nên $E{A}_1=E{A}_2=E{A}_3=\sqrt{65}$.

Mặt khác $\left|\overrightarrow{F_1}\right|=\left|\overrightarrow{F_2}\right|=\left|\overrightarrow{F_3}\right|$ vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ.

Do đó $\overrightarrow{F_1}=k\overrightarrow{E{A}_1}=\left(0;k;-8k\right)$, $\overrightarrow{F_2}=k\overrightarrow{E{A}_2}=\left(\frac{\sqrt{3}}{2}k;-\frac{1}{2}k;-8k\right)$,

$\overrightarrow{F_3}=k\overrightarrow{E{A}_3}=\left(-\frac{\sqrt{3}}{2}k;-\frac{1}{2}k;-8k\right)$ => $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;-24k\right)$

Mà $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{P}=\left(0;0;-240\right)$ => −24k = −240 => k =10.

Vậy $\overrightarrow{F_1}=\left(0;10;-80\right)$.

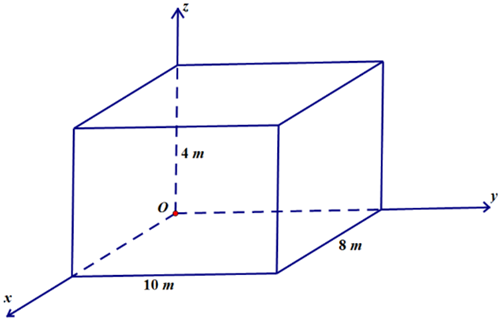
Bài 9. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 8 m và chiều cao là 4 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét.

Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm).

A. 57;

B. 7,55;

C. 75,5;

D. 5,75.

Hướng dẫn giải:

Đáp án đúng là: B

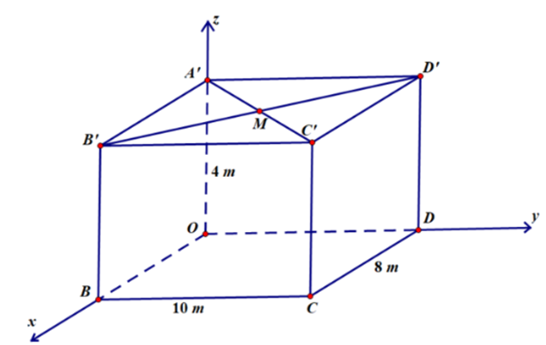
Với hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét.

Phòng học thiết kế dạng hình hộp chữ nhật OBCD. A'B'C'D' với A'B'C'D' là hình chữ nhật.

Gọi M là giao điểm của hai đường chéo A'C' và B'D' nên M là trung điểm của A'C' với A'(0; 0; 4), C'(8; 10; 4).

Vì đèn được treo lại chính giữa trần nhà của phòng học nên điểm treo bóng đèn trùng với điểm M.

Ta có $\left\{\begin{array}{l}{x}_M=\frac{x_{A^{\text{'}}}+x_{C^{\text{'}}}}{2}=4\\ y_M=\frac{y_{A^{\text{'}}}+y_{C^{\text{'}}}}{2}=5\\ z_M=\frac{z_{A^{\text{'}}}+z_{C^{\text{'}}}}{2}=4\end{array}\right.$ nên M(4; 5; 4).

Vậy khoảng cách từ điểm treo bóng đèn đến góc phòng học là $OM=\sqrt{4^2+5^2+4^2}=\sqrt{57}\approx \mathrm{7,55}$.

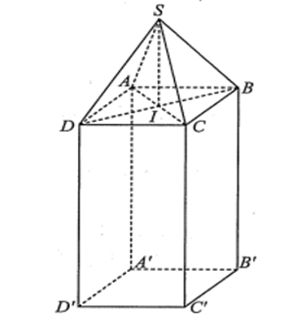
Bài 10. Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp tứ giác đều S.ABCD và đặt lên phía trên một trụ hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông (như hình vẽ bên).

Chọn hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là mét) sao cho A'(0; 0; 0), A(0; 0; 1), $B\left(0;\frac{1}{2};1\right)$. Biết rằng, ban tổ chức sự kiện dự định dùng các tấm kính cường lực hình tam giác cân có cạnh bên là 60 cm để ráp lại thành khối chóp nói trên. Khi đó, tọa độ điểm S(a; b; c). Tính giá trị của a + b + c (làm tròn kết quả đến hàng phần trăm).

A. 0,98;

B. 0,89;

C. 1,98;

D. 1,89.

Hướng dẫn giải:

Đáp án đúng là: C

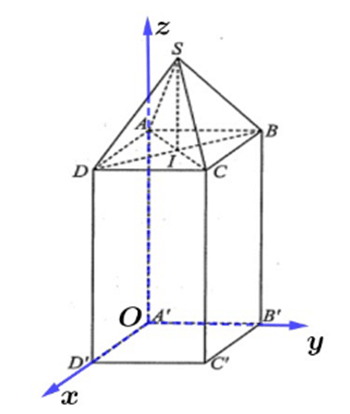
Chọn hệ trục tọa độ Oxyz như hình vẽ

Do giả thiết khối chóp tứ giác đều S.ABCD nên ABCD là hình vuông.

Có A'(0; 0; 0), A(0; 0; 1), $B\left(0;\frac{1}{2};1\right)$, $B^{\text{'}}\left(0;\frac{1}{2};0\right)$, $D^{\text{'}}\left(\frac{1}{2};0;0\right)$, $D\left(\frac{1}{2};0;1\right)$.

I là trung điểm của BD nên $I\left(\frac{1}{4};\frac{1}{4};1\right)$.

Ta có $BD=\frac{\sqrt{2}}{2}$; $IB=ID=\frac{\sqrt{2}}{4}$; $SI=\sqrt{S{B}^2-I{B}^2}=\sqrt{{\mathrm{0,6}}^2-{\left(\frac{\sqrt{2}}{4}\right)}^2}=\frac{\sqrt{94}}{20}$.

Vậy $S\left(\frac{1}{4};\frac{1}{4};\frac{\sqrt{94}}{20}+1\right)$. Suy ra a + b + c ≈ 1,98.

Xem thêm các dạng bài tập Toán 12 hay, chi tiết khác:

• Xác định khoảng biến thiên và ý nghĩa của khoảng biến thiên trong việc đo mức độ phân tán
• Xác định khoảng tứ phân vị và ý nghĩa của khoảng tứ phân vị trong việc đo mức độ phân tán
• Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và vận dụng đo mức độ rủi ro
• Áp dụng định nghĩa và tính chất nguyên hàm
• Nguyên hàm của hàm số lũy thừa

---