Các dạng bài tập Sóng ánh sáng có lời giải
Các dạng bài tập Sóng ánh sáng có lời giải
(199k) Xem Khóa học Vật Lí 12 KNTTXem Khóa học Vật Lí 12 CDXem Khóa học Vật Lí 12 CTST
Phần Sóng ánh sáng Vật Lí lớp 12 sẽ tổng hợp Lý thuyết, các dạng bài tập chọn lọc giúp ôn thi Tốt nghiệp môn Vật Lí và trên 400 bài tập trắc nghiệm có lời giải. Vào Xem chi tiết để theo dõi các dạng bài Sóng ánh sáng hay nhất tương ứng.
Tổng hợp Lý thuyết Chương Sóng ánh sáng
- Lý thuyết Tán sắc ánh sáng Xem chi tiết
- Lý thuyết Giao thoa ánh sáng Xem chi tiết
- Lý thuyết Các loại quang phổ Xem chi tiết
- Lý thuyết Tia hồng ngoại, tia tử ngoại, tia X. Thang sóng điện từ Xem chi tiết
Chủ đề: Tán sắc ánh sáng
- Dạng 1 : Bài tập Hiện tượng tán sắc ánh sáng ôn thi Tốt nghiệp (có lời giải) Xem chi tiết
40 bài tập trắc nghiệm Tán sắc qua lăng kính có lời giải (phần 1)
40 bài tập trắc nghiệm Tán sắc qua lăng kính có lời giải (phần 2)
Chủ đề: Giao thoa ánh sáng
- Dạng 2 : Bài tập Hiện tượng giao thoa ánh sáng ôn thi Tốt nghiệp (có lời giải) Xem chi tiết
50 bài tập trắc nghiệm Giao thoa ánh sáng có lời giải (phần 1)
50 bài tập trắc nghiệm Giao thoa ánh sáng có lời giải (phần 2)
Chủ đề: Quang Phổ
- Dạng 3 : Bài tập Quang phổ ôn thi Tốt nghiệp (có lời giải) Xem chi tiết
Bài tập trắc nghiệm Sóng ánh sáng
100 câu trắc nghiệm Sóng ánh sáng có lời giải (cơ bản - phần 1)
100 câu trắc nghiệm Sóng ánh sáng có lời giải (cơ bản - phần 2)
100 câu trắc nghiệm Sóng ánh sáng có lời giải (cơ bản - phần 3)
100 câu trắc nghiệm Sóng ánh sáng có lời giải (nâng cao - phần 1)
100 câu trắc nghiệm Sóng ánh sáng có lời giải (nâng cao - phần 2)
100 câu trắc nghiệm Sóng ánh sáng có lời giải (nâng cao - phần 3)
Cách giải bài tập Tán sắc qua lăng kính
1. Phương pháp
+ Áp dụng các công thức của lăng kính:
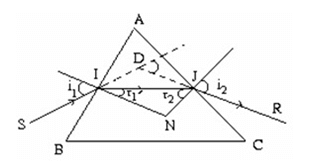
sini1 = nsinr1; sini2 = nsinr2;
A = r1 + r2; D = i2 + i2 - A.
Khi i1 = i2 (r1 = r2) thì D = Dmin với
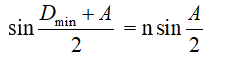
+ Trường hợp góc chiết quang A và góc tới i1 đều nhỏ (≤ 100), ta có các công thức gần đúng: i1 = nr1; i2 = nr2; A = r1 + r2; D = (n – 1)A; Dmin = A(n – 1).
Trong một số trường hợp khác, ta cần giải một số bài toán liên quan đến định luật phản xạ: i = i’, định luật khúc xạ: n1sini1 = n2sini2.
2. Ví dụ
Ví dụ 1: Bước sóng của ánh sáng đỏ trong không khí là 0,64 μm . Tính bước sóng của ánh sáng đó trong nước biết chiết suất của nước đối với ánh sáng đỏ là 4/3 .
Lời giải:
Ta có:
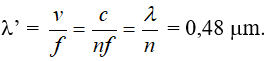
Ví dụ 2: Một chùm ánh sáng hẹp, đơn sắc có bước sóng trong chân không là λ = 0,60 μm. Xác định chu kì, tần số của ánh sáng đó. Tính tốc độ và bước sóng của ánh sáng đó khi truyền trong thủy tinh có chiết suất n = 1,5.
Lời giải:
Ta có
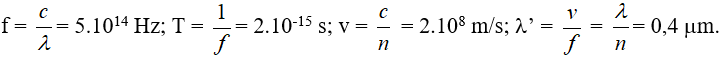
Ví dụ 3: Một lăng kính có góc chiết quang là 60ο. Biết chiết suất của lăng kính đối với ánh sáng đỏ là 1,5. Chiếu tia sáng màu đỏ vào mặt bên của lăng kính với góc tới 60ο. Tính góc lệch của tia ló so với tia tới.
Ta có:
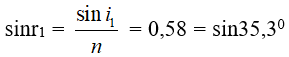
⇒ r1 = 35,3ο ⇒ r2 = A – r1 = 24,7ο; sini2 = nsinr2 = 0,63 = sin38,0ο
⇒ i2 = 38,8ο ⇒ D = i2 + i2 – A = 38,8ο.
Cách giải bài tập Giao thoa với ánh sáng đơn sắc
A. Phương pháp & Ví dụ
Dạng 1.1. Vị trí vân sáng, vân tối - khoảng vân
a- Khoảng vân: là khoảng cách giữa 2 vân sáng liền kề
i = λD / a ( i phụ thuộc λ ⇒ khoảng vân của các ánh sáng đơn sắc khác nhau là khác nhau với cùng một thí nghiệm).
b- Vị trí vân sáng bậc k: Tại đó ứng với Δd = d2 – d1 = k.λ , đồng thời 2 sóng ánh sáng truyền tới cùng pha
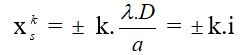
Để A là vân sáng trung tâm thì
k = 0 hay d = 0
k = 0: ứng với vân sáng trung tâm
k = 1: ứng với vân sáng bậc 1
…………
k = n: ứng với vân sáng bậc n.
c- Vị trí vân tối thứ k + 1: Tại đó ứng với Δd = (k + 0,5 ).λ . Là vị trí hai sóng ánh sáng truyền tới ngược pha nhau.
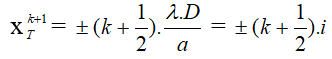
Hay vân tối thứ k:
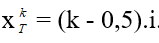
Ví dụ
Vị trí vân sáng bậc 5 là:
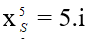
Vị trí vân tối thứ 4:
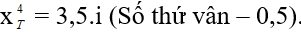
Dạng 1.2. Khoảng cách giữa các vân
Loại 1- Khoảng cách vân cùng bản chất liên tiếp: l = (số vân – 1).i
Ví dụ: khoảng cách giữa 7 vân sáng liên tiếp: l = (7 – 1).i = 6i
Loại 2- Giữa một vân sáng và một vân tối bất kỳ:
Giả sử xét khoảng cách vân sáng bậc k và vân tối thứ k’, vị trí:
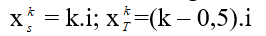
Nếu:
+ Hai vân cùng phía so với vân trung tâm:
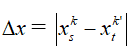
+ Hai vân khác phía so với vân trung tâm:
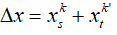
-Khoảng cách giữa vân sáng và vân tối liền kề là : i/2 nên vị trí vân tối các thứ liên tiếp được xác định: xt = ki / 2 (với k lẻ: 1,3,5,7,….)
VD: Tìm khoảng cách giữa vân sáng bậc 5 và vân tối thứ 6
Giải:
Ta có
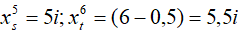
+ Nếu hai vân cùng phía so với vân trung tâm:
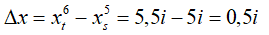
+ Nếu hai vân khac phía so với vân trung tâm :
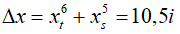
Loại 3- Xác định vị trí một điểm M bất kì trên trường giao thoa cách vân trung tâm một khoảng xM có vân sáng hay vân tối, bậc mấy ?
+ Lập tỉ số:
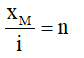
Nếu n nguyên, hay n ∈ Z, thì tại M có vân sáng bậc k=n.
Nếu n bán nguyên hay n = k + 0,5 với k Z, thì tại M có vân tối thứ k +1
Ví dụ
Ví dụ: Một khe hẹp F phát ánh sáng đơn sắc bước sóng λ = 600nm chiếu sáng hai khe song song với F và cách nhau 1m. Vân giao thoa được quan sát trên một màn M song song với màn phẳng chứa F1 và F2 và cách nó 3m. Tại vị trí cách vân trung tâm 6,3m có
A. Vân tối thứ 4 B. Vân sáng bậc 4 C. Vân tối thứ 3 D. Vân sáng bậc 3
Lời giải:
Ta cần xét tỉ số x / i
Khoảng vân i= λD / a = 1,8mm, ta thấy 6,3 / 1,8 = 3,5 là một số bán nguyên nên tại vị trí cách vân trung tâm 6,3mm là một vân tối
Mặt khác xt = (k + 0,5)i= 6,3 nên ( k+ 0,5 )=3,5 nên k= 3. Vậy tại vị trí cách vân trung tâm 6,3mm là một vân tối thứ 4 vậy chọn đáp án A
Dạng 1.3. Xác định số vân trên trường giao thoa
- Trường giao thoa xét là chiều rộng của khu vực chứa toàn bộ hiện tượng giao thoa hứng được trên màn- kí kiệu L.
- Số vân trên trường giao thoa:
+ Số vân sáng:
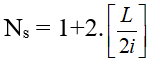
+ Số vân tối:
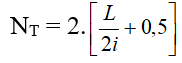
- Số vân sáng, vân tối trong đoạn MN, với 2 điểm M, N thuộc trường giao thoa nằm 2 bên vân sáng trung tâm:
+ Số vân sáng:
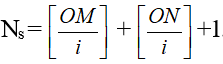
+ Số vân tối:
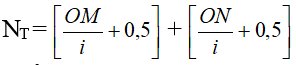
- Số vân sáng, tối giữa 2 điểm MN trong đoạn giao thoa nằm cùng phía so với vân sáng trung tâm:
+ Số vân sáng:
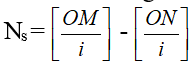
+ Số vân tối:
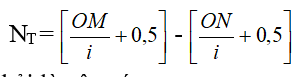
Với M, N không phải là vân sáng.
Ví dụ
Ví dụ: Trong một thí nghiệm về Giao thoa anhs sáng bằng khe I âng với ánh sáng đơn sắc λ = 0,7 μ m, khoảng cách giữa 2 khe s1,s2 là a = 0,35 mm, khoảng cách từ 2 khe đến màn quan sát là D = 1m, bề rộng của vùng có giao thoa là 13,5 mm. Số vân sáng, vân tối quan sát được trên màn là:
A: 7 vân sáng, 6 vân tối; B: 6 vân sáng, 7 vân tối.
C: 6 vân sáng, 6 vân tối; D: 7 vân sáng, 7 vân tối.
Lời giải:
Ta có khoảng vân
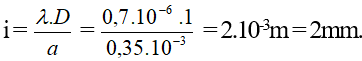
Số vân sáng:
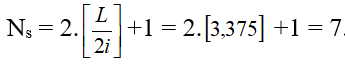
Do phân thập phân của L/2i là 0,375 < 0,5 nên số vạch tối là NT = Ns – 1 = 6 Số vạch tối là 6, số vạch sáng là 7. đáp án A.
Cách giải bài tập Giao thoa với ánh sáng đa sắc
A. Phương pháp & Ví dụ
Nhận xét
Khi cho chùm đa sắc gồm nhiều bức xạ chiếu vào khe Y-âng để tạo ra giao thoa. Trên màn quan sát được hệ vân giao thoa của các bức xạ trên. Vân trung tâm là sự chồng chập của các vân sáng bậc k = 0 của các bức xạ này. Trên màn thu được sự chồng chập: của các vạch sáng trùng nhau, các vạch tối trùng nhau hoặc vạch sáng trùng vạch tối giữa các bức xạ này.
Ta có: Giao thoa của hai hay nhiều bức xạ:
Dạng 2.1. Vị trí vân sáng trùng:
k1i1 = k2i2⇒...⇒k1 λ1 ⇒ k2 λ2
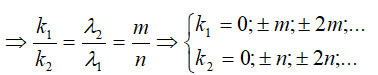
Hoặc ta có thể xác định:Vị trí vân sáng của các bức xạ đơn sắc trùng nhau
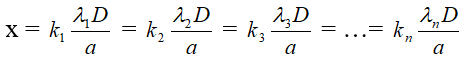
k1λ1 = k2λ2 = k3λ3 = k4λ4 = .... = knλn với k1, k2, k3,…, kn ∈ Z
Dựa vào phương trình biện luận chọn các giá trị k thích hợp, thông thường chọn k là bội số của số nguyên nào đó.
Ví dụ:
Hai bức xạ λ1 và λ2 cho vân sáng trùng nhau. Ta có k1λ1 = k2λ2 ⇒
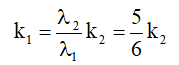
Vì k1, k2 là các số nguyên, nên ta chọn được k2 là bội của 6 và k1 là bội của 5
Có thể lập bảng như sau:
| k1 | 0 | 5 | 10 | 15 | 20 | 25 | ..... |
| k2 | 0 | 6 | 12 | 18 | 24 | 30 | ..... |
| x | 0 | ..... | ..... | ..... | ..... | ..... | ..... |
Dạng 2.2. Khoảng vân trùng
(khoảng cách nhỏ nhất giữa hai vân cùng màu với vân trung tâm):
i12 = mi1 = ni2 = ...
hoặc: i12 = BCNN(i1, i2)
Ba bức xạ: i12 = BCNN(i1, i2, i3)
Dạng 2.3. Xét cụ thể với chùm sáng gồm 2 bức xạ λ1, λ2
Loại 1: Vị trí hai vân sáng trùng nhau. Ngoài cách tổng quát trên ta có thể làm như sau:
+ Số vạch trùng quan sát được. Số vạch sáng quan sát được:
Khi có giao thoa: Vị trí vân sáng:
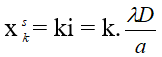
Khi 2 vân sáng của 2 bức xạ trùng nhau:
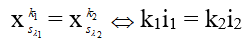
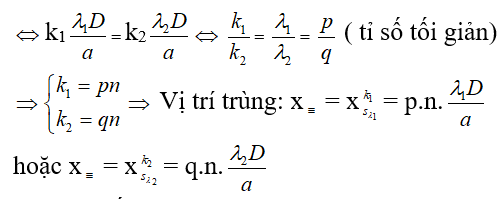
+ Số vạch trùng quan sát được trên trường giao thoa L:
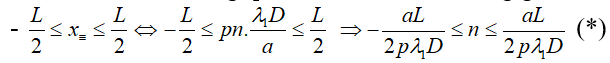
mỗi giá trị n → 1 giá trị k ⇒ số vạch sáng trùng là số giá trị n thỏa mãn (*).
+ Xét số vân trùng trên MN− ∈ L:
xM ≤ x ≡ ≤ xN (xM < xN; x là tọa độ) ⇒ khoảng n ⇒số giá trị n là số vân sáng trùng thuộc + Xét số vân trùng trên MN−.
Chú ý: Nếu M,N là vân sáng trùng ⇒ dùng dấu “ = „.
+ Số vạch quan sát được trên trường L:
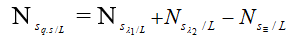
+ Số vạch quan sát được trên MN− L:
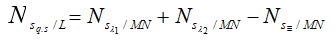
( Nhớ chú ý M,N có phải là vân sáng trùng không )
Ví dụ
Ví dụ : Trong thí nghiệm về giao thoa ánh sáng qua khe I-Âng có a= 2mm D=2m, nguồn sáng gồm hai bức xạ λ1 = 0,5μm, λ2 = 0,4μm. Tìm số vân sáng quan sát được trên trường giao thoa ?
Lời giải:
Ta có :
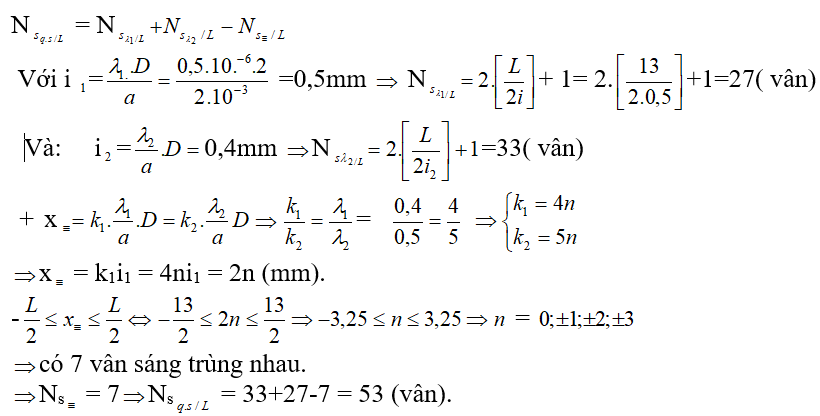
+ Bậc trùng nhau của từng bức xạ và vị trí trung nhau:
BT trên; Tìm khoảng cách giữa 2 vân sáng trùng nhau gần nhau nhất?
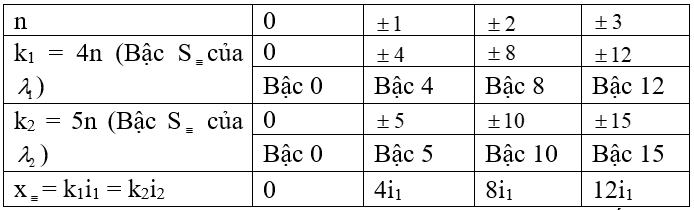
Nhận xét: Khoảng cách giữa 2 vân sáng trùng nhau liên tiếp là như nhau và là 4i1 hay 5i2.
Trong bài này là
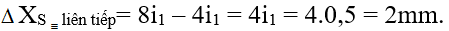
Loại 2: Hai vân tối trùng nhau của hai bức xạ:
- Khi vân tối của 2 bức xạ trùng nhau:
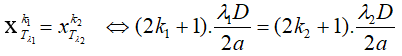

Vị trí trùng: x
xT≡ nằm trong vùng khảo sát:
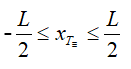
+ Số vân xT≡ trong trường giao thoa:
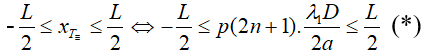
Số giá trị của n thỏa mãn (∗)⇒ số vân tối trùng trong trường giao thoa.
+ Số vân xT≡ trong miền MN−L:
xM ≤xT≡ ≤xN (xM; xN là tọa độ và xM < xN (∗∗)
Số vân tối trùng trong vùng MN− là số giá trị n thỏa mãn (∗∗)
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa I âng thực hiện đồng thời hai bức xạ đơn sắc với khoảng vân trên màn thu được lần lượt là: i1 = 0,5mm; i2 = 0,3mm. Biết bề rộng trường giao thoa là 5mm, số vị trí trên trường giao thoa có 2 vân tối của hai hệ trùng nhau là bao nhiêu?
Lời giải:
Khi 2 vân tối trùng nhau:
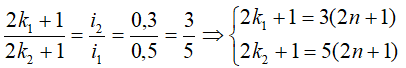
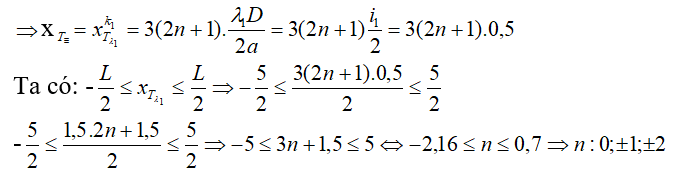
⇒có 4 vị trí vân tối trùng nhau trên trường giao thoa L.
Loại 3: Vân sáng của bức xạ này trùng vân tối của bức xạ kia.
- Giả sử:
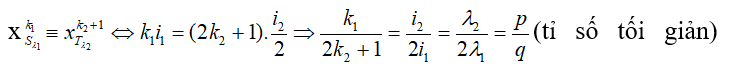
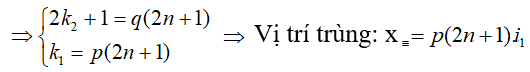
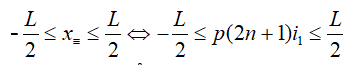
⇒số vân sáng trùng vân tối là số giá trị của n thỏa mãn biểu thức này
Chú ý: Có thể xét xTλ1 = xTλ2
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa I âng, thực hiện đồng thời với 2 ánh sáng đơn sắc khoảng vân giao thoa trên màn lần lượt i1 = 0,8mm, i2 = 0,6mm. Biết trường giao thoa rộng: L = 9,6mm. Hỏi số vị trí mà :
a) xTλ1 = xSλ2 . ( -2,5 ≤ n ≤ 1,5 : có 4 vị trí)
b) xSλ1 = xTλ2
Lời giải:
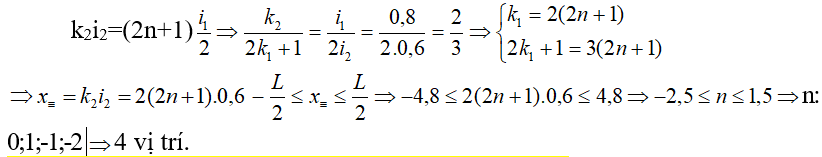
(199k) Xem Khóa học Vật Lí 12 KNTTXem Khóa học Vật Lí 12 CDXem Khóa học Vật Lí 12 CTST
Xem thêm các dạng bài tập Vật Lí lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:
- Dao động cơ
- Sóng cơ và Sóng âm
- Dòng điện xoay chiều
- Dao động và Sóng điện từ
- Lượng tử ánh sáng
- Hạt nhân nguyên tử
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

