Giáo án Toán 10 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác (mới, chuẩn nhất)
Giáo án Toán 10 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Chỉ từ 300k mua trọn bộ Kế hoạch bài dạy (KHBD) hay Giáo án Toán 10 cả năm (mỗi bộ sách) bản word chuẩn kiến thức, trình bày đẹp mắt:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
A. KẾ HOẠCH CHUNG
Phân phối thời gian |
Tiến trình dạy học |
||
Tiết 1 |
HOẠT ĐỘNG KHỞI ĐỘNG (giới thiệu) |
||
HOẠT ĐỘNG ÔN TẬP KIẾN THỨC |
Định lý Cô sin |
||
Tiết 2 |
Định lý Sin |
||
Công thức diện tích |
|||
Tiết 3 |
Giải tam giác và ứng dụng vào việc đo đạc |
||
Tiết 4 |
HOẠT ĐỘNG KHỞI ĐỘNG (giới thiệu) |
||
B. KẾ HOẠCH DẠY HỌC
I. MỤC TIÊU CỦA BÀI:
Qua bài học này học sinh phải đạt được những kiến thức tối thiểu sau.
1. Kiến thức:
- Các hệ thức lượng trong tam giác vuông, định lí hàm số cosin, định lí hàm số sin, các công thức tính diện tích của tam giác, từ đó biết áp dụng vào giải tam giác và ứng dụng vào thực tế đo đạc.
2. Kỹ năng. Học sinh biết
- Áp dụng định lí côsin, định lí sin, công thức về độ dài đường trung tuyến, các công thức tính diện tích để giải một số bài toán liên quan đến tam giác.
- Giải tam giác trong một số trường hợp đơn giản. Biết vận dụng giải tam giác vào các bài toán có nội dung thực tiễn. Kết hợp với việc sử dụng máy tính bỏ túi khi giải toán.
3. Về thái độ. Học sinh nắm công thức từ đó biết liên hệ toán học vào thực tế.
4. Định hướng phát triển năng lực.
Năng lực tự học, năng lực hợp tác, năng lực giao tiếp, năng lực quan sát, năng lực phát hiện và giải quyết vấn đề, năng lực tính toán, năng lực vận dụng kiến thức vào cuộc sống ...
II. Chuẩn bị của giáo viên và học sinh.
1. Giáo viên.
- Giáo án, phấn màu, thước.
- Phiếu học tập.
2. Học sinh.
- Xem lại các hệ thức lượng đã học.
III. Chuỗi các hoạt động học.
1. Giới thiệu.
Câu 1. Người ta muốn đo chiều cao của tháp Eiffel (ở hình 1) mà không thể trèo lên đỉnh của nó mà kéo thước dây để đo trực tiếp được. Em hãy giúp họ đo chiều cao của tháp Eiffel?
Câu 2. Làm sao để đo chiều cao của cây (ở hình 2) mà ta không thể trèo lên đến đỉnh của nó để đo trực tiếp được?
Câu 3. Tính khoảng cách từ vị trí A đến vị trí C ở giữa hồ Gươm (ở hình 3) mà ta không thể trực tiếp đến để đo được.
Câu 4. Khi khai quật một ngôi mộ cổ, người ta tìm được một mảnh của 1 chiếc đĩa phẳng hình tròn bị vỡ (hình 4). Dựa vào các tài liệu đã có, các nhà khảo cổ đã biết hình vẽ trên phần còn lại của chiếc đĩa. Họ muốn làm một chiếc đĩa mới phỏng theo chiếc đĩa này. Em hãy giúp họ tìm bán kính chiếc đĩa.
2. Nội dung bài học.
2.1 Định lí Côsin.
a) Tiếp cận định lí.
Hoạt động 1.
|
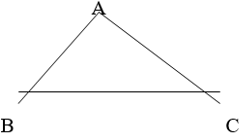
Bài toán. Trong tam giác ABC cho biết hai cạnh AB,AC và góc A. Hãy tính cạnh BC. |
Giải. Ta có: |
Định lí côsin.
|
Trong tam giác ABC bất kì với BC=a,CA=b,AB=c ta có: a2=b2+c2-2bc.cosA b2=a2+c2-2ac.cosB c2=a2+b2-2ab.cosC |
Củng cố định lí.
|
Ví dụ 1. Cho tam giác ABC có cạnh b=8 , cạnh c=6 và góc |
Gợi ý. Ta có: |
b) Hệ quả
Từ định lí côsin suy ra
Củng cố hệ quả.
|
Ví dụ 2. Cho tam giác ABC có cạnh a=52,1; cạnh b=85; cạnh c=54. Tính số đo các góc |
Gợi ý. Các góc |
c) Áp dụng. Tính độ dài đường trung tuyến của tam giác.
Tiếp cận công thức tính độ dài đường trung tuyến.
Hoạt động 2.
|
Bài toán. Cho tam giác ABC có cạnh BC=a , cạnh AC=b và cạnh AB=c . Tính độ dài đường trung tuyến AM của tam giác ABC theo a,b,c. ( Với M là trung điểm của BC ) |
Gợi ý: Áp dụng định lí côsin trong tam giác AMB ta có: AM2=BA2+BM2-2BA.BM.cosB mà |
Công thức độ dài đường trung tuyến.
Gọi ma, mb, mc lần lượt là độ dài các đường trung tuyến của vẽ từ các đỉnh A,B,C của tam giác ABC .
Khi đó:
Củng cố.
|
Ví dụ 3. Cho tam giác ABC có cạnh a=7cm , cạnh b=8cm và cạnh c=6cm . Tính độ dài đường trung tuyến ma của tam giác |
Gợi ý: Áp dụng công thức đường trung tuyến |
d) Luyện tập
|
Câu 1. Tam giác ABC có các cạnh a,b,c thỏa mãn điều kiện (a+b+c)(a+b-c)=3ab. Tính số đo của góc C . |
Gợi ý: Ta có: |
|
Câu 2. Cho tam giác ABC có AB=5 , BC=7 và CA=8 . Tính |
Gợi ý: Ta có: |
|
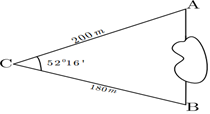
Câu 3. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định một điểm C mà từ đó có thể nhìn được A và B dưới một góc 52016' , biết CA=200m , BC=180m A. 163m B. 224m C. 112m D. 168m |
Gợi ý: Áp dụng định lí côsin trong tam giác ABC ta có: Vậy: Khoảng cách Khoảng cách từ A đến B xấp xỉ bằng 168m |
.....................................................................................................
.....................................................................................................
.....................................................................................................
.....................................................................................................
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Xem thêm các bài soạn Giáo án Toán lớp 10 theo hướng phát triển năng lực mới nhất, hay khác:
- Giáo án Toán 10 Bài 1: Giá trị lượng giác của một góc bất kì từ 0o đến 180o
- Giáo án Toán 10 Bài 2: Tích vô hướng của hai vectơ
- Giáo án Toán 10 Ôn tập chương 2 Hình học
- Giáo án Toán 10 Ôn tập chương 2 Hình học
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giáo án Toán 10 cả ba sách mới của chúng tôi được biên soạn bám sát chuẩn Giáo án môn Toán 10 của Bộ GD & ĐT.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 10 (các môn học)
- Giáo án điện tử lớp 10 (các môn học)
- Giáo án Ngữ văn 10
- Giáo án Toán 10
- Giáo án Tiếng Anh 10
- Giáo án Vật Lí 10
- Giáo án Hóa học 10
- Giáo án Sinh học 10
- Giáo án Lịch Sử 10
- Giáo án Địa Lí 10
- Giáo án Kinh tế Pháp luật 10
- Giáo án Tin học 10
- Giáo án Công nghệ 10
- Giáo án Giáo dục quốc phòng 10
- Giáo án Hoạt động trải nghiệm 10
- Đề thi lớp 10 (các môn học)
- Đề thi Ngữ Văn 10 (có đáp án)
- Chuyên đề Tiếng Việt lớp 10
- Đề cương ôn tập Văn 10
- Đề thi Toán 10 (có đáp án)
- Đề thi cương ôn tập Toán 10
- Đề thi Toán 10 cấu trúc mới (có đáp án)
- Đề thi Tiếng Anh 10 (có đáp án)
- Đề thi Vật Lí 10 (có đáp án)
- Đề thi Hóa học 10 (có đáp án)
- Đề thi Sinh học 10 (có đáp án)
- Đề thi Lịch Sử 10 (có đáp án)
- Đề thi Địa Lí 10 (có đáp án)
- Đề thi Kinh tế & Pháp luật 10 (có đáp án)
- Đề thi Tin học 10 (có đáp án)
- Đề thi Công nghệ 10 (có đáp án)
- Đề thi Giáo dục quốc phòng 10 (có đáp án)


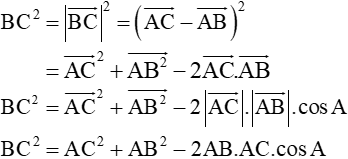
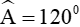 . Tính độ dài cạnh a
. Tính độ dài cạnh a 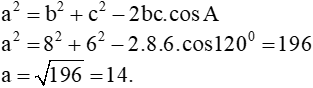
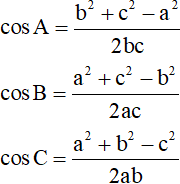
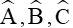 . Tính độ dài cạnh a
. Tính độ dài cạnh a 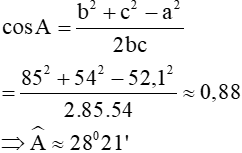
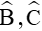 học sinh tính tương tự.
học sinh tính tương tự.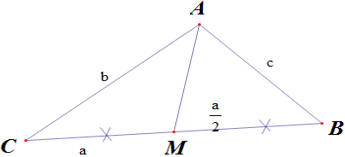
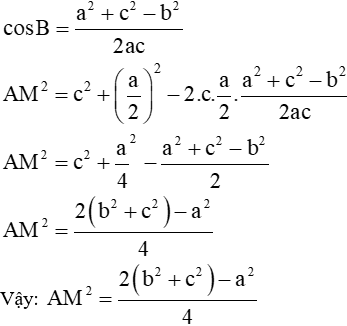
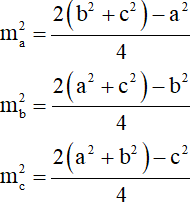
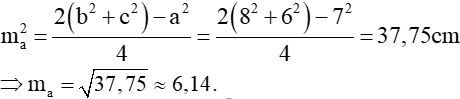
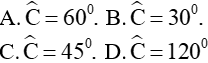
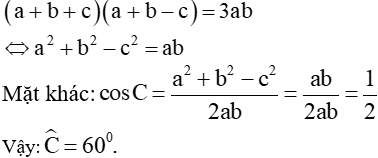
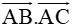
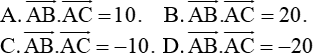
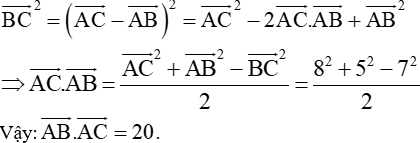




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

