Trọn bộ Công thức Vật Lí lớp 11 Chương 7: Mắt. Các dụng cụ quang quan trọng
Trọn bộ Công thức Vật Lí lớp 11 Chương 7: Mắt. Các dụng cụ quang quan trọng
Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Vật Lí lớp 11, VietJack biên soạn tài liệu trọn bộ công thức Vật Lí 11 Chương 7: Mắt. Các dụng cụ quang đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh vận dụng và làm bài tập thật tốt môn Vật Lí lớp 11.
Công thức tính góc lệch của tia sáng đơn sắc qua lăng kính hay, chi tiết
Công thức tính số bội giác của kính lúp khi ngắm chừng vô cực hay, chi tiết
Công thức tính khoảng cách từ vật đến thấu kính hay, chi tiết
Công thức Lăng kính đầy đủ, chi tiết
1. Định nghĩa
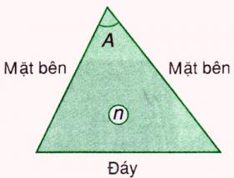
Lăng kính là một khối chất trong suốt, đồng chất, thường có dạng lăng trụ tam giác.

Một lăng kính được đặc trưng bởi:
+ Góc chiết quang A;
+ Chiết suất n.
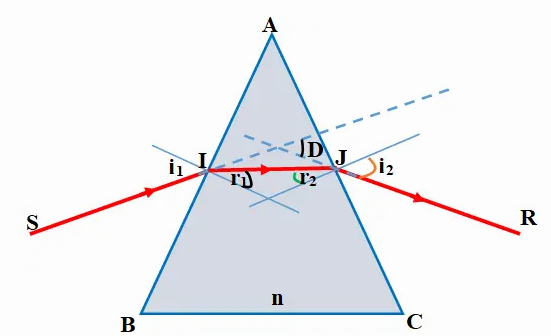
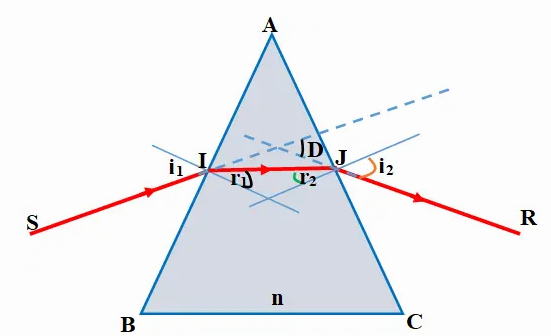
Chiếu đến mặt bên của lăng kính một chùm sáng hẹp đơn sắc SI.
+ Tại I: tia khúc xạ lệch gần pháp tuyến, nghĩa là lệch về phía đáy của lăng kính.
+ Tại J: tia khúc xạ lệch xa pháp tuyến, tức là cũng lệch về phía đáy của lăng kính.
Vậy, khi có tia ló ra khỏi lăng kính thì tia ló bao giờ cũng lệch về phía đáy của lăng kính so với tia tới.
Góc tạo bởi tia ló và tia tới gọi là góc lệch D của tia sáng khi truyền qua lăng kính.
2. Công thức – đơn vị đo
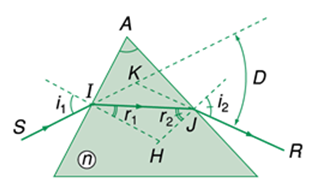
Xét một lăng kính có chiết suất n đặt trong không khí.
Công thức lăng kính:
- Tại I: sini1 = n.sin r1
- Tại J: sini2 = n.sin r2
- Góc chiết quang: A = r1 + r2
- Góc lệch của tia sáng qua lăng kính: D = i1 + i2 – A
Trong đó:
+ i1 là góc tới của tia sáng từ không khí vào lăng kính tại mặt bên thứ nhất (tại I);
+ i2 là góc ló của tia sáng đi từ lăng kính ra không khí từ mặt bên thứ hai (tại J);
+ D là góc lệch giữa tia tới và tia ló;
+ A là góc ở đỉnh
+ r1 là góc khúc xạ tại mặt bên thứ nhất (tại I)
+ r2 là góc tới của tia sáng tại mặt bên thứ hai (tại J)
3. Mở rộng
3.1 Nếu góc chiết quang A nhỏ (< 100), ta gọi lăng kính là nêm quang học.
Chiếu tới nêm quang học một tia tới có góc tới i nhỏ (i < 100), ta có các công thức lăng kính như sau:
i1 = nr1 ; i2 = nr2
A = r1 + r2
D = (n -1).A
3.2 Khi thay đổi góc tới i thì góc lệch D thay đổi qua một giá trị Dmin.
Khi đó
+ 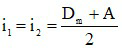
+ 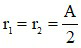
Chú ý: Nếu đo được A và Dm bằng thực nghiệm, có thể đo được chiết suất của lăng kính theo công thức:
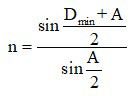
Khi đó đường truyền của tia sáng qua lăng kính như hình sau:
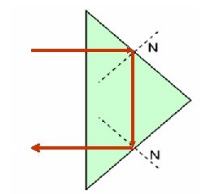
3.3 Lăng kính phản xạ toàn phần là lăng kính thủy tinh có tiết diện thẳng là một tam giác vuông cân. Lăng kính phản xạ toàn phần được sử dụng để tạo ảnh thuận chiều (ống nhòm, máy ảnh, …)

Đối với lăng kính đặt trong không khí, ta luôn có tia sáng đi từ không khí vào trong lăng kính, nhưng khi tia sáng đi từ lăng kính ra ngoài không khí, ta phải chú ý tính góc giới hạn phản xạ toàn phần bằng công thức:
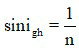
Nếu góc tới r2 > igh thì sẽ xảy ra hiện tượng phản xạ toàn phần.
3.4 Nếu lăng kính đặt trong môi trường có chiết suất n’, thì công thức lăng kính là:
n’sini1 = n.sin r1
n’sini2 = n.sin r2
A = r1 + r2
D = i1 + i2 - A
4. Bài tập ví dụ
Bài 1: Một lăng kính thủy tinh có chiết suất n = 1,41 ≈ √2. Tiết diện thẳng là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng cỉa tiết diện thẳng, tới AB với góc tới 450. Xác định đường truyền của tia sáng.
Bài giải:
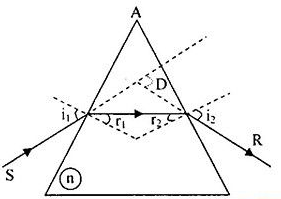
Tại I luôn có tia khúc xạ, ta có:
Sini1 = nsinr1
Sin r1 = 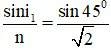 ⇒ r1 = 300
⇒ r1 = 300
Tại J: r2 = 600 – 300 = 300
Áp dụng công thức thấu kính, ta có: Sini2 = nsinr2 ⇒ i2 = 450
Bài 2: Một lăng kính thủy tinh P có chiết suất n = 1,5, tiết diện thẳng là một tam giác ABC vuông cân tại B.Chiếu vuông góc tới mặt AB một chùm sáng song song SI // BC.
a) Khối thủy tinh P ở trong không khí.Tính góc D làm bởi tia tới và tia ló
b) Tính lại góc D nếu khối P ở trong nước có chiết suất n’ = 1,33.
Bài giải:
a) Ta tính góc giới hạn phản xạ toàn phần của lăng kính này
sin igh = 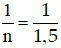 ⇒ igh = 41,810 = 420
⇒ igh = 41,810 = 420
Đường truyền của tia sáng qua lăng kính như sau
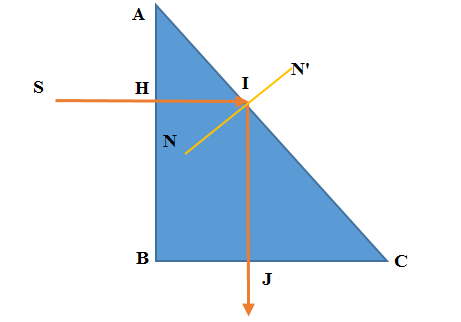
Tia sáng tới vuông góc với mặt bên nên truyền thẳng vào trong lăng kính.
Góc 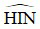 = 450 > igh ⇒ xảy ra phản xạ toàn phần tại I.
= 450 > igh ⇒ xảy ra phản xạ toàn phần tại I.
Góc phản xạ = góc tới ⇒ góc 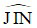 = góc
= góc 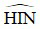 = 450
= 450
=> Góc 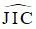 = 450
= 450
=> Góc 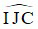 = 900
= 900
Góc lệch D = góc 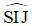 =900
=900
b)
Đặt lăng kính vào nước, ta có hình vẽ
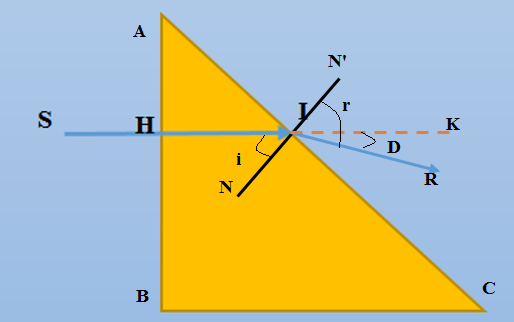
Sin igh = 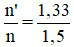 ⇒ igh = 630. Vì góc tới i = 450 < igh, nên sẽ xảy ra khúc xạ tại mặt AC.
⇒ igh = 630. Vì góc tới i = 450 < igh, nên sẽ xảy ra khúc xạ tại mặt AC.
Áp dụng công thức khúc xạ ánh sáng: n.sini = n’.sinr => 1,5.sin 450 = 1,33.sinr => r = 530
Góc lệch: D = |r – i| = |53 – 45| = 80
Công thức tính góc lệch của tia sáng đơn sắc qua lăng kính hay, chi tiết
1. Định nghĩa
Lăng kính là một khối chất trong suốt, đồng chất (thủy tinh, nhựa, …) thường có dạng lăng trụ tam giác.

Lăng kính có nhiều công dụng trong khoa học và kĩ thuật.

Máy quang phổ
Lăng kính là bộ phận chính của máy quang phổ. Máy này phân tích ánh sáng từ nguồn phát ra thành các thành phần đơn sắc, nhờ đó xác định được cấu tạo của nguồn sáng.
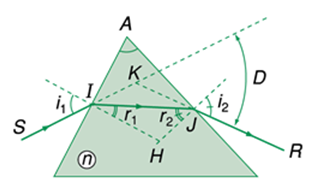
Chiếu đến mặt bên của lăng kính một chùm sáng hẹp đơn sắc SI.
+ Tại I: tia khúc xạ lệch gần pháp tuyến, nghĩa là lệch về phía đáy của lăng kính.
+ Tại J: tia khúc xạ lệch xa pháp tuyến, tức là cũng lệch về phía đáy của lăng kính.
Vậy, khi có tia ló ra khỏi lăng kính thì tia ló bao giờ cũng lệch về phía đáy của lăng kính so với tia tới.
Góc tạo bởi tia ló và tia tới gọi là góc lệch D của tia sáng khi truyền qua lăng kính.
2. Công thức – đơn vị đo
Góc lệch D được xác định bằng công thức:
D = i1 + i2 - A
Trong đó:
+ i1 là góc tới của tia sáng từ không khí vào lăng kính tại mặt bên thứ nhất (tại I);
+ i2 là góc ló của tia sáng đi từ lăng kính ra không khí từ mặt bên thứ hai (tại J);
+ D là góc lệch giữa tia tới và tia ló;
+ A là góc ở đỉnh
Góc i2 được xác định từ các công thức lăng kính:
sini1 = n.sin r1
sini2 = n.sin r2
A = r1 + r2
Trong đó:
+ A là góc ở đỉnh
+ r1 là góc khúc xạ tại mặt bên thứ nhất (tại I)
+ r2 là góc tới của tia sáng tại mặt bên thứ hai (tại J)
3. Mở rộng
3.1 Nếu góc chiết quang A nhỏ (< 100), ta gọi lăng kính là nêm quang học.
Chiếu tới nêm quang học một tia tới có góc tới i nhỏ (i < 100), ta có các công thức góc lệch giữa tia tới và tia ló của lăng kính như sau:
D = (n - 1).A
3.2 Khi thay đổi góc tới i thì góc lệch D thay đổi qua một giá trị Dmin.
Khi đó
+ 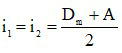
+ 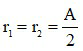
+ 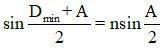
Khi đó đường truyền của tia sáng qua lăng kính như hình sau:
4. Bài tập ví dụ
Bài 1: Cho một tia sáng đơn sắc đi qua lăng kính có góc chiết quang A = 600 và thu được góc lệch cực tiểu Dm = 600. Chiết suất của lăng kính là bao nhiêu?
Bài giải:
Áp dụng công thức tính góc lệch cực tiểu
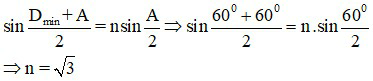
Đáp án: n = √3
Bài 2: Một lăng kính có góc chiết quang A = 80, chiết suất n = 1,5. Chiếu tới mặt bên của lăng kính một tia đơn sắc với góc tới i rất nhỏ. Tính góc lệch của tia ló với tia tới.
Bài giải:
Áp dụng công thức tính góc lệch với nêm quang học:
D = (n - 1).A = (1,5 - 1).80 = 40
Đáp án: D = 40
Công thức Thấu kính đầy đủ, chi tiết
1. Định nghĩa
Thấu kính là một khối chất trong suốt giới hạn bởi hai mặt cong hoặc bởi một mặt cong và một mặt phẳng.
- Phân loại theo hình dạng:
+ Thấu kính lồi (rìa mỏng).

+ Thấu kính lõm (rìa dày).

- Phân loại theo đường truyền của chùm tia sáng song song qua thấu kính khi đặt thấu kính trong không khí:
+ Thấu kính lồi là thấu kính hội tụ.
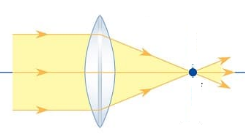
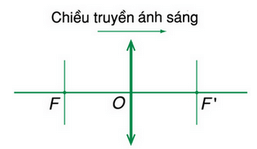
Thấu kính hội tụ được quy ước vẽ như sau:
+ Thấu kính lõm là thấu kính phân kỳ.
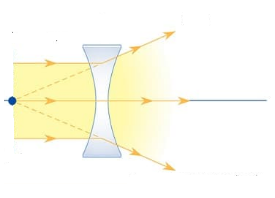
Thấu kính phân kì được quy ước vẽ như sau:

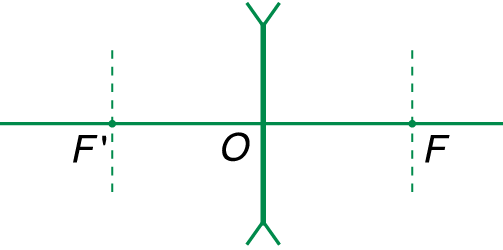
+ Quang tâm O là điểm chính giữa của thấu kính mỏng mà mọi tia sáng tới truyền qua O đều truyền thẳng qua thấu kính.
+ Đường thẳng đi qua quang tâm O và vuông góc với mặt thấu kính là trục chính của thấu kính.
+ Các đường thẳng qua quang tâm O là trục phụ của thấu kính.
+ Chùm tia sáng song song với trục chính sau khi qua thấu kính sẽ hội tụ tại tiêu điểm chính của thấu kính (đối với thấu kính hội tụ) hoặc có đường kéo dài hội tụ tại tiêu điểm chính của thấu kính (đối với thấu kính phân kì).
Mỗi thấu kính có hai tiêu điểm chính F (tiêu điểm vật) và F’ (tiêu điểm ảnh) đối xứng với nhau qua quang tâm.
+ Chùm tia sáng song song với một trục phụ sau khi qua thấu kính sẽ hội tụ tại tiêu điểm phụ của thấu kính (đối với thấu kính hội tụ) hoặc có đường kéo dài hội tụ tại tiêu điểm phụ của thấu kính (đối với thấu kính phân kì).
Mỗi thấu kính có vô số các tiêu điểm vật phụ Fn và các tiêu điểm ảnh phụ Fn’.
+ Tập hợp tất cả các tiêu điểm tạo thành tiêu diện. Mỗi thấu kính có hai tiêu diện: tiêu diện vật và tiêu diện ảnh.
Có thể coi tiêu diện là mặt phẳng vuông góc với trục chính qua tiêu điểm chính.
Khái niệm ảnh và vật trong quang học:
+ Ảnh điểm là điểm đồng qui của chùm tia ló hay đường kéo dài của chúng,
+ Ảnh điểm là thật nếu chùm tia ló là chùm hội tụ, ảo nếu chùm tia ló là chùm phân kì.
+ Vật điểm là điểm đồng qui của chùm tia tới hoặc đường kéo dài của chúng.
+ Vật điểm là thật nếu chùm tia tới là chùm phân kì, ảo nếu chùm tia tới là chùm hội tụ.
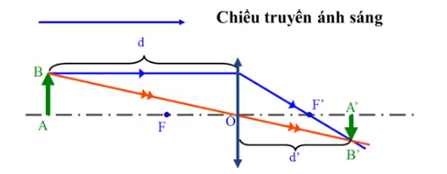
Khi đặt vật sáng trước thấu kính thì thu được ảnh của vật, có thể là ảnh thật hoặc ảnh ảo.
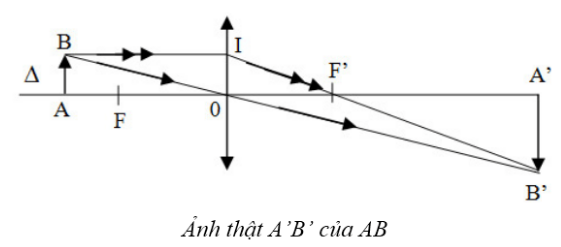
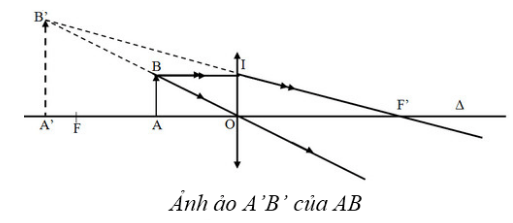
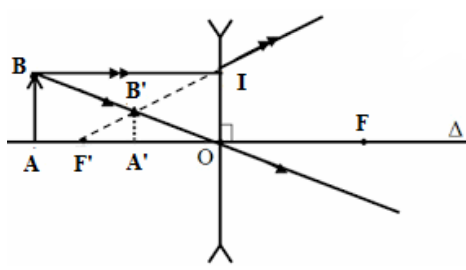
Ảnh ảo A’B’ của AB
2. Công thức – đơn vị đo
Công thức xác định vị trí ảnh: 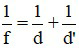
Công thức xác định số phóng đại: 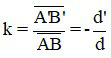
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị cm hoặc m. Đối với thấu kính hội tụ f >0; đối với thấu kính phân kì f < 0.
+ d là khoảng cách từ vật đến thấu kính, có đơn vị cm hoặc m. Nếu vật thật d > 0; nếu vật ảo d < 0.
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị cm hoặc m. Nếu ảnh thật d’ > 0; nếu ảnh ảo d’ < 0.
+ k là số phóng đại ảnh. Nếu k > 0: ảnh và vật cùng chiều; nếu k < 0: ảnh và vật ngược chiều. Nếu |k| > 1: ảnh lớn hơn vật; nếu |k| < 1: ảnh nhỏ hơn vật.
+ 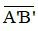 là độ cao của ảnh, có đơn vị cm hoặc m.
là độ cao của ảnh, có đơn vị cm hoặc m.
+ 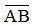 là độ cao của vật, có đơn vị cm hoặc m.
là độ cao của vật, có đơn vị cm hoặc m.
3. Mở rộng
Từ công thức xác định vị trí ảnh, ta có thể xác định tiêu cự f, vị trí vật, vị trí ảnh như sau:
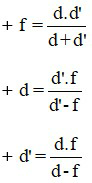
Kết hợp công thức xác định vị trí ảnh và công thức số phóng đại, ta có:
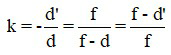
Khi biết số phóng đại ảnh, ta có d’ = - k.d.
Khi chỉ biết ảnh lớn hay nhỏ hơn bao nhiêu lần vật thì ta có |d| = |k|.|d’|
4. Bài tập ví dụ
Bài 1: Cho một thấu kính hội tụ có tiêu cự f = 20 cm. Đặt một vật sáng AB cao 2 cm trước thấu kính và cách thấu kính 60 cm. Xác định vị trí và chiều cao của ảnh.
Bài giải:
Áp dụng công thức thấu kính:
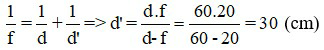
Áp dụng công thức độ phóng đại ảnh
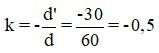
Mà 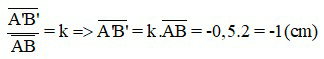
Vậy ảnh A’B’ cao 1 cm, dấu “-” cho biết ảnh ngược chiều với vật.
Bài 2: Cho một thấu kính phân kì có tiêu cự f = - 20 cm. Đặt một vật sáng AB cao 2 cm trước thấu kính và cách thấu kính 20 cm. Xác định vị trí và chiều cao của ảnh.
Bài giải:
Áp dụng công thức thấu kính:
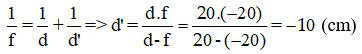
Áp dụng công thức độ phóng đại ảnh
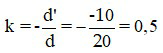
Mà 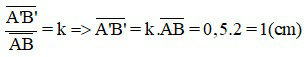
Vậy ảnh A’B’ cao 1 cm, ảnh cùng chiều với vật.
Công thức tính tiêu cự hay, chi tiết
1. Định nghĩa
Tiêu cự là độ dài đại số, kí hiệu là f, có trị số tuyệt đối bằng khoảng cách từ quang tâm O đến tiêu điểm chính của thấu kính, có đơn vị là cm hoặc m.
|f| = OF = OF’
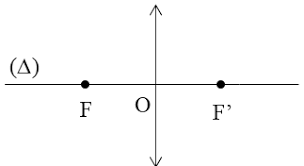
Thấu kính hội tụ
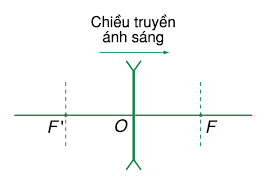
Thấu kính phân kỳ
Quy ước: f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì.
2. Công thức – đơn vị đo
Khi đặt vật sáng trước thấu kính, ta thu được ảnh của vật. Khi biết vị trí ảnh và vật, ta có thể xác định tiêu cự của thấu kính bởi công thức:
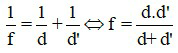
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị cm hoặc m. Đối với thấu kính hội tụ f >0; đối với thấu kính phân kì f < 0.
+ d là khoảng cách từ vật đến thấu kính, có đơn vị cm hoặc m. Nếu vật thật d > 0; nếu vật ảo d < 0.
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị cm hoặc m. Nếu ảnh thật d’ > 0; nếu ảnh ảo d’ < 0.
Khi biết độ tụ của thấu kính, ta có thể tính tiêu cự bằng công thức
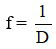
Trong đó:
+ D là độ tụ, có đơn vị đi ốp (kí hiệu là dp); D > 0 với thấu kính hội tụ; D < 0 với thấu kính phân kì.
+ f là tiêu cự, có đơn vị là mét (m).
Thấu kính hội tụ có khả năng hội tụ chùm sáng càng mạnh khi f càng nhỏ.
3. Mở rộng
3.1 Riêng với thấu kính mỏng, khi biết các bán kính cong của thấu kính, ta có thể tính tiêu cự bởi công thức:
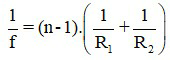
Trong đó:
+ f là tiêu cự, f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì. Đơn vị đo của f là mét hoặc dm, cm.
+ n là chiết suất tỉ đối của vật liệu làm thấu kính với môi trường xung quanh thấu kính.
+ R1 và R2 là các bán kính của các mặt thấu kính, với quy ước
R1, R2 > 0 đối với các mặt lồi,
R1, R2 < 0 đối với các mặt lõm,
R1, R2 = 0 đối với các mặt phẳng.
3.2 Với hệ hai thấu kính mỏng đồng trục ghép sát, ta có thể xác định tiêu cự của thấu kính tương đương bởi công thức:
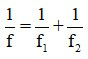
Trong đó:
+ f là tiêu cự thấu kính tương đương, có đơn vị m;
+ f1 và f2 lần lượt là tiêu cực của các thấu kính trong hệ ghép sát đồng trục, có đơn vị m.
3.3 Với mắt người bình thường, vật sáng ở trước mắt luôn cho ảnh hiện trên võng mạc, nên tiêu cự của thể thủy tinh được xác định bằng công thức
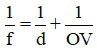
4. Bài tập ví dụ
Bài 1: Một kính lão có ghi độ tụ là - 2 dp. Tính tiêu cự của kính?
Bài giải:
Áp dụng công thức f = 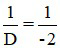 = -0,5 (m)
= -0,5 (m)
Đây là thấu kính phân kì có tiêu cự f = - 0,5 m
Đáp án: f = - 0,5 m
Bài 2: Một vật sáng AB đặt trước thấu kính và cách thấu kính 20 cm, cho ảnh ảo cách thấu kính 10 cm. Tính tiêu cự của kính. Đây là thấu kính loại gì?
Bài giải:
Vì vật thật nên d = 20 cm; ảnh ảo nên d’ = - 10 cm
Áp dụng công thức 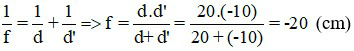
Đây là thấu kính phân kì.
Đáp án: f = - 20 cm
Bài 3: Một người mắt tốt có võng mạc cách mắt 2,5 cm có thể nhìn xa vô cùng mà không phải điều tiết. Khi đó tiêu cự của thể thủy tinh là bao nhiêu?
Bài giải:
Vì vật ở xa vô cùng nên d = ∞, ảnh thật hiện lên võng mạc nên d’ = 2,5 cm.
Ta có 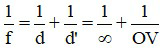 ⇒ f = OV = 2,5 cm.
⇒ f = OV = 2,5 cm.
Đây là trường hợp tiêu cự của mắt dài nhất.
Đáp án: khi nhìn vật ở xa vô cùng fm = 2,5 cm.
Công thức tính tiêu cự của thấu kính mỏng hay, chi tiết
1. Định nghĩa
Thấu kính là một khối chất trong suốt giới hạn bởi hai mặt cong hoặc bởi một mặt cong và một mặt phẵng.
Phân loại theo hình dạng:
+ Thấu kính lồi (rìa mỏng).

+ Thấu kính lõm (rìa dày).

Phân loại theo đường truyền của chùm tia sáng song song qua thấu kính khi đặt thấu kính trong không khí:
+ Thấu kính lồi là thấu kính hội tụ.
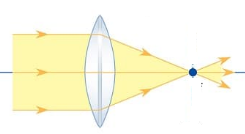
+ Thấu kính lõm là thấu kính phân kỳ.
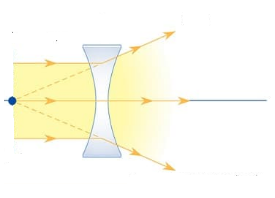
+ Quang tâm O là điểm chính giữa của thấu kính mỏng mà mọi tia sáng tới truyền qua O đều truyền thẳng qua thấu kính.
+ Đường thẳng đi qua quang tâm O và vuông góc với mặt thấu kính là trục chính của thấu kính.
+ Các đường thẳng qua quang tâm O là trục phụ của thấu kính.
+ Chùm tia sáng song song với trục chính sau khi qua thấu kính sẽ hội tụ tại tiêu điểm chính của thấu kính (đối với thấu kính hội tụ) hoặc có đường kéo dài hội tụ tại tiêu điểm chính của thấu kính (đối với thấu kính phân kì).
Mỗi thấu kính có hai tiêu điểm chính F (tiêu điểm vật) và F’ (tiêu điểm ảnh) đối xứng với nhau qua quang tâm.
+ Chùm tia sáng song song với một trục phụ sau khi qua thấu kính sẽ hội tụ tại tiêu điểm phụ của thấu kính (đối với thấu kính hội tụ) hoặc có đường kéo dài hội tụ tại tiêu điểm phụ của thấu kính (đối với thấu kính phân kì).
Mỗi thấu kính có vô số các tiêu điểm vật phụ Fn và các tiêu điểm ảnh phụ Fn’.
+ Tập hợp tất cả các tiêu điểm tạo thành tiêu diện. Mỗi thấu kính có hai tiêu diện: tiêu diện vật và tiêu diện ảnh.
Có thể coi tiêu diện là mặt phẳng vuông góc với trục chính qua tiêu điểm chính.
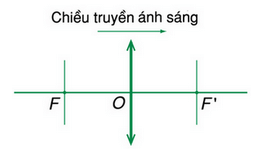
Tiêu cự là độ dài đại số, kí hiệu là f, có trị số tuyệt đối bằng khoảng cách từ quang tâm O đến tiêu điểm chính của thấu kính, có đơn vị là cm hoặc m.
|f| = OF = OF’
Quy ước: f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì.
Đơn vị đo của f là mét hoặc dm, cm.
2. Công thức – đơn vị đo
Công thức xác định tiêu cự của thấu kính:
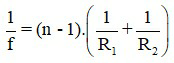
Trong đó:
+ f là tiêu cự, f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì. Đơn vị đo của f là mét hoặc dm, cm.
+ n là chiết suất tỉ đối của vật liệu làm thấu kính với môi trường xung quanh thấu kính.
+ R1 và R2 là các bán kính của các mặt thấu kính, với quy ước
R1, R2 > 0 đối với các mặt lồi,
R1, R2 < 0 đối với các mặt lõm,
R1, R2 = 0 đối với các mặt phẳng.
3. Mở rộng
3.1 Thấu kính có khả năng hội tụ càng mạnh khi độ lớn của tiêu cự càng nhỏ. Do đó, người ta định nghĩa độ tụ của thấu kính là D = 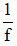
Trong đó:
+ D là độ tụ, có đơn vị đi ốp (kí hiệu là dp); D > 0 với thấu kính hội tụ; D < 0 với thấu kính phân kì.
+ f là tiêu cự, có đơn vị là mét (m).
Do đó, khi biết độ tụ của một thấu kính, ta có thể xác định tiêu cự bằng công thức:
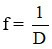
3.2 Khi đặt vật sáng trước thấu kính, ta thu được ảnh của vật. Khi biết vị trí ảnh và vật, ta có thể xác định tiêu cự của thấu kính bởi công thức:
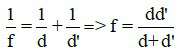
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị cm hoặc m. Đối với thấu kính hội tụ f >0; đối với thấu kính phân kì f < 0.
+ d là khoảng cách từ vật đến thấu kính, có đơn vị cm hoặc m. Nếu vật thật d > 0; nếu vật ảo d < 0.
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị cm hoặc m. Nếu ảnh thật d’ > 0; nếu ảnh ảo d’ < 0.
3.3 Với hệ hai thấu kính mỏng đồng trục ghép sát, ta có thể xác định tiêu cự của thấu kính tương đương bởi công thức:
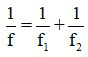
Trong đó:
+ f là tiêu cự thấu kính tương đương, có đơn vị m;
+ f1 và f2 lần lượt là tiêu cực của các thấu kính trong hệ ghép sát đồng trục, có đơn vị m.
4. Bài tập ví dụ
Bài 1: Một thấu kính phẳng lồi, có bán kính mặt lồi là 25 cm, được làm bằng thủy tinh có chiết suất 1,5. Tính tiêu cự của thấu kính này.
Bài giải:
Áp dụng công thức:
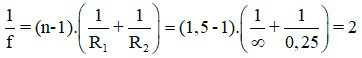
Đáp án: f = 0,5 m
Bài 2: Một vật sáng AB đặt trước thấu kính và cách thấu kính 20 cm, cho ảnh ảo cách thấu kính 10 cm. Tính tiêu cự của kính. Đây là thấu kính loại gì?
Bài giải:
Vì vật thật nên d = 20 cm; ảnh ảo nên d’ = - 10 cm
Áp dụng công thức 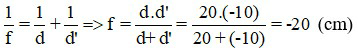
Đây là thấu kính phân kì.
Đáp án: f = - 20 cm
Bài 3: Cho hai thấu kính hội tụ ghép sát đồng trục có tiêu cự lần lượt là 20 cm và 25 cm. Tính tiêu cự của hệ này.
Bài giải:
Áp dụng công thức
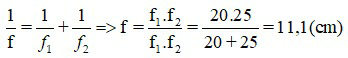
Đáp án: f = 11,1 cm.
Công thức tính tiêu cự của kính lúp hay, chi tiết
1. Định nghĩa
Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ. Kính lúp có tác dụng tạo ảnh với góc trông lớn hơn góc trông vật nhiều lần.
Kính lúp được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cỡ cm).

Cách sử dụng kính lúp
+ Đặt vật trong khoảng từ quang tâm O đến tiêu điểm vật chính F của kính lúp để có ảnh ảo cùng chiều và lớn hơn vật.
+ Ngắm chừng: điều chỉnh khoảng cách từ vật đến thấu kính để ảnh hiện ra trong giới hạn nhìn rõ của mắt.
+ Khi cần quan sát trong một thời gian dài, ta nên thực hiện cách ngắm chừng ở cực viễn để mắt không bị mỏi.
Số bội giáclà đại lượng đặc trưng cho các dụng cụ quang học bổ trợ cho mắt, được xác định bằng thương số giữa góc trông ảnh qua dụng cụ quang học và góc trông trực tiếp vật:
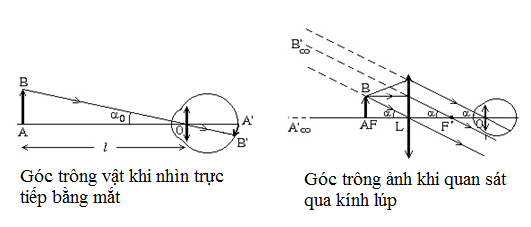
Số bội giác: G =
Đối với kính lúp, số bội giác khi ngắm chừng ở vô cực là G = 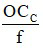
Trong đó:
+ f là tiêu cự của kính lúp, có đơn vị cm hoặc m.
+ OCC là khoảng cực cận của mắt, thường lấy là 25 cm = 0,25 m
+ G là số bội giác khi ngắm chừng ở vô cực.
Trên thân kính lúp thường có ghi sẵn số bội giác (2x; 5x; 10x…)
Ví dụ: số 10X ở đây cho biết G = 10

2. Công thức – đơn vị đo
Khi biết số bội giác của kính lúp, ta xác định tiêu cự của kính lúp bằng công thức:
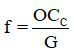
Trong đó:
+ f là tiêu cự của kính lúp, có đơn vị cm hoặc m.
+ OCC là khoảng cực cận của mắt, thường lấy là 25 cm = 0,25 m
+ G là số bội giác khi ngắm chừng ở vô cực.
Chú ý: trong công thức này, f và OCc phải có cùng đơn vị đo.
Khi biết vị trí vật đặt trước kính lúp và vị trí ảnh tạo bởi kính lúp, ta xác định tiêu cự của kính lúp bằng công thức:
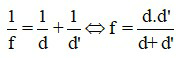
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị cm hoặc m. Đối với kính lúp f > 0.
+ d là khoảng cách từ vật đến thấu kính, có đơn vị cm hoặc m. Nếu vật thật d > 0; nếu vật ảo d < 0.
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị cm hoặc m. Nếu ảnh thật d’ > 0; nếu ảnh ảo d’ < 0.
Chú ý: khi áp dụng công thức này f, d, d’ phải có cùng đơn vị đo.
3. Mở rộng
Khi biết độ tụ của kính lúp, ta có thể xác định tiêu cự của kính lúp bằng công thức:
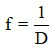
Trong đó:
+ f là tiêu cự của kính, có đơn vị mét (m);
+ D là độ tụ của kính, có đơn vị diôp (dp).
4. Bài tập ví dụ
Bài 1: Một kính lúp có ghi số 5X trên thân, tiêu cự của kính lúp này là bao nhiêu?
Bài giải:
Số 5X trên thân cho biết kính lúp này có số bội giác khi ngắm chừng ở vô cực G = 5.
Vậy tiêu cự của kính này là: 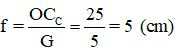
Bài 2: Một học sinh có điểm cực cận cách mắt 15 cm dùng kính lúp để quan sát các vật nhỏ. Khi đặt vật trước kính 2,5 cm thì ảnh hiện ra tại cực cận của mắt. Mắt đặt cách kính 10 cm. Hãy tính tiêu cự của kính lúp này.
Bài giải:
Ảnh ảo hiện ra ở cực cận cách mắt 15 cm, mà kính đặt cách mắt 10 cm, nên ảnh này cách kính 5 cm, ta có d’ = - 5cm.
Vật đặt trước kính 2,5 cm nên d = 2,5 cm.
Áp dụng công thức thấu kính, ta có:
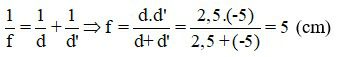
Đáp án: f = 5 cm.
Công thức tính tiêu cự của mắt hay, chi tiết
1. Định nghĩa
- Mắt là một hệ gồm nhiều môi trường trong suốt tiếp giáp nhau bằng các mặt cầu.
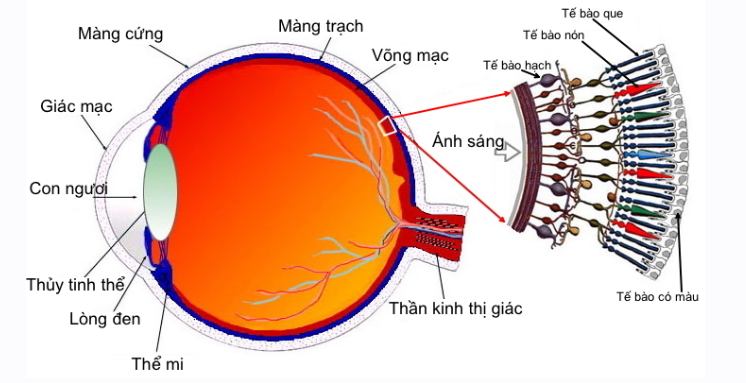
- Từ ngoài vào trong, mắt có các bộ phận sau:
+ Giác mạc: Màng cứng, trong suốt. Bảo vệ các phần tử bên trong và làm khúc xạ các tia sáng truyền vào mắt.
+ Thủy dịch: Chất lỏng trong suốt có chiết suất xấp xỉ bằng chiết suất của nước.
+ Lòng đen: Màn chắn, ở giữa có lỗ trống gọi là con ngươi. Con ngươi có đường kính thay đổi tự động tùy theo cường độ sáng.
+ Thể thủy tinh: Khối chất đặc trong suốt có hình dạng thấu kính hai mặt lồi.
+ Dịch thủy tinh: Chất lỏng giống chất keo loãng, lấp đầy nhãn cầu sau thể thủy tinh.
+ Màng lưới (võng mạc): tại đó tập trung đầu các sợi dây thần kinh thị giác. Ở màng lưới có điểm vàng V là nơi cảm nhận ánh sáng nhạy nhất và điểm mù không nhạy cảm với ánh sáng.
- Hệ quang học của mắt được coi tương đương một thấu kính hội tụ gọi là thấu kính mắt.
Khi nhìn các vật ở các khoảng cách khác nhau (d thay đổi) thì mắt sẽ điều tiết để thay đổi f của thấu kính mắt sao cho ảnh hiện đúng trên màng lưới.
+ Khi mắt ở trạng thái không điều tiết, tiêu cự của mắt lớn nhất (fmax, Dmin).
+ Khi mắt điều tiết tối đa, tiêu cự của mắt nhỏ nhất (fmin, Dmax).
2. Công thức – đơn vị đo
Với mắt người bình thường, vật sáng ở trước mắt luôn cho ảnh hiện trên võng mạc, nên tiêu cự của thể thủy tinh được xác định bằng công thức:
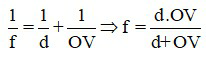
3. Mở rộng
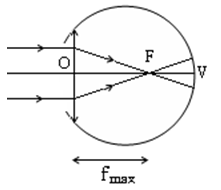
- Với mắt có tật cận thị
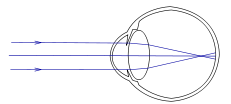
+ Chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm trước màng lưới.
+ fmax < OV.
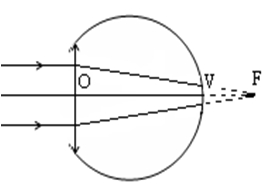
- Với mặt có tật viễn thị
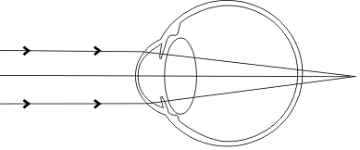
+ chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm sau màng lưới.
+ fmax > OV.
4. Bài tập ví dụ
Bài 1. Một người có mắt bình thường (không có tật) nhìn thấy được các vật ở rất xa mà không phải điều tiết. Khoảng cực cận của người này là OCc = 25 cm. Tính tiêu cự của mắt người này khi điều tiết tối đa và khi không điều tiết. Biết khoảng cách từ thể thủy tinh đến võng mạc là 2,5 cm.
Bài giải
Khi mắt nhìn vật ở xa vô cùng thì mắt không cần điều tiết, nên ta có
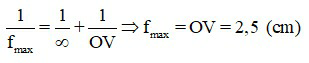
Khi mắt nhìn vật ở điểm cực cận, cách măt 25 cm, mắt cần điều tiết tối đa, ta có
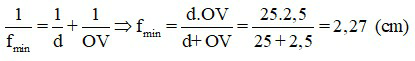
Đáp án: fmax = 2,5 cm; fmin = 2,27 cm
Bài 2. Một người bị cận thị, có điểm cực cận cách mắt 10 cm. Tính tiêu cự của mắt người này khi điều tiết tối đa, biết OV = 2,5 cm.
Bài giải
Khi mắt nhìn vật ở điểm cực cận, cách mắt 25 cm, mắt cần điều tiết tối đa, ta có
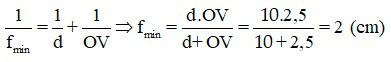
Đáp án: f = 2 cm
Công thức tính độ tụ hay, chi tiết
1. Định nghĩa
Độ tụ là đại lượng vật lý đặc trưng cho khả năng hội tụ ánh sáng của thấu kính.
2. Công thức – đơn vị đo
Công thức độ tụ: D = 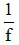
Trong đó:
+ D là độ tụ
+ f là tiêu cự của thấu kính, có đơn vị là mét (m).
Đơn vị của độ tụ là điôp, kí hiệu là dp : 1 dp = 1 m-1.
Qui ước:
+ thấu kính hội tụ: f > 0 ; D > 0
+ thấu kính phân kì: f < 0; D < 0
3. Mở rộng
3.1 Riêng với thấu kính mỏng, khi biết các bán kính cong của thấu kính, ta có thể tính độ tụ bởi công thức:
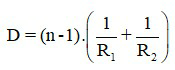
Trong đó:
+ D là độ tụ, D > 0 với thấu kính hội tụ; D< 0 với thấu kính phân kì. Đơn vị đo của D là diop (dp).
+ n là chiết suất tỉ đối của vật liệu làm thấu kính với môi trường xung quanh thấu kính.
+ R1 và R2 là các bán kính của các mặt thấu kính, có đơn vị mét (m), với quy ước:
R1, R2 > 0 đối với các mặt lồi,
R1, R2 < 0 đối với các mặt lõm,
R1, R2 = 0 đối với các mặt phẳng.
3.2 Với hệ hai thấu kính mỏng đồng trục ghép sát, ta có thể xác định độ tụ của thấu kính tương đương bởi công thức:
D = D1 + D2
Trong đó:
+ D là độ tụ thấu kính tương đương, có đơn vị dp;
+ D1 và D2 lần lượt là độ tụ của các thấu kính trong hệ ghép sát đồng trục, có đơn vị dp.
3.3 Với mắt người bình thường, vật sáng ở trước mắt luôn cho ảnh hiện trên võng mạc, nên độ tụ của thể thủy tinh được xác định bằng công thức
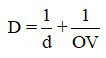
Trong đó:
+ D là độ tụ của mắt, có đơn vị dp;
+ d là khoảng cách từ vật đến mắt, có đơn vị mét (m);
+ OV là khoảng cách từ mắt đến võng mạc, có đơn vị mét (m).
3.4 Trong trường hợp biết vị trí vật và ảnh tạo bởi thấu kính, ta có thể dùng công thức thấu kính để xác định độ tụ của thấu kính:
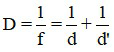
Trong đó:
+ D là độ tụ của thấu kính, có đơn vị dp;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét (m);
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét (m).
4. Bài tập ví dụ
Bài 1.
Một thấu kính có tiêu cự f = 20 cm. Tính độ tụ của thấu kính này, cho biết đây là loại thấu kính gì?
Bài giải:
Đổi f = 20 cm = 0,2 m.
Độ tụ của thấu kính này là D = 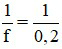 = 5 (dp)
= 5 (dp)
Đây là thấu kính hội tụ (D>0).
Đáp án: D = 5 dp
Bài 2: Mắt một người bình thường có thể nhìn một vật ở xa vô cùng mà không phải điều tiết, ảnh hiện trên võng mạc cách thể thủy tinh 2,5 cm. Tính độ tụ của mắt khi đó.
Bài giải:
Áp dụng công thức D = 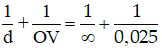 = 40 (dp)
= 40 (dp)
Đáp án: D = 40 dp
Bài 3: Hệ 2 thấu kính ghép sát, gồm có thấu kính hội tụ có tiêu cự f1 = 20 cm và thấu kính phân kì có tiêu cự f2 = - 10 cm. Tính độ tụ của thấu kính tương đương.
Bài giải:
Đổi f1 = 20 cm = 0,2 m; f2 = - 10 cm = - 0,1 m
Áp dụng công thức về độ tụ của hệ thấu kính ghép sát:
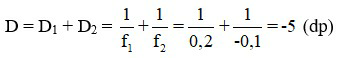
Đáp án: D = - 5dp.
Công thức tính độ tụ của thấu kính hay, chi tiết
1. Định nghĩa
Độ tụ là đại lượng vật lý đặc trưng cho khả năng hội tụ ánh sáng của thấu kính.
2. Công thức – đơn vị đo
Công thức độ tụ: D = 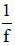
Trong đó:
+ D là độ tụ
+ f là tiêu cự của thấu kính, có đơn vị là mét (m).
Đơn vị của độ tụ là điôp, kí hiệu là dp : 1 dp = 1 m-1.
Qui ước:
+ thấu kính hội tụ: f > 0 ; D > 0
+ thấu kính phân kì: f < 0; D < 0
Với thấu kính mỏng, khi biết các bán kính cong của thấu kính, ta có thể tính độ tụ bởi công thức:
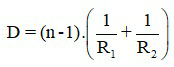
Trong đó:
+ D là độ tụ, D > 0 với thấu kính hội tụ; D < 0 với thấu kính phân kì. Đơn vị đo của D là diop (dp).
+ n là chiết suất tỉ đối của vật liệu làm thấu kính với môi trường xung quanh thấu kính.
+ R1 và R2 là các bán kính của các mặt thấu kính, có đơn vị mét (m), với quy ước:
R1, R2 > 0 đối với các mặt lồi,
R1, R2 < 0 đối với các mặt lõm,
R1, R2 = 0 đối với các mặt phẳng.
3. Mở rộng
Khi biết độ tụ của thấu kính, ta có thể xác định tiêu cự của thấu kính f = 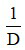
Khi biết vị trí vật và ảnh của vật tạo bởi thấu kính, ta có thể xác định độ tụ của thấu kính bởi công thức thấu kính:
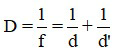
Trong đó:
+ D là độ tụ của thấu kính, có đơn vị dp;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét (m);
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét (m).
Với hệ hai thấu kính mỏng đồng trục ghép sát, ta có thể xác định độ tụ của thấu kính tương đương bởi công thức:
D = D1 + D2
Trong đó:
+ D là độ tụ thấu kính tương đương, có đơn vị dp;
+ D1 và D2 lần lượt là độ tụ của các thấu kính trong hệ ghép sát đồng trục, có đơn vị dp.
4. Bài tập ví dụ
Bài 1:
Một thấu kính có tiêu cự f = - 20 cm. Tính độ tụ của thấu kính này, cho biết đây là loại thấu kính gì?
Bài giải:
Đổi f = - 20 cm = - 0,2 m.
Độ tụ của thấu kính này là D = 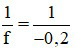 = -5 (dp)
= -5 (dp)
Đây là thấu kính phân kì (D < 0).
Đáp án: D = -5 dp
Bài 2: Đặt một vật sáng AB trước thấu kính hội tụ và cách thấu kính 30 cm, thu được một ảnh thật cách thấu kính 60 cm. Hãy xác định độ tụ của thấu kính này.
Bài giải:
Áp dụng công thức thấu kính, ta có:
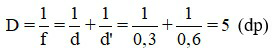
Đáp án: 5 dp
Bài 3: Một thấu kính phẳng lồi, có bán kính mặt lồi là 25 cm, được làm bằng thủy tinh có chiết suất 1,5. Tính tiêu cự của thấu kính này.
Bài giải:
Đổi 25 cm = 0,25 m
Áp dụng công thức:
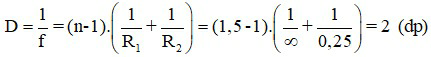
Đáp án: D = 2 dp
Công thức tính độ tụ của mắt hay, chi tiết
1. Định nghĩa
- Mắt là một hệ gồm nhiều môi trường trong suốt tiếp giáp nhau bằng các mặt cầu.
- Điểm xa nhất trên trục chính của mắt mà vật đặt tại đó thì ảnh của vật nằm trên võng mạc gọi là điểm cực viễn (CV).
- Điểm gần nhất trên trục chính của mắt mà vật đặt tại đó thì ảnh của vật nằm trên võng mạc gọi là điểm cực cận (CC).
- Khoảng cách từ điểm cực cận (CC) đến điểm cực viễn (CV) gọi là khoảng thấy rõ của mắt.
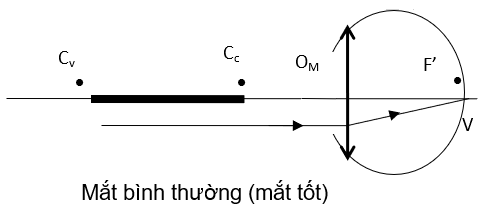
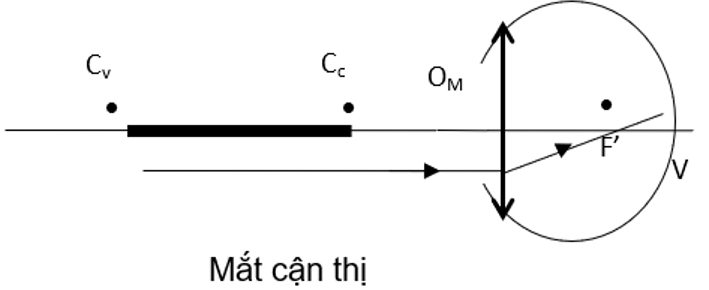
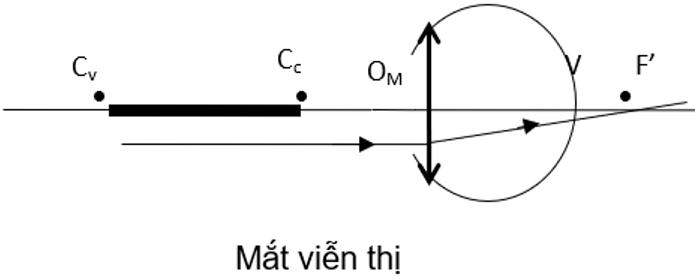
- Hệ quang học của mắt được coi tương đương một thấu kính hội tụ gọi là thấu kính mắt. Độ tụ của mắt là đại lượng vật lý đặc trưng cho khả năng hội tụ ánh sáng của mắt.
- Khi nhìn các vật ở các khoảng cách khác nhau (d thay đổi) thì mắt sẽ điều tiết để thay đổi f của thấu kính mắt sao cho ảnh hiện đúng trên màng lưới.
+ Khi mắt ở trạng thái không điều tiết, tiêu cự của mắt lớn nhất (fmax, Dmin).
+ Khi mắt điều tiết tối đa, tiêu cự của mắt nhỏ nhất (fmin, Dmax).
2. Công thức – đơn vị đo
* Đặc điểm của mắt không bị tật (mắt bình thường)
+ Điểm cực cận CC cách mắt 25 cm = OCC = Đ
+ Điểm cực viễn CV ở vô cùng: CCV = ∞
+ Khoảng nhìn rõ của mắt [CC, CV]
Công thức tính độ tụ của mắt :
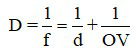
Trong đó:
+ D là độ tụ của mắt, có đơn vị dp;
+ d là khoảng cách từ vật đến mắt, có đơn vị mét (m);
+ OV là khoảng cách từ mắt đến võng mạc, có đơn vị mét (m).
Khi quan sát vật ở vô cùng (mắt không điều tiết ), d = ∞ thì độ tụ của mắt là
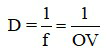
Khi quan sát vật ở điểm cực cận (mắt phải điều tiết tối đa), d = OCC thì độ tụ của mắt là
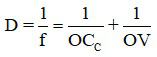
Khi chuyển từ trạng thái quan sát vật cách mắt d1 sang trạng thái quan sát vật ở vị trí cách mắt d2 thì độ biến thiên độ tụ của mắt là
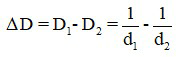
Khi chuyển từ trạng thái không điều tiết sang điều tiết tối đa
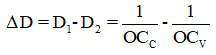
3. Mở rộng
Với mắt có tật cận thị
- Chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm trước màng lưới.
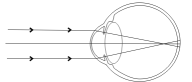
- fmax < OV nên Dmin > D0min
Với mặt có tật viễn thị
- Chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm sau màng lưới.
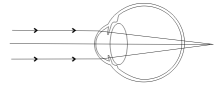
- fmax > OV nên Dmin < D0min
Khi đeo một thấu kính sát mắt, ta coi là một hệ hai thấu kính đồng trục ghép sát. Độ tụ của thấu kính tương đương bởi công thức:
D = D1 + D2
Trong đó:
+ D là độ tụ thấu kính tương đương, có đơn vị dp;
+ D1 và D2 lần lượt là độ tụ của các thấu kính đang đeo và mắt trong hệ ghép sát đồng trục, có đơn vị dp.
4. Bài tập ví dụ
Bài 1. Một người có mắt bình thường, nhìn được các vật ở rất xa mà không phải điều tiết. Khoảng cực cận của người này là OCC = 25 cm. Độ tụ của mắt người này khi điều tiết tối đa tăng thêm bao nhiêu?
Bài giải:
Ta có:
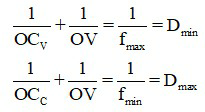
Lấy Dmax – Dmin = ∆D = 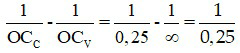 = 4 (dp)
= 4 (dp)
Đáp án: ∆D = 4dp.
Bài 2: Một người bị cận thị có khoảng cực viễn là OCV = 1 m. Biết khoảng cách từ thể thủy tinh đến võng mạc là 2,5 cm. Hỏi người này phải đeo sát mắt một thấu kính có độ tụ là bao nhiêu để có thể nhìn rõ vật ở xa vô cùng mà không cần điều tiết.
Bài giải:
Khi mắt nhìn xa vô cùng mà không cần điều tiết thì ảnh của vật hiện lên võng mạc, độ tụ của hệ mắt – thấu kính ghép sát là:
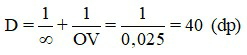
Nếu không đeo kính thì độ tụ của mắt là
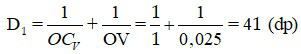
Áp dụng công thức tính độ tụ của hệ thấu kính đồng trục ghép sát:
D = D1 + D2 ⇒ D2 = D – D1 = 40 – 41 = -1 (dp)
Vậy thấu kính cần đeo có độ tụ là D2 = - 1 dp, là thấu kính phân kì.
Đáp án: Thấu kính cần đeo có độ tụ là -1 dp.
Công thức tính độ tụ của kính lúp hay, chi tiết
1. Định nghĩa
- Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ, được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cỡ cm). Kính lúp có tác dụng tạo ảnh với góc trông lớn hơn góc trông vật nhiều lần.

- Độ tụ là đại lượng vật lý đặc trưng cho khả năng hội tụ ánh sáng của thấu kính.
2. Công thức – đơn vị đo
Công thức độ tụ: D = 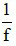
Trong đó:
+ D là độ tụ
+ f là tiêu cự của kính lúp, có đơn vị là mét (m).
Đơn vị của độ tụ là điôp, kí hiệu là dp : 1 dp = 1 m-1.
Vì kính lúp là thấu kính hội tụ nên D > 0.
3. Mở rộng
Khi biết độ tụ của kính lúp, ta có thể tính được tiêu cự của kính: f = 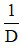
Khi biết vị trí vật và ảnh của vật tạo bởi thấu kính, ta có thể xác định độ tụ của thấu kính bởi công thức thấu kính:
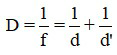
Trong đó:
+ D là độ tụ của thấu kính, có đơn vị dp;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét (m);
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét (m).
4. Bài tập ví dụ
Bài 1:
Một kính lúp có tiêu cự f = 5 cm. Tính độ tụ của kính
Bài giải:
Áp dụng công thức D = 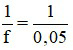 = 20 (dp)
= 20 (dp)
Đáp án: D = 20 dp
Bài 2: Một học sinh có điểm cực cận cách mắt 15 cm dùng kính lúp để quan sát các vật nhỏ. Khi đặt vật trước kính 2,5 cm thì ảnh hiện ra tại cực cận của mắt. Mắt đặt cách kính 10 cm. Hãy tính tiêu cự của kính lúp này.
Bài giải:
Ảnh ảo hiện ra ở cực cận cách mắt 15 cm, mà kính đặt cách mắt 10 cm, nên ảnh này cách kính 5 cm, ta có d’ = - 5cm = - 0,05 m.
Vật đặt trước kính 2,5 cm nên d = 2,5 cm = 0,025 m.
Áp dụng công thức thấu kính, ta có:
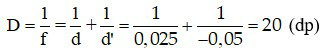
Đáp án: D = 20 dp.
Công thức tính số bội giác của kính lúp khi ngắm chừng vô cực hay, chi tiết
1. Định nghĩa
- Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ.
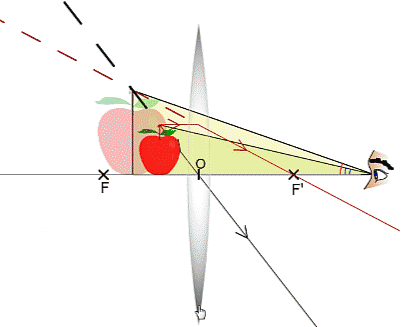
- Kính lúp được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cỡ cm), có tác dụng tạo ảnh với góc trông lớn hơn góc trông vật nhiều lần.
Cách sử dụng kính lúp
+ Đặt vật trong khoảng từ quang tâm O đến tiêu điểm vật chính F của kính lúp để có ảnh ảo cùng chiều và lớn hơn vật.
+ Ngắm chừng: điều chỉnh khoảng cách từ vật đến thấu kính để ảnh hiện ra trong giới hạn nhìn rõ của mắt.
+ Khi cần quan sát trong một thời gian dài, ta nên thực hiện cách ngắm chừng ở cực viễn để mắt không bị mỏi.
- Số bội giáclà đại lượng đặc trưng cho các dụng cụ quang học bổ trợ cho mắt, được xác định bằng thương số giữa góc trông ảnh qua dụng cụ quang học và góc trông trực tiếp vật:
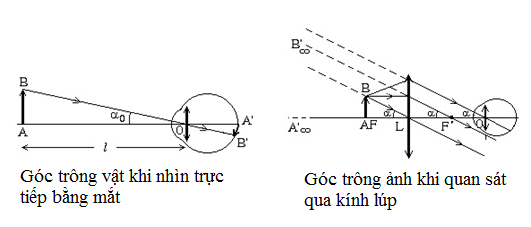
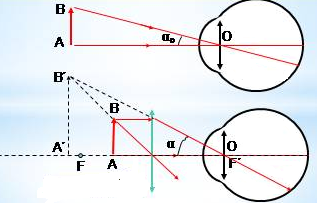
Góc trông vật khi nhìn trực tiếp
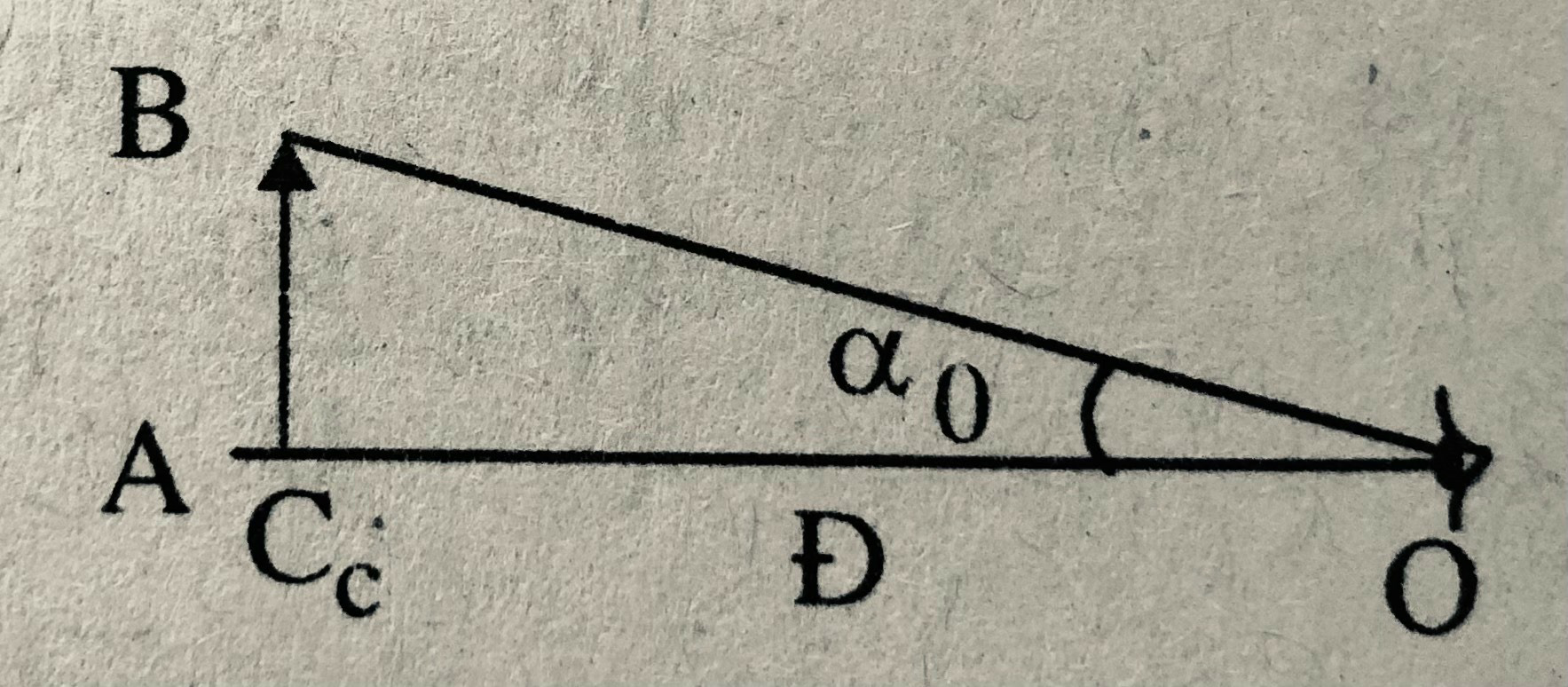
Góc trông vật khi nhìn qua kính lúp
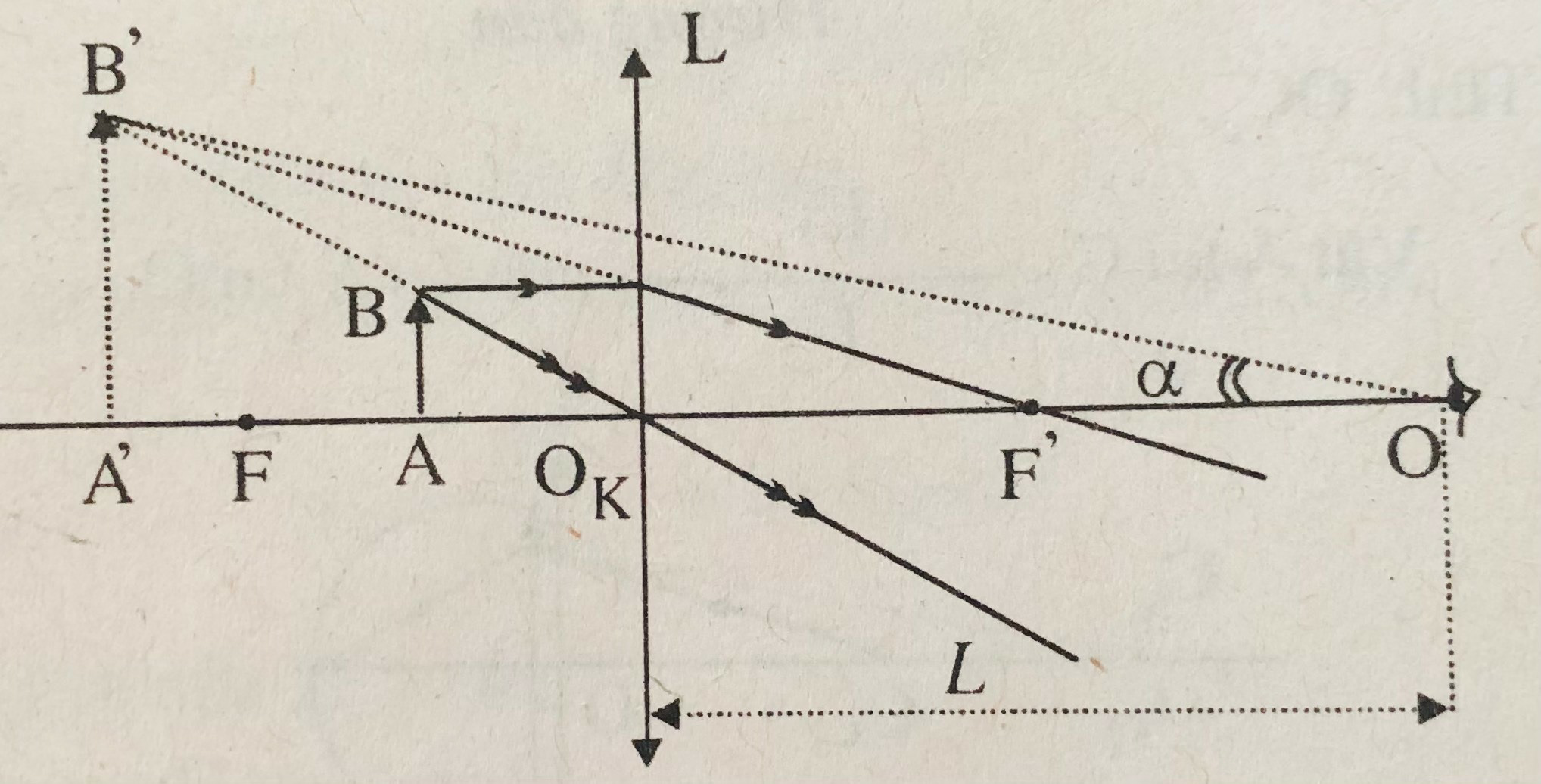
Sơ đồ tạo ảnh:
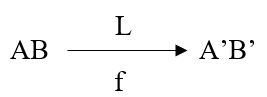
2. Công thức – đơn vị đo
- Khi ngắm chừng ở vô cực: G = 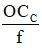
Trong đó:
+ f là tiêu cự của kính lúp, có đơn vị cm hoặc m.
+ OCC là khoảng cực cận của mắt, thường lấy là 25 cm = 0,25 m
+ G là số bội giác
3. Mở rộng
Trên thân kính lúp thường có ghi sẵn số bội giác (2x; 5x; 10x…)
Ví dụ: số 10X ở đây cho biết G = 10

Khi biết số bội giác của kính lúp, ta có thể xác định tiêu cự của kính lúp
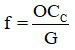
Trong đó:
+ G là số bội giác;
+ OCC là khoảng cực cận, thường lấy là 0,25 m.
+ f là tiêu cự của kính lúp, có đơn vị m
Khi biết độ tụ của kính lúp D = 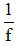 , ta có thể tính số bội giác khi ngắm chừng ở vô cực như sau:
, ta có thể tính số bội giác khi ngắm chừng ở vô cực như sau:
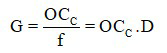
Trong đó:
+ G là số bội giác;
+ OCC là khoảng cực cận, thường lấy là 0,25 m.
+ f là tiêu cự của kính lúp, có đơn vị m.
+ D là độ tụ của kính lúp, có đơn vị dp.
4. Bài tập ví dụ
Bài 1: Một kính lúp có tiêu cự f = 5 cm. Tính số bội giác của kính lúp này khi ngắm chừng ở vô cực với mắt người bình thường, khoảng cực cận OCC = 25 cm.
Bài giải:
Áp dụng công thức G = 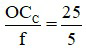 = 5
= 5
Đáp án: G = 5
Bài 2: Một kính lúp có độ tụ + 10 dp. Tính số bội giác của kính lúp này khi ngắm chừng ở vô cực với mắt người bình thường, khoảng cực cận OCC = 25 cm.
Bài giải:
Tiêu cự của kính lúp này là f = 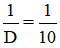 = 0,1m = 10cm
= 0,1m = 10cm
Số bội giác của kính lúp này là G = 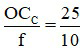 = 2,5
= 2,5
Đáp án: G = 2,5
Công thức tính số bội giác của kính lúp hay, chi tiết
1. Định nghĩa
- Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ, được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cỡ cm). Kính lúp có tác dụng tạo ảnh với góc trông lớn hơn góc trông vật nhiều lần.

- Cách sử dụng kính lúp
+ Đặt vật trong khoảng từ quang tâm O đến tiêu điểm vật chính F của kính lúp để có ảnh ảo cùng chiều và lớn hơn vật.
+ Ngắm chừng: điều chỉnh khoảng cách từ vật đến thấu kính để ảnh hiện ra trong giới hạn nhìn rõ của mắt.
+ Khi cần quan sát trong một thời gian dài, ta nên thực hiện cách ngắm chừng ở cực viễn để mắt không bị mỏi.
Số bội giáclà đại lượng đặc trưng cho các dụng cụ quang học bổ trợ cho mắt, được xác định bằng thương số giữa góc trông ảnh qua dụng cụ quang học và góc trông trực tiếp vật:
2. Công thức – đơn vị đo
Số bội giác được định nghĩa là: G = 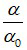
Vì các góc α và α0 đều rất nhỏ, nên ta có thể xác định
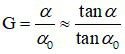
Mà góc trông vật α0 có giá trị lớn nhất khi vật đặt ở điểm cực cận (CC) nên
tanα0 = 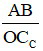 ; tan α =
; tan α = 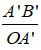
- Công thức tổng quát cho các trường hợp: 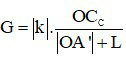
* Khi ngắm chừng ở cực cận: OA’ = OCC nên 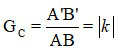
* Khi ngắm chừng ở cực viễn: OA’ = OCV nên 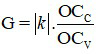
Trong đó:
+ α0 là góc trông khi nhìn trực tiếp bằng mắt khi vật đặt tại điểm cực cận;
+ α là góc trông ảnh khi nhìn qua kính lúp.
+ G là số bội giác
+ k là số phóng đại ảnh
+ L là khoảng cách từ kính lúp tới mắt
3. Mở rộng
Đối với người có mắt tốt, cực viễn ở vô cùng, vì vậy, số bội giác khi ngắm chứng ở vô cực được tính bằng công thức:
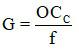 (với f là tiêu cự kính lúp)
(với f là tiêu cự kính lúp)
4. Bài tập ví dụ
Bài 1: Một người có điểm cực cận cách mắt 25 cm, sử dụng một kính lúp có tiêu cự f = 5 cm để quan sát một vật nhỏ. Kính đặt cách mắt 10 cm. Tính số bội giác của kính lúp khi ngắm chừng ở cực cận.
Bài giải:
Vì kính đặt cách mắt 10 cm nên ảnh hiện ra ở cực cận cách mắt 15 cm, ta có d’ = -15 cm.
Áp dụng công thức thấu kính: 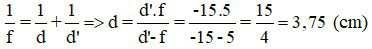
Khi ngắm chừng ở cực cận: OA’ = OCC nên 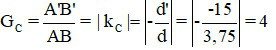
Đáp án: GC = 4
Bài 2: Một người mắt tốt có thể nhìn xa vô cùng mà không cần điều tiết, sử dụng một kính lúp có tiêu cự f = 2,5 cm để quan sát một vật nhỏ. Biết khoảng cực cận của mắt người này là 25 cm. Tính số bội giác khi ngắm chừng ở vô cực.
Bài giải:
Áp dụng công thức 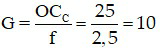
Đáp án: G = 10
Công thức tính số bội giác của kính hiển vi hay, chi tiết
1. Định nghĩa
+ Kính hiển vi là dụng cụ quang học bổ trợ cho mắt để nhìn các vật rất nhỏ, bằng cách tạo ra ảnh có góc trông lớn. Số bội giác của kính hiển vi lớn hơn nhiều so với số bội giác của kính lúp.
+ Kính hiển vi gồm vật kính L1 là thấu kính hội tụ có tiêu rất nhỏ (vài mm) và thị kính L2 là một kính lúp dùng để quan sát ảnh tạo bởi vật kính.
L1 và L2 đặt đồng trục; với O1O2 = ℓ không đổi. Khoảng cách F1’F2 = δ gọi là độ dài quang học của kính.
Ngoài ra còn có bộ phận tụ sáng để chiếu sáng vật cần quan sát. Đó thường là một gương cầu lõm.
Sơ đồ tạo ảnh:
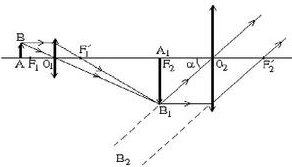
Cách sử dụng kính hiển vi
Sơ đồ tạo ảnh :
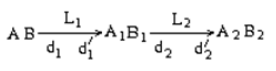
A1B1 là ảnh thật lớn hơn nhiều so với vật AB. A2B2 là ảnh ảo lớn hơn nhiều so với ảnh trung gian A1B1.
Mắt đặt sau thị kính để quan sát ảnh ảo A2B2.
Điều chỉnh khoảng cách từ vật đến vật kính (d1) sao cho ảnh cuối cùng (A2B2) hiện ra trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn hoặc bằng năng suất phân li của mắt.
Nếu ảnh sau cùng A2B2 của vật quan sát được tạo ra ở vô cực thì ta có sự ngắm chừng ở vô cực.
2. Công thức – đơn vị đo
- Số bội giác: 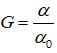
Ngắm chừng: dịch chuyển vật kính trước vật để ảnh ảo A’B’ ở trong khoảng thấy rõ của mắt:
Trường hợp tổng quát: 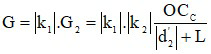
Xét trường hợp ngắm chừng ở vô cực. Số bội giác của kính hiển vi được xác định bởi công thức:
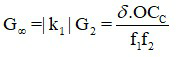
Trong đó:
+ G∞ là số bội giác của kính hiển vi khi ngắm chừng ở vô cực.
+ k1 là số phóng đại ảnh của vật kính L1
+ k2 là số phóng đại ảnh của thị kính L2
+ G2 là số bội giác khi ngắm chừng ở vô cực của thị kính L2
+ δ = F1’F2 = O1O2 – f1 – f2 là độ dài quang học của kính
+ f1 là tiêu cự của vật kính L1
+ f2 là tiêu cực của thị kính L2.
+ OCC là khoảng cực cận của mắt người quan sát, thường lấy bằng 25 cm.
+ L là khoảng cách từ thị kính tới mắt.
3. Mở rộng
Khi ngắm chừng ở cực cận thì 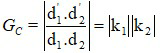
4. Bài tập ví dụ
Bài 1:
Một kính hiển vi có các tiêu cự vật kính và thị kính là f1 = 1 cm và f2 = 4 cm. Độ dài quang học của kính là 16 cm. Người quan sát có mắt không bị tật và có khoảng cực cận là OCC = 20 cm. Tính số bội giác khi ngắm chừng ở vô cực.
Bài giải:
Áp dụng công thức 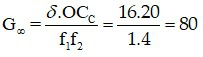
Đáp án: G∞ = 80
Bài 2: Một kính hiển vi có các tiêu cự vật kính và thị kính là f1 = 1 cm và f2 = 5 cm. Độ dài quang học của kính là 15 cm. Người quan sát có mắt không bị tật và có khoảng cực cận là OCC = 25 cm. Tính số bội giác khi ngắm chừng ở vô cực.
Bài giải:
Áp dụng công thức 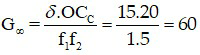
Đáp án: G∞ = 60
Công thức tính số bội giác của kính thiên văn hay, chi tiết
1. Định nghĩa
Kính thiên văn là dụng cụ quang bổ trợ cho mắt, có tác dụng tạo ảnh có góc trông lớn đối với các vật ở xa.
Kính thiên văn gồm:
+ Vật kính L1 là thấu kính hội tụ có tiêu cự dài (và dm đến vài m).
+ Thị kính L2 là thấu kính hội tụ có tiêu cự ngắn (vài cm).
Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng thay đổi được.

Sơ đồ tạo ảnh bởi kính thiên văn
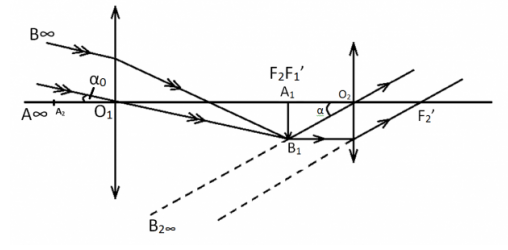
Cách ngắm chừng bởi kính thiên văn
Hướng trục của kính thiên văn đến vật AB ở rất xa cần quan sát để thu ảnh thật A1B1 trên tiêu diện ảnh của vật kính. Sau đó thay đổi khoảng cách giữa vật kính và thị kính để ảnh cuối cùng A2B2 qua thị kính là ảnh ảo, nằm trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn năng suất phân li của mắt.
Mắt đặt sau thị kính để quan sát ảnh ảo này.
Để có thể quan sát trong một thời gian dài mà không bị mỏi mắt, ta phải đưa ảnh cuối cùng ra vô cực: ngắm chừng ở vô cực.
2. Công thức – đơn vị đo
Trường hợp tổng quát: 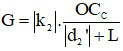
Khi ngắm chừng ở vô cực: 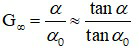
Ta có: tanα0 = 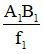 ; tanα =
; tanα = 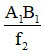
(mỗi thiên thể có góc trông α0 nhất định)
Do đó: G∞ = 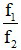
Trong đó :
+ G∞ là số bội giác khi ngắm chừng ở vô cực
+ f1 là tiêu cự của vật kính
+ f2 là tiêu cự của thị kính
Số bội giác của kính thiên văn trong điều kiện này không phụ thuộc vị trí đặt mắt sau thị kính.
3. Mở rộng
Khi biết số bội giác, ta có thể xác định tiêu cự của thị kính
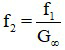
Ta có thể xác định tiêu cự của vật kính f1 = f2.G∞
4. Bài tập ví dụ
Bài 1: Vật kính của một kính thiên vắn có tiêu cự f1 = 1,2 mét, thị kính là một kính lúp có tiêu cự f2 = 4 cm. Tính số bội giác của kính thiên văn này khi ngắm chừng ở vô cực.
Bài giải:
Áp dụng công thức 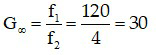
Đáp án: G = 30
Bài 2: Mắt một người không có tật dùng kính thiên văn quan sát mặt Trăng mà không cần điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 90 cm và số bội giác G∞ = 17.
Bài giải:
Khoảng cách giữa vật kính và thị kính là f1 + f2 = 90 (cm) (*)
Số bội giác khi ngắm chừng ở vô cực là G∞ = 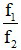 = 17 ⇒ f1 = 17f2
= 17 ⇒ f1 = 17f2
Thay vào (*) ta được f2 +17f2 = 90 ⇒ f2 = 5 cm
⇒ f1 = 90 – f2 = 85 cm.
Đáp án: f1 = 85 cm; f2 = 5 cm.
Công thức tính ảnh ảo của thấu kính hội tụ hay, chi tiết
1. Định nghĩa
- Thấu kính hội tụ hay còn gọi là thấu kính lồi, có rìa mỏng. Thấu kính có tác dụng khi các chùm tia sáng song song đi qua kính sẽ được hội tụ tại một tâm nhất định tùy theo hình dạng của thấu kính.
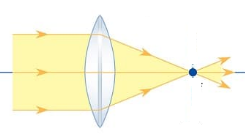
- Đường truyền của các tia sáng đặc biệt khi qua thấu kính hội tụ:
+ Tia tới đi qua quang tâm O cho tia ló tiếp tục truyền thẳng.
+ Tia tới song song với trục chính cho tia ló đi qua tiêu điểm F' của thấu kính.
+ Tia tới đi qua tiêu điểm F cho tia ló song song với trục chính của thấu kính
- Thấu kính hội tụ có các trường hợp tạo ảnh như sau:
|
Khoảng cách từ vật đến thấu kính (d) |
Đặc điểm của ảnh |
|||
|
Vật ở rất xa thấu kính |
thật |
ngược chiều |
nhỏ hơn vật |
|
|
d > 2f |
thật |
ngược chiều |
nhỏ hơn vật |
|
|
d = 2f |
thật |
ngược chiều |
bằng vật |
|
|
f < d < 2f |
thật |
ngược chiều |
lớn hơn vật |
|
|
d < f |
ảo |
cùng chiều |
lớn hơn vật |
|
|
d = f |
|
|
ảnh ở vô cực |
|
Chú ý:
+ Ảnh ảo không hiện được trên màn nhưng có thể nhìn thấy bằng mắt khi mắt đặt sau thấu kính để nhận chùm tia ló.
+ Ảnh thật có thể hiện rõ trên màn hoặc được nhìn thấy bằng mắt khi mắt đặt sau điểm hội tụ của chùm tia ló.
2. Công thức – đơn vị đo
Công thức xác định vị trí ảnh ảo tạo bởi thấu kính hội tụ:
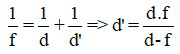
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị mét, với thấu kính hội tụ f > 0;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét, vì vật thật nên d > 0;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét, vì ảnh ảo nên d’< 0.
Công thức xác định chiều cao ảnh
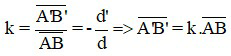
Trong đó:
+ k là số phóng đại ảnh, ảnh ảo nên k > 0 (ảnh cùng chiều với vật);
+ 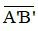 là chiều cao ảnh, có đơn vị mét;
là chiều cao ảnh, có đơn vị mét;
+ 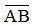 là chiều cao vật, có đơn vị mét;
là chiều cao vật, có đơn vị mét;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét, vì vật thật nên d > 0;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét, vì ảnh ảo nên d’ <0.
3. Mở rộng
Từ công thức xác định vị trí ảnh ta có thể xác định số phóng đại ảnh như sau:
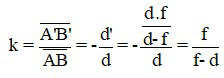
Khi biết vị trí ảnh và tiêu cự, ta có thể xác định vị trí vật như sau:
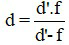
Khi biết vị trí vật và ảnh, ta có thể xác định tiêu cự như sau
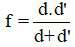
Trong đó:
+ k là số phóng đại ảnh, ảnh ảo nên k > 0 (ảnh cùng chiều với vật);
+ 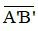 là chiều cao ảnh, có đơn vị mét;
là chiều cao ảnh, có đơn vị mét;
+ 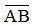 là chiều cao vật, có đơn vị mét;
là chiều cao vật, có đơn vị mét;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét, vì vật thật nên d > 0;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét, vì ảnh ảo nên d’ < 0.
+ f là tiêu cự của thấu kính, có đơn vị mét, với thấu kính hội tụ f > 0;
4. Bài tập ví dụ
Bài 1: Đặt vật sáng AB cao 2 cm trước một thấu kính hội tụ có tiêu cự f = 10 cm và cách thấu kính 5 cm. Tính chiều cao và vị trí ảnh.
Bài giải:
Vì vật thật nên d > 0, thấu kính hội tụ có f >0.
Áp dụng công thức tính vị trí ảnh: 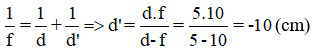
Vì d’ < 0 nên đây là ảnh ảo.
Áp dụng công thức số phóng đại ảnh:
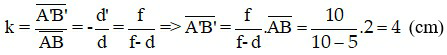
Đáp án: d’ = - 10 cm; A’B’ cao 4 cm.
Bài 2: Một vật sáng AB đặt trước thấu kính và cách thấu kính 20 cm, cho ảnh ảo cách thấu kính 60 cm. Tính tiêu cự của kính. Đây là thấu kính loại gì?
Bài giải:
Vì vật thật nên d = 20 cm; ảnh ảo nên d’ = - 60 cm
Áp dụng công thức 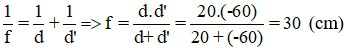
Đây là thấu kính hội tụ
Đáp án: f = 30 cm
Công thức tính ảnh ảo hay, chi tiết
1. Định nghĩa
- Thấu kính hội tụ hay còn gọi là thấu kính lồi, có rìa mỏng. Thấu kính có tác dụng khi các chùm tia sáng song song đi qua kính sẽ được hội tụ tại một tâm nhất định tùy theo hình dạng của thấu kính.
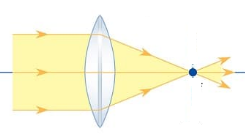
- Đường truyền của các tia sáng đặc biệt khi qua thấu kính hội tụ:
+ Tia tới đi qua quang tâm O cho tia ló tiếp tục truyền thẳng.
+ Tia tới song song với trục chính cho tia ló đi qua tiêu điểm F' của thấu kính.
+ Tia tới đi qua tiêu điểm F cho tia ló song song với trục chính của thấu kính
- Thấu kính phân kì hay còn gọi là thấu kính lõm, có rìa dày. Thấu kính có tác dụng làm phân kì chùm sáng song song đi qua thấu kính.
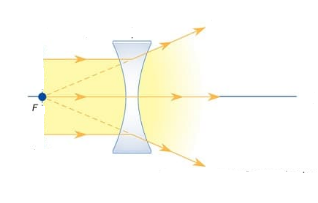
- Đường truyền của các tia sáng đặc biệt khi qua thấu kính phân kì:
+ Tia tới đi qua quang tâm O cho tia ló tiếp tục truyền thẳng.
+ Tia tới song song với trục chính cho tia ló có đường kéo dài đi qua tiêu điểm F' của thấu kính.
+ Tia tới có đường kéo dài đi qua tiêu điểm F cho tia ló song song với trục chính của thấu kính
Các trường hợp tạo ảnh của hai loại thấu kính (chỉ xét vật thật)
|
Ảnh |
Thấu kính hội tụ f > 0 |
Thấu kính phân kì f <0 |
|
OI = OI’ = 2f |
|
|
|
Tính chất ảnh |
Ảnh thật khi vật nằm ngoài OF Ảnh ảo khi vật nằm trong OF |
Ảnh luôn luôn ảo |
|
Độ lớn của ảnh so với vật |
Ảnh ảo > vật Ảnh thật > vật khi vật nằm trong FI Ảnh thật = vật khi vật ở I (ảnh ở I’) Ảnh thật < vật khi vật ngoài FI |
Ảnh < vật |
|
Chiều của ảnh so với vật |
Ảnh thật ngược chiều với vật Ảnh ảo cùng chiều với vật |
Ảnh cùng chiều so với vật |
2. Công thức – đơn vị đo
Công thức xác định vị trí ảnh bởi thấu kính:
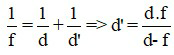
Trong đó:
+ f là tiêu cự của thấu kính, có đơn vị mét;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét.
Công thức xác định chiều cao ảnh
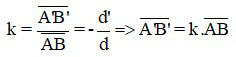
Trong đó:
+ k là số phóng đại ảnh, ảnh ảo nên k > 0 (ảnh cùng chiều với vật);
+ 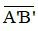 là chiều cao ảnh, có đơn vị mét;
là chiều cao ảnh, có đơn vị mét;
+ 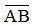 là chiều cao vật, có đơn vị mét;
là chiều cao vật, có đơn vị mét;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét;
+ f là tiêu cự của thấu kính, có đơn vị mét.
Quy ước về dấu:
|
Tên đại lượng |
Kí hiệu |
Quy ước dấu |
|
Tiêu cự |
f |
Thấu kính hội tụ: f > 0 Thấu kính phân kì: f <0 |
|
Khoảng cách từ vật đến TK |
|
Vật thật: d >0 Vật ảo: d < 0 |
|
Khoảng cách từ ảnh đến TK |
|
Ảnh thật: d’ >0 Ảnh ảo: d’ <0 |
|
Số phóng đại ảnh |
|
Ảnh > vật : |k| >1 Ảnh < vật: |k| <1 Ảnh = vật: |k| = 1 Ảnh cùng chiều vật: k > 0 Ảnh ngược chiều vật: k < 0 |
3. Mở rộng
Khi biết số phóng đại ảnh, ta có thể xác định liên hệ giữa vị trí ảnh và vị trí vật
d' = -k.d
Kết hợp công thức xác định vị trí ảnh và vị trí vật, ta có thể xác định số phóng đại ảnh bởi công thức:
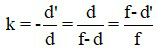
Khi biết số phóng đại ảnh và chiều cao ảnh, ta tính được chiều cao vật
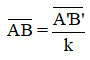
4. Bài tập ví dụ
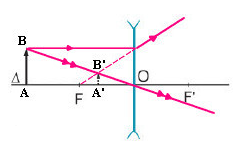
Bài 1: Một vật sáng AB đặt trước thấu kính phân kì có tiêu cự f = - 10 cm và cách thấu kính 20 cm. Xác định vị trí ảnh ?
Bài giải:
Vì vật thật nên d = 20 cm; thấu kính phân kì f = - 10 cm
Áp dụng công thức 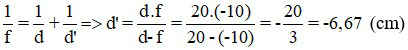
Đáp án: d’ = - 6,67 cm
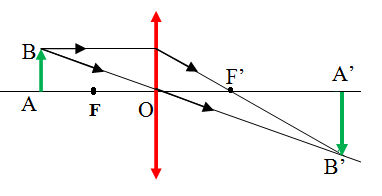
Bài 2: Một thấu kính hội tụ có tiêu cự f = 20 cm cho ảnh thật cao gấp 2 lần vật. Xác định vị trí vật và ảnh.
Bài giải:
Vì ảnh thật cao gấp hai lần vật nên k = - 2.
Ta có 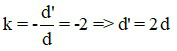
Áp dụng công thức xác định vị trí ảnh:
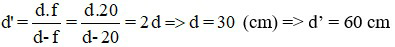
Đáp án: d = 30 cm; d’ = 60 cm.
Công thức tính hệ số phóng đại hay, chi tiết
1. Định nghĩa
Hệ số phóng đại cho ta biết ảnh có độ lớn gấp bao nhiêu lần vật, được tính bằng tỉ số giữa chiều cao của ảnh và chiều cao của vật, được kí hiệu là k.
2. Công thức – đơn vị đo
Công thức số phóng đại ảnh
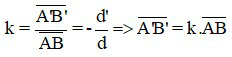
Trong đó:
+ k là số phóng đại ảnh, ảnh ảo nên k > 0 (ảnh cùng chiều với vật);
+ 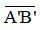 là chiều cao ảnh, có đơn vị mét;
là chiều cao ảnh, có đơn vị mét;
+ 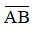 là chiều cao vật, có đơn vị mét;
là chiều cao vật, có đơn vị mét;
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét;
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét;
+ f là tiêu cự của thấu kính, có đơn vị mét.
Quy ước:
+ Thấu kính hội tụ: f > 0; thấu kính phân kì: f < 0
+ vật thật: d > 0; vật ảo: d < 0;
+ ảnh thật: d’ > 0; ảnh ảo: d’ < 0
+ ảnh lớn hơn vật: |k| > 1; ảnh nhỏ hơn vật thì |k| < 1
+ ảnh ảo cùng chiều với vật: k > 0; ảnh thật ngược chiều với vật: k < 0.
3. Mở rộng
Kết hợp công thức thấu kính để xác định vị trí ảnh và vị trí vật, ta có thể xác định số phóng đại ảnh bởi công thức:
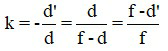
Khi biết số phóng đại ảnh, ta có thể tính được chiều cao ảnh, hoặc chiều cao vật
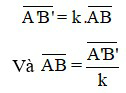
Khi biết số phóng đại ảnh, ta có thể xác định tỉ số giữa khoảng cách từ ảnh đến thấu kính với khoảng cách từ vật đến thấu kính
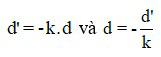
Đối với hệ hai thấu kính đồng trục ghép sát, thì số phóng đại ảnh được xác định như sau :
+ Hệ hai thấu kính đồng trục ghép cách nhau một khoảng ℓ.
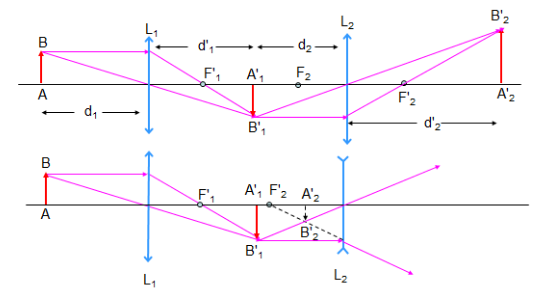
Sơ đồ tạo ảnh:
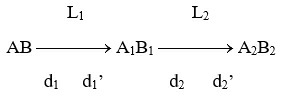
Với: d2 = O1O2 – d1’; k = k1k2 = 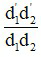
+ Hệ hai thấu kính đồng trục ghép sát nhau
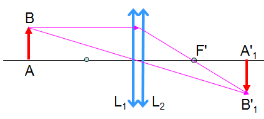
Sơ đồ tạo ảnh:
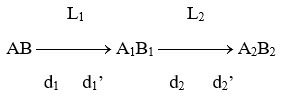
Với: d2 = – d1’; k = k1k2 = 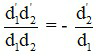
Lưu ý: Trong nhiều bài tập không chỉ rõ k > 0 hay k < 0 mà chỉ cho biết ảnh cao gấp bao nhiêu lần vật, khi đó ta cần căn cứ vào tính thật, ảo hoặc tính cùng chiều, ngược chiều giữa ảnh và vật để xác định giá trị của k.
+ ảnh lớn hơn vật: |k| > 1; ảnh nhỏ hơn vật thì |k| < 1
+ ảnh ảo cùng chiều với vật: k > 0; ảnh thật ngược chiều với vật: k < 0.
4. Bài tập ví dụ
Bài 1: Một vật sáng AB đặt trước thấu kính phân kì có tiêu cự f = - 10 cm và cách thấu kính 20 cm. Xác định vị trí ảnh và số phóng đại ảnh ?
Bài giải:
Vì vật thật nên d = 20 cm; thấu kính phân kì f = - 10 cm
Áp dụng công thức 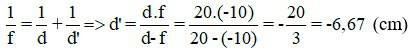
Số phóng đại ảnh là 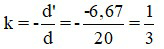
Đáp án: d’ = -6,67 cm; k = 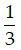
Bài 2: Một thấu kính hội tụ có tiêu cự f = 20 cm cho ảnh thật cao gấp 2 lần vật. Xác định vị trí vật và ảnh.
Bài giải:
Vì ảnh thật cao gấp hai lần vật nên k = - 2.
Ta có 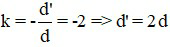
Áp dụng công thức xác định vị trí ảnh:
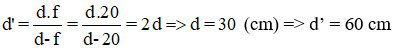
Đáp án: d = 30 cm; d’ = 60 cm.
Công thức tính khoảng cách từ vật đến ảnh hay, chi tiết
1. Định nghĩa
Khoảng cách giữa vật và ảnh được kí hiệu là L, được định nghĩa L = AA’, có đơn vị mét.
2. Công thức – đơn vị đo
Công thức tính khoảng cách từ vật đến ảnh: L = |d + d’| = 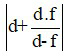
Trong đó:
+ L là khoảng cách từ vật đến ảnh, có đơn vị mét (m);
+ d là khoảng cách từ vật đến thấu kính, có đơn vị mét (m);
+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị mét (m);
+ f là tiêu cự của thấu kính, có đơn vị mét (m).
3. Mở rộng
Trường hợp thấu kính hội tụ tạo ảnh thật thì d > 0 và d’ > 0 nên L = d +d’
Trường hợp thấu kính hội tụ tạo ảnh ảo thì d > 0 và d’< 0 nhưng |d’| > d nên
L = - d’ – d
Trường hợp thấu kính phân kì tạo ảnh ảo thì d > 0 và d’ < 0, nhưng |d’| < d nên
L = d + d’
4. Bài tập ví dụ
Bài 1: Một vật sáng AB đặt trước thấu kính phân kì có tiêu cự f = - 10 cm và cách thấu kính 30 cm. Xác định vị trí ảnh và khoảng cách giữa vật và ảnh ?
Bài giải:
Vì vật thật nên d = 30 cm; thấu kính phân kì f = - 10 cm
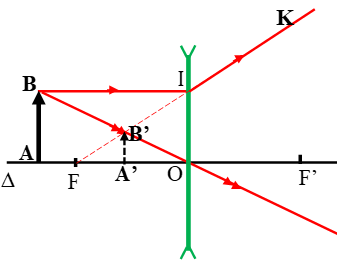
Áp dụng công thức 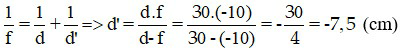
Khoảng cách giữa vật và ảnh là:
L = |d+d’|= |30 – 7,5 | = 22,5 (cm)
Đáp án: L = 22,5 cm
Bài 2: Một thấu kính hội tụ có tiêu cự f = 20 cm cho ảnh thật cao gấp 2 lần vật. Xác định khoảng cách giữa vật và ảnh.
Bài giải:
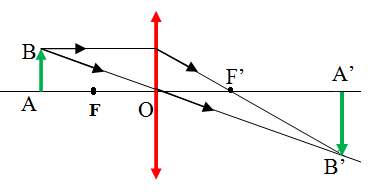
Vì ảnh thật cao gấp hai lần vật nên k = - 2.
Ta có k = 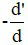 = -2 ⇒ d' = 2d
= -2 ⇒ d' = 2d
Áp dụng công thức xác định vị trí ảnh:
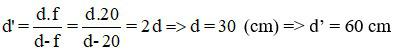
Khoảng cách giữa vật và ảnh là L = |d+d’|= |30+60| = 90 cm
Đáp án: L = 90 cm.
Công thức tính khoảng cách từ vật đến thấu kính hay, chi tiết
1. Định nghĩa
Khoảng cách từ vật đến thấu kính là d = OA, được quy ước như sau:
+ vật thật: d >0
+ vật ảo: d < 0
2. Công thức – đơn vị đo
Trường hợp đối với một thấu kính
Công thức tính khoảng cách từ vật đến thấu kính :
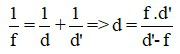
3. Mở rộng
Khi biết số phóng đại ảnh là k, ta có thể xác định tỉ số giữa khoảng cách từ vật đến thấu kính và khoảng cách từ ảnh đến thấu kính
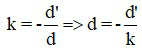
Đối với hệ thấu kính đồng trục L1, L2 có khoảng cách giữa hai tâm là O1O2 thì ảnh của L1 trở thành vật đối với thấu kính L2
Ví dụ: Hệ hai thấu kính hội tụ
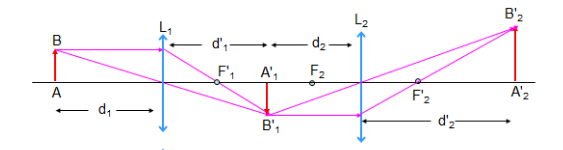
Hệ thấu kính hội tụ - phân kì
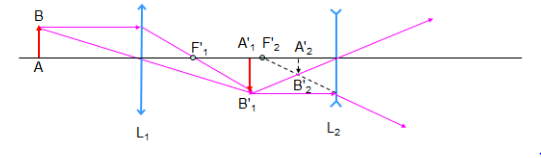
Ta có sơ đồ tạo ảnh
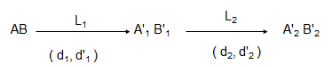
Khi đó khoảng cách từ vật sáng A1’B1’ đến thấu kính L2 là: d2 = O1O2 - d1’
Trong đó:
+ d2 là khoảng cách từ ảnh của vật AB tạo bởi thấu kính L1, nay là vật sáng đối với L2 đến thấu kính L2.
+ d1’ là khoảng cách từ ảnh của vật AB tạo bởi thấu kính L1 đến thấu kính L1
+ O1O2 là khoảng cách giữa hai quang tâm của hai thấu kính.
Lưu ý: nếu hệ thấu kính ghép sát thì O1O2 = 0, khi đó d2 = -d1’
4. Bài tập ví dụ
Bài 1: Một thấu kính hội tụ có tiêu cự f = 20 cm cho ảnh thật cao gấp 2 lần vật. Xác định khoảng cách giữa vật và thấu kính.
Bài giải:
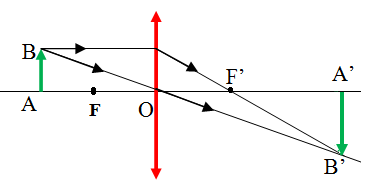
Vì ảnh thật cao gấp hai lần vật nên k = - 2.
Ta có k = 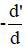 = -2 ⇒ d' = 2d
= -2 ⇒ d' = 2d
Áp dụng công thức xác định vị trí ảnh:
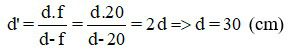
Đáp án: d = 30 cm.
Bài 2: Cho thấu kính hội tụ L2 có tiêu cự f2 = 24 cm và vật AB đặt trên trục chính cách thấu kính một đoạn không đổi a = 44 cm. Thấu kính phân kì L1 có tiêu cự f1 = - 15 cm được đặt giữa vật AB và L2, cách L2 một khoảng ℓ sao cho hai trục chính trùng nhau. Xác định vị trí và số phóng đại k của ảnh sau cùng A2’B2’ trong trường hợp ℓ = 34 cm
Bài giải
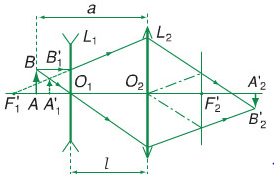
Sơ đồ tạo ảnh:
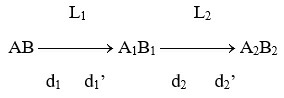
Ta có d’1 = 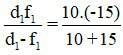 = - 6 (cm)
= - 6 (cm)
d2 = ℓ – d’1 = 34 – (-6) = 40 (cm)
d’2 = 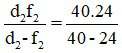 = 60 (cm)
= 60 (cm)
k = 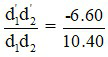 = - 0,9
= - 0,9
Ảnh cuối cùng là ảnh thật, ngược chiều với vật và cao bằng 0,9 lần vật.
Công thức về mắt hay, chi tiết
1. Định nghĩa
Mắt là một hệ gồm nhiều môi trường trong suốt tiếp giáp nhau bằng các mặt cầu.
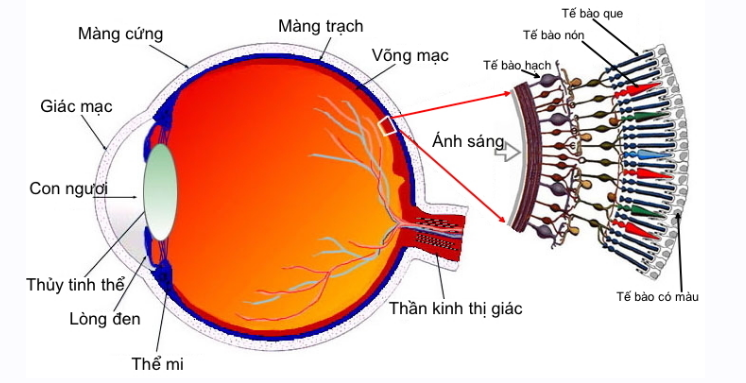
Từ ngoài vào trong, mắt có các bộ phận sau:
+ Giác mạc: Màng cứng, trong suốt. Bảo vệ các phần tử bên trong và làm khúc xạ các tia sáng truyền vào mắt.
+ Thủy dịch: Chất lỏng trong suốt có chiết suất xấp xỉ bằng chiết suất của nước.
+ Lòng đen: Màn chắn, ở giữa có lỗ trống gọi là con ngươi. Con ngươi có đường kính thay đổi tự động tùy theo cường độ sáng.
+ Thể thủy tinh: Khối chất đặc trong suốt có hình dạng thấu kính hai mặt lồi.
+ Dịch thủy tinh: Chất lỏng giống chất keo loãng, lấp đầy nhãn cầu sau thể thủy tinh.
+ Màng lưới (võng mạc): tại đó tập trung đầu các sợi dây thần kinh thị giác. Ở màng lưới có điểm vàng V là nơi cảm nhận ánh sáng nhạy nhất và điểm mù không nhạy cảm với ánh sáng.
Hệ quang học của mắt được coi tương đương một thấu kính hội tụ gọi là thấu kính mắt. Độ tụ của mắt là đại lượng vật lý đặc trưng cho khả năng hội tụ ánh sáng của mắt.
Khi nhìn các vật ở các khoảng cách khác nhau (d thay đổi) thì mắt sẽ điều tiết để thay đổi f của thấu kính mắt sao cho ảnh hiện đúng trên màng lưới.
+ Khi mắt ở trạng thái không điều tiết, tiêu cự của mắt lớn nhất (fmax, Dmin).
+ Khi mắt điều tiết tối đa, tiêu cự của mắt nhỏ nhất (fmin, Dmax).
+ Khi mắt không điều tiết, điểm trên trục của mắt mà ảnh tạo ra ngay tại màng lưới gọi là điểm cực viễn CV. Mắt không có tật CV ở xa vô cùng (OCV = ∞).
+ Khi mắt điều tiết tối đa, điểm trên trục của mắt mà ảnh còn được tạo ra ngay tại màng lưới gọi là điểm cực cận CC. Đó cũng là điểm gần nhất mà mắt còn nhìn rõ. Khoảng cách giữa CV và CC gọi là khoảng nhìn rõ của mắt. OCV gọi là khoảng cực viễn, Đ = OCC gọi là khoảng cực cận.
Năng suất phân li của mắt
+ Góc trông vật AB là góc tưởng tượng nối quang tâm của mắt tới hai điểm đầu và cuối của vật.
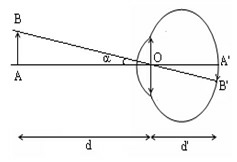
+ Góc trông nhỏ nhất ε = αmin giữa hai điểm để mắt còn có thể phân biệt được hai điểm đó gọi là năng suất phân li của mắt. Khi đó, ảnh của 2 điểm đầu và cuối của vật được tạo ra ở hai tế bào thần kinh thị giác kế cận nhau.
Mắt cận và cách khắc phục
- Độ tụ của mắt cận lớn hơn độ tụ mắt bình thường, chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm trước màng lưới.
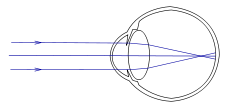
- fmax < OV.
- OCv hữu hạn.
- Không nhìn rõ các vật ở xa.
- Cc ở rất gần mắt hơn bình thường.
- Để khắc phục tật cận thị cần đeo thấu kính phân kì có độ tụ thích hợp để có thể nhìn rõ vật ở vô cực mà mắt không phải điều tiết.
Mắt viễn thị và cách khắc phục
- Độ tụ nhỏ hơn độ tụ của mắt bình thường, chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm sau màng lưới.
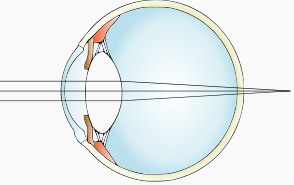
- fmax > OV.
- Nhìn vật ở vô cực phải điều tiết.
- Cc ở rất xa mắt hơn bình thường.
- Để khắc phục tật viễn thị cần đeo một thấu kính hội tụ có tụ số thích hợp để:
+ Nhìn rõ các vật ở xa mà không phải điều tiết mắt.
+ Hoặc nhìn rõ được vật ở gần như mắt bình thường (ảnh ảo của điểm gần nhất muốn quan sát qua thấu kính hiện ra ở điểm cực cận của mắt).
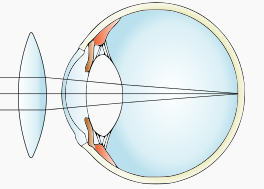
Mắt lão và cách khắc phục
+ Khi tuổi cao khả năng điều tiết giảm vì cơ mắt yếu đi và thể thủy tinh cứng hơn nên điểm cực cận CC dời xa mắt.
+ Để khắc phục tật lão thị, phải đeo kính hội tụ để nhìn rỏ vật ở gần như mắt bình thường.
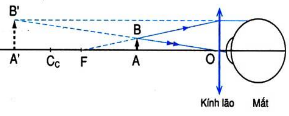
2. Công thức – đơn vị đo
Với mắt người bình thường, vật sáng ở trước mắt luôn cho ảnh hiện trên võng mạc, nên độ tụ của thể thủy tinh được xác định bằng công thức
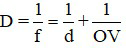
Trong đó:
+ D là độ tụ của mắt, có đơn vị dp;
+ d là khoảng cách từ vật đến mắt, có đơn vị mét (m);
+ OV là khoảng cách từ mắt đến võng mạc, có đơn vị mét (m).
Khi mắt nhìn vật ở cực viễn thì không cần điều tiết: 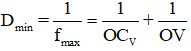
Với mắt tốt, CV ở vô cùng nên
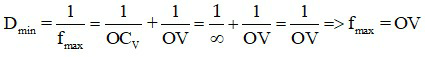
Khi mắt quan sát vật ở cực cận:
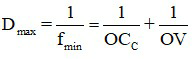
Khi chuyển trạng thái không điều tiết sang điều tiết tối đa thì độ tụ của mắt thay đổi một lượng là:
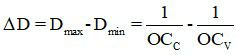
Công thức tính góc trông α của mắt: tanα = 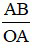
Mắt bình thường ε = αmin = 1’.
Mắt cận thị muốn nhìn các vật ở xa vô cùng mà không cần điều tiết cần đeo thấu kính phân kì có tiêu cự là : fk = - (OCV – L)
Trong đó:
+ L là khoảng cách từ kính đến mắt
+ OCV là khoảng cực viễn của mắt
Nếu kính đeo sát mắt thì L = 0, fK = - OCV
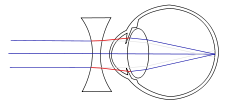
Mắt cận thị muốn nhìn các vật ở cách mắt 25 cm như người bình thường cần đeo thấu kính hội tụ có tiêu cự là :
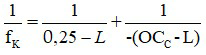
Trong đó:
+ L là khoảng cách từ kính đến mắt, có đơn vị mét
+ OCC là khoảng cực cận của mắt, có đơn vị mét
Nếu kính đeo sát mắt thì L = 0, 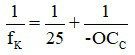
Mắt viễn thị muốn nhìn các vật ở cách mắt 25 cm như người bình thường cần đeo thấu kính hội tụ có tiêu cự là :
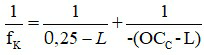
Trong đó:
+ L là khoảng cách từ kính đến mắt, có đơn vị mét
+ OCC là khoảng cực cận của mắt, có đơn vị mét
Nếu kính đeo sát mắt thì L = 0, 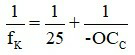
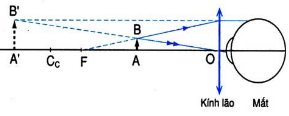
Mắt lão thị cần đeo kính để đọc được sách cách mắt 25 cm như người bình thường thì ảnh ảo của vật đặt tại điểm cực cận hiện ra ở cách mắt 25 cm, nên tiêu cự kính cần đeo là:
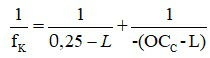
Trong đó:
+ L là khoảng cách từ kính đến mắt, có đơn vị mét
+ OCC là khoảng cực cận của mắt, có đơn vị mét
Nếu kính đeo sát mắt thì L = 0, 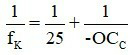
3. Mở rộng
Khi mắt đeo kính, ta coi hệ mắt – kính là một hệ quang học hai thấu kính ghép đồng trục. Ảnh ảo của vật qua thấu kính trở thành vật đối với mắt.
Áp dụng công thức thấu kính để xác định vị trí vật đối với mắt khi kính đeo sát mắt:
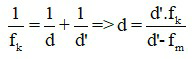
4. Bài tập ví dụ
Bài 1: Mắt của một người có điểm cực viễn cách mắt 50 cm.
a) Mắt người này mắc tật gì?
b) Muốn nhìn thấy vật ở vô cực mà không điều tiết, người đó phải đeo kính có độ tụ bao nhiêu? Biết kính đeo sát mắt
c) Điểm CC cách mắt 10 cm. Khi đeo kính, mắt nhìn thấy điểm gần nhất cách mắt bao nhiêu? (kính đeo sát mắt)
Bài giải:
a) Điểm cực viễn CV cách mắt một khoảng hữu hạn nên người này bị cận thị.
b) fK = - OCV = - 50 cm = - 0,5 m.
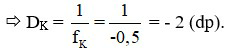
c) d’ = - OCC = - 10 cm.
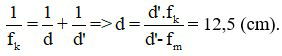
Bài 2: Một người đứng tuổi nhìn rõ được các vật ở xa. Muốn nhìn rõ vật gần nhất cách mắt 27 cm thì phải đeo kính có độ tụ + 2,5 dp cách mắt 2 cm.
a) Xác định các điểm cực cận và cực viễn của mắt.
b) Nếu đeo kính sát mắt thì có thể nhìn rõ các vật trong khoảng nào?
Bài giải:
a) Điểm cực viễn CV ở vô cực.
Ta có fK = 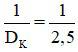 = 0,4(m) = 40 (cm).
= 0,4(m) = 40 (cm).
Khi đeo kính ta có d = OCCK – ℓ = 27- 2= 25 cm.
d’ = 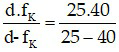 = - 66,7 (cm).
= - 66,7 (cm).
Mà d’ = - OCC + ℓ
⇒ OCC = - d’ + ℓ = 66,7 + 2 = 68,7 cm.
b) Đeo kính sát mắt
Khoảng cực viễn của mắt khi đeo kính là OCVK = fK = 40 cm.
Khoảng cực cận của mắt khi đeo kính là OCCK = 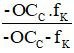 = 25,3 cm.
= 25,3 cm.
Công thức tính năng suất phân li của mắt hay, chi tiết
1. Định nghĩa
- Muốn cho mắt nhìn thấy một vật thì ảnh thật của vật tạo bởi mắt phải hiện ra ở màng lưới, nghĩa là vật phải có vị trí ở trong khoảng nhìn rõ của mắt. Tuy nhiên, trong nhiều trường hợp, ta muốn quan sát được các chi tiết nhỏ của vật. Việc nhìn thấy được một vật nhỏ AB tùy thuộc vào kích thước ảnh A’B’ của vật đó trên màng lưới. Kích thước này phụ thuộc góc trông vật.
- Góc trông nhỏ nhất ε = αmin giữa hai điểm để mắt còn có thể phân biệt được hai điểm đó gọi là năng suất phân li của mắt. Khi đó, ảnh của 2 điểm đầu và cuối của vật được tạo ra ở hai tế bào thần kinh thị giác kế cận nhau. Năng suất phân li thay đổi tùy theo từng người.
2. Công thức – đơn vị đo
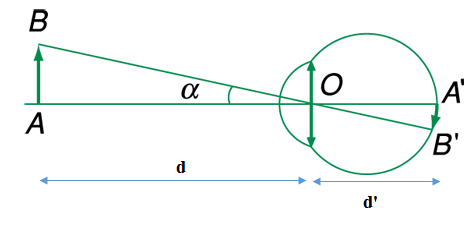
Công thức tính góc trông vật
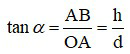
Trong đó:
+ α là góc trông vật,
+ AB = h là chiều cao vật, có đơn vị mét
+ OA = d là khoảng cách từ vật đến mắt, có đơn vị mét.
Khi d tăng thì góc α giảm.
Góc trông α nhỏ nhất để mắt còn phân biệt được hai điểm A, B gọi là năng suất phân li của mắt.
Giá trị trung bình của năng suất phân ly ε = αmin = 1’.
3. Mở rộng
Do ảnh hiện lên trên võng mạc, nên ta còn có thể tính góc trông khi biết chiều cao ảnh A’B’ như sau:
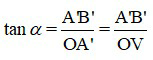
4. Bài tập ví dụ
Bài 1: Một người có mắt tốt, quan sát một cây cao 1,5 m ở phía trước mặt, cách mắt 20 mét. Tính góc trông cái cây này, so sánh với năng suất phân li của mắt là ε = 1’.

Bài giải:
Góc trông cái cây này là
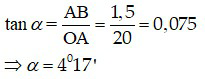
Góc trông này lớn hơn năng suất phân li rất nhiều lần, nên người này còn quan sát tốt cái cây.
Bài 2: Một người có mắt tốt ngồi trên đỉnh núi quan sát phía xa. Ở ngọn núi trước mặt có một bụi cây cao 0,5 m cách người quan sát 2 km. Hỏi người này có thể quan sát được rõ bụi cây này không? Biết năng suất phân li của mắt là ε = 1’.

Bài giải:
Góc trông vật khi quan sát bụi cây cao 0,5 m cách người quan sát 2 km là:
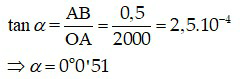
Người này không quan sát rõ được bụi cây này vì góc trông vật nhỏ hơn năng suất phân li của mắt.
Công thức Mắt và các dụng cụ quang học đầy đủ, chi tiết
I. Lý thuyết
1. Lăng kính là một khối chất trong suốt, đồng chất (thủy tinh, nhựa,…) thường có dạng lăng trụ tam giác.
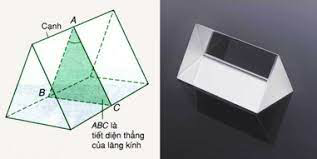
Một lăng kính được đặc trưng bởi góc chiết quang A và chiết suất n.
Tia sáng đơn sắc truyền qua lăng kính đặt trong môi trường chiết quang kém hơn thì tia ló bao giờ cũng lệch về phía đáy của lăng kính so với tia tới.
Góc tạo bởi tia ló và tia tới gọi là góc lệch D của tia sáng khi truyền qua lăng kính.
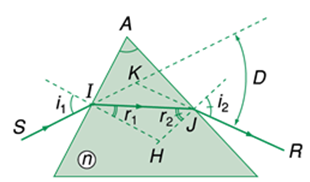
Lăng kính có thể phân tích chùm sáng phức tạp thành những thành phần đơn sắc.
Lăng kính là thành phần quan trọng của máy quang phổ

2. Thấu kính là một khối chất trong suốt giới hạn bởi hai mặt cong hoặc bởi một mặt cong và một mặt phẵng.
- Thấu kính lồi (rìa mỏng) có tác dụng hội tụ chùm tia sáng song song khi qua nó, gọi là thấu kính hội tụ:
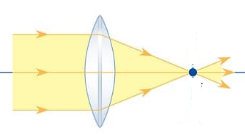
- Thấu kính lõm (có rìa dày) có tác dụng làm phân kì chùm sáng song song khi qua nó, gọi là thấu kính phân kỳ.
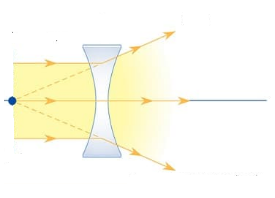
- Mỗi thấu kính có hai tiêu điểm chính F (tiêu điểm vật) và F’ (tiêu điểm ảnh) đối xứng với nhau qua quang tâm.
- Khi đặt vật sáng trước thấu kính thì thu được ảnh của vật, có thể là ảnh thật hoặc ảnh ảo.
3. Mắt
Mắt là một hệ gồm nhiều môi trường trong suốt tiếp giáp nhau bằng các mặt cầu.
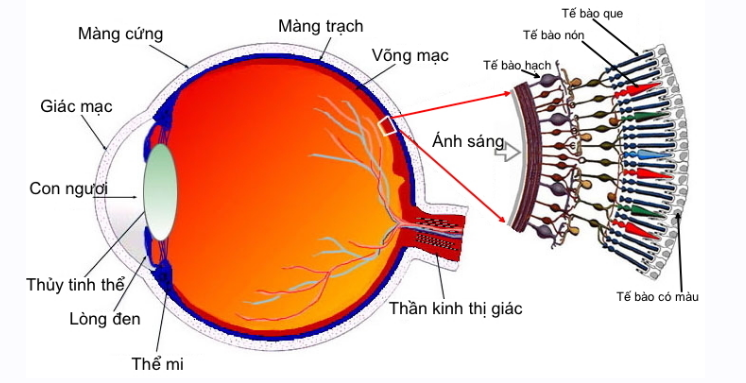
Sự điều tiết của mắt là sự thay đổi tiêu cự của thấu kính mắt (bằng cách thay đổi độ cong của thể thủy tinh) sao cho ảnh của vật cần quan sát hiện rõ nét trên màng lưới.
- Điểm cực cận là điểm gần mắt nhất mà mắt còn nhìn rõ. Càng lớn tuổi, điểm cực cận càng đi ra xa mắt.
- Điểm cực viễn là điểm xa mắt nhất mà mắt còn nhìn rõ. Đối với người có mắt không có tật thì điểm cực viễn ở xa vô cùng.
- Các tật của mắt và cách khắc phục:
|
Tật của mắt |
Đặc điểm |
Cách khắc phục |
|
Mắt cận
Chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm trước màng lưới. |
+ fmax < OV. + OCv hữu hạn. + Không nhìn rỏ các vật ở xa. + Cc ở rất gần mắt hơn bình thường. |
+ Cần đeo thấu kính phân kì + fk = - OCv (kính sát mắt) |
|
Mắt viễn
Chùm tia sáng song song truyền đến mắt cho chùm tia ló hội tụ ở một điểm sau màng lưới. |
+ fmax > OV. + Nhìn vật ở vô cực phải điều tiết. + Cc ở rất xa mắt hơn bình thường. |
+ Cần đeo một thấu kính hội. + Tiêu cự có giá trị sao cho mắt đeo kính nhìn gần như mắt không tật. |
|
Mắt lão
|
Khi tuổi cao khả năng điều tiết giảm vì cơ mắt yếu đi và thể thủy tinh cứng hơn nên điểm cực cận CC dời xa mắt. |
Phải đeo kính hội tụ để nhìn rõ vật ở gần như mắt bình thường.
|
4. Kính lúp
Kính lúp là một dụng cụ quang bổ trợ cho mắt dùng để quan sát các vật nhỏ. Có cấu tạo là một thấu kính hội tụ (hoặc hệ thấu kính ghép tương đương thấu kính hội tụ) có tiêu cự ngắn.
5. Kính hiển vi
Kính hiển vi là một dụng cụ quang bổ trợ cho mắt dùng để quan sát các vật rất nhỏ bằng cách tạo ảnh có góc trông lớn.
Kính hiển vi gồm:
+ Vật kính là một thấu kính hội tụ có tiêu cự rất ngắn (cỡ mm) có tác dụng tạo một ảnh lớn hơn vật.
+ Thị kính là một kính lúp dùng để quan sát ảnh thật tạo bởi vật kính.
Hệ kính được ghép đồng trục sao cho khoảng cách giữa hai kính được giữ không đổi.
Ngoài ra còn có bộ phận tụ sáng để chiếu sáng cho vật cần quan sát (thường là một gương cầu lõm).
6. Kính thiên văn
Kính thiên văn là một dụng cụ quang bổ trợ cho mắt dùng để quan sát các vật ở rất xa bằng cách tăng góc trông.
Kính thiên văn gồm:
+ Vật kính L1 là thấu kính hội tụ có tiêu cự dài (và dm đến vài m) có tác dụng tạo ra một ảnh thật tại tiêu diện của vật kính.
+ Thị kính L2 là thấu kính hội tụ có tiêu cự ngắn (vài cm), có vai trò quan sát ảnh tạo bởi vật kính như một kính lúp.
Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng thay đổi được.
II. Công thức – đơn vị đo
1. Xét một lăng kính có chiết suất n đặt trong không khí.
Công thức lăng kính:
sini1 = n.sin r1
sini2 = n.sin r2
A = r1 + r2
D = i1 + i2 – A
Trong đó:
+ i1 là góc tới của tia sáng từ không khí vào lăng kính tại mặt bên thứ nhất (tại I);
+ i2 là góc ló của tia sáng đi từ lăng kính ra không khí từ mặt bên thứ hai (tại J);
+ D là góc lệch giữa tia tới và tia ló;
+ A là góc ở đỉnh
+ r1 là góc khúc xạ tại mặt bên thứ nhất (tại I)
+ r2 là góc tới của tia sáng tại mặt bên thứ hai (tại J)
2. Công thức thấu kính
Công thức xác định vị trí ảnh: 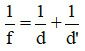
Công thức xác định số phóng đại: 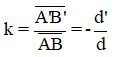
Độ tụ của thấu kính là D = 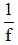
Quy ước về dấu của các đại lượng như sau:
|
Tên đại lượng |
Kí hiệu |
Đơn vị đo |
Quy ước dấu |
|
Tiêu cự |
f |
mét |
Thấu kính hội tụ: f > 0 Thấu kính phân kì: f <0 |
|
Độ tụ |
D |
Diop (dp) |
Thấu kính hội tụ: D > 0 Thấu kính phân kì: D <0 |
|
Khoảng cách từ vật đến TK |
|
mét |
Vật thật: d >0 Vật ảo: d < 0 |
|
Khoảng cách từ ảnh đến TK |
|
mét |
Ảnh thật: d’ >0 Ảnh ảo: d’ <0 |
|
Số phóng đại ảnh |
|
|
Ảnh > vật : |k| >1 Ảnh < vật: |k| <1 Ảnh = vật: |k| = 1 Ảnh cùng chiều vật: k > 0 Ảnh ngược chiều vật: k < 0 |
3. Các công thức về mắt
Độ tụ của mắt được xác định bằng công thức
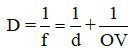
Trong đó:
+ D là độ tụ của mắt, có đơn vị dp;
+ d là khoảng cách từ vật đến mắt, có đơn vị mét (m);
+ OV là khoảng cách từ mắt đến võng mạc, có đơn vị mét (m).
Sửa tật cận thị:
- Mắt cận thị muốn nhìn các vật ở xa vô cùng mà không cần điều tiết cần đeo thấu kính phân kì có tiêu cự là : fk = - (OCV – L)
- Mắt cận thị muốn nhìn các vật ở cách mắt 25 cm như người bình thường cần đeo thấu kính hội tụ có tiêu cự là:
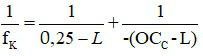
Mắt viễn thị muốn nhìn các vật ở cách mắt 25 cm như người bình thường cần đeo thấu kính hội tụ có tiêu cự là:
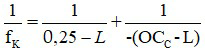
Mắt lão thị cần đeo kính để đọc được sách cách mắt 25 cm như người bình thường tiêu cự kính cần đeo là:
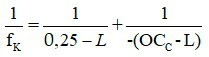
Nếu kính đeo sát mắt thì L = 0
4. Công thức số bội giác của kính lúp
Công thức tổng quát cho các trường hợp: 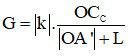
Khi ngắm chừng ở vô cực:
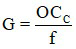
Trong đó:
+ f là tiêu cự của kính lúp, có đơn vị cm hoặc m.
+ OCC là khoảng cực cận của mắt, thường lấy là 25 cm = 0,25 m
+ G là số bội giác khi ngắm chừng ở vô cực.
5. Công thức số bội giác của kính hiển vi
Trường hợp tổng quát: 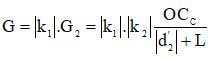
Khi ngắm chừng ở vô cùng
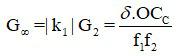
Trong đó:
+ G∞ là số bội giác của kính hiển vi khi ngắm chừng ở vô cực.
+ k1 là số phóng đại ảnh của vật kính L1
+ G2 là số bội giác khi ngắm chừng ở vô cực của thị kính L2
+ δ = F1’F2 = O1O2 – f1 – f2 là độ dài quang học của kính
+ f1 là tiêu cự của vật kính L1
+ f2 là tiêu cực của thị kính L2.
6. Công thức số bội giác của kính thiên văn
Trường hợp tổng quát: 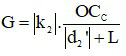
Khi ngắm chừng ở vô cùng:
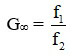
Trong đó :
+ G∞ là số bội giác khi ngắm chừng ở vô cực
+ f1 là tiêu cự của vật kính
+ f2 là tiêu cự của thị kính
+ L là khoảng cách giữa hai kính.
III. Mở rộng
1. Nếu góc chiết quang A nhỏ (< 100), ta gọi lăng kính là nêm quang học.
Chiếu tới nêm quang học một tia tới có góc tới i nhỏ (i<100), ta có các công thức lăng kính như sau:
i1 = nr1 ; i2 = nr2
A = r1 + r2
D = (n-1).A
2. Đối với hệ thấu kính đồng trục L1, L2 có khoảng cách giữa hai tâm là O1O2 thì ảnh của L1 trở thành vật đối với thấu kính L2
Khi đó khoảng cách từ vật sáng A1’B1’ đến thấu kính L2 là: d2 = O1O2 - d1’
Số phóng đại ảnh k = k1k2 = 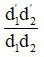
Trong đó:
+ d2 là khoảng cách từ ảnh của vật AB tạo bởi thấu kính L1, nay là vật sáng đối với L2 đến thấu kính L2.
+ d1’ là khoảng cách từ ảnh của vật AB tạo bởi thấu kính L1 đến thấu kính L1
+ O1O2 là khoảng cách giữa hai quang tâm của hai thấu kính.
Nếu hệ thấu kính ghép sát thì O1O2 = 0, khi đó d2 = -d1’ và k = k1k2 = 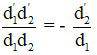
Độ tụ của thấu kính tương đương với hệ hai thấu kính mỏng đồng trục ghép sát là:
D = D1 + D2
Trong đó:
+ D là độ tụ thấu kính tương đương, có đơn vị dp;
+ D1 và D2 lần lượt là độ tụ của các thấu kính trong hệ ghép sát đồng trục, có đơn vị dp.
IV. Bài tập ví dụ
Bài 1: Một lăng kính thủy tinh có chiết suất n = 1,5 . Tiết diện thẳng là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới 300. Xác định đường truyền của tia sáng.
Bài giải:
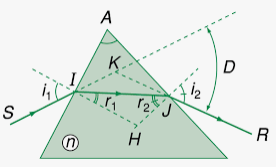
Tại I luôn có tia khúc xạ, ta có:
Sini1 = nsinr1
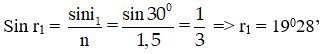
Tại J: r2 = 600 – 19028’ = 40032’
Áp dụng công thức thấu kính, ta có: Sini2 = nsinr2 ⇒ i2 = 770
Bài 2: Cho một thấu kính hội tụ có tiêu cự f = 20 cm. Đặt một vật sáng AB cao 4 cm trước thấu kính và cách thấu kính 40 cm. Xác định vị trí và chiều cao của ảnh.
Bài giải:
Áp dụng công thức thấu kính:
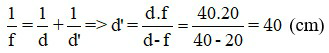
Áp dụng công thức độ phóng đại ảnh
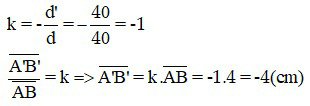
Vậy ảnh A’B’ cao 4 cm, dấu “-” cho biết ảnh ngược chiều với vật.
Bài 3:
Một kính hiển vi có các tiêu cự vật kính và thị kính là f1 = 1 cm và f2 = 4 cm. Độ dài quang học của kính là 20 cm. Người quan sát có mắt không bị tật và có khoảng cực cận là OCC = 20 cm. Tính số bội giác khi ngắm chừng ở vô cực.
Bài giải:
Áp dụng công thức 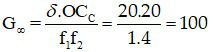
Đáp án: G∞ = 100.
....................................
....................................
....................................
Trên đây là phần tóm tắt một số công thức Vật Lí lớp 11 Chương 7: Mắt. Các dụng cụ quang năm học 2021 - 2022 quan trọng, để xem chi tiết mời quí bạn đọc vào từng công thức trên!
Xem thêm các bài tổng hợp Công thức Vật Lí lớp 11 đầy đủ, chi tiết khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

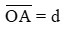
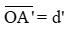
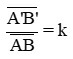
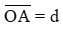
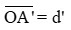
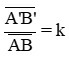



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

