Tổng hợp lý thuyết Toán 11 Chương 6 Chân trời sáng tạo
Tổng hợp lý thuyết Toán 11 Chương 6: Hàm số mũ và hàm số lôgarit sách Chân trời sáng tạo hay nhất, chi tiết với bài tập có lời giải sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm Toán 11 Chương 6.
Tổng hợp lý thuyết Toán 11 Chương 6 Chân trời sáng tạo
(199k) Xem Khóa học Toán 11 CTST
Lý thuyết tổng hợp Toán 11 Chương 6
1. Lũy thừa với số mũ nguyên
Ở cấp Trung học cơ sở, chúng ta đã biết lũy thừa với số mũ tự nhiên:
Phép tính lũy thừa có thể mở rộng với số mũ nguyên bất kì. Lũy thừa với số mũ nguyên âm được định nghĩa như sau:
Với số nguyên dương n, số thực , lũy thừa của a với số mũ –n xác định bởi
Chú ý:
a) a0 = 1 với mọi a ∈ ℝ, a ≠ 0.
b) 00 và 0–n (với n > 0) không có nghĩa.
2. Căn bậc n
Mở rộng phép lấy căn bậc hai, căn bậc ba đã quen thuộc ở cấp Trung học cơ sờ, ta có định nghĩa sau đây:
Cho số nguyên dương và số thực b bất kì. Nếu có số thực a sao cho
thì a được gọi là một căn bậc n của b.
Chú ý: Ở cấp Trung học cơ sở ta đã biết:
a) Nếu b > 0 thì b có hai căn bậc hai, kí hiệu là (gọi là căn bậc hai số học của b) và ;
b) Số 0 chỉ có duy nhất một căn bậc hai là chính nó;
c) Nếu b < 0 thì b không có căn bậc hai nào;
d) Mọi số thực b có duy nhất một căn bậc ba, kí hiệu là .
Mở rộng kết quả này, ta có:
Cho n là số nguyên dương là số thực bất kì. Khi đó:
+ Nếu n là số chẵn thì:
• b < 0: không tồn tại căn bậc n của b.
• b = 0: có một căn bậc n của b là 0.
• b > 0: có hai căn bậc n của b đối nhau, kí hiệu giá trị dương là và giá trị âm là .
+ Nếu n là số lẻ thì có duy nhất một căn bậc n của b, kí hiệu .
Chú ý:
a) Nếu n chẵn thì căn thức có nghĩa chi khi .
b) Nếu n lẻ thì căn thức luôn có nghĩa với mọi số thực b.
Tính chất của căn bậc n
Ta có các tính chất sau đây (với điều kiện các căn thức đều có nghĩa):
•
•
•
•
•
3. Lũy thừa với số mũ hữu tỉ
Cho số thực dương a và số hữu tỉ , trong đó .
Luỹ thừa của a với số mũ r, kí hiệu ar, được xác định bởi
4. Lũy thừa với mũ thực
Môt cách tổng quát, với alà số thực dương, α là số vô tỷ bất kỳ, người ta chứng minh được rằng có dãy số hữu tỉ sao cho và dãy số có giới hạn không phụ thuộc vào việc chọn dãy .
Giới hạn của dãy số được gọi là lũy thừa của số thực dương a với số mũ α, kí hiệu là .
với .
Chú ý: với mọi .
5. Tính chất của phép tính lũy thừa
Phép tính luỹ thừa với số mũ thực có tính chất tương tự như luỹ thừa với số mũ tự nhiên.
Cho a, b là những số thực dương; α, β là những số thực bất kì. Khi đó:
6. Khái niệm lôgarit
Cho hai số thực dương a, b với . Số thực α thoả mãn đẳng thức được gọi là lôgarit cơ số a của b và kí hiệu là .
.
Chú ý:
a) Biểu thức chỉ có nghĩa khi và b > 0.
b) Từ định nghĩa lôgarit, ta có:
Hai công thức (3) và (4) cho thấy phép lấy lôgarit và phép nâng lên luỹ thừa là hai phép toán ngược nhau.
7. Tính lôgarit bằng máy tính cầm tay
Sử dụng máy tính cầm tay, ta có thể tính nhanh giá trị của các lôgarit (thường cần lấy giá trị gần đúng bằng cách làm tròn đến hàng nào đó).
Chú ý:
a) Lôgarit cơ số 10 được gọi là lôgarit thập phân. Ta viết log N hoặc lg N thay cho .
b) Lôgarit cơ số e còn được gọi là lôgarit tự nhiên. Ta viết ln N thay cho .
8. Tính chất của phép tính lôgarit
Cho các số thực dương a, M, N với , ta có:
•
•
•
Chú ý: Đặc biệt, a, M, N với dương,, ta có:
9. Công thức đổi cơ số của lôgarit
Cho các số dương , ta có
Đặc biệt, ta có:
10. Hàm số mũ
Cho số thực dương a khác 1.
Hàm số cho tương ứng mỗi số thực x với số thực được gọi là hàm số mũ cơ số a, kí hiệu .
Nhận xét: Hàm số có tập xác định là .
Đồ thị của hàm số mũ
Tổng quát, ta có đồ thị của hàm số với a > 1 và 0 < a < 1 như sau:
Từ đó, hàm số có:
(1) Tập xác định: .
Tập giá trị: .
Hàm số liên tục trên .
(2) Sự biến thiên:
• Nếu a > 1 thì hàm số đồng biến trên và
• Nếu 0 < a < 1 thì hàm số nghịch biến trên và
(3) Đồ thị:
• Cắt trục tung tại điểm (0; 1); đi qua điểm (1; a).
• Nằm phía trên trục hoành.
11. Hàm số lôgarit
Cho số thực dương a khác 1.
Hàm số cho tương ứng với mỗi số thực dương x với số thực được gọi là hàm số lôgarit cơ số a, kí hiệu là .
Nhận xét: Hàm số có tập xác định là .
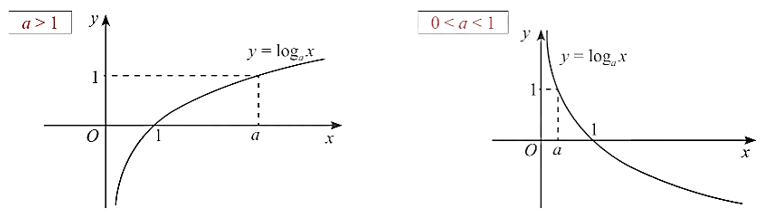
Đồ thị của hàm số lôgarit
Tổng quát, ta có đồ thị hàm số với a > 1 và 0 < a < 1 như sau:
Từ đó, hàm số có:
(1) Tập xác định: .
Tập giá trị: .
Hàm số liên tục trên .
(2) Sự biến thiên:
• Nếu a > 1 thì hàm số đồng biến trên và
• Nếu 0 < a < 1 thì hàm số nghịch biến trên và
(3) Đồ thị
• Cắt trục hoành tại điểm (1; 0), đi qua điểm (a; 1).
• Nằm bên phải trục tung.
12. Phương trình mũ
Phương trình dạng , trong đó a và b là những số cho trước, , được gọi là phương trình mũ cơ bản.
Nghiệm của phương trình mũ cơ bản
Cho phương trình .
Nếu b > 0 thì phương trình luôn có nghiệm duy nhất .
Nếu b ≤ 0 thì phương trình vô nghiệm.
Chú ý:
a) Nếu thì ta có .
b) Tổng quát hơn, .
13. Phương trình lôgarit
Phương trình dạng , trong đó a, b là những số cho trước, a > 0, , được gọi là phương trình lôgarit cơ bản.
Nghiệm của phương trình lôgarit cơ bản
Phương trình luôn có nghiệm duy nhất .
Chú ý: Tổng quát, xét phương trình dạng
. (1)
Để giải phương trình (1), trước hết cần đặt điều kiện có nghĩa: và .
Khi đó, (1) được biến đổi thành phương trình
. (2)
Sau khi giải phương trình (2), ta cần kiểm tra sự thỏa mãn điều kiện. Nghiệm của phương trình (1) là nghiệm của (2) thỏa mãn điều kiện.
14. Bất phương trình mũ
Bất phương trình mũ cơ bản là bất phương trình có dạng (hoặc , ,), với a, b là những số cho trước, a > 0, .
Xét bất phương trình
. (3)
Nghiệm của (3) là hoành độ các điểm trên đồ thị hàm số nằm phía trên đường thẳng y = b. Từ đồ thị ở hình dưới đây,
ta nhận được:
• Nếu b ≤ 0 thì mọi đều là nghiệm của (3).
• Nếu b > 0 thì:
+ Với a > 1, nghiệm của (3) là ;
+ Với 0 < a < 1, nghiệm của (3) là .
Chú ý:
a) Tương tự như trên, từ đồ thị ở hình trên, ta nhận được kết quả về nghiệm của mỗi bất phương trình (các bất phương trình vô nghiệm nếu ).
b) Nếu a > 1 thì .
Nếu 0 < a < 1 thì .
15. Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản là bất phương trình có dạng (hoặc ), với a, b là các số cho trước, .
Xét bất phương trình
(4).
Điều kiện xác định của bất phương trình là x > 0.
Nghiệm của (4) là hoành độ các điểm của đồ thị hàm số nằm phía trên đường thẳng . Từ đồ thị ở hình dưới đây,
ta nhận được:
• Với a > 1, nghiệm của (4) là .
• Với 0 < a < 1, nghiệm của (4) là .
Chú ý:
a) Tương tự như trên, từ đồ thị ở hình trên, ta nhận được kết quả về nghiệm của mỗi bất phương trình .
b) Nếu a > 1 thì .
Nếu 0 < a < 1 thì .
Bài tập tổng hợp Toán 11 Chương 6
Bài 1. Thực hiện phép tính:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
a) ;
b)
;
c)
d) .
Bài 2. Viết các biểu thức sau dưới dạng một lũy thừa:
a) ;
b) (a ≥ 0);
c) (b > 0).
Hướng dẫn giải
a) ;
b) Với a ≥ 0, ta có
;
c) Với b > 0, ta có .
Bài 3. Rút gọn các biểu thức sau:
a) (x > 0);
b) (a > 0);
c) (x ≥ 0);
d) (a, b > 0).
Hướng dẫn giải
a) ;
b) ;
c) ;
d) .
Bài 4. Ông An gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,8%/ tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào gốc để tính lãi cho tháng tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi thêm vào tài khoản với số tiền 2 triệu đồng. Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu? Biết rằng trong suốt thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra.
Hướng dẫn giải
Với 100 triệu đồng ban đầu số tiền cả lãi và gốc thu được sau hai năm là
(đồng).
Mỗi tháng tiếp theo gửi 2 triệu đồng thì tổng số tiền cả lãi và gốc là
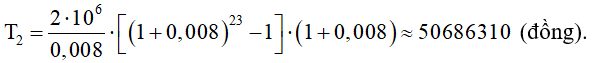
Vậy tổng số tiền ông An nhận được là (đồng).
Bài 5. Tính:
a)
b) ;
c)
d)
Hướng dẫn giải
a) .
b) .
c) .
d) .
Bài 6. Tính giá trị của các biểu thức sau:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
a)
b) .
c) Ta có ;
Vậy .
d)
.
Bài 7. Rút gọn các biểu thức sau:
a) (a, b > 0; a ≠ 1);
b) (a, b, c, d > 0);
c) (x > 0);
d) ().
Hướng dẫn giải
a) .
b) .
c)
d) 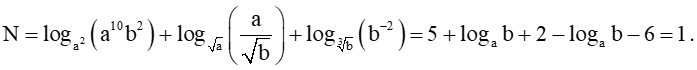
Bài 8.
a) Cho các số thực dương a, b thỏa mãn , . Tính .
b) Đặt . Biểu diễn theo a và b.
Hướng dẫn giải
a)
b) Ta có
.
Bài 9. Để tính độ tuổi của mẫu vật bằng gỗ, người ta đo độ phóng xạ của có trong mẫu vật tại thời điểm t (năm) (so với thời điểm ban đầu t = 0), sau đó sử dụng công thức tính độ phóng xạ (đơn vị là Becquerel, kí hiệu Bq) với H0 là độ phóng xạ ban đầu (tại thời điểm t = 0); là hằng số phóng xạ, T = 5730 (năm) (Nguồn: Vật lí 12 Nâng cao, NXBGD Việt Nam, 2014). Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ là 0,215 Bq. Biết độ phóng xạ của mẫu gỗ tươi cùng loại là 0,250 Bq. Xác định độ tuổi của mẫu gỗ cổ đó (làm tròn kết quả đến hàng đơn vị).
Hướng dẫn giải
Gọi t là độ tuổi của mẫu gỗ cổ.
Ta có: với .
Từ đó, . Vậy .
Vậy độ tuổi của mẫu gỗ cổ đó xấp xỉ 1247 năm.
Bài 10. Vẽ đồ thị hàm số .
Hướng dẫn giải
Tập xác định: .
Do nên hàm số đồng biến trên .
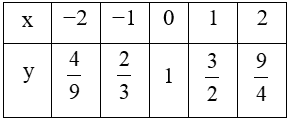
Bảng giá trị:
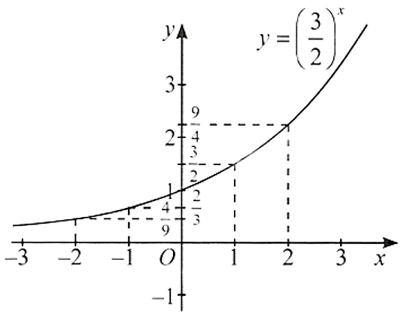
Đồ thị hàm số đi qua các điểm có toạ độ theo bảng giá trị và nằm phía trên trục hoành.
Từ đó, ta vẽ được đồ thị hàm số như hình dưới đây.
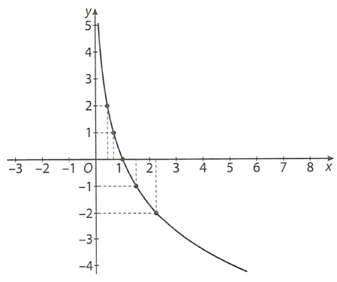
Bài 11. Vẽ đồ thị của hàm số .
Hướng dẫn giải
Lập bảng giá trị của hàm số tại một số điểm như sau:
Từ đó, ta vẽ được đồ thị của hàm số như hình sau:
Bài 12. Tìm tập xác định của các hàm số sau:
a) ;
b) .
Hướng dẫn giải
a) Tập xác định của hàm số là .
b) Hàm số xác định khi hay .
Vậy tập xác định của hàm số là .
Bài 13. So sánh các cặp số sau:
a) 2,50,3 và 2,50,5;
b) và .
Hướng dẫn giải
a) Do 2,5 > 1 nên hàm số y = 2,5x đồng biến trên ℝ. Mà 0,3 < 0,5 nên 2,50,3 < 2,50,5.
b) Hàm số có cơ số 0,7 < 1 nên nghịch biến trên (0; +∞).
Mà 4 < 4,1 nên > .
Bài 14. Sau khi bệnh nhân uống một liều thuốc, lượng thuốc còn lại trong cơ thể giảm dần và được tính theo công thức , trong đó D0 và a là các hằng số dương, t là thời gian tính bằng giờ kể từ thời điểm uống thuốc.
a) Tại sao có thể khẳng định rằng 0 < a < 1?
b) Biết rằng bệnh nhân đã uống 100 mg thuốc và sau 1 giờ thì lượng thuốc trong cơ thể còn 80 mg. Hãy xác định giá trị của D0 và a.
c) Sau 5 giờ, lượng thuốc đã giảm đi bao nhiêu phần trăm so với lượng thuốc ban đầu?
Hướng dẫn giải
a) Do lượng thuốc trong cơ thể giảm dần, nên hàm số D(t) nghịch biến, mà D0 là hằng số dương, do đó 0 < a < 1.
b) Bệnh nhân đã uống 100 mg thuốc nên D0 = 100.
Vì sau 1 giờ thì lượng thuốc trong cơ thể còn 80 mg nên với t = 1, ta có:
D(1) = 100a1 = 80, suy ra .
c) Sau 5 giờ, lượng thuốc còn . Tỉ lệ lượng thuốc đã giảm so với lượng thuốc ban đầu là.
Bài 15. Giải các phương trình sau:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
a) Ta có:
Vậy phương trình có nghiệm duy nhất là .
b) Ta có:
Vậy phương trình có nghiệm duy nhất là .
c) Điều kiện: x > 1.
Khi đó: .
Giải phương trình trên ta được x = – 1 (không thỏa mãn) và x = 4 (thỏa mãn điều kiện).
Vậy phương trình đã cho có nghiệm là x = 4.
d) .
Vậy phương trình đã cho có nghiệm là x = –1.
Bài 16. Giải các phương trình sau:
a) ;
b) .
Hướng dẫn giải
a) Ta có:
Vậy nghiệm của phương trình đã cho là .
b) Điều kiện: x + 6 > 0 và x + 2 > 0, tức là x > –2. Ta có:
Giải phương trình bậc hai này ta được hai nghiệm . Chỉ có nghiệm thoả mãn điều kiện.
Vậy nghiệm của phương trình đã cho là .
Bài 17. Giải các bất phương trình sau:
a) ;
b) ;
c)
d) ;
e)
g) .
Hướng dẫn giải
a) .
Vậy tập nghiệm của bất phương trình là
b)
c)
Bất phương trình đã cho có thể viết ở dạng: .
Vì cơ số 3 > 1 nên bất phương trình trở thành , hay .
Giải bất phương trình này, ta được .
Vậy tập nghiệm của bất phương trình đã cho là .
d)
Vậy tập nghiệm của bất phương trình là
e) .
Điều kiện: x > 3.
Khi đó, bất phương trình đã cho được viết lại thành
Vì cơ số 0,5 < 1 nên bất phương trình trở thành (x – 3)(x – 2) ≤ 2, hay .
Giải bất phương trình bậc hai này, ta được 1 ≤ x ≤ 4.
Kết hợp với điều kiện, ta được nghiệm của bất phương trình là 3 < x ≤ 4.
g) Điều kiện: . Ta có
Kết hợp với điều kiện, ta được: .
Bài 18. Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất là 6%/ năm. Để có được số tiền cả gốc và lãi nhiều hơn 130 triệu đồng thì người đó phải gửi ít nhất bao nhiêu năm? Biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.
Hướng dẫn giải
Gọi x là số năm người đó gửi tiền trong ngân hàng.
Số tiền cả gốc và lãi người đó có được sau x năm được tính bởi công thức:
Để có được số tiền cả gốc và lãi nhiều hơn 130 triệu đồng thì
Do kì hạn gửi là 12 tháng nên để rút được số tiền cả gốc và lãi nhiều hơn 130 triệu đồng thì người đó phải gửi ít nhất 5 năm.
Học tốt Toán 11 Chương 6
Các bài học để học tốt Tổng hợp lý thuyết Toán 11 Chương 6 Toán lớp 11 hay khác:
(199k) Xem Khóa học Toán 11 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 11 Chân trời sáng tạo hay khác:
Lý thuyết Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit
Lý thuyết Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Xem thêm các tài liệu học tốt lớp 11 hay khác:
- Giải sgk Toán 11 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải SBT Toán 11 Chân trời sáng tạo
- Giải lớp 11 Chân trời sáng tạo (các môn học)
- Giải lớp 11 Kết nối tri thức (các môn học)
- Giải lớp 11 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST

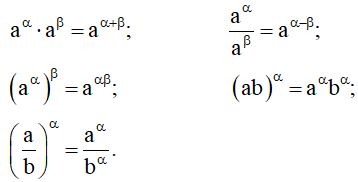

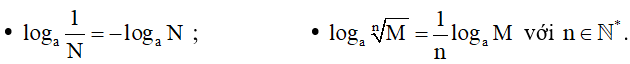

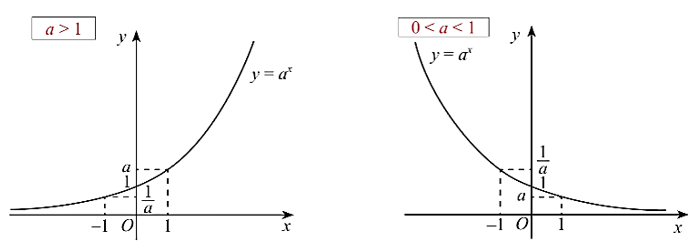
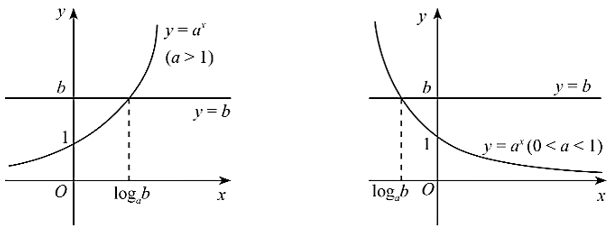
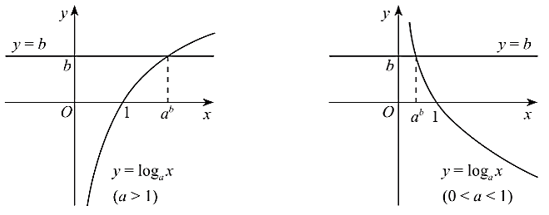
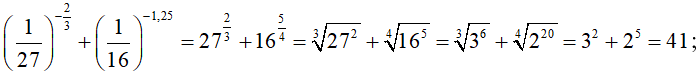
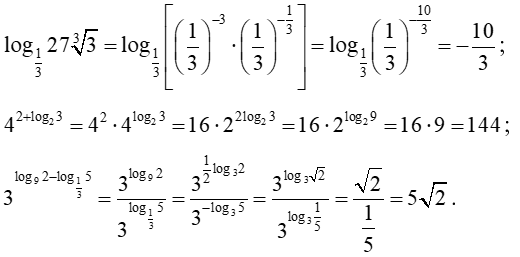
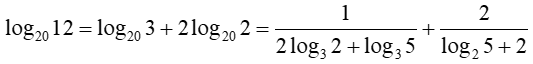

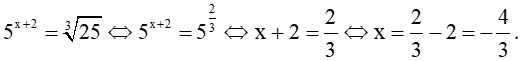
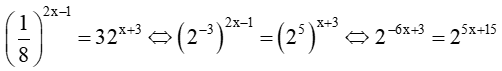
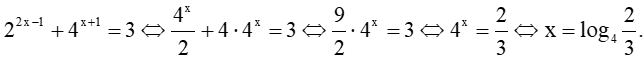
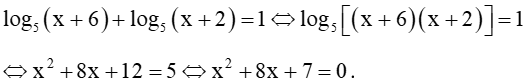
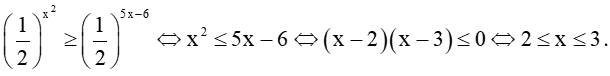
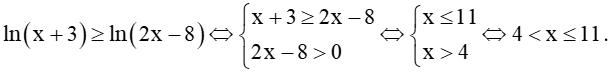
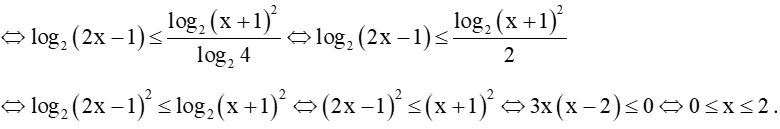



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

