Tổng hợp lý thuyết Toán 8 Chương 9 Chân trời sáng tạo
Tổng hợp lý thuyết Toán 8 Chương 9: Tổng hợp lý thuyết Toán 8 Chương 9 sách Chân trời sáng tạo hay nhất, chi tiết cùng các bài tập có lời giải sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm Toán 8 Chương 9.
Tổng hợp lý thuyết Toán 8 Chương 9 Chân trời sáng tạo
(199k) Xem Khóa học Toán 8 CTST
Bài giảng: Bài tập cuối chương 9 - Cô Vương Hạnh (Giáo viên VietJack)
Lý thuyết tổng hợp Toán 8 Chương 9
1. Kết quả thuận lợi
Trong một phép thử, mỗi kết quả làm cho một biến cố xảy ra được gọi là một kết quả thuận lợi cho biến cố đó.
2. Mô tả xác suất bằng tỉ số
Khi tất cả các kết quả của một trò chơi hay phép thử nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra của biến cố A là tỉ số giữa kết quả thuận lợi cho A và tổng kết quả có thể xảy ra của phép thử, tức là
Để phân biệt với xác suất thực nghiệm thực nghiệm, xác suất P(A) xác định ở công thức trên còn được gọi là xác suất lí thuyết của biến cố A.
Chú ý: A và B là hai biến cố khác nhau nhưng có xác suất xảy ra bằng nhau. Ta nói A và B là hai biến cố đồng khả năng.
3. Xác suất lí thuyết và xác suất thực nghiệm
Gọi P(A) là xác suất thực xuất hiện của biến cố A khi thực hiện một phép thử.
Gọi m(A) là số lần xuất hiện biến cố A khi thực hiện phép thử đó m lần.
Xác suất thực nghiệm của biến cố A là tỉ số
Khi m càng lớn, xác suất thực nghiệm của biến cố A càng gần P(A).
Nhận xét:
• Xác suất thực nghiệm phụ thuộc vào kết quả của dãy phép thử và chỉ được xác định sau khi đã thực hiện dãy phép thử.
• Xác suất lí thuyết có thể được xác định trước khi thực hiện phép thử.
• Xác suất thực nghiệm và xác suất lí thuyết của cùng một sự kiện hay biến cố không nhất thiết là bằng nhau. Tuy nhiên, khi thực hiện càng nhiều lần phép thử, xác suất thực nghiệm càng gần xác suất lí thuyết.
Nhận xét:
• Xác suất thực nghiệm của biến cố A có thể lớn hơn hoặc nhỏ hơn xác suất lí thuyết.
• Khi số lần thực hiện phép thử lớn thì xác suất thực nghiệm của biến cố A gần bằng xác suất lí thuyết.
Bài tập tổng hợp Toán 8 Chương 9
Bài 1. Trong tủ quần áo của bạn Hải có 3 chiếc áo sơ mi trơn màu trắng, 2 chiếc áo sơ mi kẻ sọc và 2 chiếc áo sơ mi trơn màu xanh, tất cả các áo đều khác nhau. Hải chọn ngẫu nhiên một chiếc áo trong tủ để mặc. Hỏi có bao nhiêu kết quả thuận lợi cho biến cố “Chiếc áo được chọn không phải áo kẻ sọc”?
Hướng dẫn giải
Trong các kết quả có thể của hành động, các kết quả để biến cố “Chiếc áo được chọn không phải áo kẻ sọc” xảy ra là 3 chiếc áo sơ mi trơn màu trắng, 2 chiếc áo sơ mi trơn màu xanh.
Do đó, có 5 kết quả thuận lợi cho biến cố.
Bài 2.Bạn Mai thực nghiệm gieo một con xúc xắc 6 mặt. Liệt kê các kết quả thuận lợi của biến cố “Số chấm xuất hiện trên con xúc xắc là số nguyên tố”.
Hướng dẫn giải
Trong các kết quả có thể là {1; 2; 3; 4; 5; 6} của thực nghiệm, các kết quả để biến cố “Số chấm xuất hiện trên con xúc xắc là số nguyên tố” xảy ra là {2; 3; 5}.
Vậy có 3 kết quả thuận lợi cho biến cố đã cho là {2; 3; 5}.
Bài 3. Lớp 8A có 30 học sinh, trong đó có 12 nữ. Trong lớp có 2 học sinh nữ cận thị và 6 học sinh nam không cận thị. Chọn ngẫu nhiên một học sinh trong lớp. Tính số kết quả thuận lợi cho biến cố “Chọn được học sinh nữ không cận thị” và biến cố “Chọn được học sinh cận thị”?
Hướng dẫn giải
Số học sinh nữ không cận thị là: 12 – 2 = 10 (học sinh).
Do đó, có 10 kết quả thuận lợi cho biến cố “Chọn được học sinh nữ không cận thị”.
Số học sinh nam lớp 8A có 30 – 12 = 18 (học sinh).
Số học sinh nam cận thị là: 18 – 6 = 12 (học sinh).
Số học sinh cận thị lớp 8A là: 12 + 2 = 14 (học sinh).
Do đó, có 14 kết quả thuận lợi cho biến cố “Chọn được học sinh cận thị”.
Vậy có 10 kết quả thuận lợi cho biến cố “Chọn được học sinh nữ không cận thị” và 14 kết quả thuận lợi cho biến cố “Chọn được học sinh cận thị”.
Bài 4. Một túi đựng 20 viên bi giống hệt nhau nhưng khác màu, trong đó có 7 bi trắng, 4 bi vàng, 6 bi đen và 3 bi xanh. Bạn Kỳ lấy ngẫu nhiên một viên bi từ túi. Tính xác suất để Kỳ lấy được viên bi trắng.
Hướng dẫn giải
Số kết quả có thể là 20.
Bạn Kỳ lấy ngẫu nhiên nên các kết quả có thể là đồng khả năng.
Gọi E là biến cố “Kỳ lấy được viên bi trắng”. Có 7 kết quả thuận lợi cho E.
Vậy .
Bài 5. Một hộp đựng các tấm thẻ được ghi số 10; 11; 12; …; 20. Rút ngẫu nhiên một tấm thẻ từ hộp. Tính xác suất để rút được tấm thẻ ghi số là số nguyên tố.
Hướng dẫn giải
Số kết quả có thể là 11.
Chọn ngẫu nhiên một thẻ nên các kết quả có thể là đồng khả năng.
Có 4 tấm thẻ ghi số nguyên tố là 11; 13; 17; 19. Do đó, có 4 kết quả thuận lợi.
Vậy xác suất để rút được tấm thẻ ghi số là số nguyên tố là .
Bài 6. Bạn Mai có các tấm thẻ, mỗi tấm thẻ ghi một chữ cái trong từ “TOANHOC”. Bạn Mai rút ngẫu nhiên một tấm thẻ. Tính xác suất để rút được tấm thẻ ghi chữ A hoặc chữ O.
Hướng dẫn giải:
Có 7 chữ cái trong từ “TOANHOC” nên số kết quả có thể là 7.
Chọn ngẫu nhiên một thẻ nên các kết quả có thể là đồng khả năng.
Có 3 tấm thẻ ghi chữ A hoặc O nên có 3 kết quả thuận lợi.
Xác suất để rút được tấm thẻ ghi chữ T là .
Bài 7. Trong túi đựng 9 đôi tất, gồm 6 đôi tất màu trắng và còn lại là màu đen. Lấy ngẫu nhiên một đôi tất từ túi. Tính xác suất chọn được đôi tất màu đen.
Hướng dẫn giải
Số kết quả có thể là 9.
Chọn ngẫu nhiên một đôi tất nên các kết quả có thể là đồng khả năng.
Số đôi tất màu đen là 9 – 6 = 3 (đôi). Do đó, có 3 kết quả thuận lợi cho biến cố.
Vậy xác suất chọn được đôi tất màu đen là .
Bài 8. Vy gieo ba con xúc xắc 6 mặt cân đối và đồng chất. Tính xác suất của biến cố “Tích số chấm xuất hiện trên ba con xúc xắc là 28”.
Hướng dẫn giải:
Ta có 28 = 22 . 7 = 2 . 2 . 7 = 1 . 4 . 7 = 1 . 2 . 14.
Vì con xúc xắc có số chấm trên mỗi mặt là từ 1 đến 6 nên tích số chấm xuất hiện trên ba con xúc xắc là 28 không thể xảy ra.
Do đó không có kết quả thuận lợi cho biến cố “Tích số chấm xuất hiện trên ba con xúc xắc là 28”.
Vậy xác suất là 0.
Bài 9. Một túi đựng 24 viên kẹo có cùng khối lượng và kích thước, trong đó có một số viên vị dâu, một số viên vị táo, còn lại là vị sữa. Lấy ngẫu nhiên một viên kẹo từ trong túi. Biết rằng xác suất lấy được viên vị dâu và vị táo tương ứng là và . Tính số viên kẹo vị sữa trong túi.
Hướng dẫn giải
Gọi x, y lần lượt là số viên kẹo vị dâu, vị táo trong túi.
Xác suất lấy được viên vị dâu và vị táo lần lượt là và .
Theo đề bài ta có
• nên x = 8;
• nên y = 4.
Do đó, số viên kẹo vị sữa trong túi là 24 – 8 – 4 = 12 (viên).
Vậy số viên kẹo vị sữa trong túi là 12 viên.
Bài 10. Thống kê điểm kiểm tra giữa kì 1 môn Toán của một nhóm 100 học sinh lớp 8 được chọn ngẫu nhiên tại trường X, thu được kết quả như sau:
|
Số điểm |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
6 |
10 |
11 |
11 |
11 |
13 |
13 |
9 |
8 |
8 |
Chọn ngẫu nhiên một học sinh trường X được khảo sát. Tính xác suất thực nghiệm của biến cố “Học sinh đó có điểm lớn hơn hoặc bằng 5”.
Hướng dẫn giải
Trong 100 học sinh được khảo sát, số học sinh có điểm lớn hơn hoặc bằng 5 là:
11 + 13 + 13 + 9 + 8 + 8 = 62 (học sinh).
Xác suất thực nghiệm của biến cố “Học sinh đó có điểm lớn hơn hoặc bằng 5” là:
.
Vậy xác suất thực nghiệm của biến cố “Học sinh đó có điểm lớn hơn hoặc bằng 5” là .
Bài 11. Khảo sát chiều cao của 80 em học sinh lớp 8 trường X, thu được kết quả như sau:
|
Chiều cao (cm) |
< 120 |
120 – 140 |
141 – 160 |
> 160 |
|
Số lượng (học sinh) |
4 |
22 |
39 |
15 |
Chọn ngẫu nhiên một học sinh được khảo sát. Tính xác suất của biến cố “học sinh đó có chiều cao từ 141 cm trở lên.
Hướng dẫn giải
Trong 80 học sinh được khảo sát, số học sinh có chiều cao từ 141 cm trở lên là:
39 + 15 = 54 (học sinh).
Xác suất của biến cố “học sinh đó có chiều cao từ 141 cm trở lên” là .
Bài 12. Khảo sát thể loại phim yêu thích nhất của 100 học sinh trường A, thu được kết quả như bảng sau:
|
Thể loại |
Hành động |
Lãng mạn |
Khoa học viễn tưởng |
Tài liệu |
Hoạt hình |
Khác |
|
Số học sinh |
38 |
15 |
19 |
5 |
17 |
6 |
Chọn ngẫu nhiên một học sinh trường A được khảo sát. Tính xác suất thực nghiệm của biến cố “Học sinh đó yêu thích thể loại phim tài liệu hoặc khoa học viễn tưởng nhất”.
Hướng dẫn giải
Trong 100 học sinh được khảo sát, có 19 + 5 = 24 học sinh yêu thích thể loại phim tài liệu hoặc khoa học viễn tưởng nhất.
Xác suất thực nghiệm của biến cố “Học sinh đó yêu thích thể loại phim tài liệu nhất” là .
Bài 13. Thống kê về số ca nhiễm bệnh và số ca tử vong của bệnh SARS từ tháng 11-2002 đến tháng 7-2003 được kết quả như sau: 8 437 người nhiễm, trong đó có 813 người tử vong. Tính xác suất một người tử vong khi nhiễm bệnh SARS.
Hướng dẫn giải
Thống kê 8 437 người nhiễm, trong đó có 813 người tử vong.
Xác suất thực nghiệm của biến cố trên là .
Vậy xác suất một người tử vong khi nhiễm bệnh SARS khoảng 9,6%.
Bài 14.Một trang web tiến hành khảo sát trực tuyến ý kiến của khán giả về một bộ phim mới ra rạp và kết quả cho thấy trong 98 người tham gia khảo sát, có 62 người thích bộ phim, 25 người không thích bộ phim và còn lại không có ý kiến. Hỏi trong 500 người thì có khoảng bao nhiêu người thích bộ phim đó?
Hướng dẫn giải
Trong 98 người tham gia khảo sát, có 62 người thích bộ phim.
Xác suất người đó thích bộ phim được ước lượng là .
Gọi k là số người thích bộ phim trong 500 người.
Ta có nên .
Vậy có khoảng 316 người thích bộ phim trong 500 người.
Bài 15.Một nhà máy sản xuất tủ lạnh tiến hành kiểm tra chất lượng của 500 chiếc tủ lạnh được sản xuất và thấy có 3 chiếc bị lỗi. Trong một lô hàng có 1 000 chiếc tủ lạnh. Hãy dự đoán xem có khoảng bao nhiêu chiếc tủ lạnh không bị lỗi.
Hướng dẫn giải
Trong 500 chiếc được kiểm tra, số chiếc không bị lỗi là: 500 – 3 = 497 (chiếc).
Xác suất để một chiếc tủ lạnh do nhà máy sản xuất không bị lỗi ước lượng là .
Gọi k là số tủ lạnh không bị lỗi trong 1 000 chiếc tủ lạnh.
Ta có nên .
Vậy có khoảng 994 chiếc tủ lạnh không bị lỗi trong 1 000 chiếc.
Bài 16. Một cửa hàng điện thoại thống kê lại số lượng các hãng điện thoại bán trong năm qua như sau:
|
Hãng |
Apple |
Samsung |
Oppo |
Redmi |
Realme |
Khác |
|
Số lượng (chiếc) |
66 |
85 |
51 |
94 |
89 |
28 |
Giả sử năm sau cửa hàng bán được tổng 500 chiếc các hãng. Hãy dự đoán xem trong đó có khoảng bao nhiêu chiếc Oppo.
Hướng dẫn giải:
Tổng số điện thoại các hãng bán được trong năm qua là:
66 + 85 + 51 + 94 + 89 + 28 = 413 (chiếc).
Trong đó có 51 chiếc Oppo.
Xác suất chiếc điện thoại bán được là Oppo được ước lượng là .
Gọi k là số chiếc Oppo bán được trong năm sau.
Ta có nên .
Vậy dự đoán có khoảng 62 chiếc Oppo cửa hàng bán được trong năm sau.
Học tốt Toán 8 Chương 9
Các bài học để học tốt Chương 9 Toán lớp 8 hay khác:
(199k) Xem Khóa học Toán 8 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 8 Chân trời sáng tạo hay khác:
Lý thuyết Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác
Lý thuyết Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Lý thuyết Toán 8 Bài 2: Xác suất lí thuyết và xác suất thực nghiệm
Xem thêm các tài liệu học tốt lớp 8 hay khác:
- Giải sgk Toán 8 Chân trời sáng tạo
- Giải SBT Toán 8 Chân trời sáng tạo
- Giải lớp 8 Chân trời sáng tạo (các môn học)
- Giải lớp 8 Kết nối tri thức (các môn học)
- Giải lớp 8 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải bài tập Toán 8 hay nhất, chi tiết của chúng tôi được biên soạn bám sát sgk Toán 8 Chân trời sáng tạo (Tập 1 & Tập 2) (NXB Giáo dục).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 8 (hay nhất) - CTST
- Soạn văn 8 (ngắn nhất) - CTST
- Giải sgk Toán 8 - CTST
- Giải Tiếng Anh 8 Global Success
- Giải sgk Tiếng Anh 8 Smart World
- Giải sgk Tiếng Anh 8 Friends plus
- Giải sgk Khoa học tự nhiên 8 - CTST
- Giải sgk Lịch Sử 8 - CTST
- Giải sgk Địa Lí 8 - CTST
- Giải sgk Giáo dục công dân 8 - CTST
- Giải sgk Tin học 8 - CTST
- Giải sgk Công nghệ 8 - CTST
- Giải sgk Hoạt động trải nghiệm 8 - CTST
- Giải sgk Âm nhạc 8 - CTST

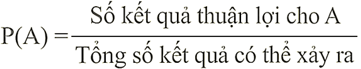



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

