Định lý cosin trong tam giác lớp 10 (chi tiết nhất)
Bài viết Định lý cosin trong tam giác lớp 10 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Định lý cosin trong tam giác.
Định lý cosin trong tam giác lớp 10 (chi tiết nhất)
1. Định lý cosin trong tam giác
Trong tam giác ABC với BC = a, AC = b, AB = c, ta có:
a2 = b2 + c2 – 2bc.cosA
b2 = a2 + c2 – 2ac.cosB
c2 = a2 + b2 – 2ab.cosC
2. Ví dụ minh họa về định lý cosin trong tam giác
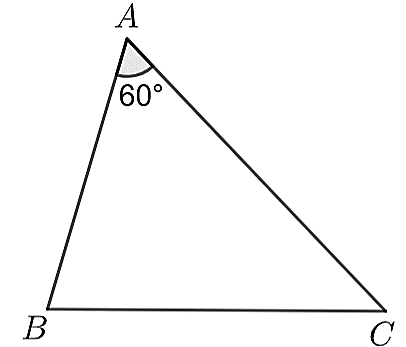
Ví dụ 1. Cho tam giác ABC có AB = 6 cm, AC = 8 cm và .
a) Tính độ dài cạnh BC.
b) Tính số đo góc B (làm tròn kết quả đến hàng phần mười của độ).
Hướng dẫn giải
a) Áp dụng định lý cosin vào tam giác ABC ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA = 62 + 82 – 2.6.8.cos60o = 52
Vậy BC = cm.
b) Ta có: . Vậy .
Ví dụ 2. Hai máy bay cùng xuất phát từ một sân bay A và bay theo hai hướng khác nhau, tạo với nhau góc 70 độ. Máy bay thứ nhất bay với vận tốc 600 km/h, máy bay thứ hai bay với vận tốc 800 km/h. Sau 2 giờ, hai máy bay cách nhau bao nhiêu km (làm tròn kết quả đến hàng đơn vị)? Biết rằng cả hai máy bay bay theo đường thẳng và sau 2 giờ bay đều chưa hạ cánh.
Hướng dẫn giải
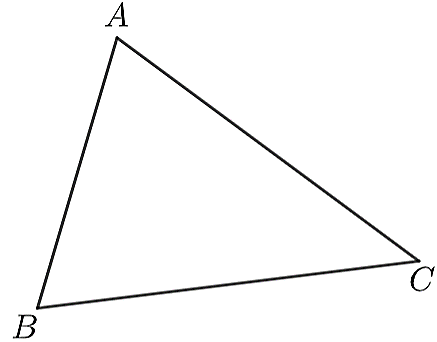
Sau 2 giờ, máy bay thứ nhất ở vị trí B, máy bay thứ hai ở vị trí C.
Ta có: AB = 2. 600 = 1200 km, AC = 2. 800 = 1600 km.
Ta có hình vẽ:
Áp dụng định lý cosin vào tam giác ABC ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA = 12002 + 16002 – 2.1200.1600.cos70o.
Do đó, BC 1639 (km).
Vậy sau hai giờ bay, hai máy bay cách nhau khoảng 1639 km.
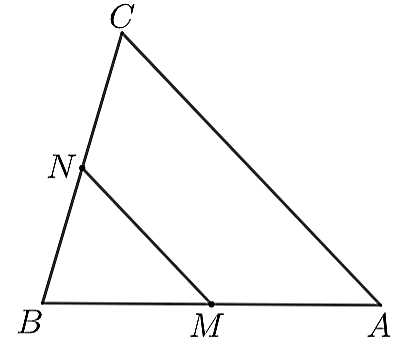
Ví dụ 3. Cho tam giác ABC có M, N lần lượt là trung điểm của AB, BC. Biết rằng BC = 6 cm, MN = 5 cm và = . Tính độ dài cạnh AB.
Hướng dẫn giải
Ta có: BN BC = 3 (cm).
Vì M, N lần lượt là trung điểm của AB, BC nên MN là đường trung bình của tam giác ABC. Do đó, = = .
Áp dụng định lý cosin vào tam giác BMN ta có:
BM2 = BN2 + MN2 – 2BN.MN.cos= 32 + 52 – 2.3.5.cos60o = 19
Vậy AB cm.
3. Bài tập về định lý cosin trong tam giác
Bài 1. Cho tam giác ABC có AB = 6 cm, AC = 12 cm, . Tính độ dài các cạnh và số đo các góc còn lại của tam giác ABC.
Bài 2. Một tam giác có độ dài ba cạnh là 5 cm, 6 cm, 7 cm. Tính góc nhỏ nhất của tam giác đó (làm tròn kết quả đến hàng phần trăm của độ).
Bài 3. Cho = . Gọi A, B lần lượt là 2 điểm di động lần lượt trên Om, On sao cho AB = 6 cm. Độ dài lớn nhất của OB bằng bao nhiêu cm?
Bài 4. Cho tam giác ABC thỏa mãn a2 + b2 = c2 + ab. Tính số đo góc A của tam giác ABC.
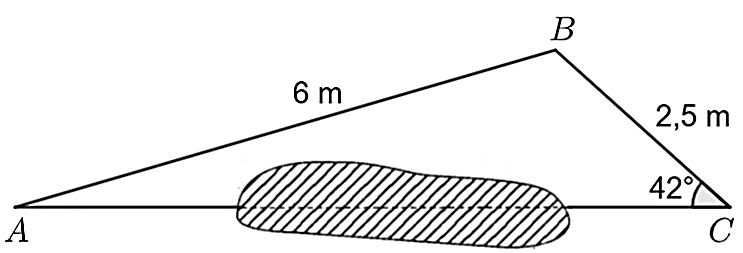
Bài 5. Khoảng cách từ A đến C không thể đo trực tiếp vì phải đi qua một đầm lầy nên người ta làm như sau: Xác định một điểm B sao cho AB = 6 m và đo được . Hãy tính khoảng cách AC biết rằng BC = 2,5 m.
Xem thêm các dạng bài tập Toán lớp 10 sách mới hay, chi tiết khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

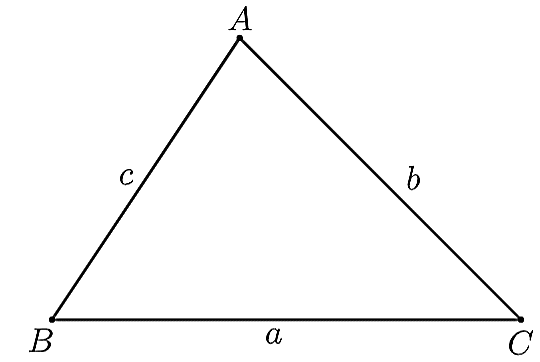



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

