Bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số lớp 12 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số lớp 12 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số.

Bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số lớp 12 (cách giải + bài tập)

1. Phương pháp giải

Đưa yêu cầu bài toán về mối quan hệ hàm số để tìm các đường tiệm cận của đồ thị hàm số.

2. Ví dụ minh họa

Ví dụ 1. Một tác giả muốn xuất bản một cuốn sách Toán học. Biết phí xuất bản là 7 triệu đồng và giá tiền in mỗi cuốn sách là 50 000 đồng. Gọi t (t ≥ 1) là số cuốn sách sẽ in và f(t) (đơn vị nghìn đồng) là chi phí trung bình của mỗi cuốn sách. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số f(t).

Hướng dẫn giải:

Tổng số tiền cần bỏ ra để in t cuốn sách là 7000 + 50t (nghìn đồng).

Chi phí trung bình của mỗi cuốn sách là f(t) = $\frac{7000+50t}{t}$.

Ta có $\underset{t\to +\infty }{\lim }f\left(t\right)$ = $\underset{t\to +\infty }{\lim }\frac{7000+50t}{t}$ = 50.

Vậy y = 50 là đường tiệm cận ngang của đồ thị hàm số f(t).

Ví dụ 2. Một bể chứa 2 m³ nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số f(t), thời gian t tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số f(t) là y = 19. Nồng độ muối trong bể sau khi bơm được 1 giờ là bao nhiêu?

Hướng dẫn giải:

Giả sử nước muối bơm vào có nồng độ a gam/lít.

Sau t phút, ta có khối lượng muối trong bể là 20at (gam).

Thể tích của lượng nước trong bể sau t phút là 2000 + 20t (lít).

Vậy nồng độ muối sau t phút là f(t) = $\frac{20at}{2000+20t}=\frac{at}{100+t}$ (gam/lít).

Ta có $\underset{t\to +\infty }{\lim }f\left(t\right)$ = $\underset{t\to +\infty }{\lim }\frac{at}{100+t}$ = a nên đồ thị hàm số y = f(t) có phương trình tiệm cận ngang là y = a = 10.

Từ đó hàm số nồng độ muối trong bể sau khi bơm được t phút là f(t) = $\frac{10t}{100+t}$.

Nồng độ muối sau 1 giờ bơm là f(60) = $\frac{10.60}{100+60}$ = 3,75 (gam/lít).

3. Bài tập tự luyện

Bài 1. Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số F(x) = 60000 + 250x. Gọi F(x) là hàm số biểu thị chi phí trung bình (đơn vị: nghìn đồng) để sản xuất x sản phẩm (x ≥ 0), khi đó tiệm cận ngang của đồ thị hàm số bằng

A. 250;

B. y = $\frac{1}{240}$;

C. y = 240;

D. y = 250.

Hướng dẫn giải:

Đáp án đúng là: D

Chi phí trung bình để sản xuất x sản phẩm là F(x) = $\frac{60000+250x}{x}$ (nghìn đồng).

Ta có $\underset{x\to +\infty }{\lim }F\left(x\right)$ = $\underset{x\to +\infty }{\lim }\frac{60000+250x}{x}$ = 250.

Bài 2. Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f(t) = $\frac{26t+10}{t+5}$; f(t) được tính bằng nghìn người. Xem f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang y = a. Giá trị của a là bao nhiêu?

A. 20;

B. 36;

C. 10;

D. 26.

Hướng dẫn giải:

Đáp án đúng là: D

Ta có $\underset{t\to \infty }{\lim }f\left(t\right)$ = $\underset{t\to \infty }{\lim }\frac{26t+10}{t+5}$ = 26. Nên đồ thị hàm số f(t) có đường tiệm cận ngang là y = 26.

Bài 3. Một nhà máy sản xuất linh kiện điện tử thống kê được rằng trung bình một tổ sản xuất với x người thì số sản phẩm sản xuất được trong một thời gian cố định được tính bằng công thức P(x) = $\frac{5000x}{4x+25}$. Xem y = P(x) là một hàm số xác định trên [0; +∞), khi đó tiệm cận ngang của đồ thị hàm số là:

A. y = 25;

B. x = 25;

C. x = 1250;

D. y = 1250.

Hướng dẫn giải:

Đáp án đúng là: D

Ta có $\underset{x\to \infty }{\lim }P\left(x\right)$ = $\underset{x\to \infty }{\lim }\frac{5000x}{4x+25}$ = $\underset{x\to \infty }{\lim }\frac{5000}{4+\frac{25}{x}}$ = 1250.

Vậy tiệm cận ngang của đồ thị hàm số là y = 1250.

Bài 4. Số lượng sản phẩm của công ty bán được trong x tháng được tính bởi công thức S(x) = 300(2 + $\frac{4}{x+2}$) với x ≥ 1. Xem y = S(x) là một hàm số xác định trên [1; +∞). Khi đó tiệm cận ngang của đồ thị hàm số là

A. y = 600;

B. x = 600;

C. x = 300;

D. y = 2400.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có $\underset{x\to +\infty }{\lim }S\left(x\right)=\underset{x\to +\infty }{\lim }300(2+\frac{4}{x+2})$ = 600.

Vậy tiệm cận ngang của đồ thị hàm số là y = 600.

Bài 5. Dân số P (nghìn người) của một khu nghỉ dưỡng được cho bởi hàm số P(t) = $\frac{400t}{2t^2+7}$, t ≥ 0 với t là thời gian tính theo tháng. Tìm tiệm cận ngang của đồ thị hàm số y = P(t).

A. y = 0;

B. y = 200;

C. x = 0;

D. y = $\frac{400}{7}$.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có $\underset{t\to \infty }{\lim }P\left(x\right)=\underset{t\to \infty }{\lim }\frac{400t}{2t^2+7}$ = $\underset{t\to \infty }{\lim }\frac{\frac{400}{t}}{2+\frac{7}{t}}$ = 0.

Do vậy tiệm cận ngang của đồ thị hàm số y = P(t) là đường thẳng y = 0.

Bài 6. Người ta thống kê được chi phí sửa chữa, vận hành máy móc trong một năm của một xưởng sản xuất được tính bởi công thức f(x) = $\frac{2000x+1500}{35x+5}$ (triệu đồng). Biết x là số năm kể từ lúc máy móc vận hành lần đầu tiên, số năm càng nhiều thì chi phí càng cao. Khi số năm x đủ lớn thì chi phí vận hành máy móc trong một năm gần với số nào? (làm tròn đến 1 chữ số thập phân sau dấu phẩy).

A. 57,1;

B. 51,7;

C. 42,9;

D. 400.

Hướng dẫn giải:

Đáp án đúng là: A

Ta có: $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{2000x-1500}{35x+5}$ = $\frac{2000}{35}=\frac{400}{7}$.

Do đó đồ thị hàm số y = f(x) nhận đường thẳng y = $\frac{400}{7}$ làm tiệm cận ngang, tức là khi số năm x càng lớn thì chi phí vận hành máy móc trong một năm càng tiến gần đến $\frac{400}{7}$$\approx$ 51,7 (triệu đồng).

Bài 7. Để thiết kế một bể cá không nắp có dạng hình hộp chữ nhật có chiều cao là 80 cm, thể tích là 12800 cm³. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 VNĐ/m² và loại kính để làm mặt đáy có giá thành 100000 VNĐ/m². Gọi x là chiều dài của đáy bể cá với (x > 0, x (m)); f(x) là hàm số xác định chi phí để hoàn thành bể cá. Đồ thị hàm số f(x) có bao nhiêu đường tiệm cận?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: B

Gọi y là chiều rộng của đáy bể cá (y > 0, m).

Ta có : 0,8xy = 0,0128 $\Rightarrow$ y = $\frac{0,016}{x}$ (m).

Giá thành bể cá được xác định theo hàm số:

f(x) = 2.0,8(x + $\frac{0,016}{x}$).70000 + 100000.x.$\frac{0,016}{x}$ (VNĐ)

$\Rightarrow$ f(x) = 112000(x + $\frac{0,016}{x}$) + 1600 (VNĐ)

$\Rightarrow$ f(x) = 112000x + 1600 + $\frac{1792}{x}$ (VNĐ).

Ta có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)$ = $\underset{x\to 0^{+}}{\lim }(112000x+1600+\frac{1792}{x})$ = +∞.

$\underset{x\to +\infty }{\lim }\left[f\right(x)-(112000x+1600\left)\right]$ = $\underset{x\to +\infty }{\lim }\frac{1792}{x}$ = 0.

Nên đồ thị hàm f(x) có tiệm cận đứng là x = 0; tiệm cận xiên là y = 112000x + 1600.

Bài 8. Số lượng sản phẩm bán được của một cửa hàng quần áo trong t tháng được cho bởi công thức: S(t) = 200($\frac{2}{3}-\frac{8}{2+t}$) với t ≥ 1. Xem y = S(t) là một hàm số xác định trên nửa khoảng [1; +∞), biết rằng tiệm cận ngang của đồ thị hàm số có dạng $\frac{a}{b}$, a, b ∈ ${\mathbb{N}}^{*}$, (a, b) = 1. Tính P = a – 2b.

A. 400;

B. 3;

C. 394;

D. 406.

Hướng dẫn giải:

Đáp án đúng là: C

Ta có: $\underset{x\to +\infty }{\lim }S\left(t\right)$ = $\underset{x\to +\infty }{\lim }200(\frac{2}{3}-\frac{8}{2+t})$ = 200.$\frac{2}{3}=\frac{400}{3}$ $\Rightarrow$ a = 400; b = 3.

Vậy P = a – 2b = 400 – 6 = 394.

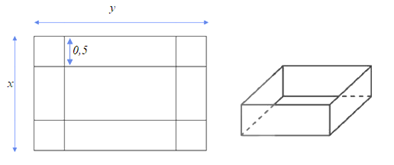
Bài 9. Từ một tấm tôn hình chữ nhật có các kích thước là x (m), y (m) với x > 1, y > 1 và diện tích bằng 4 m², người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng 0,5 m. Thể tích của thùng là hàm số V(x) trên khoảng (1; +∞). Đồ thị hàm số y = $\frac{1}{V\left(x\right)}$ có bao nhiêu đường tiệm cận đứng?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: B

Do tấm tôn có diện tích bằng 4 m² nên xy = 4 ⇔ y = $\frac{4}{x}$

Thùng có chiều cao là 0,5 m và các kích thước còn lại của thùng là: x – 1 và y – 1.

Thể tích của thùng là V(x) = 0,5.(x - 1)(y - 1) = $\frac{1}{2}$(x - 1)($\frac{4}{x}$ - 1) = $\frac{1}{2}$$\frac{(x-1)(4-x)}{x}$

Suy ra: y = $\frac{1}{V\left(x\right)}$ = $\frac{2x}{(x-1)(4-x)}$.

Ta có: $\underset{x\to 1^{+}}{\lim }\frac{1}{V\left(x\right)}$ = $\underset{x\to 1^{+}}{\lim }\frac{2x}{(x-1)(4-x)}$ = +∞ và $\underset{x\to 1^{-}}{\lim }\frac{1}{V\left(x\right)}$ = $\underset{x\to 1^{-}}{\lim }\frac{2x}{(x-1)(4-x)}$ = -∞

Suy ra đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số y = $\frac{1}{V\left(x\right)}$.

$\underset{x\to 4^{+}}{\lim }\frac{1}{V\left(x\right)}$ = $\underset{x\to 4^{+}}{\lim }\frac{2x}{(x-1)(4-x)}$ = -∞ và $\underset{x\to 4^{-}}{\lim }\frac{1}{V\left(x\right)}$ = $\underset{x\to 4^{-}}{\lim }\frac{2x}{(x-1)(4-x)}$ = +∞

Suy ra đường thẳng x = 4 là đường tiệm cận đứng của đồ thị hàm số y = $\frac{1}{V\left(x\right)}$.

Vậy đồ thị hàm số y = $\frac{1}{V\left(x\right)}$ có 2 đường tiệm cận đứng.

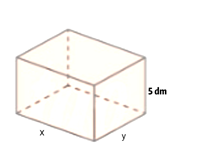
Bài 10. Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m³. Chiều cao của bể là 5 dm, các kích thước khác là x (m), y (m) với x > 0 và y > 0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0; +∞). Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a² + b² .

A. 5;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: A

Do thể tích của bể là 1 m³ nên 0,5xy = 1 ⇔ xy = 2.

Diện tích toàn phần của bể là S(x) = xy + 2.0,5.x + 2.0,5.y = 2 + x + $\frac{2}{x}$, (x > 0).

Ta có: $\underset{x\to +\infty }{\lim }\left(S\right(x)-(x+2\left)\right)$ = $\underset{x\to +\infty }{\lim }\frac{2}{x}$ = 0.

Suy ra đồ thị hàm số S(x) có đường tiệm cận xiên là y = x + 2 $\Rightarrow$ a = 1; b = 2.

Vậy P = a² + b² = 5.

Xem thêm các dạng bài tập Toán 12 hay, chi tiết khác:

• Tìm đường tiệm cận của đồ thị hàm số
• Một số bài toán về đường tiệm cận của đồ thị hàm số có chứa tham số
• Nhận dạng đồ thị hàm số
• Khảo sát sự biến thiên và vẽ đồ thị của hàm số
• Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn

---