Bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm số lớp 12 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm số lớp 12 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

Bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm số lớp 12 (cách giải + bài tập)

1. Phương pháp giải

Đưa yêu cầu bài toán về mối quan hệ hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số với điều kiện ràng buộc cho trước.

2. Ví dụ minh họa

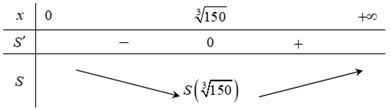
Ví dụ 1. Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200 m³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 350 nghìn đồng/m². Hãy xác định chi phí thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng).

Hướng dẫn giải:

Gọi chiều rộng của hình chữ nhật đáy bể là x (m) suy ra chiều dài của hình chữ nhật là 2x. Gọi h là chiều cao của bể ta có V = Sh = 2x².h = 200 $\Rightarrow$ h = $\frac{100}{x^2}$.

Diện tích của bể là S = 2h.x + 2.2hx + 2x² = 2x² + 6hx = 2x² + 6.$\frac{100}{x^2}$.x = 2x² + $\frac{600}{x}$.

S' = 4x - $\frac{600}{x^2}$

S' = 0 ⇔ 4x = $\frac{600}{x^2}$ ⇔ x = $\sqrt[3]{150}$.

Suy ra chi phí thấp nhất để xây bể là S($\sqrt[3]{150}$).350000 $\approx$ 59 triệu đồng.

Ví dụ 2. Một chất điểm chuyển động theo phương trình S = −t³ + 9t² + t + 10 trong đó t tính bằng giây và S tính bằng mét. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là bao nhiêu?

Hướng dẫn giải:

Ta có v(t) = s'(t) = −3t² + 18t + 1 = −3(t – 3)² + 28 ≤ 28 với mọi t ∈ ℝ.

Dấu “=” xảy ra khi t = 3.

Vậy thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là t = 3 giây.

3. Bài tập tự luyện

Bài 1. Một chất điểm chuyển động theo quy luật S(t) = 1 + 3t² – t³. Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu:

A. t = 2;

B. t = 1;

C. t = 3;

D. t = 4.

Hướng dẫn giải:

Đáp án đúng là: B

Ta có v(t) = S'(t) = −3t² + 6t = −3(t² – 2t + 1) + 3 = −3(t – 1)² + 3 ≤ 3.

Dấu “=” xảy ra khi t = 1.

Vậy vận tốc của chuyển động đạt giá trị lớn nhất bằng 3 khi t = 1.

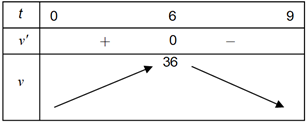
Bài 2. Một vật chuyển động theo quy luật s = $-\frac{1}{3}$t³ + 6t² với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

A. 243 (m/s);

B. 27 (m/s);

C. 144 (m/s);

D. 36 (m/s).

Hướng dẫn giải:

Đáp án đúng là: D

Ta có: v = s' = −t² + 12t; v' = −2t + 12; v' = 0 ⇔ t = 6.

Bảng biến thiên

Nhìn bảng biến thiên ta thấy vận tốc đạt giá trị lớn nhất khi t = 6.

Giá trị lớn nhất là v(6) = 36 m/s.

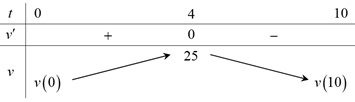
Bài 3. Một chất điểm chuyển động theo quy luật S = $-\frac{1}{3}$t³ + 4t² + 9t với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (mét) là quãng đường vật chuyển động trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu?

A. 88 m/s;

B. 25 m/s;

C. 100 m/s;

D. 11 m/s.

Hướng dẫn giải:

Đáp án đúng là: B

Ta có v = S' = −t² + 8t + 9, t ∈ (0; 10).

Có v' = −2t + 8; v' = 0 ⇔ t = 4 ∈ (0; 10).

Bảng biến thiên:

Vậy vận tốc lớn nhất của chất điểm là 25 m/s tại t = 4.

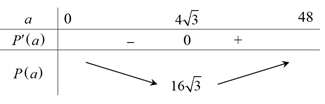
Bài 4. Trong tất cả các hình chữ nhật có cùng diện tích 48 cm², hình chữ nhật có chu vi nhỏ nhất bằng:

A. 16$\sqrt{3}$ cm;

B. 4$\sqrt{3}$ cm;

C. 24 cm;

D. 8$\sqrt{3}$ cm.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi cạnh của hình chữ nhật: a, b; 0 < a, b ≤ 48

Ta có: a.b = 48 ⇔ b = $\frac{48}{a}$. Chu vi: P(a) = 2(a + $\frac{48}{a}$).

Có P'(a) = 2(1 - $\frac{48}{a^2}$); P'(a) = 0 ⇔ a = 4$\sqrt{3}$.

Bảng biến thiên:

Vậy hình chữ nhật có chu vi nhỏ nhất là 16$\sqrt{3}$.

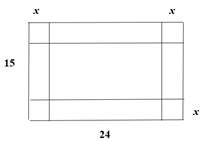
Bài 5. Cho một tấm nhôm hình chữ nhật có kích thước 15 cm × 24 cm. Người ta cắt bỏ 4 góc của tấm tôn 4 miếng hình vuông bằng nhau rồi gò lại thành một hình hộp chữ nhật không có nắp. Để thể tích của hình hộp đó lớn nhất thì độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng

A. 3 cm;

B. 4 cm;

C. 5 cm;

D. 2 cm.

Hướng dẫn giải:

Đáp án đúng là: A

Giả sử độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng x (0 < x < $\frac{15}{2}$).

Khi đó hình hộp chữ nhật có chiều cao bằng x, chiều rộng bằng 15 – 2x và chiều dài bằng 24 – 2x.

Suy ra hình hộp chữ nhật có thể tích V = x(15 – 2x)(24 – 2x) = 4x³ – 78x² + 360x.

Xét hàm f(x) = 4x³ – 78x² + 360x trên (0; $\frac{15}{2}$).

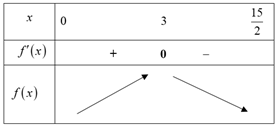
Có f'(x) = 12x² – 156x + 360 = 0 ⇔ x = 3 hoặc x = 10.

Bảng biến thiên

Dựa vào bảng biến thiên ta có hàm số đạt giá trị lớn nhất trên (0; $\frac{15}{2}$) tại x = 3 hay hình hộp chữ nhật có thể tích lớn nhất khi độ dài cạnh hình vuông của miếng tôn bị cắt bỏ bằng 3 cm.

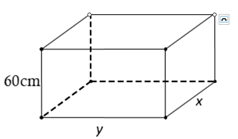
Bài 6. Để thiết kế một chiếc bể cá hình hộp chữ nhật không có nắp có chiều cao là 60 cm, thể tích 96000 cm³. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 đồng/m² và loại kính để làm mặt đáy có giá thành 100000 đồng/m². Chi phí thấp nhất để hoàn thành bể cá bằng

A. 83200 đồng;

B. 320000 đồng;

C. 832000 đồng;

D. 32000 đồng.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi x (m), y (m) (x > 0, y > 0) là chiều dài và chiều rộng của đáy bể.

Theo giả thiết ta có 0,6xy = 0,096 $\Rightarrow$ y = $\frac{4}{25x}$.

Ta có diện tích mặt đáy là xy = x.$\frac{4}{25x}$ = 0,16.

Giá tiền làm kính mặt đáy là 0,16.100000 = 16000 đồng.

Diện tích xung quanh bể là 2x.0,6 + 2y.0,6 = 1,2(x + $\frac{0,16}{x}$).

Giá tiền làm kính các mặt xung quanh là 1,2(x + $\frac{0,16}{x}$).70000 = 84000(x + $\frac{0,16}{x}$) (đồng).

Tổng chi phí là f(x) = 84000(x + $\frac{0,16}{x}$) + 16000 ≥ 84000.2$\sqrt{x.\frac{0,16}{x}}$ + 16000 = 83200 đồng.

Chi phí thấp nhất để hoàn thành bể cá bằng 83200 đồng.

Bài 7. Một loại thuốc được dùng cho một bệnh nhân với nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được tính theo công thức c(t) = $\frac{t}{t^2+1}$ . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?

A. 4 giờ;

B. 1 giờ;

C. 3 giờ;

D. 2 giờ.

Hướng dẫn giải:

Đáp án đúng là: B

Tập xác định: D = (0; +∞).

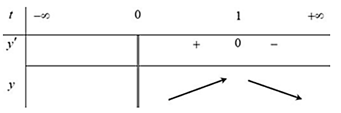
Có c'(t) = $\frac{1-t^2}{t^2+1}$; c'(t) = 0 ⇔ t = 1 (vì t > 0).

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bệnh nhân cao nhất.

Bài 8. Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là 6000 – 3x (nghìn đồng), x ∈ ℕ*, x < 2000 . Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?

A. 100;

B. 1000;

C. 200;

D. 2000.

Hướng dẫn giải:

Đáp án đúng là: B

Số tiền hãng thu được khi đại lí nhập x chiếc điện thoại là f(x) = x(6000 – 3x).

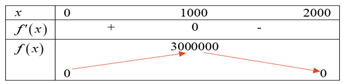
Ta có: f'(x) = −6x + 6000. Khi đó, f'(x) = 0 ⇔ x = 1000.

Bảng biến thiên của hàm số f(x) là:

Vậy đại lí nhập cùng lúc 1000 chiếc điện thoại thì hãng có thể thu nhiều tiền nhất từ đại lí đó với 3 000 000 (nghìn đồng).

Bài 9. Bạn Hoa cần gấp một hộp quà có dạng hình lăng trụ tứ giác đều với diện tích toàn phần là 200 cm². Hộp quà mà bạn Hoa gấp được có thể tích lớn nhất bằng bao nhiêu centimet khối (làm tròn kết quả đến hàng đơn vị)?

A. 192;

B. 129;

C. 219;

D. 291.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi độ dài cạnh đáy và chiều cao hộp quà lần lượt là x (cm) và y (cm) (x > 0, y > 0).

Theo giả thiết, ta có: 2x² + 4xy = 200 $\Rightarrow$ y = $\frac{50}{x}-\frac{x}{2}$ và x < 10 (vì y > 0).

Xét hàm số V(x) = x²($\frac{50}{x}-\frac{x}{2}$) = 50x - $\frac{1}{2}$x³ (0 < x < 0) là thể tích của hộp quà mà bạn Hoa gấp được.

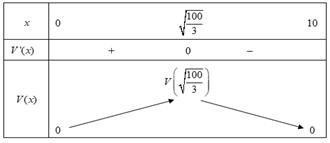
Ta có: V'(x) = 50 - $\frac{3}{2}$x² = 0 ⇔ x = $\pm \sqrt{\frac{100}{3}}$.

Bảng biến thiên của hàm số V(x) là:

Vậy bạn Hoa có thể gấp hộp quà có thể tích lớn nhất là V($\sqrt{\frac{100}{3}}$) $\approx$ 192 (cm³)

Bài 10. Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hàng một máy in trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy in chạy trong một giờ là 10(6n + 10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy in để được lãi nhiều nhất.

A. 5;

B. 6;

C. 7;

D. 8.

Hướng dẫn giải:

Đáp án đúng là: A

Giả sử có n máy in thì chi phí cố định là 50n (n = {1; 2; 3; …; 8}).

Để in 50000 tờ cần $\frac{50000}{3600n}=\frac{125}{9n}$ (giờ in).

Chi phí cho n máy chạy trong một giờ là 10(6n +10) nghìn đồng.

Khi đó tổng chi phí để in 50000 tờ quảng cáo là:

f(n) = 50n + $\frac{10(6n+10).125}{9n}$ = $\frac{450n^2+7500n+12500}{9n}$.

Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.

Thay các giá trị n ∈ {1; 2; 3; 4; 5; 6; 7; 8} ta thấy giá trị nhỏ nhất là f(5) = $\frac{12250}{9}$.

Xem thêm các dạng bài tập Toán 12 hay, chi tiết khác:

• Một số bài toán hàm hợp liên quan đến giá trị lớn nhất và giá trị nhỏ nhất của hàm số
• Sử dụng đồ thị hàm số hoặc bảng biến thiên xác định các đường tiệm cận
• Tìm đường tiệm cận của đồ thị hàm số
• Một số bài toán về đường tiệm cận của đồ thị hàm số có chứa tham số
• Một số bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số

---