Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2)
Bài viết Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2) với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2).
Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2)
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Bài giảng: Các phép biến đổi cơ bản trên tập hợp số phức - Cô Nguyễn Phương Anh (Giáo viên VietJack)
Cho |z + a| = |z + b| Tìm Max, min P với P = |z + z1| + |z + z2|
1. Phương pháp
Cách 1:
+) Bước 1: Khai triển |z + a| = |z + b| đưa về dạng đường thẳng
+) Bước 2 : Từ P ta tìm tọa độ điểm A ; B và xét vị trí tương đối của A ;B với d
+) Khi đó z là M thỏa mãn P min :
Cách 2:
Áp dụng
BĐT Bunhia Copski: (Ax + By)2 ≤ (A2 + B2)(x2 + y2) nếu tìm max
BĐT Mincopxki:
2. Ví dụ minh họa
Ví dụ 1: Cho số phức z thỏa mãn điều kiện |z - 1| = √2. Tìm giá trị lớn nhất của T = |z + i|+ |z - 2 - i|
A. maxT = 8√2 B. maxT = 4 C. maxT = 4√2 D. maxT = 8
Lời giải:
Áp dụng công thức độ dài đường trung tuyến ta có:
Theo bất đẳng thức Bunhiacopxki thì
T2 ≤ (|z + 1|2 + |z - 1|2)(12+ 12) = 16 => T ≤ 4
Chọn đáp án là B.
Ví dụ 2: Cho |z - i| + |z - 3 + 3i| = 6. Tính max min của P = |z - 6 + 7i|
Lời giải:
Cách 1: PP hình học
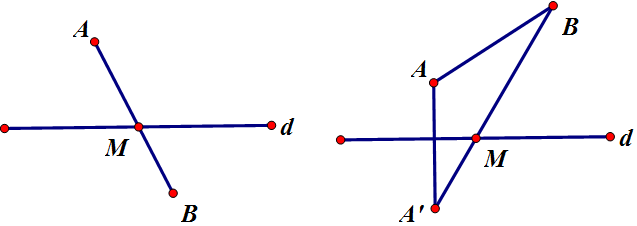
Nhắc lại: Gọi A và B là điểm biểu diễn z1; z2 và M là điểm biểu diễn z; C là điểm biểu diễn z3 trong P
Khi đó MA + MB = k
Nếu MA+ = AB thì điểm biểu diễn là đường thẳng
Nếu MA + MB > AB thì điểm biểu diễn là elip
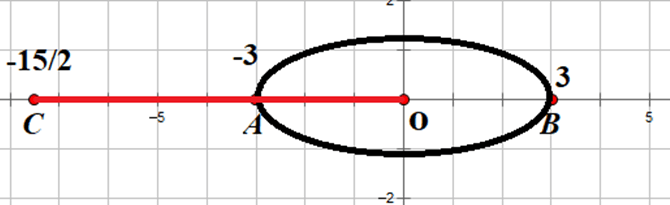
Khi đó ta vẽ hình biểu diễn các điểm A, B, C trên mặt Oxy và xác định M trong các trường hợp là đường thẳng hoặc elip sao cho MC ngắn nhất hoặc lớn nhất.
Lời giải
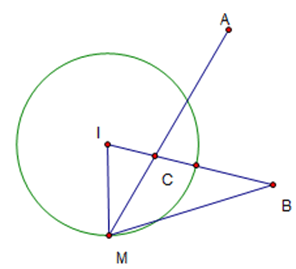
Gọi A(0; 1);B(3; -3);C(6; -7);M(x; y)
Khi đó MA + MB = 6; Tìm max min của MC
Ta thấy MA + MB > AB => Elip Trong đó I là trung điểm AB
Khi đó
MC min khi MC = B’C = BC - BB’ = BC - (a - c) = 5 - (1/2) = 4,5
MC max khi MC = A’C = AC + AA’ = AC + (a - c) = 10 + (1/2) = 10,5
Cách 2: Dùng máy tính CASIO
Ví dụ 3: Cho số phức z thỏa mãn |z - 2 - 3i| = 1. Giá trị nhỏ nhất của |z + 1 + i| là:
A. √13 - 1 B. 4 C. -4 D. √13 + 1
Lời giải:
Ta có:
|z + 1 + i| = |z + 1 -i| = |(z - 2 - 3i) + (3 + 2i)| ≥ ||z - 2 - 3i| - |3 + 2i|| = √13 - 1
Chọn đáp án là A.
Ví dụ 4: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức T = |z + 1| + 2|z - 1|
A. max T = 2√5 B. max T = 2√10 C. max T = 3√5 D. max T = 3√2
Lời giải:
Áp dụng công thức độ dài đường trung tuyến ta có:
Theo bất đẳng thức Bunhiacopxki thì:
T2 ≤ (|z + 1|2 |z - 1|2)(12 + 22) = 20 => T ≤ 2√5
Chọn đáp án là A.
Ví dụ 5: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức: T = |z + 1| + 3|z - 1|
A. max T = 3√10 B. max T = 2√10 C. max T = 6 D. max T = 4√2
Lời giải:
Áp dụng công thức trung tuyến ta có :
Theo bất đẳng thức Bunhiacopxki thì
T2 ≤ (|z + 1|2 + |z - 1|2)(12 + 32) = 40 => T ≤ 2√10
Chọn đáp án là B.
Ví dụ 6: Cho số phức z thay đổi và thỏa mãn |z - 1 - i| = 5. Tìm giá trị lớn nhất của biểu thức P = 2|z - 8i| - |z - 7 - 9i| bằng:
Lời giải:
Gọi M(x; y) biểu diễn số phức z, từ |z - 1 - i| = 5 thì M nằm trên đường tròn (x - 1)2 + (y - 1)2 = 25 có tâm và bán kính : I(1; 1), R = 5.
Gọi A(0; 8); B(7; 9) thì:
Phân tích : mục tiêu tìm tọa độ điểm sao cho MB = 2MC, nhận thấy IB = 2IM = 2R nên ta có hai cách tìm tọa độ điểm C như sau :
Cách 1 : (x - 1)2 + (y - 1)2 = 25 ⇔ T = x2 + y2 - 23 = 0
Nên chọn điểm 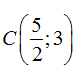
Cách 2 : Lấy điểm C thỏa mãn 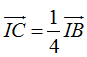
Ta có: P = 2MA - MB = 2(MA - MC) ≤ 2Ac = 5√5
Dấu "=" đạt được khi điểm C nằm trên đoạn AM.
Chọn B.
Ví dụ 7: Cho số phức z thoả mãn:
Giá trị lớn nhất của biểu thức: P = |z - 5 - 2i| bằng
A. √2 + 5√3 B. √2 + 3√5
C. √5 + 2√3 D. √5 + 3√2
Lời giải:
Cách 1: Đại số
Đặt z = a + bi
Từ giả thiết:
⇔ 2|a| + 2|b| = a2 + b2
⇔ (|a| - 1)2 + (|b| - 1)2 = 2 (1)
Ta có:
Dễ thấy P lớn nhất khi a, b ≤ 0. Khi đó:
Do a, b ≤ 0 nên từ (1) ta có: (a + 1)2 + (b + 1)2 = 2
Chọn B.
Cách 2: Hình học
Đặt z = a + bi.
Từ giả thiết
⇔ 2|a| + 2|b| = a2 + b2
⇔ (|a| - 1)2 + (|b| - 1)2 = 2 (1)
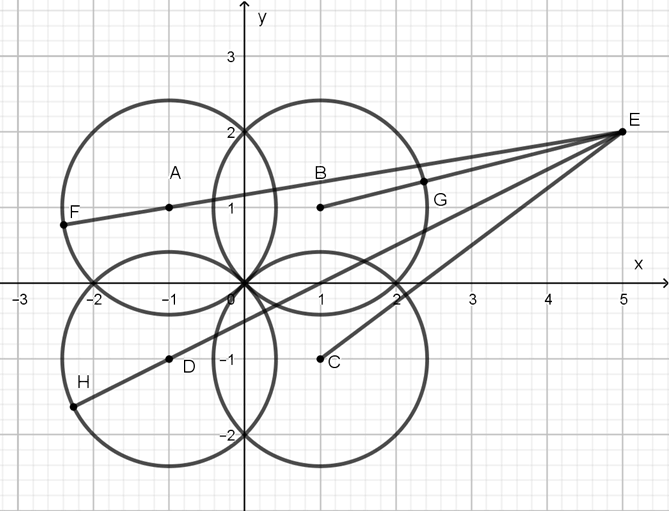
Tập hợp M biểu diễn z thuộc các phần đường tròn cùng bán kính là R = √2 có tâm là A(-1; 1), B(1; 1), C(1; -1), D(-1; -1) nằm chọn vẹn trong 1 góc phần tư (bỏ đi các cung nhỏ).
P = ME với E(5; 2). Từ hình vẽ ta thấy max P = HE = ED + √2 = 3√5 + √2
Ví dụ 8: Cho số phức z thỏa mãn
Tìm giá trị lớn nhất của biểu thức:
A. 10 B. 20 C. 2√5 D. 4√5
Lời giải:
Ta có:
Gọi M là điểm biểu diễn số phức, tập hợp điểm biểu diễn số phức z là đường tròn có phương trình:
(x - 2)2 + (y - 3)2 = 20 (C)
= |z + i| + 2|z - 4 - 7i|, A(0; -1); B(4; 7) lần lượt biểu diễn 2 số phức z1 = -i, z2 = 4 + 7i. Ta có A, B ∈ (C), AB = 4√5 = 2R nên nên AB là bán kính đường tròn (C)=> MA2 + MB2 = AB2 = 80
Mặt khác:
dấu “=” xảy ra khi MB = 2MA
Vậy maxP = 20
Chọn B.
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Xem thêm các dạng bài tập Toán lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:
- Dạng 1: Tìm giá trị lớn nhất, nhỏ nhất của môđun số phức
- Dạng 2: Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 1)
- Dạng 4: Tìm giá trị nhỏ nhất, lớn nhất của số phức (tổng hợp)
- Các dạng bài tập hay về số phức
- 18 Bài tập số phức hay và khó
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

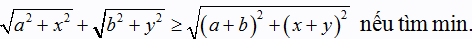
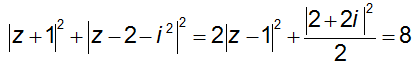
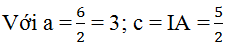
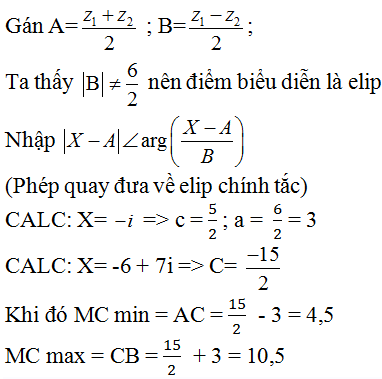
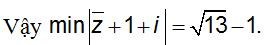
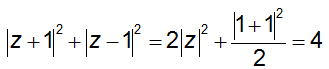
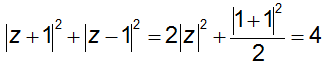

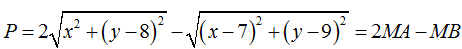
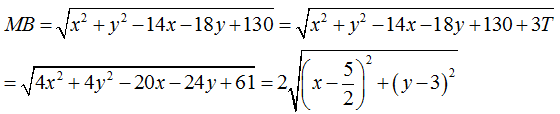
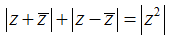
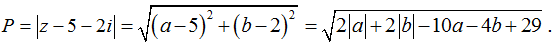
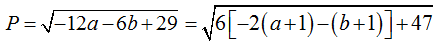
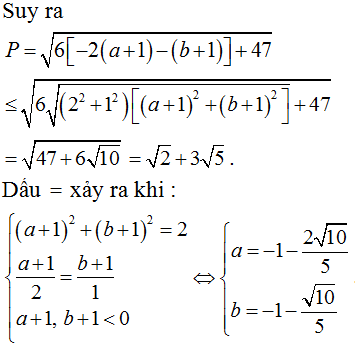
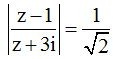
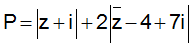
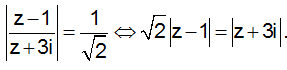
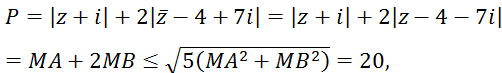



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

