Công thức Toán 10 Đại số cả năm (sách mới - đầy đủ)
Tổng hợp công thức Toán 10 Đại số đầy đủ học kì 1 & học kì 2 chi tiết nhất sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều như là cuốn sổ tay công thức giúp bạn học tốt môn Toán 10.
Công thức Toán 10 Đại số cả năm (sách mới - đầy đủ)
Công thức Mệnh đề. Tập hợp
Công thức Hàm số bậc hai và đồ thị
Công thức Thống kê
Công thức tính sai số tuyệt đối, sai số tương đối và độ chính xác
Công thức xác định số quy tròn và số gần đúng với độ chính xác cho trước
Công thức tính khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ
Công thức Xác suất
Các công thức về mệnh đề đảo, mệnh đề phủ định
1. Công thức
a) Mệnh đề đảo
- Cho mệnh đề kéo theo P ⇒ Q. Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q.
- Để xác định mệnh đề đảo, ta chỉ cần đảo vị trí hai mệnh đề P và Q với nhau.
b) Mệnh đề phủ định
Phủ định của một mệnh đề P là một mệnh đề kí hiệu là . Hai mệnh đề P và có tính đúng sai trái ngược nhau, tức là:
- Nếu P đúng thì sai.
- Nếu P sai thì đúng.
Ta có một số nguyên tắc để xác định mệnh đề phủ định của một mệnh đề như sau:
+ Phủ định của mệnh đề P là mệnh đề “không phải P”.
+ Phủ định của quan hệ = là quan hệ ≠ và ngược lại.
+ Phủ định của quan hệ > là quan hệ ≤ và ngược lại.
+ Phủ định của quan hệ < là quan hệ ≥ và ngược lại.
+ Phủ định liên kết “và” là liên kết “hoặc” và ngược lại.
+ Mệnh đề phủ định của “∀x ∈ X, P(x)” là: “∃x ∈ X, ”.
+ Mệnh đề phủ định của “∃x ∈ X, ” là “∀x ∈ X, P(x)”.
2. Ví dụ minh họa
Ví dụ 1. Phát biểu mệnh đề P ⇒ Q và phát biểu mệnh đề đảo, xét tính đúng sai của mỗi mệnh đề đảo đó.
a) P: “Tứ giác ABCD là hình thoi” và Q: “Tứ giác ABCD là hình vuông”;
b) P: “(– 3)2 > (– 5)2” và Q: “(– 3) > (– 5)”;
c) P: “Tam giác ABC cân tại A” và Q: “Tam giác ABC đều”.
Hướng dẫn giải:
a) - Mệnh đề P ⇒ Q được phát biểu như sau:
“ Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”.
- Mệnh đề đảo Q ⇒ P: “Tứ giác ABCD là hình vuông thì tứ giác ABCD là hình thoi”.
Mệnh đề đảo này là mệnh đề đúng, do hình vuông thì có 4 cạnh bằng nhau, 4 góc bằng nhau, hình thoi chỉ cần có 4 cạnh bằng nhau, vậy ABCD là hình vuông thì ABCD là hình thoi.
b) - Mệnh đề P ⇒ Q: “Nếu (– 3)2 > (– 5)2 thì (– 3) > (– 5)”.
- Mệnh đề đảo Q ⇒ P: “Nếu (– 3) > (– 5) thì (– 3)2 > (– 5)2”.
Do (– 3) > (– 5) luôn đúng và (– 3)2 = 9, (– 5)2 = 25, mà 9 < 25 nên (– 3)2 < (– 5)2, vậy mệnh đề đảo này là mệnh đề sai.
c) - Mệnh đề P ⇒ Q: “Nếu tam giác ABC cân tại A thì tam giác ABC đều”.
- Mệnh đề đảo Q ⇒ P: "Nếu tam giác ABC đều thì ABC là tam giác cân tại A".
Mệnh đề đảo này là mệnh đề đúng, do tam giác ABC đều thì tam giác này có ba cạnh bằng nhau hay AB = AC = BC, mà AB = AC nên tam giác ABC cân tại A.
Ví dụ 2. Cho mệnh đề P: “∀x ∈ ℝ, x2 + 1 > 0”. Phát biểu mệnh đề P, mệnh đề phủ định của mệnh đề P và xét tính đúng sai của mệnh đề phủ định đó.
Hướng dẫn giải:
- Mệnh đề P: “∀x ∈ ℝ, x2 + 1 > 0” được phát biểu là: “Với mọi số thực, tổng bình phương của nó với 1 luôn dương”.
- Mệnh đề phủ định của mệnh đề P là : “∃x ∈ ℝ, x2 + 1 ≤ 0”, mệnh đề này được phát biểu là: “Tồn tại một số thực sao cho tổng bình phương của nó với 1 luôn không dương”.
Ta có: x2 ≥ 0 ∀x ∈ ℝ nên suy ra x2 + 1 ≥ 0 + 1 = 1 > 0 ∀x ∈ ℝ.
Vậy mệnh đề P là mệnh đề đúng, do đó mệnh đề là mệnh đề sai.
................................
................................
................................
Các công thức về tập hợp và các phép toán trên tập hợp
1. Công thức
1.1. Tập hợp
a) Cách cho một tập hợp
Cách 1: Liệt kê các phần tử của tập hợp.
Cách 2: Nêu tính chất đặc trưng cho các phần tử của tập hợp.
b) Kí hiệu thuộc “∈” và không thuộc “∉”
Nếu a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là a thuộc A).
Nếu a không là một phần tử của tập hợp A, ta viết a ∉ A (đọc là a không thuộc A).
c) Tập rỗng
Một tập hợp có thể không chứa phần tử nào. Ta gọi đó là tập rỗng, kí hiệu là ∅.
Ta có: n(∅) = 0.
d) Tập con
Cho 2 tập hợp A, B, nếu mọi phần tử của B đều là phần tử của A thì ta nói tập hợp B là tập con của tập hợp A. Kí hiệu: B ⊂ A.
+) B ⊂ A ⇔∀x : x ∈ B ⇒ x ∈ A.
+) Nếu A ⊂ B, B ⊂ C thì A ⊂ C.
+) A ⊂ A; ∅⊂ A với mọi tập hợp A.
+) Tập hợp A có n phần tử thì số tập con của A là 2n.
+) Quan hệ giữa các tập hợp số: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.
e) Hai tập hợp bằng nhau
Hai tập hợp A và B bằng nhau nếu A là tập con của B và đồng thời B cũng là tập con của A. Kí hiệu: A = B.
+) A = B ⇔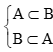
f) Một số tập con thường dùng của tập số thực ℝ.
Cho a, b là các số thực và a < b, ta có:
Trong đó: +∞ là dương vô cực (dương vô cùng);–∞ là âm vô cực (âm vô cùng).
1.2. Các phép toán trên tập hợp
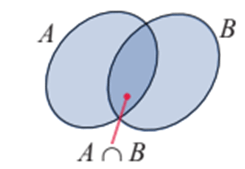
a) Giao của hai tập hợp
A ∩ B = {x | x ∈ A và x ∈ B}.
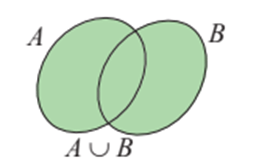
b) Hợp của hai tập hợp
A ∪ B = {x | x ∈ A hoặc x ∈ B}.
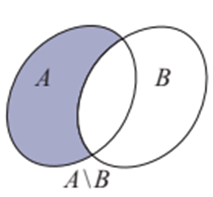
c) Hiệu của hai tập hợp, phần bù của tập con
+) Hiệu của hai tập hợp A và B: A \ B = {x | x ∈ A và x ∉ B}.
+) Chú ý:
• A \ A = ∅; A \ ∅ = A.
• A \ B ≠ B \ A (Vì B \ A ={x | x ∈ B và x ∉ A}.
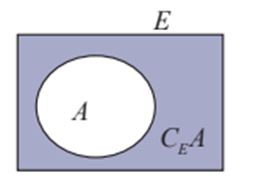
+) Phần bù của tập con: A ⊂ E ⇒ CEA = E \ A ={x | x ∈ E và x ∉ A} (phần bù của A trong E).
2. Ví dụ minh họa
Ví dụ 1. Cho hai tập hợp A = {x ∈ ℝ, x2 – 5 = 0} và B = {}. Tập hợp nào là tập con của tập hợp còn lại. Chúng có bằng nhau không?
Hướng dẫn giải:
Ta có: x2 – 5 = 0 ⇔ x2 = 5 ⇔ x = hoặc x = .
Do x ∈ ℝ, nên cả hai giá trị trên đều thỏa mãn.
Vậy A = {}.
Ta thấy mọi phần tử của tập hợp A đều là phần tử của tập hợp B nên A ⊂ B.
Và mọi phần tử của tập hợp B đều là phần tử của tập hợp A nên B ⊂ A.
Vậy A = B.
Ví dụ 2. Cho tập hợp A = {1; 2; 25; 30}, tập hợp B = {1; 2; 30} và tập hợp C = {2; 25; 28; 30}. Tìm các tập hợp A ∩ C, A ∪ C, CAB và A \ C.
Hướng dẫn giải:
Ta có: A ∩ C = {x | x ∈ A và x ∈ C} = {2; 25; 30}.
A ∪ C = {x | x ∈ A hoặc x ∈ C} = {1; 2; 25; 28; 30}.
Do mọi phần tử của tập hợp B đều là phần tử của tập hợp A nên B ⊂ A.
Khi đó: CAB = A \ B = {x | x ∈ A và x ∉ B} = {25}.
Ta có: A \ C = {x | x ∈ A và x ∉ C} = {1}.
................................
................................
................................
Lưu trữ: Công thức Toán 10 Đại số (sách cũ)
Công thức giải nhanh Toán lớp 10 Chương 3 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 4 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 5 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 6 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 3 Đại số
Các công thức về phương tình bậc hai: ax2 + bx + c = 0 (a ≠ 0)
1. Công thức nghiệm của phương trình bậc hai: Δ = b2 - 4ac
Δ < 0: Phương trình vô nghiệm
Δ = 0: Phương trình có nghiệm kép
x1 = x2 = - 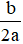
Δ > 0: Phương trình có 2 nghiệm phân biệt
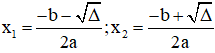
2. Công thức nghiệm thu gọn của phương trình bậc hai
Nếu b chẵn ta dùng công thức nghiệm thu gọn
Δ' = b'2 - ac
Δ' < 0: Phương trình vô nghiệm
Δ' = 0: Phương trình có nghiệm kép
x1 = x2 = -
Δ' > 0: Phương trình có 2 nghiệm phân biệt
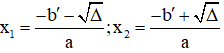
3. Định lý Vi-ét:
Nếu phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm x1; x2 thì

4. Các trường hợp đặc biệt của phương trình bậc hai:
- Nếu a + b + c = 0 thì phương trình có nghiệm: 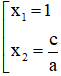
- Nếu a - b + c = 0 thì phương trình có nghiệm: 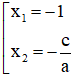
5. Dấu của nghiệm số: ax2 + bx + c = 0 (a ≠ 0)
- Phương trình có hai nghiệm trái dấu: x1 < 0 < x2 ⇔ P < 0
- Phương trình có hai nghiệm dương phân biệt: 0 < x1 < x2
⇔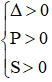
- Phương trình có hai nghiệm âm phân biệt x1 < x2 < 0
⇔
Công thức giải nhanh Toán lớp 10 Chương 4 Đại số
1. Bất đẳng thức
a) Các tính chất cơ bản của bất đẳng thức
+ Tính chất 1 (tính chất bắc cầu): a > b và b > c ⇔ a > c
+ Tính chất 2 (liên hệ giữa thứ tự và phép cộng): a > b ⇔ a + c > b + c (cộng hai vế của bất đẳng thức với cùng một số ta được bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho).
Hệ quả (Quy tắc chuyển vế): a > b + c ⇔ a - c > b
+ Tính chất 3 (quy tắc cộng): 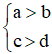
+ Tính chất 4 (liên hệ giữa thứ tự và phép nhân)
a > b ⇔ a.c > b.c nếu c > 0
Hoặc a > b ⇔ a.c < b.c nếu c < 0
+ Tính chất 5 (quy tắc nhân): 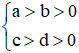
(Nhân hai vế tương ứng của 2 bất đẳng thức cùng chiều ta được một bất đẳng thức cùng chiều)
Hệ quả (quy tắc nghịch đảo): a > b > 0 ⇒
+ Tính chất 6: a > b > 0 ⇒ an > bn (n nguyên dương)
+ Tính chất 7: a > b > 0 ⇒ 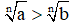
b) Bất đẳng thức Cauchy (Cô-si)
Định lí: Trung bình cộng của hai số không âm lớn hơn hoặc bằng trung bình nhân của chúng.
Nếu a ≥ 0, b ≥ 0 thì 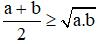
Dấu "=" xảy ra khi và chỉ khi a = b.
Hệ quả 1: Nếu 2 số dương có tổng không đổi thì tích của chùng lớn nhất khi 2 số đõ bẳng nhau.
Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
Hệ quả 2: Nếu 2 số dương có tích không đổi thì tổng của chùng nhỏ nhất khi 2 số đó bằng nhau.
Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng diện tích hình vuông có chu vi nhỏ nhất.
+ Bất đẳng thức Cô-si cho n số không âm a1; a2; …; an (n ∈ N*, n ≥ 2
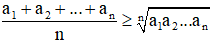
Dấu "=" xảy ra khi và chỉ khi a1 = a2 = … = an
c) Bất đẳng thức chứa dấu giá trị tuyệt đối
Định lý: Với mọi số thực a và b ta có:
|a + b| ≤ |a| + |b|
||a| - |b|| ≤ |a - b|
Dấu "=" xảy ra khi và chỉ khi ab ≥ 0.
d) Một số bất đẳng thức khác
+) x2 ≥ 0 ∀x ∈ R
+) [a] + [b] ≤ [a + b]
Trong đó [x] gọi là phần nguyên của số x, là số nguyên lớn nhất không lớn hơn x:
[x] ≤ x < [x] + 1
+) (a2 + b2)(x2 + y2) ≥ (ax + by)2 ∀a, b, x, y ∈ R.
2. Các công thức về dấu của đa thức
a) Dấu của nhị thức bậc nhất
Nhị thức bậc nhất f(x) = ax + b (a ≠ 0)cùng dấu với hệ số a khi x > 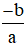
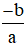
b) Dấu của tam thức bậc hai
f(x) = ax2 + bx + c (a ≠ 0)
Biệt thức Δ = b2 - 4ac
Δ < 0: f(x) cùng dấu với hệ số a
Δ = 0: f(x) cùng dấu với hệ số a với mọi x ≠
Δ > 0: f(x) có hai nghiệm x1; x2 (x1 < x2)
x |
- ∞ |
x1 |
x2 |
+ ∞ |
|||
f(x) |
cùng dấu a |
0 |
trái dấu a |
0 |
cùng dấu a |
*) Các công thức về điều kiện để tam thức bậc hai không đổi dấu trên R.
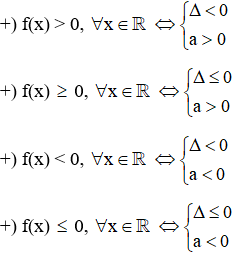
c) Dấu của đa thức bậc lớn hơn hoặc bằng 3. Bắt đầu ô bên phải cùng dấu với hệ số a của số mũ cao nhất, qua nghiệm đơn đổi dấu, qua nghiệm kép không đổi dấu.
3. Các công thức về phương trình và bất phương trình chứa dấu trị tuyệt đối
a) Phương trình
b) Bất phương trình
|A| < |B| ⇔ A2 < B2 ⇔ A2 - B2 < 0 ⇔ (A - B)(A + B) < 0
|A| ≤ |B| ⇔ A2 ≤ B2 ⇔ A2 - B2 ≤ 0
4) Các công thức về phương trình và bất phương trình chứa dấu căn bậc hai
a) Phương trình
b) Bất phương trình
Xem thêm tổng hợp công thức môn Toán lớp 10 đầy đủ và chi tiết khác:
Công thức giải nhanh Toán lớp 10 Chương 1 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 2 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 10 Chương 3 Hình học chi tiết nhất
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)


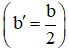
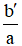
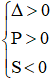
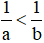
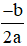
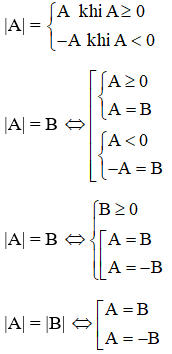
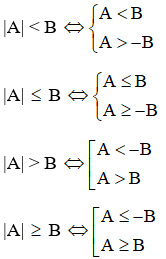
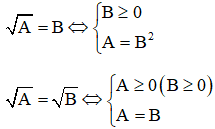
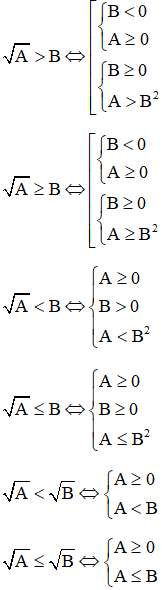






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

