Các công thức về tập hợp và các phép toán trên tập hợp (hay, chi tiết)

Bài viết Các công thức về tập hợp và các phép toán trên tập hợp chương trình sách mới trình bày đầy đủ công thức, ví dụ minh họa có lời giải chi tiết và các bài tập tự luyện giúp học sinh nắm vững kiến thức trọng tâm về Các công thức về tập hợp và các phép toán trên tập hợp từ đó học tốt môn Toán.

Các công thức về tập hợp và các phép toán trên tập hợp (hay, chi tiết)

1. Công thức

1.1. Tập hợp

a) Cách cho một tập hợp

Cách 1: Liệt kê các phần tử của tập hợp.

Cách 2: Nêu tính chất đặc trưng cho các phần tử của tập hợp.

b) Kí hiệu thuộc “∈” và không thuộc “∉”

Nếu a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là a thuộc A).

Nếu a không là một phần tử của tập hợp A, ta viết a ∉ A (đọc là a không thuộc A).

c) Tập rỗng

Một tập hợp có thể không chứa phần tử nào. Ta gọi đó là tập rỗng, kí hiệu là ∅.

Ta có: n(∅) = 0.

d) Tập con

Cho 2 tập hợp A, B, nếu mọi phần tử của B đều là phần tử của A thì ta nói tập hợp B là tập con của tập hợp A. Kí hiệu: B ⊂ A.

+) B ⊂ A ⇔∀x : x ∈ B ⇒ x ∈ A.

+) Nếu A ⊂ B, B ⊂ C thì A ⊂ C.

+) A ⊂ A; ∅⊂ A với mọi tập hợp A.

+) Tập hợp A có n phần tử thì số tập con của A là 2ⁿ.

+) Quan hệ giữa các tập hợp số: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

e) Hai tập hợp bằng nhau

Hai tập hợp A và B bằng nhau nếu A là tập con của B và đồng thời B cũng là tập con của A. Kí hiệu: A = B.

+) A = B ⇔.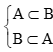

f) Một số tập con thường dùng của tập số thực ℝ.

Cho a, b là các số thực và a < b, ta có:

Trong đó: +∞ là dương vô cực (dương vô cùng);–∞ là âm vô cực (âm vô cùng).

1.2. Các phép toán trên tập hợp

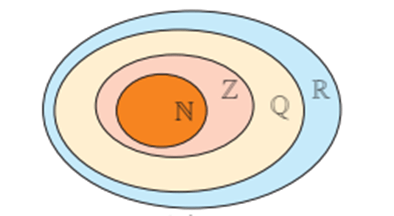
a) Giao của hai tập hợp

A ∩ B = {x | x ∈ A và x ∈ B}.

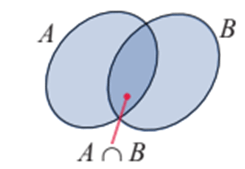
b) Hợp của hai tập hợp

A ∪ B = {x | x ∈ A hoặc x ∈ B}.

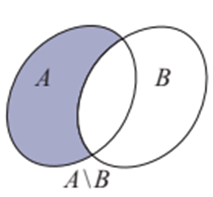
c) Hiệu của hai tập hợp, phần bù của tập con

+) Hiệu của hai tập hợp A và B: A \ B = {x | x ∈ A và x ∉ B}.

+) Chú ý:

• A \ A = ∅; A \ ∅ = A.

• A \ B ≠ B \ A (Vì B \ A ={x | x ∈ B và x ∉ A}.

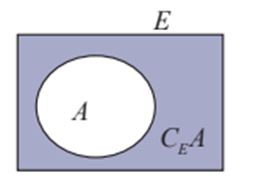
+) Phần bù của tập con: A ⊂ E ⇒ C_EA = E \ A ={x | x ∈ E và x ∉ A} (phần bù của A trong E).

2. Ví dụ minh họa

Ví dụ 1. Cho hai tập hợp A = {x ∈ ℝ, x² – 5 = 0} và B = {$-\sqrt{5};\sqrt{5}$}. Tập hợp nào là tập con của tập hợp còn lại. Chúng có bằng nhau không?

Hướng dẫn giải:

Ta có: x² – 5 = 0 ⇔ x² = 5 ⇔ x = $-\sqrt{5}$hoặc x = $\sqrt{5}$.

Do x ∈ ℝ, nên cả hai giá trị trên đều thỏa mãn.

Vậy A = {$-\sqrt{5};\sqrt{5}$}.

Ta thấy mọi phần tử của tập hợp A đều là phần tử của tập hợp B nên A ⊂ B.

Và mọi phần tử của tập hợp B đều là phần tử của tập hợp A nên B ⊂ A.

Vậy A = B.

Ví dụ 2. Cho tập hợp A = {1; 2; 25; 30}, tập hợp B = {1; 2; 30} và tập hợp C = {2; 25; 28; 30}. Tìm các tập hợp A ∩ C, A ∪ C, C_AB và A \ C.

Hướng dẫn giải:

Ta có: A ∩ C = {x | x ∈ A và x ∈ C} = {2; 25; 30}.

A ∪ C = {x | x ∈ A hoặc x ∈ C} = {1; 2; 25; 28; 30}.

Do mọi phần tử của tập hợp B đều là phần tử của tập hợp A nên B ⊂ A.

Khi đó: C_AB = A \ B = {x | x ∈ A và x ∉ B} = {25}.

Ta có: A \ C = {x | x ∈ A và x ∉ C} = {1}.

Ví dụ 3. Xác định các tập hợp sau đây:

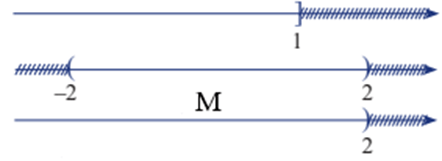
a) M = (–∞; 1] ∪ (– 2; 2);

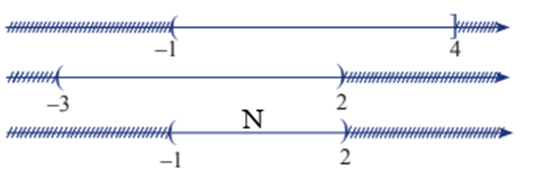
b) N = (– 1; 4] ∩ (– 3; 2);

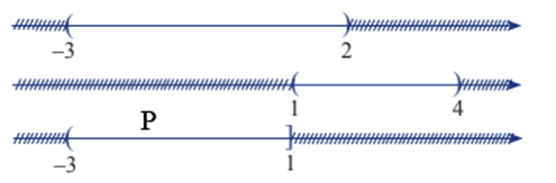
c) P = (– 3; 2) \ (1; 4).

Hướng dẫn giải

Để xác định các tập hợp M, N, P, ta vẽ sơ đồ biểu diễn các khoảng và nửa khoảng lên trục số như sau:

a)

Từ sơ đồ, ta thấy M = (– ∞; 2).

b)

Từ sơ đồ, ta thấy N = (– 1; 2).

c)

Từ sơ đồ, ta thấy P = (– 3; 1].

3. Bài tập tự luyện

Bài 1. Cho tập hợp A gồm các số tự nhiên là ước của 50. Viết tập hợp A bằng 2 cách. Cho các khẳng định sau, khẳng định nào đúng, khẳng định nào sai.

a) 2 ∈ A;

b) 15 ∈ A;

c) 25 ∉ A.

Bài 2. Trong mỗi cặp tập hợp sau đây, tập nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?

a) A = {5; 6; 7; 8}, B = {x ∈ ℤ | 4 < x ≤ 8};

b) H là tập hợp các tam giác cân, K là tập hợp các tam giác đều;

c) E = (1; 5) và F = (0; + ∞).

Bài 3. Cho tập hợp M = {a; b; c; d}. Tập M có bao nhiêu tập con?

Bài 4. Cho tập hợp C = {45; 7; 5; 25; 12} và tập hợp D = {5; 14; 7; 23}. Tìm C ∩ D; C ∪ D; C \ D.

Bài 5. Xác định các tập hợp sau đây:

a) (1; 4) ∪ (– 5; 7];

b) (–∞; 5) ∩ [– 3; 2);

c) [5; 200] \ (– 5; 20);

d) C_ℝA, với A = (– 6; 20].

Xem thêm các bài viết về công thức Toán hay, chi tiết khác:

• Công thức xác định tập xác định của hàm số

• Công thức xét tính đồng biến, nghịch biến của hàm số

• Công thức xác định tọa độ đỉnh, trục đối xứng của đồ thị hàm số bậc hai

• Công thức lượng giác của hai góc phụ nhau, bù nhau

• Các công thức lượng giác cơ bản

---