Tổng hợp công thức Toán 7 (cả năm - sách mới)
Việc nhớ chính xác một công thức Toán 7 trong hàng trăm công thức không phải là việc dễ dàng. Bài viết tổng hợp kiến thức, công thức Toán 7 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ Học kì 1, Học kì 2 như là cuốn sổ tay công thức giúp bạn học tốt môn Toán 7.
Tổng hợp công thức Toán 7 (cả năm - sách mới)
Xem Khóa học Toán 7 KNTT Xem Khóa học Toán 7 CTST Xem Khóa học Toán 7 CD
Công thức Toán 7 Kết nối tri thức
Công thức Toán 7 Chân trời sáng tạo
Công thức Toán 7 Cánh diều
Tổng hợp Công thức Toán 7 Học kì 1
Công thức Toán 7 Chương 1 Số hữu tỉ
Công thức Toán 7 Chương 2 Số thực
Công thức Toán 7 Tỉ lệ thức
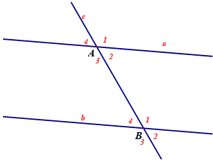
Công thức Toán 7 Góc và hai đường thẳng song song
Công thức Toán 7 Hình học trực quan
Tổng hợp Công thức Toán 7 Học kì 2
Công thức Toán 7 Tam giác bằng nhau
Công thức Trường hợp bằng nhau thứ nhất của tam giác cạnh cạnh cạnh
Công thức Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh
Công thức Trường hợp bằng nhau thứ ba của tam giác góc cạnh góc
Công thức Toán 7 Quan hệ giữa các yếu tố trong một tam giác
Công thức Toán 7 Biểu thức đại số
Công thức Toán 7 Xác suất
Công thức tính xác suất của biến cố chắc chắn, biến cố không thể và các biến cố đồng khả năng
Công thức tính xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
Công thức cộng, trừ, nhân, chia số hữu tỉ
1. Công thức
a) Cộng và trừ hai số hữu tỉ
Trường hợp 1: Hai phân số cùng mẫu số
Viết hai số hữu tỉ x, y dưới dạng (a, b, m, n ∈ ℤ, m ≠ 0)
Khi đó ta có:
;
.
Trường hợp 2: Hai phân số khác mẫu số
Viết hai số hữu tỉ x, y dưới dạng (a, b, m, n ∈ℤ, m, n ≠ 0)
Khi đó ta có:
;
.
Tính chất: Phép cộng số hữu tỉ cũng có các tính chất của phép cộng phân số:
- Tính chất giao hoán: x + y = y + x
- Tính chất kết hợp: (x + y) + z = x + (y + z)
- Tính chất cộng với 0:x + 0 = x
b) Nhân hai số hữu tỉ
Với hai số hữu tỉ (b, d ≠ 0) ta có:
.
Tính chất: Phép nhân trong ℚ có các tính chất cơ bản sau:
- Tính chất giao hoán: a. b = b. a
- Tính chất kết hợp: (a. b). c = a. (b. c)
- Nhân với 1: a. 1 = a
- Tính chất phân phối của phép nhân đối với phép cộng: a. (b + c) = a. b + a. c
c) Chia hai số hữu tỉ
Với hai số hữu tỉ (b, d, y ≠ 0) ta có:
.
2. Ví dụ minh họa
Ví dụ 1. Thực hiện phép tính:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải:
a)
;
b)
.
c)
.
d)
.
Ví dụ 2. Thực hiện phép tính:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải:
a)
;
b)
;
c)
;
d)
.
................................
................................
................................
Công thức lũy thừa với số mũ tự nhiên
1. Công thức
a) Lũy thừa với số mũ tự nhiên
(x ∈ ℚ, n ∈ ℕ, n > 1);
Nếu (a, b ∈ ℤ, b ≠ 0) thì:
.
Quy ước:
(x ∈ ℚ, x ≠ 0);
(x ∈ ℚ).
b) Nhân hai lũy thừa cùng cơ số
xm .xn = xm+n (x ℚ, m, n ℕ);
c) Chia hai lũy thừa cùng cơ số
xm : xn = xm-n (x ≠ 0, m ≥ n);
d) Lũy thừa của lũy thừa
= xm.n (x ℚ, m, n ℕ).
2. Ví dụ minh họa
Ví dụ 1. Tính:
a) (–3)3;
b) ;
c) ;
d) .
Hướng dẫn giải:
a) (–3)3 = (–3).(–3).(–3)= –27;
b)
;
c)
;
d)
Ví dụ 2. Viết các biểu thức dưới dạng lũy thừa:
Hướng dẫn giải:
................................
................................
................................
Lưu trữ: Công thức Toán 7 (sách cũ)
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

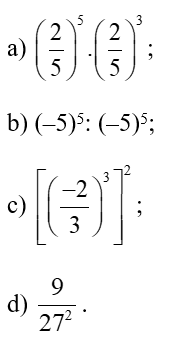
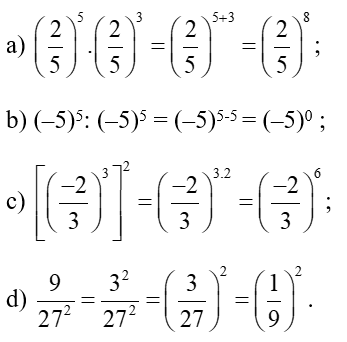
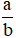 với a, b ∈ Z, b ≠ 0
với a, b ∈ Z, b ≠ 0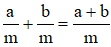
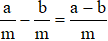

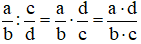
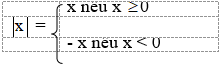
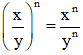 (y ≠ 0)
(y ≠ 0)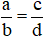 .
.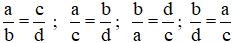

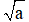 và một số âm kí hiệu là -
và một số âm kí hiệu là -
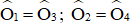
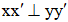 .
.






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

