(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Thống kê và xác suất
Chuyên đề Thống kê và xác suất trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Thống kê và xác suất
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
I. LÝ THUYẾT CẦN NHỚ
1. Các số đặc trưng của mẫu số liệu không ghép nhóm
1.1. Các số đặc trưng đo xu thế trung tâm
a) Số trung bình
• Giả sử ta có một mẫu số liệu là x1, x2, ..., xn. Cỡ mẫu của dãy số liệu là n.
Số trung bình (hay số trung bình cộng) của mẫu số liệu này, kí hiệu , được tính bởi công thức
• Giả sử mẫu số liệu được cho dưới dạng bảng tần số
Giá trị |
x1 |
x2 |
… |
xk |
Tần số |
n1 |
n2 |
… |
nk |
Bảng 1
Khi đó, công thức tính số trung bình trở thành
trong đó cỡ mẫu n1 + n2 + ... + nk.
• Kí hiệu là tần số tương đối (hay còn gọi là tần suất) của xk trong mẫu số liệu. Khi đó, số trung bình còn có thể biểu diễn là = f1x1 + f2x2 + ... + fkxk.
Ý nghĩa: Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
b) Trung vị
Sắp xếp lại mẫu số liệu là x1, x2, ..., xn theo thứ tự không giảm, ta được dãy
Số trung vị của mẫu số liệu trên là giá trị ở chính giữa dãy x1, x2, ..., xn. Cụ thể:
– Nếu n = 2k + 1, k ∈ , thì số trung vị là xk+1.
– Nếu n = 2k, k ∈ , thì số trung vị là
Ý nghĩa: Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường. Vì vậy, khi mẫu số liệu có giá trị bất thường người ta thường dùng trung vị đại diện cho các số liệu thống kê.
c) Tứ phân vị
Tứ phân vị của một mẫu số liệu gồm 3 giá trị, đó là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là Q1, Q2, Q3). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:
– Giá trị tứ phân vị thứ hai, Q2, chính là số trung vị của mẫu.
– Giá trị tứ phân vị thứ nhất, Q1, là số trung vị của nửa số liệu đã sắp xếp bên trái Q2 (không bao gồm Q2 nếu n lẻ).
– Giá trị tứ phân vị thứ ba, Q3, là số trung vị của nửa số liệu đã sắp xếp bên phải Q2 (không bao gồm Q2 nếu n lẻ).
d) Mốt
Mốt là giá trị có tần số lớn nhất của mẫu số liệu. Một mẫu số liệu có thể không có mốt, có một mốt hoặc có nhiều mốt.
Ý nghĩa: Có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.
1.2. Các số đặc trưng đo độ phân tán
a) Khoảng biến thiên
Sắp xếp lại mẫu số liệu là x1, x2, ..., xn theo thứ tự không giảm, ta được dãy
Khoảng biến thiên của một mẫu số liệu, kí hiệu R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là
Ý nghĩa: Khoảng biến thiên dùng để đo mức độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
b) Khoảng tứ phân vị
Khoảng tứ phân vị, kí hiệu , là hiệu giữa tứ phân vị thứ ba Q3 và tứ phân vị thứ nhất Q1, tức là = Q3 - Q1.
Một giá trị của mẫu số liệu được gọi là giá trị bất thường hay giá trị ngoại lệ nếu nó nhỏ hơn Q1 - 1,5 hoặc lớn hơn Q3 + 1,5.
Ý nghĩa: Khoảng tứ phân vị dùng để đo mức độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.
c) Phương sai và độ lệch chuẩn
• Ta có một mẫu số liệu là x1, x2, ..., xn. Cỡ mẫu là n. Số trung bình là
– Phương sai của mẫu số liệu trên, kí hiệu s2, được tính bởi công thức
– Độ lệch chuẩn, kí hiệu s, là căn bậc hai (số học) của phương sai, tức là
• Nếu mẫu số liệu được cho dưới dạng bảng tần số như Bảng 1 thì công thức tính phương sai trở thành
Ý nghĩa: Phương sai hoặc độ lệch chuẩn càng lớn thì số liệu càng phân tán.
2. Các số đặc trưng của mẫu số liệu ghép nhóm
2.1. Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm
a) Số trung bình
Cho mẫu số liệu ghép nhóm như ở Bảng 2.
Nhóm |
Giá trị đại diện |
Tần số |
|
[a1; a2) [a2; a3) ... [am; am+1) |
x1 x2 ... xm |
n1 n2 ... nm |
n = n1 + n2 + ... + nm |
Bảng 2
• Trung điểm xi của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm i là giá trị đại diện của nhóm đó. Chẳng hạn, giá trị đại diện của nhóm [a1; a2) là
• Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu , được tính theo công thức:
Ý nghĩa: Số trung bình cộng của mẫu số liệu ghép nhóm có thể làm đại diện cho vị trí trung tâm của mẫu số liệu đó khi các số liệu trong mẫu ít sai lệch với số trung bình cộng.
b) Trung vị
Cho mẫu số liệu ghép nhóm như ở Bảng 3.
Nhóm |
Tần số |
Tần số tích lũy |
|
[a1; a2) [a2; a3) ... [am; am+1) |
n1 n2 ... nm |
cf1 = n1 cf2 = n1 + n2 ... cfm = n1 + n2 + ... + nm |
n = n1 + n2 + ... + nm |
Bảng 3
Giả sử nhóm k là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng , tức là nhưng . Ta gọi r, d, nk lần lượt là đầu mút trái, độ dài, tần số của nhóm k; cfk-1 là tần số tích lũy của nhóm k - 1.
Trung vị của mẫu số liệu ghép nhóm, kí hiệu Me, được tính theo công thức:
Quy ước: cf0 = 0.
Ý nghĩa: Trung vị của mẫu số liệu có thể dùng để đại diện cho mẫu số liệu đó.
c) Tứ phân vị
Cho mẫu số liệu ghép nhóm như ở Bảng 3.
• Giả sử nhóm p là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng , tức là nhưng . Ta gọi s, h, np lần lượt là đầu mút trái, độ dài, tần số của nhóm p; cfp-1 là tần số tích lũy của nhóm p - 1.
Tứ phân vị thứ nhất Q1 được tính theo công thức
Tứ phân vị thứ hai Q2 bằng trung vị Me.
• Giả sử nhóm q là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng , tức là nhưng . Ta gọi t, l, nq lần lượt là đầu mút trái, độ dài, tần số của nhóm q; cfq-1 là tần số tích lũy của nhóm q - 1.
Tứ phân vị thứ ba Q3 được tính theo công thức
Ý nghĩa: Tứ phân vị Q1, Q2, Q3 của mẫu số liệu chia mẫu số liệu đó thành bốn phần, mỗi phần chứa 25% giá trị.
d) Mốt
Cho mẫu số liệu ghép nhóm như ở Bảng 3.
Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi u, g, ni lần lượt là đầu mút trái, độ dài, tần số của nhóm i; ni-1, ni+1 lần lượt là tần số của nhóm i - 1, nhóm i + 1. Mốt của mẫu số liệu ghép nhóm, kí hiệu M0, được tính theo công thức
Quy ước: n0 = 0; nm+1 = 0.
Ý nghĩa: Mốt của mẫu số liệu ghép nhóm có thể dùng để đo xu thế trung tâm của mẫu số liệu đó.
2.2. Các số đặc trưng đo độ phân tán của mẫu số liệu ghép nhóm
a) Khoảng biến thiên
Cho mẫu số liệu ghép nhóm như ở Bảng 4, trong đó n1 và nm là các số nguyên dương.
Nhóm |
Tần số |
|
[a1; a2) [a2; a3) ... [am; am+1) |
n1 n2 ... nm |
n = n1 + n2 + ... + nm |
Bảng 4
Gọi a1, am+1 lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm m.
Hiệu R = am+1 - a1 được gọi là khoảng biến thiên của mẫu số liệu ghép nhóm đó.
Ý nghĩa:
• Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán cho mẫu số liệu đó. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
• Trong các đại lượng đo mức độ phân tán của mẫu số liệu ghép nhóm, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị là a1 và am+1 của mẫu số liệu nên đại lượng đó dễ bị ảnh hưởng bởi các giá trị bất thường.
b) Khoảng tứ phân vị
Cho mẫu số liệu ghép nhóm như ở Bảng 3. Gọi Q1, Q2, Q3 là tứ phân vị của mẫu số liệu đó. Ta gọi hiệu là khoảng tứ phân vị của mẫu số liệu đó.
Ý nghĩa: Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.
c) Phương sai và độ lệch chuẩn
Cho mẫu số liệu ghép nhóm như ở Bảng 2.
• Gọi là số trung bình cộng của mẫu số liệu đó.
Số được gọi là phương sai của mẫu số liệu đó.
• Căn bậc hai (số học) của phương sai được gọi là độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, nghĩa là
Ý nghĩa:
• Phương sai (độ lệch chuẩn) của mẫu số liệu ghép nhóm được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
• Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.
• Khi hai mẫu số liệu ghép nhóm có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Tính toán các số đặc trưng cho mẫu số liệu không ghép nhóm
1.1. Phương pháp giải
Nắm vững các công thức đã nêu trong phần lý thuyết để xác định: số trung bình, trung vị, tứ phân vị, mốt, khoảng tứ phân vị, khoảng biến thiên, phương sai và độ lệch chuẩn của mẫu số liệu không ghép nhóm.
1.2. Ví dụ
Ví dụ 1. Một cửa hàng bán xe đạp thống kê số xe bán được hằng tháng trong năm 2021 ở bảng sau:
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Số xe |
10 |
8 |
7 |
5 |
8 |
22 |
28 |
25 |
20 |
10 |
9 |
7 |
a) Hãy tính số xe trung bình cửa hàng bán được mồi tháng trong năm 2021.
b) Hãy so sánh hiệu quả kinh doanh trong quý III của cửa hàng với 6 tháng đầu năm 2021.
Hướng dẫn giải
a) Số xe trung bình cửa hàng bán được mỗi tháng trong năm 2021 là:
(10 + 8 + 7 + 5 + 8 + 22 + 28 + 25 + 20 + 10 + 9 + 7) = 13,25 (xe).
b) Số xe trung bình bán được trong 6 tháng đầu năm là:
(10 + 8 + 7 + 5 + 8 + 22) = 10 (xe).
Số xe trung bình bán được trong quý III của năm là:
(28 + 25 + 20) = (xe).
Như vậy hiệu quả kinh doanh của cửa hàng trong quý III cao hơn trong 6 tháng đầu năm.
Ví dụ 2. Bảng sau thống kê số sách mỗi bạn học sinh Tổ 1 và Tổ 2 đã đọc ở thư viện trường trong một tháng:
Tổ 1 |
3 |
1 |
2 |
1 |
2 |
2 |
3 |
25 |
1 |
Tổ 2 |
4 |
5 |
4 |
3 |
3 |
4 |
5 |
4 |
a) Tính các trung vị của số sách các bạn ở Tổ 1 và số sách các bạn ở Tổ 2 đã đọc
b) Sử dụng trung vị, hãy so sánh xem các bạn ở tổ nào đọc nhiều sách ở thư viện hơn.
Hướng dẫn giải
a) Sắp xếp số sách mỗi bạn Tỗ 1 đã đọc theo thứ tự không giảm, ta được dãy: 1; 1; 1; 2; 2; 2; 3; 3; 25.
Vì cỡ mẫu bằng 9 nên trung vị của Tổ 1 là số liệu thứ 5 của dãy trên, tức là Me = 2. Sắp xếp số sách mỗi bạn Tổ 2 đã đọc theo thứ tự không giảm, ta được dãy:
3; 3; 4; 4; 4; 4; 5; 5.
Vì cỡ mẫu bằng 8 nên trung vị của Tổ 2 là trung bình cộng của số liệu thứ 4 và thứ 5 của dãy trên, tức là Me = (4 + 4) = 4.
b) Nếu so sánh theo trung vị thì các bạn Tổ 2 đọc nhiều sách ở thư viện hơn các bạn Tổ 1.
Ví dụ 3. Độ tuổi của 11 cầu thủ ở đội hình xuất phát của một đội bóng đá được ghi lại như sau:
32 20 19 21 28 29 21 22 29 19 29.
Tứ phân vị của mẫu số liệu trên là
A. Q1 = 19, Q2 = 22, Q3 = 32.
B. Q1 = 20, Q2 = 22, Q3 = 28.
C. Q1 = 20, Q2 = 26, Q3 = 29.
D. Q1 = 20, Q2 = 22, Q3 = 29.
Hướng dẫn giải
Sắp xếp mẫu số liệu theo thứ tự tăng dần ta được
19 19 20 21 21 22 28 29 29 29 32.
Vì cỡ mẫu là 11 là số lẻ nên tứ phân vị thứ hai là Q2 = 22.
Tứ phân vị thứ nhất là trung vị của mẫu: 19; 19; 20; 21; 21. Do đó Q1 = 20.
Tứ phân vị thứ ba là trung vị của mẫu: 28; 29; 29; 29; 32. Do đó Q3 = 29.
Vậy tứ phân vị của mẫu số liệu là Q1 = 20, Q2 = 22, Q3 = 29. Chọn D.
Ví dụ 4. Số vụ va chạm giao thông mỗi ngày tại một ngã tư được ghi lại trong bảng tần số sau:
Số vụ va chạm |
0 |
1 |
2 |
3 |
4 |
Số ngày |
12 |
17 |
6 |
4 |
1 |
Tìm mốt của mẫu số liệu trên.
Hướng dẫn giải
Số ngày có 1 vụ va chạm là 17, lớn hơn số ngày có 0, 2, 3, 4 vụ va chạm. Do đó mẫu số liệu trên có mốt là M0 = 1.
Ví dụ 5. Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu: 10; 20; 3; 1; 3; 4; 7; 4; 9.
Hướng dẫn giải
Xét mẫu số liệu đã sắp xếp là: 1; 3; 3; 4; 4; 7; 9; 10; 20.
- Khoảng biến thiên của mẫu số liệu là: R = 20 - 1 = 19.
- Cỡ mẫu là n = 9 là số lẻ nên giá trị tứ phân vị thứ hai là: Q2 = 4.
- Tứ phân vị thứ nhất là trung vị của mẫu: 1; 3; 3; 4. Do đó Q1 = 3.
- Tứ phân vị thứ ba là trung vị của mẫu: 7; 9; 10; 20. Do đó Q3 = 9,5.
- Khoảng tứ phân vị của mẫu là: = 9,5 - 3 = 6,5.
Ví dụ 6. Số liệu thống kê 100 học sinh tham gia kì thi học sinh giỏi toán (thang điểm 20). Kết quả được thống kê trong bảng sau:
Tính độ lệch chuẩn của bảng số liệu thống kê.
Hướng dẫn giải
Điểm số trung bình của các học sinh tham gia thi học sinh giỏi là
Phương sai của số liệu thống kê là
Suy ra độ lệch chuẩn của bảng số liệu thống kê là
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Số lượng đặt bàn của một nhà hàng được cho bởi bảng sau:
Số lượt đặt bàn |
Tần số |
Tần số tích lũy |
[1; 6) |
14 |
14 |
[6; 11) |
30 |
44 |
[11; 16) |
25 |
69 |
[16; 21) |
18 |
87 |
[21; 26) |
5 |
92 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi bảng trên.
A.
B.
C.
D.
Câu 2. Kết quả điều tra mức lương hằng tháng của 9 công nhân của một nhà máy được cho ở mẫu số liệu sau (đơn vị: triệu đồng):
2 9 9 8 10 9 9 11 9.
Giá trị ngoại lệ trong mỗi mẫu số liệu trên là:
A. 11.
B. 9.
C. 2.
D. Không có giá trị ngoại lệ.
Câu 3. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau:
Cỡ áo |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
Tần số (Số áo bán được) |
13 |
45 |
126 |
125 |
110 |
40 |
12 |
Giá trị mốt của bảng phân bố tần số trên bằng
A. 38.
B. 126.
C. 42.
D. 12.
Câu 4. Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) |
[0; 20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Mẫu số liệu ghép nhóm này có mốt là
A. 59.
B. 40.
C. 52.
D. 53.
Câu 5. Trong tuần lễ bảo vệ môi trường, các học sinh khối 11 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 11 ở bảng sau:
Số vỏ chai nhựa |
[11; 15] |
[16; 20] |
[21; 25] |
[26; 30] |
[31; 35] |
Số học sinh |
53 |
82 |
48 |
39 |
18 |
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
A. 19,51.
B. 19,59.
C. 20,2.
D. 18,6.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h).
49 |
42 |
51 |
55 |
45 |
60 |
53 |
55 |
44 |
65 |
52 |
62 |
41 |
44 |
57 |
56 |
68 |
48 |
46 |
53 |
63 |
49 |
54 |
61 |
59 |
57 |
47 |
50 |
60 |
62 |
48 |
52 |
58 |
47 |
60 |
55 |
45 |
47 |
48 |
61 |
Sau khi ghép nhóm mẫu số liệu trên thành sáu nhóm ứng với sáu nửa khoảng:
[40; 45), [45; 50), [50; 55), [55; 60), [60; 65), [65; 70).
thì trung vị của mẫu số liệu ghép nhóm nhận được bằng (km/h) (với là phân số tối giản). Khi đó giá trị của a bằng bao nhiêu?
Điền đáp án |
Câu 17. Cho dãy số liệu thống kê: x; 21; 22; 23; 24; y. Biết dãy trên đã được sắp xếp tăng dần, trung bình cộng bằng 22,5 và khoảng biến thiên của mẫu số liệu bằng 5. Tính x.y.
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
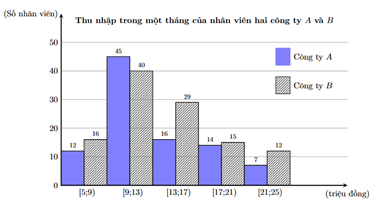
Câu 19. Thống kê lại thu nhập trong một tháng của nhân viên hai công ty A và B (đơn vị: triệu đồng) được thể hiện trong biểu đồ dưới đây.
a) Có 14 nhân viên của công ty A thu nhập từ 17 triệu đồng đến 21 triệu đồng trong một tháng.
b) Thu nhập trung bình mỗi tháng của nhân viên công ty A cao hơn nhân viên công ty B.
c) Nếu so sánh về phương sai thì thu nhập mỗi tháng của nhân viên công ty A ít phân tán hơn nhân viên công ty B.
d) Nếu so sánh về khoảng tứ phân vị thì thu nhập trung bình mỗi tháng của công ty B đồng đều hơn công ty A.
................................
................................
................................
I. LÝ THUYẾT CẦN NHỚ
1. Quy tắc đếm
1.1. Quy tắc cộng
Một công việc được hoàn thành bởi một trong hai hành động:
– Hành động thứ nhất có m cách thực hiện;
– Hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một).
→ Khi đó số cách hoàn thành công việc là: m + n cách.
* Chú ý: Quy tắc cộng có thể mở rộng cho một công việc được hoàn thành bởi một trong k hành động (, k > 2).
Nếu A và B là các tập hợp hữu hạn không giao nhau thì: n (A B) = n (A) + n (B).
1.2. Quy tắc nhân
Một công việc phải hoàn qua hai công đoạn liên tiếp nhau:
– Công đoạn một có m cách thực hiện;
– Với mỗi cách thực hiện công đoạn một, có n cách thực hiện công đoạn hai.
→ Khi đó số cách hoàn thành công việc là: m.n cách.
* Chú ý: Quy tắc nhân có thể mở rộng cho một công việc được hoàn thành bởi k hành động liên tiếp (, k > 2).
2. Hoán vị, chỉnh hợp, tổ hợp
2.1. Hoán vị
Cho tập hợp A gồm n phần tử (). Mỗi kết quả của sự sắp xếp n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
Số các hoán vị của n phần tử là:
2.2. Chỉnh hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với . Mỗi kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Kí hiệu là số các chỉnh hợp chập k của n phần tử ().
Số các chỉnh hợp chập k của n phần tử là: hay
2.3. Tổ hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với . Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của tập hợp A được gọi là một tổ hợp chập k của n phần tử đó.
Kí hiệu là số các tổ hợp chập k của n phần tử
Số các tổ hợp chập k của n phần tử với là:
Quy ước: 0! = 1, . Khi đó, ta có:
3. Xác suất
3.1. Các bước tính xác suất (theo định nghĩa xác suất cổ điển)
Bước 1. Xác định không gian mẫu rồi tính số phần tử của , tức là đếm số kết quả có thể của phép thử T.
Bước 2. Xác định tập con A mô tả biến cố A rồi tính số phần tử của A, tức là đếm số kết quả thuận loại cho A.
Bước 3. Lấy kết quả của bước 2 chia cho
Nhận xét: Việc tính số kết quả có thể (bước 1) thường dễ dàng hơn hiều so với việc tính số kết quả thuận lợi cho A (bước 2). Để giải quyết tốt các bài toán xác suất ta cần nắm chắc phần tổ hợp trước.
Từ định nghĩa cổ điển về xác suất ta suy ra:
* Lưu ý: Các kí hiệu n (), n (A) được hiểu tương đương với ||, |A| là số phần tử của không gian mẫu và của tập hợp thuận lợi cho biến cố A.
Bảng đọc ngôn ngữ biến cố
Kí hiệu |
Ngôn ngữ biến cố |
A là biến cố |
|
A = |
A là biến cố không |
A = |
A là biến cố chắc chắn |
C = A B |
C là biến cố hợp: “A hoặc B” |
C = A B |
C là biến cố giao: “A và B” |
A B = |
A và B xung khắc |
B = |
A và B đối nhau |
3.2. Các phương pháp tính xác suất
• Tính xác suất bằng định nghĩa: Công thức tính xác suất của biến cố A:
• Quy tắc cộng xác suất:
* Nếu hai biến cố A, B xung khắc nhau thì P (A B) = P (A) + P (B).
* Nếu các biến cố A1, A2, A3, ..., Ak xung khắc nhau thì
= P (A1) + P (A2) + ... + P (Ak).
Vì và nên theo công thức cộng xác suất thì
• Công thức tính xác suất biến cố đối:
Xác suất của biến cố của biến cố A là: P () = 1 - P (A).
• Quy tắc nhân xác suất:
* Nếu A và B là hai biến cố độc lập thì P (AB) = P (A).P (B).
* Một cách tổng quát, nếu k biến cố A1, A2, A3, ..., Ak là độc lập thì
P (A1A2A3 ... Ak) = P (A1).P (A2). ... .P (Ak).
* Lưu ý: Nếu A và B độc lập thì A và độc lập, B và độc lập, và độc lập. Do đó nếu A và B độc lập thì ta còn có các đẳng thức:
P (A) = P (A).P ()
P (B) = P ().P (B)
P () = P ().P ()
Nếu một trong các đẳng thức trên bị vi phạm thì hai biến cố A và B không độc lập với nhau.
4. Xác suất có điều kiện
Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P (A| B). Nếu P (B) > 0 thì
Từ định nghĩa của xác suất có điều kiện, suy ra: nếu P (B) > 0 thì = P (B).P (A| B).
* Chú ý:
• Công thức nhân xác suất: Với hai biến cố A và B bất kì thì
= P (A).P (B| A) = P (B).P (A| B).
• Cho hai biến cố A và B với P (B) > 0. Khi đó, ta có:
• Cho hai biến cố A và B với 0 < P (A) < 1, 0 < P (B) < 1. Khi đó, A và B là hai biến cố độc lập khi và chỉ khi P (A) = P (A| B) = P (A| ) và P (B) = P (B| A) = P (B| ) .
5. Công thức xác suất toàn phần. Công thức Bayes
5.1. Công thức xác suất toàn phần
Cho hai biến cố A và B với 0 < P (B) < 1, ta có công thức xác suất toàn phần:
= P (B).P (A| B) +
5.2. Công thức Bayes
Cho hai biến cố A và B với P (A) > 0, P (B) > 0 ta có:
Nhận xét: Với P (A) > 0, 0 < P (B) < 1 thì ta có
= P (B).P (A| B) +
Nên công thức Bayes còn có dạng
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Sử dụng định nghĩa để tính xác suất
1.1. Phương pháp giải
Bước 1. Xác định biến cố của các xác suất, có thể gọi tên các biến cố A; B; C; D để biểu diễn.
Bước 2. Tìm mối quan hệ giữa các biến cố vừa đặt tên, biểu diễn biến cố trung gian và quan trọng nhất là biến cố đề bài đang yêu cầu tính xác suất thông qua các biến cố ở bước 1.
Bước 3. Sử dụng các mối quan hệ vừa xác định ở bước 2 để chọn công thức cộng hay công thức nhân phù hợp.
1.2. Ví dụ
Ví dụ 1. Một con xúc xắc cân đối đồng chất được gieo 5 lần. Xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba:
A.
B.
C.
D.
Hướng dẫn giải
Số phần tử không gian mẫu:
Bộ kết quả của 3 lần gieo thỏa yêu cầu là: (1; 1; 2); (1; 2; 3); (2; 1; 3); (1; 3; 4); (3; 1; 4); (2; 2; 4); (1; 4; 5); (4; 1; 5); (2; 3; 5); (3; 2; 5); (1; 5; 6); (5; 1; 6); (2; 4; 6); (4; 2; 6); (3; 3; 6).
Nên n (A) = 15.6.6 Chọn B.
Ví dụ 2. Có 2 hộp bút chì màu. Hộp thứ nhất có có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ hai có có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Xác suất để có 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh là:
A.
B.
C.
D.
Hướng dẫn giải
Gọi A là biến cố: “có 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh”.
Không gian mẫu:
Số cách chọn được 1 bút đỏ ở hộp 1,1 bút xanh ở hộp 2 là:
Số cách chọn được 1 bút đỏ ở hộp 2,1 bút xanh ở hộp 1 là:
. Chọn A.
Ví dụ 3. Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, một toa có 1 người, 2 toa còn lại không có ai.
A.
B.
C.
D.
Hướng dẫn giải
Không gian mẫu:
Chọn 1 toa để xếp 3 người có 4 cách chọn; xếp 3 người vào toa đó có: cách.
Chọn 1 toa để xếp 1 người có 3 cách chọn.
Tổng số cách chọn thỏa mãn là: n (A) = 4.4.3 = 48 cách.
Vậy xác suất là: Chọn D.
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Một người chọn ngẫu nhiên 2 chiếc giày từ 5 đôi giày cỡ khác nhau. Tính xác suất để 2 chiếc giày được chọn tạo thành một đôi.
A.
B.
C.
D.
Câu 2. Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, một toa có 1 người, 2 toa còn lại không có ai.
A.
B.
C.
D.
Câu 3. Có hai hộp, mỗi hộp chứa 5 tấm thẻ đánh số từ 1 đến 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Tính xác suất để 2 thẻ rút ra đều ghi số chẵn.
A.
B.
C.
D.
Câu 4. Một hộp có 4 quả cầu xanh, 3 quả cầu đỏ và 2 quả cầu vàng. Chọn ngẫu nhiên 2 quả cầu. Tính xác suất để chọn được 2 quả cầu khác màu.
A.
B.
C.
D.
Câu 5. Gọi S là tập các số tự nhiên có 4 chữ số khác nhau được tạo từ tập E = {1; 2; 3; 4; 5}. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chẵn.
A.
B.
C.
D.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Tại bệnh viện bỏng Hà Nội, có 70% bệnh nhân bị bỏng do nhiệt và 30% bệnh nhân bị bỏng là do hóa chất. Biết rằng tỷ lệ biến chứng do bỏng nhiệt là 30% còn bỏng do hóa chất có tỷ lệ biến chứng là 50%. Tính xác suất biến chứng chung của toàn bệnh nhân bỏng.
Điền đáp án |
Câu 17. Cho tập hợp A = {1; 2; 3; ...; 10}. Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Trường THPT X có 8 giáo viên Toán gồm có 3 nữ và 5 nam, 4 giáo viên Vật lý nam.
a) Có 3 cách chọn một giáo viên nữ.
b) Có 1 320 cách lập một đoàn công tác gồm 3 giáo viên trong đó có 1 trưởng đoàn, 1 phó đoàn và 1 thành viên.
c) Có 95 040 cách lập một đoàn công tác gồm 5 giáo viên trong đó có 1 trưởng đoàn, 1 phó đoàn và 3 thành viên.
d) Có 80 cách chọn ra một đoàn công tác gồm 3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn.
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGNL HSA) Chuyên đề: Góc, khoảng cách trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Thể tích của một số hình khối
- (Ôn thi ĐGNL HSA) Chuyên đề: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
- (Ôn thi ĐGNL HSA) Chuyên đề: Nguyên hàm - Tích phân
- (Ôn thi ĐGNL HSA) Chuyên đề: Vectơ và phương pháp tọa độ trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Một số câu hỏi trích trong các đề thi tham khảo
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều


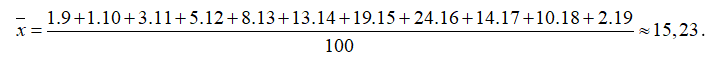
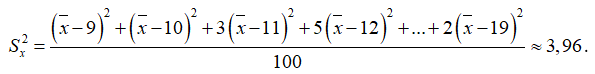



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

