(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Chuyên đề Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
(Ôn thi ĐGNL, ĐGTD) Tính đơn điệu của hàm số
I. LÝ THUYẾT CẦN NHỚ
1. Tính đơn điệu của hàm số
1.1. Định nghĩa
Giả sử K là một khoảng, một đoạn hoặc nửa khoảng và y = f(x) là hàm số xác định trên K. Ta nói:
• Hàm số y = f(x) được gọi là đồng biến trên K nếu thì f(x1) < f(x2).
• Hàm số y = f(x) được gọi là nghịch biến trên K nếu thì f(x1) > f(x2).
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên tập
1.2. Định lí 1
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng K thì
b) Nếu hàm số nghịch biến trên khoảng K thì
1.3. Định lí 2
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu thì hàm số f đồng biến trên K.
b) Nếu thì hàm số f nghịch biến trên K.
c) Nếu thì hàm số f không đổi trên K.
* Lưu ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có thêm giả thuyết “Hàm số liên tục trên đoạn hoặc nửa khoảng đó”.
Chẳng hạn: Nếu hàm số f liên tục trên đoạn [a; b] và f' (x) > 0, thì hàm số f đồng biến trên đoạn [a; b].
Ta thường biểu diễn qua bảng biến thiên như sau:
1.4. Định lí 3. (Mở rộng của định lí 2)
Giả sử hàm số y = f(x) có đạo hàm trên
• Nếu và f' (x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số y = f(x) đồng biến trên K.
• Nếu và f' (x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số y = f(x) nghịch biến trên K.
• Nếu thì hàm số y = f(x) không đổi trên K.
2. Cực trị của hàm số
2.1. Định nghĩa
Cho hàm số y = f(x) liên tục trên tập , trong đó K là một khoảng, một đoạn hoặc nửa khoảng và
• Điểm x0 gọi là điểm cực đại của hàm số y = f(x) nếu tồn tại một khoảng (a; b) sao cho
và
Khi đó f(x0) gọi là giá trị cực đại (hay cực đại) của hàm số y = f(x).
• Điểm x0 gọi là điểm cực tiểu của hàm số y = f(x) nếu tồn tại một khoảng (a; b) sao cho
và
Khi đó f(x0) gọi là giá trị cực tiểu (hay cực tiểu) của hàm số y = f(x).
Điểm cực đại và điểm cực tiểu của hàm số được gọi chung là điểm cực trị của hàm số đó; giá trị cực đại (cực đại) và giá trị cực tiểu (cực tiểu) của hàm số được gọi chung là giá trị cực trị (hay cực trị) của hàm số đó.
Nếu x0 là điểm cực trị của hàm số y = f(x) thì điểm M (x0; f(x0)) được gọi là điểm cực trị của đồ thị hàm số y = f(x).
2.2. Định lí
Cho hàm số y = f(x) liên tục trên khoảng (a, b) chứa điểm x0 và có đạo hàm trên các khoảng (a; x0) và (x0; b). Khi đó:
• Nếu f' (x) < 0 với mọi và thì hàm số y = f(x) đạt cực tiểu tại điểm x0.
• Nếu f' (x) > 0 với mọi và thì hàm số y = f(x) đạt cực đại tại điểm x0.
2.3. Các bước tìm điểm cực trị của hàm số f (x)
Bước 1. Tìm tập xác định của hàm số f (x).
Bước 2. Tính đạo hàm f' (x). Tìm các điểm xi (i = 1, 2, ... , n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên của hàm số f (x) hoặc bảng xét dấu f '(x).
Bước 4. Kết luận về các điểm cực trị của hàm số.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán. Tìm khoảng đơn điệu của hàm số cho trước
1.1. Phương pháp giải
Để tìm khoảng đơn điệu của hàm số cho trước, ta thực hiện như sau:
Bước 1. Tìm tập xác định của hàm số y = f (x).
Bước 2.Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, ... , n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên của f (x) hoặc bảng xét dấu của f'(x).
Bước 4. Kết luận khoảng đồng biến, nghịch biến của hàm số.
* Lưu ý: Để phù hợp thi trắc nghiệm các em có thể chi cần xét dấu y' là có thể kết luận được tính đơn điệu của hàm số mà không nhất thiết phải vẽ bảng biến thiên.
1.2. Ví dụ
Ví dụ 1. Cho hàm số y = x4 - 2x2. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (−∞; -2)
B. Hàm số đồng biến trên khoảng (−1; 1)
C. Hàm số nghịch biến trên khoảng (−1; 1)
D. Hàm số nghịch biến trên khoảng (−∞; -2)
Hướng dẫn giải
TXĐ:
Ta có y' = 4x3 - 4x; y' = 0 4x3 - 4x = 0
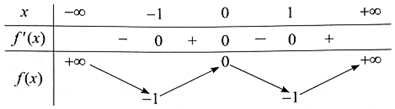
Bảng biến thiên:
Từ bảng biến thiên suy ra hàm số đồng biến trên các khoảng (-1; 0), (1; +∞); hàm số nghịch biến trên các khoảng (-∞; -1), (0; 1). Vậy hàm số nghịch biến trên khoảng (-∞; -2). Chọn D.
Ví dụ 2. Hàm số y = -x3 + 3x2 - 2 đồng biến trên khoảng
A. (0; 2).
B. (-∞; 0).
C. (1; 4).
D. (4; +∞).
Hướng dẫn giải
Tập xác định
Ta có: y' = -3x2 + 6x; y' = 0
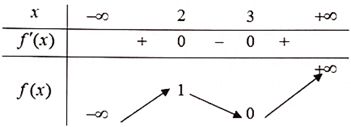
Bảng xét dấu của y' như sau:
Nhìn vào bảng xét dấu của y' ta thấy hàm số y = -x3 + 3x2 - 2 đồng biến trên khoảng (0; 2).
Vậy hàm số y = -x3 + 3x2 - 2 đồng biến trên khoảng (0; 2). Chọn A.
Ví dụ 3. Hàm số nghịch biến trên khoảng nào trong các khoảng sau đây?
A. (1010; 2018).
B. (2018; +∞).
C. (0; 1009).
D. (1; 2018).
Hướng dẫn giải
TXD: D = [0; 2018]
Ta có
, suy ra hàm số nghịch biến trên khoảng (1009; 2018), suy ra hàm số nghịch biến trên khoảng (1010; 2018). Chọn A.
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Cho hàm số y = x3 - 2x2 + x + 1. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên
B. Hàm số nghịch biến trên
C. Hàm số đồng biến trên
D. Hàm số nghịch biến trên
Câu 2. Cho hàm số y = x4 - 2x2. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (−∞; -2).
B. Hàm số đồng biến trên khoảng (−∞; -2).
C. Hàm số đồng biến trên (−1; 1).
D. Hàm số nghịch biến trên (−1; 1).
Câu 3. Trên khoảng nào sau đây, hàm số đồng biến?
A. (1; +∞)
B. (1; 2).
C. (0; 1).
D. (−∞; 1)
Câu 4. Cho hàm số Khẳng định nào dưới đây là đúng?
A. Hàm số đồng biến trên \ {2}.
B. Hàm số nghịch biến trên (−2; +∞)
C. Hàm số nghịch biến trên (−∞; 2) và (2; +∞)
D. Hàm số nghịch biến trên .
Câu 5. Quan sát đồ thị của hàm y = f(x) ở hình bên và chọn mệnh đề sai.
A. Hàm số nghịch biến trên khoảng (3; +∞).
B. Hàm số đồng biến trên khoảng (−1; 3).
C. Hàm số nghịch biến trên khoảng (−∞; -1).
D. Hàm số đồng biến trên khoảng (0; 2).
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 21. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = (m2 - m) x3 + 2mx2 + 3x - 2 đồng biến trên khoảng (−∞; +∞)?
Điền đáp án |
Câu 22. Cho hàm số f (x) có đạo hàm f' (x) = x2 (x - 1)(m - x2 - 3). Có bao nhiêu số nguyên âm m để hàm số y = f (x2) đồng biến trên khoảng (1; +∞)?
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 24. Cho hàm số y = x3 + (m + 1) x2 + (m2 + 2m) x - 3, với m là tham số.
a) Tập xác định của hàm số là
b) Phương trình y' = 0 có hai nghiệm phân biệt là x1 = -m và x = -m - 2.
c) Không tồn tại giá trị của tham số m để hàm số đồng biến trên
d) Hàm số nghịch biến trên (-1; 1) khi và chỉ khi
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Giá trị lớn nhất - Giá trị nhỏ nhất
I. LÝ THUYẾT CẦN NHỚ
1. Định nghĩa
Cho hàm số y = f(x) xác định trên tập hợp D.
• Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M. Kí hiệu
• Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) ≥ m với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = m. Kí hiệu
* Lưu ý:
+ Nếu chỉ có điều kiện f(x) ≤ M với mọi x ∈ D thì ta chưa thể suy ra
+ Nếu chỉ có điều kiện f(x) ≥ m với mọi x ∈ D thì ta chưa thể suy ra
2. Các phương pháp tìm GTLN, GTNN của hàm số
• Phương pháp chung: Để tìm GTLN, GTNN của hàm số y = f(x) trên D, ta tính y', tìm các điểm mà tại đó đạo hàm triệt tiêu hoặc không tồn tại và lập bảng biến thiên. Từ bảng biến thiên ta suy ta GTLN, GTNN của hàm số.
• Giả sử hàm số y = f(x) liên tục trên đoạn [a; b] và có đạo hàm trên khoảng (a; b), có thể trừ một số hữu hạn điểm. Nếu f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc khoảng (a; b) thì ta có quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b] như sau:
Bước 1. Tìm các điểm x1, x2, ... , xn thuộc khoảng (a; b) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 2. Tính f(a), f(x1), f(x2), ..., f(xn), f(b).
Bước 3. So sánh các giá trị tìm được ở Bước 2. Tìm số lớn nhất M và số nhỏ nhất m.
Khi đó:
* Lưu ý:
+ Nếu y = f(x) đồng biến trên [a; b] thì và
+ Nếu y = f(x) nghịch biến trên [a; b] thì và
• Nếu hàm số y = f(x) tuần hoàn trên chu kỳ T, để tìm GTLN, GTNN của nó trên D ta chỉ cần tìm GTLN, GTNN trên một đoạn thuộc D có độ dài bằng T.
• Cho hàm số y = f(x) xác định trên D. Khi đặt ẩn phụ t = u (x), ta tìm được t ∈ E với , ta có y = g (t) thì Max, Min của hàm f trên D chính là Max, Min của hàm y = g (t) trên E.
• Khi bài toán yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất mà không nói trên tập nào thì ta hiểu là tìm GTLN, GTNN trên tập xác định của hàm số.
• Ngoài phương pháp khảo sát để tìm Max, Min ta có thể dùng phương pháp miền giá trị hoặc bất đẳng thức hoặc Casio để tìm Max, Min.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị, bảng biến thiên
1.1. Phương pháp giải
Dựa vào định nghĩa (xem phần lý thuyết).
1.2. Ví dụ
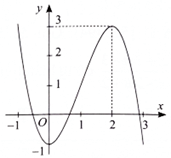
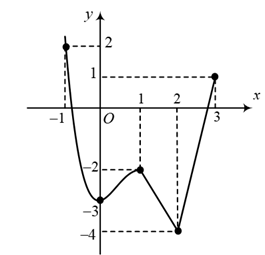
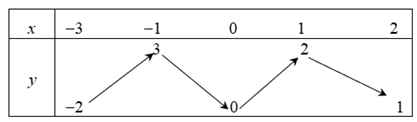
Ví dụ 1. Cho hàm số y = f(x) liên tục trên đoạn [-1; 3] và có đồ thị như hình vẽ.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [-1; 3]. Khi đó, tổng M + m bằng
A. -6.
B. -2.
C. -5.
D. 2.
Hướng dẫn giải
Theo đồ thị, ta có: M = 2 và m = -4 M + m = -2. Chọn B.
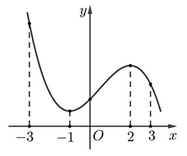
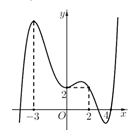
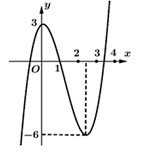
Ví dụ 2. Cho hàm số f(x) = ax3 + bx2 + cx + d có đồ thị như hình vẽ:
Giá trị lớn nhất của hàm số đã cho trên đoạn [-3; 3] bằng
A. f(2).
B. f(-1).
C. f(-3).
D. f(3).
Hướng dẫn giải
Dựa vào đồ thị hàm số đã cho ta thấy hàm số đạt giá trị lớn nhất trên đoạn [-3; 3] bằng f(-3). Chọn C.
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
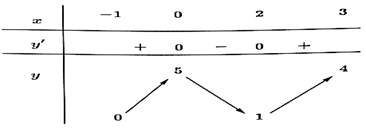
Câu 1. Hàm số y = f(x) liên tục và có bảng biến thiên trên đoạn [-1; 3] cho trong hình dưới. Gọi M là giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1; 3]. Tìm mệnh đề đúng.
A. M = f(-1).
B. M = f(3).
C. M = f(2).
D. M = f(0).
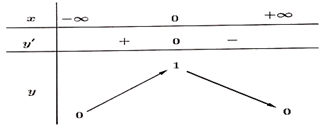
Câu 2. Hàm số có bảng biến thiên như hình vẽ. Xét trên tập xác định của hàm số, hãy chọn khẳng định đúng.
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0.
D. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
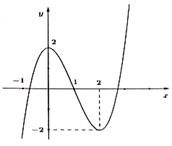
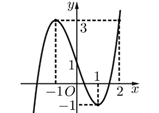
Câu 3. Cho hàm số y = f(x) có đồ thị như hình bên. Khẳng định nào dưới đây là khẳng định sai?
A. Hàm số có hai điểm cực trị.
B. Đồ thị hàm số có hai điểm cực trị (0; 2) và (2; -2).
C. Hàm số đồng biến trên (−∞; 0) và (2; +∞).
D. Hàm số có giá trị lớn nhất là 2 và giá trị nhỏ nhất là −2.
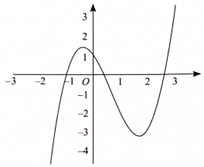
Câu 4. Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây.
Giá trị lớn nhất của hàm số trên [-3; 4] bằng:
A. f(2).
B. f(-3).
C. f(4).
D. f(0).
Câu 5. Cho hàm số y = f(x) liên tục trên đoạn [-3; 2] và có bảng biến thiên như hình vẽ dưới.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-3; 2].
Tính M + m.
A. -1.
B. 1.
C. 3.
D. 5.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Cho hàm số y = x3 - 3mx2 + 3 (m2 - 1) x + 2020. Có tất cả bao nhiêu giá trị nguyên của m sao cho hàm số có giá trị nhỏ nhất trên khoảng (0; +∞)?
Điền đáp án |
Câu 17. Gọi S là tập hợp tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số y = |x4 - 14x2 + 48x + m - 30| trên đoạn [0; 2] không vượt quá 30. Tổng giá trị các phần tử của tập hợp S bằng bao nhiêu?
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Cho hàm số f(x) = x3 - 3x + m, với m là tham số.
a) Khi m = 0 thì hàm số đồng biến trên khoảng (-1; 1).
b) Khi m = 0 thì hàm số có hai điểm cực trị.
c) Giá trị nhỏ nhất của hàm số trên đoạn [0; 2] bằng m - 2.
d) Gọi S là tập tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = |f(x)| trên đoạn [0; 2] bằng 3. Khi đó S có một phần tử.
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Tiệm cận của đồ thị hàm số
I. LÝ THUYẾT CẦN NHỚ
1. Đường tiệm cận ngang
Định nghĩa: Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số f(x) nếu:
hoặc
Đường thẳng y = m là tiệm cận ngang của đồ thị hàm số y = f(x) được minh hoạ như hình vẽ dưới đây.
Nhận xét: Như vậy để tìm tiệm cận ngang của đồ thị hàm số ta đi tính giới hạn của hàm số đó tại vô cực.
* Lưu ý:
- Việc tính giới hạn hàm số tại vô cực có thể thực hiện bằng máy tính Casio với lệnh CALC (lệnh tính giá trị biểu thức).
+ Nếu CALC: x = 105.
+ Nếu CALC: x = -105.
- Đọc kết quả giới hạn trên Casio:
2. Đường tiệm cận đứng
Định nghĩa: Đường thẳng x = a gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
Đường thẳng x = a là tiệm cận đứng của đồ thị hàm số y = f(x) được minh hoạ như hình vẽ dưới đây.
* Lưu ý:
- Điều kiện cần để x = x0 là tiệm cận đứng là x0 phải là nghiệm của mẫu số (tại x0 hàm số không xác định) (trừ một số trường hợp loại hàm số khác như: Hàm số logarit).
- Việc tính giới hạn của hàm số tại có thể thực hiện bằng Casio với lệnh CALC (Lệnh tính giá trị biểu thức).
+ Nếu CALC: x = x0 - 10-5.
+ Nếu CALC: x = x + 10-5.
- Đặc biệt đối với hàm số bậc nhất trên bậc nhất thì đồ thị hàm số luôn có 2 đường tiệm cận gồm 1 tiệm cận đứng , và 1 tiệm cận ngang
3. Đường tiệm cận xiên
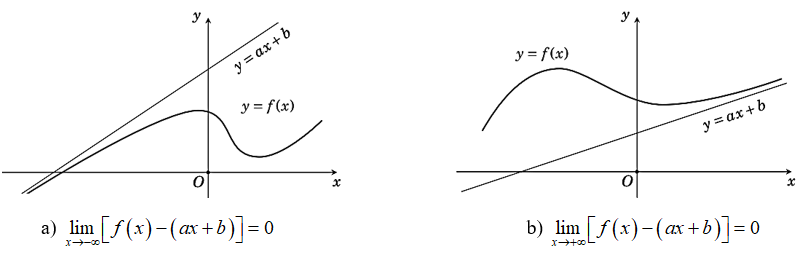
Định nghĩa: Đường thẳng y = ax + b (a ≠ 0) gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu:
hoặc
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y = f(x) được minh hoạ như hình bên dưới:
* Lưu ý: Đối với hàm số phân thức ta có thể chia đa thức để biến đổi về dạng
với e ≠ 0.
Suy ra y = a'x + b' là đường tiệm cận xiên của đồ thị hàm số.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Tìm tiệm cận của đồ thị đã tường minh
1.1. Phương pháp giải
Cho hàm số y = f(x). Để tìm các đường tiệm cận của đồ thị hàm số thì ta làm như sau:
• Các bước tìm đường tiệm cận ngang:
Bước 1: Tính giới hạn và
Bước 2: Xem ở “vị trí” nào ra kết quả hữu hạn thì ta kết luận có tiệm cận ngang ở “vị trí” đó.
• Các bước tìm đường tiệm cận đứng:
Bước 1: Tìm nghiệm của mẫu, giả sử nghiệm đó là x = x0.
Bước 2: Tính giới hạn một bên tại x = x0. Nếu xảy ra hoặc thì ta kết luận x = x0 là đường tiệm cận đứng.
• Tìm đường tiệm cận xiên: Có thể tìm hệ số a, b trong phương trình của đường tiệm cận xiên y = ax + b theo công thức sau: hoặc
1.2. Ví dụ
Ví dụ 1. Tiệm cận ngang của đồ thị hàm số là đường thẳng
A. x = 1.
B. y = 2.
C. x = 0.
D. y = 0.
Hướng dẫn giải
Ta có
Vậy đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. Chọn D.
Ví dụ 2. Đồ thị hàm số có đường tiệm cận đứng là
A.
B.
C. x = 2.
D.
Hướng dẫn giải
Ta có 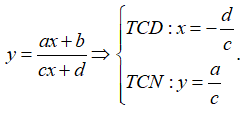
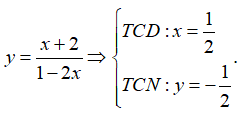
Ví dụ 3. Số tiệm cận đứng của đồ thị hàm số là
A. 1.
B. 2.
C. 0.
D. 3.
Hướng dẫn giải
Tập xác định của hàm số: D = [-9; +∞) \ {0; -1}.
Ta có và
⇒ TCĐ: x = -1.
⇒ x = 0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng. Chọn A.
Ví dụ 4. Tìm đường tiệm cận xiên của đồ thị hàm số
A. y = 2x - 5.
B. y = x - 2.
C. y = x + 5.
D. y = x - 5.
Hướng dẫn giải
Ta có:
;
Vậy đường thẳng y = x + 5 là đường tiệm cận xiên của đồ thị hàm số đã cho khi
Tương tự do và nên đường thẳng y = x + 5 là đường tiệm cận xiên của đồ thị hàm số đã cho khi . Chọn C.
Ví dụ 5. Cho hàm số . Tiệm cận xiên của đồ thì hàm số là đường thẳng:
A. y = 2x - 1.
B. y = 2x + 1.
C. y = 2x - 3.
D. y = 2x + 3.
Hướng dẫn giải
Chia tử thức cho mẫu thức ta được 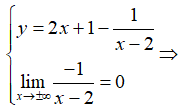
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Cho hàm số y = f(x) có và Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = -1.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1.
Câu 2. Tiệm cận đứng của đồ thị hàm số là
A. x = -1.
B. x = 1.
C. x = -3.
D. x = 3.
Câu 3. Tiệm cận ngang của đồ thị hàm số là
A.
B. y = 4.
C. y = 1.
D. y = -1.
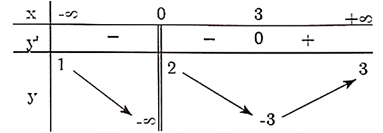
Câu 4. Cho hàm số y = f(x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 2.
B. 3.
C. 4.
D. 1.
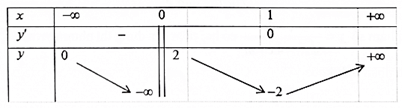
Câu 5. Cho hàm số f(x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 1.
B. 2.
C. 4.
D. 3.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Cho hàm số , m là tham số thực. Có bao nhiêu giá trị của m để đường tiệm cận xiên của đồ thị hàm số đã cho tạo với hai trục tọa độ một tam giác có diện tích bằng
Điền đáp án |
Câu 17. Gọi S là tập các giá trị nguyên của m sao cho đồ thị hàm số có bốn đường tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang). Tính số phần tử của tập S.
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
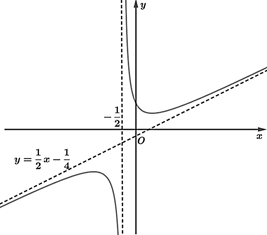
Câu 19. Cho hàm số (mn ≠ 0) có đồ thị (C) như hình vẽ:
a)
b)
c) m + n = 3.
d)
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Tương giao của đồ thị hàm số
I. LÝ THUYẾT CẦN NHỚ
1. Tọa độ giao điểm của hai đồ thị hàm số
Cho 2 hàm số y = f(x) và y = g(x) có đồ thị lần lượt là (C) và (C'):
+ Lập phương trình hoành độ giao điểm của (C) và (C') là f(x) = g(x) (*).
+ Giải phương trình tìm x thay vào f(x) hoặc g(x) để suy ra y và tọa độ giao điểm.
+ Số nghiệm của phương trình (*) là số giao điểm của (C) và (C').
2. Tương giao của đồ thị hàm bậc ba chứa tham số m
Phương pháp 1: Bảng biến thiên (Phương pháp đồ thị)
• Lập phương trình hoành độ giao điểm dạng F (x, m) = 0 (phương trình ẩn x tham số m).
• Cô lập m đưa phương trình về dạng m = f(x).
• Lập bảng biến thiên cho hàm số y = f(x).
• Dựa và giả thiết và bảng biến thiên từ đó suy ra m.
Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi m độc lập với x.
Phương pháp 2: Nhẩm nghiệm – tam thức bậc hai.
• Lập phương trình hoành độ giao điểm F (x, m) = 0.
• Nhẩm nghiệm: (Khử tham số). Giả sử x = x0 là 1 nghiệm của phương trình.
• Phân tích: F (x, m) = 0 (x - x0). g(x) = 0 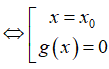
• Dựa vào yêu cầu bài toán đi xử lý phương trình bậc hai g(x) = 0.
Phương pháp 3: Cực trị
Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.
Quy tắc:
Lập phương trình hoành độ giao điểm F (x, m) = 0 (1). Xét hàm số y = F (x, m).
+) Để (1) có đúng 1 nghiệm thì đồ thị y = F (x, m) cắt trục hoành tại đúng 1 điểm. (2TH)
- Hoặc hàm số luôn đơn điệu trên hàm số không có cực trị y' = 0 hoặc vô nghiệm hoặc có nghiệm kép
- Hoặc hàm số có CĐ, CT và
+) Để (1) có đúng 3 nghiệm thì đồ thị y = F (x, m) cắt trục hoành tại 3 điểm phân biệt Hàm số có cực đại, cực tiểu và
+) Để (1) có đúng 2 nghiệm thì đồ thị y = F (x, m) cắt trục hoành tại 2 điểm phân biệt Hàm số có cực đại, cực tiểu và
Bài toán: Tìm m để đồ thị hàm bậc 3 cắt trục hoành tại 3 điểm lập thành 1 cấp số cộng.
Định lí Vi-et:
Cho bậc hai: Cho phương trình ax2 + bx + c = 0 có 2 nghiệm x1, x2 thì ta có: ,
Cho bậc ba: Cho phương trình ax3 + bx2 + cx + d = 0 có 3 nghiệm x1, x2, x3 thì ta có:
x1 + x2 + x3 = , x1x2+ x2x3 + x3x1 = , x1x2x3
Tính chất của cấp số cộng:
Cho 3 số a, b, c theo thứ tự đó lập thành 1 cấp số cộng thì: a + c = 2b.
Phương pháp giải toán:
Điều kiện cần: là 1 nghiệm của phương trình. Từ đó thay vào phương trình để tìm m.
Điều kiện đủ: Thay m tìm được vào phương trình và kiểm tra.
3. Tương giao của hàm số phân thức
Phương pháp:
Cho hàm số và đường thẳng d: y = px + q.
Phương trình hoành độ giao điểm của (C) và d:
F (x, m) = 0 (1) (phương trình bậc hai ẩn x tham số m).
* Các câu hỏi thường gặp:
(1) Tìm m để d cắt (C) tại 2 điểm phân biệt (1) có 2 nghiệm phân biệt khác
(2) Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C) (1) có 2 nghiệm phân biệt x1, x2 và thỏa mãn:
(3) Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C) (1) có 2 nghiệm phân biệt x1, x2 và thỏa mãn
(4) Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc 2 nhánh của (C) (1) có 2 nghiệm phân biệt x1, x2 và thỏa mãn
(5) Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước:
• Đoạn thẳng AB = k.
• Tam giác ABC vuông.
• Tam giác ABC có diện tích S0.
Quy tắc:
• Tìm điều kiện tồn tại A, B → (1) có 2 nghiệm phân biệt.
• Xác định tọa độ của A và B (chú ý Vi-et).
• Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m.
* Lưu ý: Công thức khoảng cách:
A (xA; yA), B (xB; yB) : AB =
4. Tương giao của hàm số bậc bốn
Nghiệm của phương trình trùng phương: ax4 + bx2 + c = 0 (1).
a) Nhẩm nghiệm
- Nhẩm nghiệm: Giả sử x = x0 là một nghiệm của phương trình.
- Khi đó ta phân tích: f(x, m) = (x2 - ) g(x) = 0
- Dựa vào giả thiết xử lý phương trình bậc hai g(x) = 0.
b) Ẩn phụ - tam thức bậc hai
- Đặt t = x2, (t ≥ 0) Phương trình: at2 + bt + c = 0 (2).
- Để (1) có đúng 1 nghiệm thì (2) có nghiệm t1, t2 thỏa mãn:
- Để (1) có đúng 2 nghiệm thì (2) có nghiệm t1, t2 thỏa mãn:
- Để (1) có đúng 3 nghiệm thì (2) có nghiệm t1, t2 thỏa mãn: 0 = t1 < t2.
- Để (1) có đúng 4 nghiệm thì (2) có nghiệm t1, t2 thỏa mãn: 0 < t1 < t2.
c) Bài toán: Tìm m để (C): y = ax4 + bx2 + c (1) cắt Ox tại 4 điểm có hoành độ lập thành cấp số cộng.
- Đặt t = x2, (t ≥ 0). Phương trình: at2 + bt + c = 0 (2).
- Để (1) cắt Ox tại 4 điểm phân biệt thì (2) phải có 2 nghiệm dương t1, t2 (t1 < t2) thỏa mãn t2 = 9t1.
- Kết hợp t2 = 9t1 với Định lí Vi-et tìm được m.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Xét tương giao dựa vào xét nghiệm phương trình hoành độ giao điểm
1.1. Phương pháp giải
Cho hàm số y = f(x) có đồ thị (C1) và y = g(x) có đồ thị (C2).
Phương trình f(x) = g(x) (*) được gọi là phương trình hoành độ giao điểm.
- Số giao điểm của đồ thị (C1) và (C2) là số nghiệm của phương trình hoành độ giao điểm.
- Và khi đó, các nghiệm của phương trình (*) là các hoành độ giao điểm.
* Lưu ý:
- Trục hoành có phương trình là y = 0.
- Các đường thẳng y = m (với m là tham số thực) có đồ thị là đường thẳng song song hoặc trùng với trục Ox.
- Định lí Vi-et cho phương trình bậc hai, bậc ba.
Phương trình bậc hai: ax2 + bx + c = 0 (a ≠ 0), giả sử phương trình có 2 nghiệm x1, x2.
Phương trình bậc ba: ax3 + bx2 + cx + d = 0 (a ≠ 0), giả sử phương trình có 3 nghiệm x1; x2; x3.
⇒ Theo Định lí Vi-et ta có:
1.2. Ví dụ
Ví dụ 1. Đồ thị hàm số cắt trục hoành tại mấy điểm?
A. 4.
B. 3.
C. 2.
D. 0.
Hướng dẫn giải
Phương trình hoành độ giao điểm:
Đặt x2 = t (t ≥ 0), phương trình trở thành:
Vậy đồ thị hàm số cắt trục hoành tại 2 điểm. Chọn C.
Ví dụ 2. Gọi A, B là giao điểm của đồ thị hàm số với đường thẳng y = x - 2. Độ dài AB bằng?
A.
B. 1.
C.
D.
Hướng dẫn giải
* Xét phương trình hoành độ giao điểm:
= x - 2 2x - 1 = (x + 2)(x - 2) 2x - 1 = x2 - 4 x2 - 2x - 3 = 0 (*).
Cách 1: Không tìm tọa độ A, B
Gọi A (x1; x1 - 2); B (x2; x2 - 2) (với x1; x2 là hai nghiệm của phương trình (*))
Mà x1; x2 là nghiệm của (*), theo Vi-et ta có:
Cách 2: Tìm tọa độ A, B
. Chọn C.
Ví dụ 3. Tìm giá trị thực của tham số m để đồ thị hàm số y = x3 - 3x2 + 2 (C) cắt đường thẳng d: y = m (x - 1) tại ba điểm phân biệt có hoành độ x1; x2; x3 thỏa mãn: ?
A.
B.
C. m > -3.
D. m > -2.
Hướng dẫn giải
* Tìm điều kiện để (C) cắt d tại 3 điểm phân biệt:
Xét phương trình hoành độ giao điểm: x3 - 3x2 + 2 = m (x - 1) (*).
* Lưu ý: Casio: Tìm 1 nghiệm của phương trình bậc ba chứa m.
Gán m = 100 bấm máy giải phương trình. Nếu:
+ Có nghiệm đẹp, nhỏ:
+ Có nghiệm m = 100 phương trình có nghiệm x = m
x = 99 phương trình có nghiệm x = m - 1
x = -98 phương trình có nghiệm x = -(m - 2)
Nhận thấy phương trình (*) luôn có 1 nghiệm x = 1
⇒ (*) (x - 1) (x2 - 2x - 2) = m (x - 1)
(x - 1) (x2 - 2x - 2 - m) = 0
Để đồ thị (C) cắt d tại 3 giao điểm Phương trình (**) có 2 nghiệm phân biệt ≠ 1
* Tìm điều kiện để
Cho x3 = 1; x1, x2 là nghiệm của phương trình (**)
Theo Vi-et của phương trình (**) ta có: 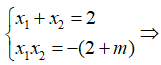
Từ (1), (2) ⇒ m > -2. Chọn D.
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Đồ thị hàm số y = -x3 + 2x2 - 1 cắt trục tung tại điểm có tung độ bằng
A. 3.
B. 1.
C. −1.
D. 0.
Câu 2. Số giao điểm của đồ thị hàm số y = -x3 + 7x với trục hoành là
A. 0.
B. 3.
C. 2.
D. 1.
Câu 3. Đồ thị hàm số y = x4 - 3x2 + 1 và đồ thị hàm số y = -2x2 + 7 có bao nhiêu điểm chung?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 4. Cho hàm số f(x) có bảng biến thiên như sau:
Số nghiệm của phương trình 3 f(x) - 2 = 0 là
A. 2.
B. 0.
C. 3.
D. 1.
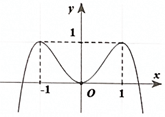
Câu 5. Cho hàm số f(x) = ax4 + bx2 + c (a, b, c ). Đồ thị của hàm số y = f(x) như hình vẽ bên.Số nghiệm của phương trình 4 f(x) - 3 = 0 là
A. 2.
B. 0.
C. 4.
D. 3.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f [f(x)] = 1 là:
Điền đáp án |
Câu 17. Cho hàm số y = f(x) có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới.
Đặt g(x) = f [f(x)]. Tìm số nghiệm của phương trình g'(x) = 0.
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Cho đồ thị hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0) như sau:
a) Khi thì phương trình f(x) = m có 1 nghiệm.
b) Khi thì phương trình f(x) = m có 3 nghiệm.
c) Hàm số có 3 điểm cực trị.
d) Hàm số cắt trục tung tại điểm có tung độ bằng 0.
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
I. LÝ THUYẾT CẦN NHỚ
1. Ứng dụng đạo hàm trong tốc độ thay đổi của một đại lượng
• Nếu s = s (t) là hàm vị trí của một vật chuyển động trên một đường thẳng thì v (t) = s' (t) biểu thị vận tốc tức thời của vật (tốc độ thay đổi của độ dịch chuyển theo thời gian). Tốc độ thay đổi tức thời của vận tốc theo thời gian là gia tốc tức thời của vật. Vậy a (t) = v' (t) = s'' (t).
• Nếu C = C (t) là nồng độ của một chất tham gia phản ứng hóa học tại thời điểm t thì C' (t) biểu thị tốc độ phản ứng tức thời (tốc độ thay đổi nồng độ) của chất đó tại thời điểm t.
• Nếu P = P (t) là số lượng cá thể trong một quần thể động vật hoặc thực vật tại thời điểm t thì P' (t) biểu thị tốc độ tăng trưởng tức thời của quần thể tại thời điểm t.
2. Ứng dụng đạo hàm trong bài toán tối ưu kinh tế, xã hội
• Nếu C = C (x) là hàm chi phí, tức là tổng chi phí khi sản xuất x đơn vị hàng hoá thì C' (x) (gọi là chi phí biên) biểu thị tốc độ thay đổi tức thời của chi phí đối với số lượng đơn vị hàng hoá được sản xuất.
• Gọi p (x) là giá bán mỗi đơn vị mà công ty có thể tính nếu bán x đơn vị. Khi đó, p được gọi là hàm cầu (hay hàm giá) và chúng ta mong đợi đó là một hàm giảm của x.
• Nếu x đơn vị được bán và giá mỗi đơn vị là p (x) thì tổng doanh thu là R (x) = x.p (x) và R (x) được gọi là hàm doanh thu.
• Đạo hàm R' (x) của hàm doanh thu được gọi là hàm doanh thu biên và là tốc độ thay đổi của doanh thu đối với số lượng đơn vị sản phẩm bán ra.
• Nếu x đơn vị được bán, thì tổng lợi nhuận là P (x) = R (x) - C (x) và P (x) được gọi là hàm lợi nhuận.
Hàm lợi nhuận biên là đạo hàm P' (x) của hàm lợi nhuận.
3. Ứng dụng đạo hàm cho các bài toán tối ưu trong các mô hình toán học
Chọn ẩn x phù hợp từ mô hình hình học, biểu diễn các yếu tố liên quan đến diện tích, thể tích được hàm số theo yêu cầu bài toán. Tìm điều kiện cho x, khảo sát hàm số và trả lời yêu cầu của bài toán.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Phương pháp giải
• Phương pháp chung:
Bước 1: Chọn ẩn phù hợp
+ Đặt cái gì là ẩn? → Cần đặt làm sao để thiết lập được đại lượng cần tìm giá trị Min, Max là dễ dàng, thuận lợi.
+ Đặt bao nhiêu ẩn?
Bước 2: Thiết lập đại lượng cần tìm Min, Max theo các ẩn đã chọn, từ giả thiết rút thế về hàm 1 ẩn.
Bước 3: Tìm Min, Max hàm số bằng phương pháp khảo sát hàm số, hoặc dùng bất đẳng thức, Casio.
• Một số bất đẳng thức cơ bản:
+ Bất đẳng thức AM – GM cho hai số thực không âm
+ Bất đẳng thức Bunhiacopxki cho các số thực a, b, c, d
Dấu “=” xảy ra khi
• Một số bổ đề cơ bản dùng trong các bài toán hai biến
và
Bất đẳng thức Cauchy - Schwarz dạng phân số
2. Ví dụ
Ví dụ 1. Người ta tiêm một loại thuốc vào mạch máu ở cánh tay phải của một bệnh nhân. Sau thời gian là t giờ, nồng độ thuốc hấp thu trong máu của bệnh nhân đó được xác định theo công thức (0 < t < 24). Hỏi sau bao nhiêu giờ thì nồng độ thuốc hấp thu trong máu của bệnh nhân đó là cao nhất?
A. 24 giờ.
B. 4 giờ.
C. 2 giờ.
D. 1 giờ.
Hướng dẫn giải
Yêu cầu bài toán: Tìm giá trị của t (0; 24) để đạt giá trị lớn nhất.
Xét hàm số trên (0; 24), có
Phương trình C' (t) = 0
Tính C (2) = 0,07.
Suy ra = C (2) = 0,07.
Vậy sau 2 giờ thì nồng độ hấp thu là cao nhất. Chọn C.
Ví dụ 2. Người ta giới thiệu một loại thuốc kích thích sự sinh sản của một loại vi khuẩn. Sau ít phút, số vi khuẩn được xác định theo công thức N (t) = 1000 + 30t2 - t3 (0 ≤ t ≤ 30). Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
A. 10 phút.
B. 20 phút.
C. 30 phút.
D. 15 phút.
Hướng dẫn giải
Yêu cầu bài toán: Tìm giá trị của t ∈ [0; 30] để N (t) = 1000 + 30t2 - t3 đạt giá trị lớn nhất.
Xét hàm số N (t) = 1000 + 30t2 - t3 trên [0; 30], có N' (t) = 60t - 3t2.
Phương trình 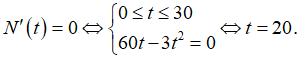
Suy ra = N (20) = 5000.
Vậy sau 20 phút thì số vi khuẩn là lớn nhất. Chọn B.
Ví dụ 3. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500 000 đồng / m2. Hãy xác định kích thước của hồ nước để chi phí thuê nhân công thấp nhất, khi đó chi phí đó là:
A. 74 triệu đồng.
B. 75 triệu đồng.
C. 76 triệu đồng.
D. 77 triệu đồng.
Hướng dẫn giải
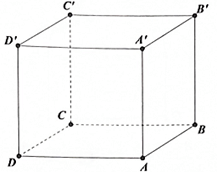
Giả sử khối hộp chữ nhật là ABCD.A'B'C'D' và AB = x, AD = 2x và AA' = h (x, h > 0).
Ta có V = x.2x.h
Diện tích cần xây là S = 2x2 + 2 (xh + 2xh) = 2x2 + 6xh.
Ta cần tìm giá trị nhỏ nhất của với x > 0.
Ta có
Dấu đẳng thức xảy ra khi
S nhỏ nhất là 150 khi x = 5.
Số tiền chi phí là: 150.500 000 = 75 000 000 đồng hay 75 triệu đồng. Chọn B.
Ví dụ 4. Một ông nông dân có 2 400 m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu?
A. 360 000 m2.
B. 702 000 m2.
C. 630 000 m2.
D. 720 000 m2.
Hướng dẫn giải
Gọi hai kích thước của hình chữ nhật là x và y, với 2x + y = 2400 (0 < x, y < 2400).
Diện tích của mảnh vườn hình chữ nhật là:
Vậy ông nông dân có thể rào được cánh đồng với diện tích lớn nhất là 720 000 m2. Chọn D.
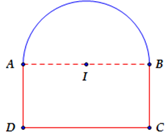
Ví dụ 5. Một cửa sổ có hình dạng như hình bên, bao gồm: một hình chữ nhật ghép với nửa hình tròn có tâm nằm trên cạnh của hình chữ nhật. Biết rằng tổng độ dài đường viền cho phép của cửa sổ là 4 m. Hỏi diện tích lớn nhất của cửa sổ là bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
Gọi
Suy ra và
Tổng diện tích của cửa sổ là
Do đó diện tích lớn nhất của cửa sổ là Chọn B.
................................
................................
................................
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Một vật chuyển động theo quy luật với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 24 (m/s).
B. 27 (m/s).
C. 144 (m/s).
D. 36 (m/s).
Câu 2. Cho số a > 0. Trong số các tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng a, tam giác có diện tích lớn nhất bằng
A.
B.
C.
D.
Câu 3. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức (mg/ L). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ.
B. 1 giờ.
C. 3 giờ.
D. 2 giờ.
Câu 4. Ông A muốn mua một mảnh đất hình chữ nhật có diện tích bằng 100 m2 để làm khu vườn. Hỏi người đó phải mua mảnh đất có kích thước như thế nào để chi phí xây dựng bờ rào là ít tốn kém nhất?
A. 10 m × 10 m.
B. 4 m × 25 m.
C. 5 m × 20 m.
D. 25 m × 8 m.
Câu 5. Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao cho thể tích khối hộp được tạo thành là 8 dm3 và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là
A. dm.
B. 2 dm.
C. 4 dm.
D. dm.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Một công ty chuyên sản xuất dụng cụ thể thao nhận được đơn đặt hàng sản xuất 8000 quả bóng rổ. Công ty có một số máy móc, mỗi máy có khả năng sản xuất 30 bóng rổ trong một giờ. Chi phí thiết lập mỗi máy là 200 nghìn đồng. Sau khi thiết lập, quá trình sản xuất sẽ diễn ra hoàn toàn tự động và chỉ cần có người giám sát. Chi phí trả cho người giám sát là 192 nghìn đồng mỗi giờ. Công ty cần sử dụng bao nhiêu máy móc để chi phí hoạt động đạt mức thấp nhất?
Điền đáp án |
Câu 17. Một bài báo trong tạp chí xã hội học phát biểu rằng nếu một chương trình chăm sóc sức khỏe đặc biệt cho người già được khởi xướng, thì t năm sau khi nó được khởi động, n ngàn người già có thể trực tiếp nhận được các phúc lợi, trong đó . Với giá trị nào của t thì số người nhận phúc lợi tối đa là bao nhiêu?
Điền đáp án |
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Từ một tấm bìa hình vuông ABCD có cạnh bằng MA2 = MB2 + MC2 người ta cắt bỏ bốn tam giác cân bằng nhau là AMB, BNC, CPD và DQA. Với phần còn lại người ta gấp lên và ghép lại để thành hình chóp tứ giác đều.
Gọi cạnh đáy của mô hình là x (cm) với x > 0.
a) Chiều cao của hình chóp là
b) Điều kiện của x là: 0 < x <
c) Thể tích của khối chóp bằng
d) Khi cạnh đáy của khối chóp bằng dm thì thể tích của khối chóp là lớn nhất.
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGNL HSA) Chuyên đề: Góc, khoảng cách trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Thể tích của một số hình khối
- (Ôn thi ĐGNL HSA) Chuyên đề: Nguyên hàm - Tích phân
- (Ôn thi ĐGNL HSA) Chuyên đề: Vectơ và phương pháp tọa độ trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Thống kê và xác suất
- (Ôn thi ĐGNL HSA) Chuyên đề: Một số câu hỏi trích trong các đề thi tham khảo
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

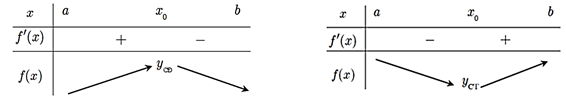
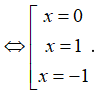
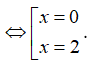
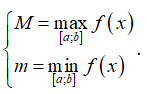
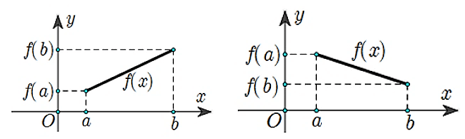
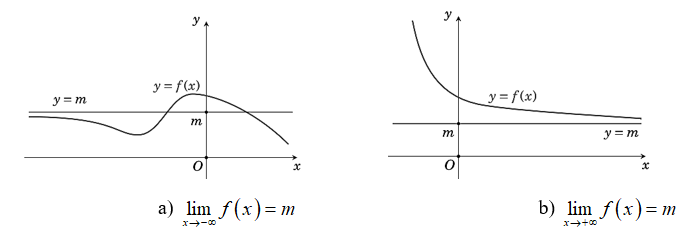
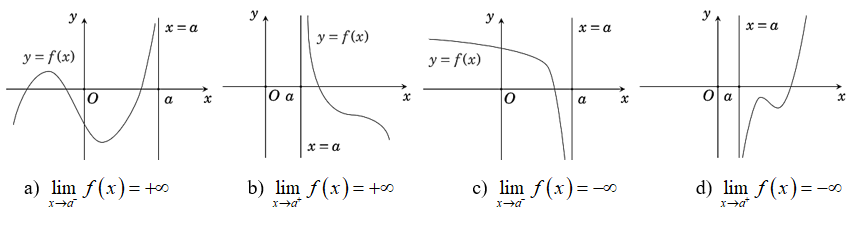
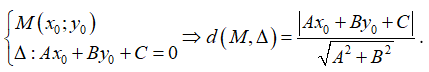
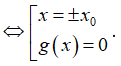
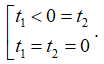
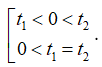
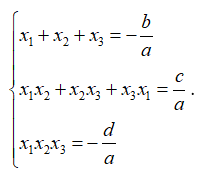
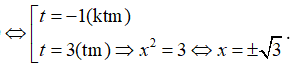
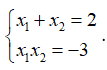
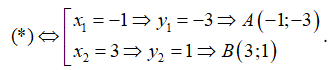
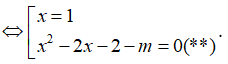
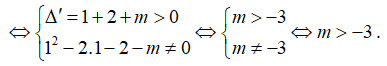
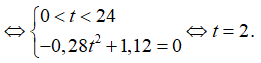
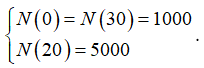
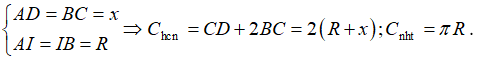



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

