(Ôn thi ĐGNL, ĐGTD) Tích phân hàm ẩn
Chủ đề Tích phân hàm ẩn trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Tích phân hàm ẩn
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
I. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Sử dụng phương pháp nguyên hàm, tích phân từng phần
1.1. Phương pháp giải
• Để đưa từ Nguyên hàm - Tích phân chứa f(x) về Nguyên hàm - Tích phân chứa f'(x) ta làm như sau: Đặt u = f(x), dv là phần còn lại.
• Để đưa từ Nguyên hàm - Tích phân chứa f'(x) về Nguyên hàm - Tích phân chứa f(x) ta làm như sau: Đặt dv = f'(x) dx, u là phần còn lại.
* Lưu ý: Kỹ năng chọn hằng số C trong việc tìm v trong một số tình huống bài toán.
1.2. Ví dụ
Ví dụ 1. Cho hàm số f(x) liên tục trên . Biết cos 2x là một nguyên hàm của hàm số f(x) ex, họ tất cả các nguyên hàm của hàm số f'(x) ex là
A. -sin 2x + cos 2x + C.
B. -2sin 2x + cos 2x + C.
C. -2sin 2x - cos 2x + C.
D. 2sin 2x - cos 2x + C.
Hướng dẫn giải
Đi tìm I = f'(x) .ex dx → Dùng nguyên hàm từng phần để đưa về nguyên hàm chứa f(x).
Đặt
I = ex.f(x) - f(x)ex dx = ex.f(x) - cos 2x + C.
Mà (cos 2x)' = f(x).ex -2sin 2x = f(x).ex
I = -2sin 2x - cos 2x + C. Chọn C.
Ví dụ 2. Cho hàm số f(x) có f(3) = 3 và Tính
Hướng dẫn giải
Cách 1: Tích phân cần tìm chứa f(x):
Đặt
Chọn C sao cho 8 + C = 0 C = -8.
Cách 2: Tìm f(x):
Ví dụ 3. Cho hàm số f(x) có f(0) = 0 và f'(x) = sin4 x, . Tích phân bằng:
A.
B.
C.
D.
Hướng dẫn giải
Đặt
. Chọn C.
................................
................................
................................
II. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Cho hàm số f(x) liên tục trên . Biết cos2 x là một nguyên hàm của hàm số f(x) e2x, họ tất cả các nguyên hàm của hàm số f'(x) e2x là:
A. sin 2x - 2cos2 x + C.
B. sin 2x + 2cos2 x + C.
C. -sin 2x + 2cos2 x + C.
D. -sin 2x - 2cos2 x + C.
Câu 2. Cho là một nguyên hàm của hàm số Tìm họ nguyên hàm của hàm số f'(x).ln x.
A.
B.
C.
D.
Câu 3. Cho hàm số f(x). Biết f(0) = 4 và f'(x) = 2sin2 x + 3, . Khi đó bằng:
A.
B.
C.
D.
Câu 4. Cho hàm số f(x) liên tục trên (0; +∞) thỏa mãn f(1) = e và x3 f'(x) = ex (x - 2), Tính
A. 3 - e.
B. 2 - e.
C. 3 + e.
D. 2 + e.
Câu 5. Cho hàm số f(x) > 0 với , f(0) = 1 và f(x) = .f'(x) với Hỏi mệnh đề nào đúng?
A. 4 < f(3) < 6.
B. f(3) < 2.
C. 2 < f(3) < 4.
D. f(3) > 6.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 11. Cho hàm số f(x) có f(16) = 8 và Khi đó bằng:
Câu 12. Cho hàm số f(x) liên tục trên (0; +∞), thỏa mãn 2x. f'(x) + f(x) = 3x2. Biết f(1) = . Tính f(4).
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGNL HSA) Chuyên đề: Góc, khoảng cách trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Thể tích của một số hình khối
- (Ôn thi ĐGNL HSA) Chuyên đề: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
- (Ôn thi ĐGNL HSA) Chuyên đề: Vectơ và phương pháp tọa độ trong không gian
- (Ôn thi ĐGNL HSA) Chuyên đề: Thống kê và xác suất
- (Ôn thi ĐGNL HSA) Chuyên đề: Một số câu hỏi trích trong các đề thi tham khảo
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

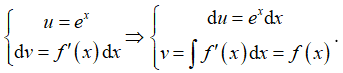
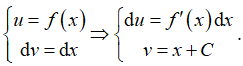
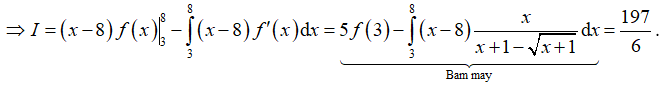
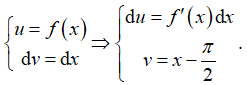



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

