Giáo án Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn (mới, chuẩn nhất)
Giáo án Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Chỉ từ 300k mua trọn bộ Kế hoạch bài dạy (KHBD) hay Giáo án Toán 10 cả năm (mỗi bộ sách) bản word chuẩn kiến thức, trình bày đẹp mắt:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
A. KẾ HOẠCH CHUNG
Tiết 1 |
HOẠT ĐỘNG KHỞI ĐỘNG |
|
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC |
Bất phương trình bậc nhất hai ẩn |
|
Biểu diễn nghiệm của bất phương trình bậc nhất hai ẩn |
||
Hệ bật phương trình bậc nhất hai ẩn |
||
Tiết 2 |
HOẠT ĐỘNG LUYỆN TẬP, VẬN DỤNG |
|
HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG |
||
B. KẾ HOẠCH DẠY HỌC
I. Mục tiêu
Qua bài học HS cần:
1. Kiến thức:
- Hiểu khái niệm bất phương trình và hệ bất phương trình bậc nhất hai ẩn, nghiệm và miền nghiệm của chúng.
2. Kỹ năng:
- Biểu diễn được tập nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ, gáp dụng giải được bài toán thức tế.
3. Về tư duy và thái độ:
-Tích cực hoạt động, trả lời các câu hỏi. Biết quan sát phán đoán chính xác, biết quy lạ về quen.
4. Các năng lực chính hướng tới sự hình thành và phát triển ở học sinh:
- Năng lực hợp tác; Năng lực tự học, tự nghiên cứu; Năng lực giải quyết vấn đề; Năng lực sử dụng công nghệ thông tin; Năng lực thuyết trình, báo cáo; Năng lực tính toán.
II. Chuẩn bị:
HS: Nghiên cứu và sọan bài trước khi đến lớp.
GV: Giáo án, các dụng cụ học tập, phiếu học tập,…
III.Phương pháp:
Về cơ bản gợi mở, phát vấn, giải quyết vấn đề và đan xen hoạt động nhóm.
IV. Tiến trình dạy học:
1. Giới thiệu (Hoạt động khởi động):
Trong sản suất, kinh doanh cũng như trong các hoạt động cuộc sống thì vấn đề hiệu quả, tối ưu luôn được đặt ra đầu tiên, làm thế nào để đạt hiệu quả cao nhất trong một công việc nào đó.
Ngoài việc cải tiến công nghệ, thì cải tiến phương pháp, bố trí lao động chính là một giải pháp quan trọng để nâng cao hiệu quả công việc.
Sau đây là một ví dụ:
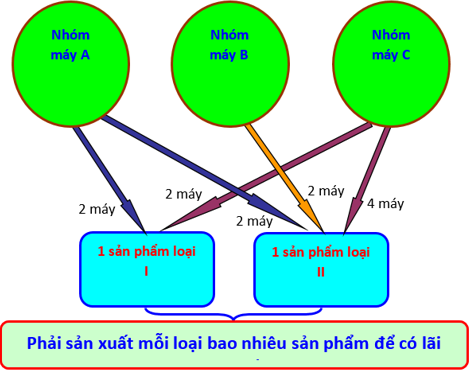
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II.
Để sản xuất một đơn vị sản phẩm mỗi loại I cần 2 máy thuộc nhóm A, 2 máy thuộc nhóm C;
để sản xuất một đơn vị sản phẩm mỗi loại II cần 2 máy thuộc nhóm A, 2 máy thuộc nhóm B, 4 máy thuộc nhóm C.
Một đơn vị sản phẩm I lãi 3 nghìn đồng, một đơn vị sản phẩm II lãi 5 nghìn đồng.
Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất biết rằng số máy trong mỗi nhóm A, B, C lần lượt là 10, 4 và 12 máy.
2. Nội dung chính (Hoạt động hình thành kiến thức).
2.1. Bất phương trình bậc nhất hai ẩn.
a) Tiếp cận:
- Vẽ đường thẳng d:x+y=2 .
- Chọn một số điểm không nằm trên đường thẳng.
- Thay tọa độ các điểm trên vào biểu thức x+y và so sánh các giá trị tìm được với 2.
b) Khái niệm:
Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là ax+by≤c (1)
(ax+y<c;ax+y>c;ax+y≥c) trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Ví dụ: x+3y ≤ 2, y≤2, x-3y≤8 .
c) Củng cố:
Ví dụ 1: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn.
(I)y>-2, (II)x-3y3≥6, (III)x+y≤2
Ví dụ 2: Hãy lấy một ví dụ khác về bất phương trình bậc nhất hai ẩn và một ví dụ về bất phương trình nhưng không phải là bất phương trình bậc nhất hai ẩn.
2.2 Biểu diễn nghiệm của bất phương trình bậc nhất hai ẩn.
a) Tiếp cận:
- Hãy tìm một số nghiệm của bất phương trình x+y≤2 .
- Có thể liệt kê hết tất cả các nghiệm của bất phương trình trên không?
b) Khái niệm:
* Miền nghiệm:
Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm bất phương trình (1) được gọi là miền nghiệm của nó.
*Quy tắc tìm miền nghiệm:
Bước 1: Trên mặt phẳng tọa độ Oxy , vẽ đường thẳng d:ax+by=c .
Bước 2: Lấy một điểm M(x0,y0) không phụ thuộc d (ta thường lấy gốc tọa độ O ).
Bước 3: Tính ax0+by0 và so sánh ax0+by0 với c.
Bước 4: Kết luận
Nếu ax+by<c thì nửa mặt phẳng bờ d chứa M0 là miền nghiệm của ax+by≤c.
Nếu Nếu ax+by>c thì nửa mặt phẳng bờ d không chứa M0 là miền nghiệm của ax+by≤c .
CHÚ Ý: Miền nghiệm của bất phương trình ax+by≤c bỏ đi đường thẳng ax+by=c là miền nghiệm của bất phương trình ax+by<c .
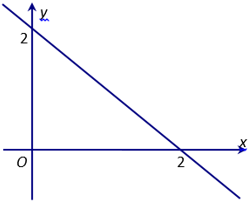
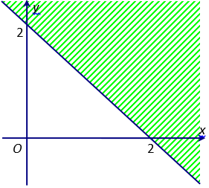
Ví dụ 1: Biểu diễn miền nghiệm của bất phương trình x+y≤2 .
- Vẽ đường thẳng d:x+y=2
- Nhận thấy (0,0) là nghiệm của bất phương trình, nên miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là d (kể cả bờ) và chứa gốc tọa độ O
c) Củng cố
Ví dụ 2: Biểu diễn miền nghiệm của bất phương trình 4x-3y≤6 .
2.3. Hệ bất phương trình bậc nhất hai ẩn.
a) Tiếp cận: Trong bài toán trên, gọi x,y là số sản phẩm loại I và II được sản suất. Viết tất cả các điều kiện của x,y .
b) Khái niệm:
Tương tự hệ bất phương trình một ẩn
Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất nhất hai ẩn x,y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho
Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.
Quy tắc tìm miền nghiệm của hệ bất phương trình:
- Biểu diễn miền nghiệm của từng bất phương trình trên cùng một hệ trục tọa độ.
- Miền nghiệm của hệ là giao của tất cả các miền nghiệm của các bất phương trình của hệ.
c) Củng cố:
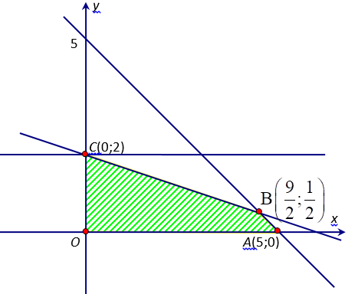
Ví dụ: Biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC
d) Vận dụng:
Phải sản xuất mỗi loại bao nhiêu sản phẩm để có lãi cao nhất?
Số tiền lãi thu được là L=3x+5y (nghìn đồng).
L đạt giá trị lớn nhất khi tại một trong các đỉnh của tứ giác OABC .
Tính giá trị của biểu thức L tại các đỉnh O,A,B,C ta thấy L lớn nhất bằng 16 khi
.....................................................................................................
.....................................................................................................
.....................................................................................................
.....................................................................................................
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Xem thêm các bài soạn Giáo án Toán lớp 10 theo hướng phát triển năng lực mới nhất, hay khác:
- Giáo án Toán 10 Bài 1: Bất đẳng thức
- Giáo án Toán 10 Bài 2: Bất phương trình và hệ bất phương trình một ẩn
- Giáo án Toán 10 Bài 3: Dấu của nhị thức bậc nhất
- Giáo án Toán 10 Bài 5: Dấu của tam thức bậc hai
- Giáo án Toán 10 Ôn tập chương 4 Đại số
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giáo án Toán 10 cả ba sách mới của chúng tôi được biên soạn bám sát chuẩn Giáo án môn Toán 10 của Bộ GD & ĐT.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 10 (các môn học)
- Giáo án điện tử lớp 10 (các môn học)
- Giáo án Ngữ văn 10
- Giáo án Toán 10
- Giáo án Tiếng Anh 10
- Giáo án Vật Lí 10
- Giáo án Hóa học 10
- Giáo án Sinh học 10
- Giáo án Lịch Sử 10
- Giáo án Địa Lí 10
- Giáo án Kinh tế Pháp luật 10
- Giáo án Tin học 10
- Giáo án Công nghệ 10
- Giáo án Giáo dục quốc phòng 10
- Giáo án Hoạt động trải nghiệm 10
- Đề thi lớp 10 (các môn học)
- Đề thi Ngữ Văn 10 (có đáp án)
- Chuyên đề Tiếng Việt lớp 10
- Đề cương ôn tập Văn 10
- Đề thi Toán 10 (có đáp án)
- Đề thi cương ôn tập Toán 10
- Đề thi Toán 10 cấu trúc mới (có đáp án)
- Đề thi Tiếng Anh 10 (có đáp án)
- Đề thi Vật Lí 10 (có đáp án)
- Đề thi Hóa học 10 (có đáp án)
- Đề thi Sinh học 10 (có đáp án)
- Đề thi Lịch Sử 10 (có đáp án)
- Đề thi Địa Lí 10 (có đáp án)
- Đề thi Kinh tế & Pháp luật 10 (có đáp án)
- Đề thi Tin học 10 (có đáp án)
- Đề thi Công nghệ 10 (có đáp án)
- Đề thi Giáo dục quốc phòng 10 (có đáp án)


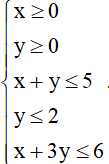
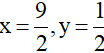



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

