Tổng hợp lý thuyết Toán lớp 5 Chương 3 Hình học hay, chi tiết

Tổng hợp lý thuyết Toán lớp 5 Chương 3 Hình học hay, chi tiết

Tổng hợp, tóm tắt kiến thức trọng tâm Toán lớp 5 Chương 3: Hình học với lý thuyết đầy đủ, chi tiết và cách giải các dạng bài tập giúp học sinh học tốt môn Toán lớp 5.

• Toán lớp 5 Hình tam giác - Diện tích hình tam giác

• Toán lớp 5 Hình thang - Diện tích hình thang

• Toán lớp 5 Hình tròn - Đường tròn - Chu vi hình tròn

• Toán lớp 5 Diện tích hình tròn

• Toán lớp 5 Hình hộp chữ nhật - Hình lập phương

• Toán lớp 5 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

• Toán lớp 5 Diện tích xung quanh và diện tích toàn phần của hình lập phương

• Toán lớp 5 Thể tích của một hình - Xăng - ti - mét khối. Đề - xi - mét khối

• Toán lớp 5 Thể tích hình hộp chữ nhật

• Toán lớp 5 Thể tích hình lập phương

---

---

---

Toán lớp 5 Hình tam giác - Diện tích hình tam giác

1. Hình tam giác

a) Cấu trúc

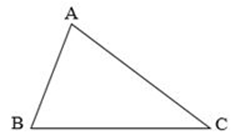
Hình tam giác ABC có: 

- Ba cạnh là : cạnh AB, cạnh AC, cạnh BC.

- Ba đỉnh là : đỉnh A, đỉnh B, đỉnh C.

- Ba góc là:

Góc đỉnh A, cạnh AB và AC ( gọi tắt là góc A) 

Góc đỉnh B, cạnh BA và BC ( gọi tắt là góc B) 

Góc đỉnh C, cạnh CA và CB ( gọi tắt là góc C) 

b) Các loại hình tam giác

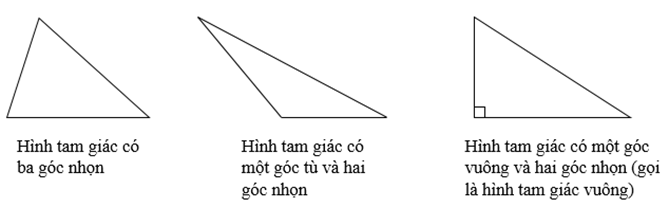
c) Cách xác định đáy và đường cao của hình tam giác

                                               

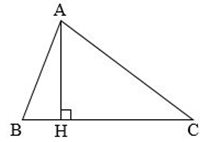
        BC là đáy, AH là đường cao tương ứng với đáy BC. Độ dài AH là chiều cao.

                                                          

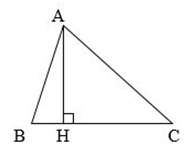
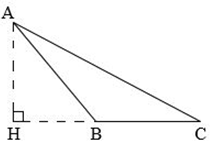
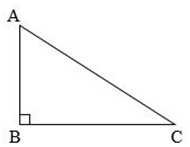
AH là đường cao ứng với đáy BC        AH là đường cao ứng với BC              AB là đường cao ứng với đáy BC

Chú ý: Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác

2. Diện tích hình tam giác

Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2

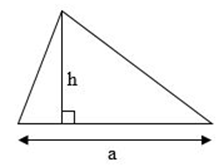
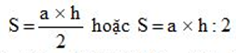
( S là diện tích, a là độ dài đáy, h là chiêu cao)

Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.

Phương pháp giải: Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2.

Cách giải:

Diện tích hình tam giác đó là:

            13 x 8 : 2 = 52 (cm²)                       

Đáp số: 52cm²

Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm.

Phương pháp giải: Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, 2m = 20dm, sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2

Bài giải

Đổi: 2m = 20dm

Diện tích hình tam giác đó là:

20 x 15 : 2 = 150 dm²

Đáp số: 150 dm²

3) Một số dạng bài tập

Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao

Phương pháp: Áp dụng công thức S= 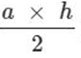 hoặc S= a x h : 2

(S là diện tích, a là độ dài đáy, h là chiều cao)

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao

Phương pháp: Từ công thức tính diện tích S= 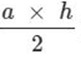   hoặc S= a x h : 2, ta có công thức tính độ dài đáy như sau:

a= 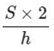   hoặc a= S x2 : h

Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy

Phương pháp: Từ công thức tính diện tích S= 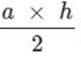   hoặc S= a x h: 2, ta có công thức tính chiều cao như sau

h= 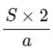   hoặc h= S x 2 : a.

Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

Toán lớp 5 Hình thang - Diện tích hình thang

1. Hình thang

a) Định nghĩa

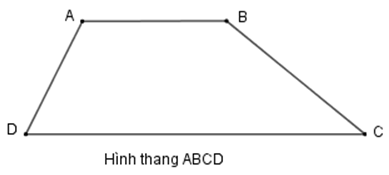
Hình thang ABCD có:

- Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.

- Hai cạnh đáy là hai cạnh đối diện song song.

Hình thang có một cặp cạnh đối diện song song.

Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.

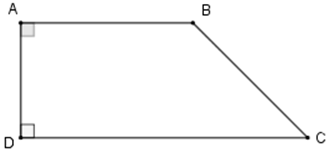
b) Đường cao của hình thang

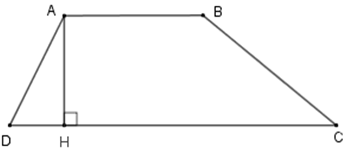
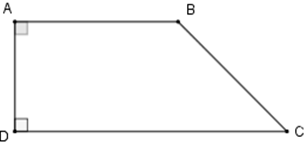
AH là đường cao. Độ dài AH là chiều cao               AD là đường cao. Độ dài AD là chiều cao

2. Diện tích hình thang

Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho2.

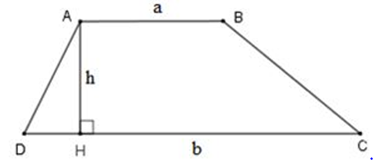
( S là diện tích; a, b là độ dài các cạnh đáy ; h là chiều cao)

Ví dụ 1: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18cm và 14cm; chiều cao là 9cm.

Phương pháp giải: Độ dài hai đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Diện tích hình thang đó là:

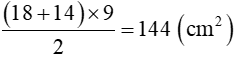
                             Đáp số: 144 (cm²)

Ví dụ 2: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 4m và 25dm; chiều cao là 32dm.

Phương pháp giải: Độ dài hai đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đó, 4m = 40dm, sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Đổi: 4m = 40dm

Diện tích hình thang đó là:

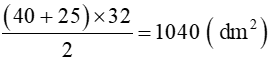
Đáp số: 1040dm²

3. Một số dạng bài tập

Dạng 1: Tính diện tích hình thang khi biết độ dài hai đáy và chiều cao

Phương pháp: 

Áp dụng công thức: 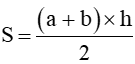 hoặc S= (a+b) x h : 2

( là diện tích, là độ dài các cạnh đáy, là chiều cao)

Dạng 2: Tính tổng độ dài hai đáy khi biết diện tích và chiều cao

Phương pháp: Từ công thức tính diện tích 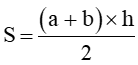hoặc S= ( a+b) x h : 2 ta có công thức tính độ dài hai đáy như sau: a+b = S x h : 2

Lưu ý: Đề bài thường cho hiệu của hai đáy hoặc tỉ số giữa hai đáy và yêu cầu tìm độ dài của mỗi đáy. Học sinh cần nhớ hai dạng toán tổng – hiệu và tổng – tỉ.

Dạng 3: Tính chiều cao khi biết diện tích và độ dài hai đáy

Phương pháp: Từ công thức tính diện tích 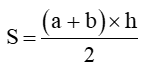 hoặc S= ( a+b) x h:2, ta có công thức tính chiều cao như sau  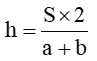hoặc h = S x2 : ( a + b).

Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

....................................

....................................

....................................

Xem thêm các bài tóm tắt lý thuyết, công thức Toán lớp 5 hay, chi tiết khác:

• Chương 1: Ôn tập và bổ sung về phân số. Giải toán liên quan đến tỉ lệ. Bảng đơn vị đo diện tích
• Chương 2: Số thập phân. Các phép toán với số thập phân
• Chương 4: Số đo thời gian. Toán chuyển động đều

---