Tập hợp. Các phép toán trên tập hợp lớp 10 (Lý thuyết Toán 10 Cánh diều)
Với tóm tắt lý thuyết Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
Tập hợp. Các phép toán trên tập hợp lớp 10 (Lý thuyết Toán 10 Cánh diều)
(199k) Xem Khóa học Toán 10 CD
Bài giảng: Bài 2: Tập hợp. Các phép toán trên tập hợp - Cô Nguyễn Hồng Thanh (Giáo viên VietJack)
Lý thuyết Tập hợp. Các phép toán trên tập hợp
1. Tập hợp
• Tập hợp (còn gọi là tập) là một khái niệm cơ bản trong toán học.
Để chỉ x là một phần tử của tập hợp A, ta viết x ∈ A (đọc là x thuộc A)
Để chỉ x không phải một phần tử của tập hợp A, ta viết x ∉ A (đọc là x không thuộc A)
• Biểu diễn tập hợp bằng một trong 2 cách:
+ Liệt kê các phần tử của tập hợp.
+ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ: Biểu diễn tập hợp B gồm các số tự nhiên có một chữ số và chia hết cho 3.
+ Liệt kê các phần tử: B = {0; 3; 6; 9}
+ Chỉ ra tính chất đặc trưng của các phần tử: B = {x ∈ ℕ | 0 ≤ x ≤ 9 và x ⋮ 3}
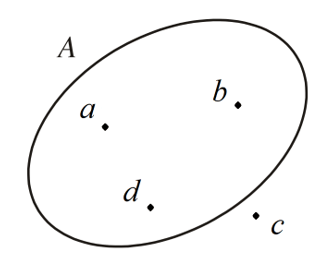
• Minh hoạ tập hợp bằng biểu đồ Ven. Mỗi phần tử thuộc tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp được biểu diễn bởi một chấm bên ngoài vòng kín.
Ở hình dưới, các phần tử thuộc tập hợp A là a, b, d; phần tử không thuộc tập hợp A là c.
• Một tập hợp có thể không có phần tử nào, có một phần tử, có nhiều phần tử, có vô số phần tử. Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng, kí hiệu là .
Chú ý: Khi C là tập hợp rỗng, ta viết C = , không được viết .
2. Tập hợp con và tập hợp bằng nhau
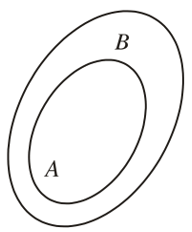
• Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của tập B, kí hiệu là A ⊂ B. Ta còn đọc là A chứa trong B.
Quy ước: Tập hợp rỗng là tập con của mọi tập hợp.
Chú ý:+ A ⊂ B ⇔ (∀x, x ∈ A ⇒ x ∈ B).
+ Khi A ⊂ B, ta cũng viết B ⊃ A, đọc là B chứa A.
+ Nếu A không phải tập con của B, ta viết A ⊄ B.
Ví dụ: Cho hai tập hợp A = {n ∈ ℕ | n⋮9} và B = {n ∈ ℕ | n⋮3}. Chứng minh A ⊂ B.
Hướng dẫn giải
Với mọi số tự nhiên n ∈ A thì n chia hết cho 9
⇒ n = 9k = 3(3k) (k ∈ ℕ)
⇒ n cũng chia hết cho 3, tức là n ∈ B.
Do đó A ⊂ B.
Tính chất:
+ A ⊂ A với mọi tập hợp A.
+ Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
• Khi A ⊂ B và B ⊂ A thì ta nói hai tập hợp A và B bằng nhau, viết là A = B.
Ví dụ: Cho tập hợp C gồm các tứ giác có 4 cạnh bằng nhau và tập hợp D gồm các hình thoi. Ta thấy:
+ Mọi tứ giác có 4 cạnh bằng nhau đều là hình thoi, tức là C ⊂ D.
+ Ngược lại, mọi hình thoi đều có 4 cạnh bằng nhau, tức là D ⊂ C.
Do đó hai tập hợp C và D bằng nhau.
3. Giao của hai tập hợp:
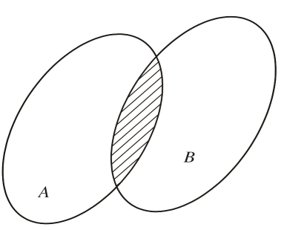
• Tập hợp gồm tất cả các phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu A ∩ B.
Vậy A ∩ B = {x | x ∈ A và x ∈ B}.
Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.
Ví dụ:
Tìm giao của tập hợp A = {x ∈ ℕ | 18 ⋮ x} và B = {x ∈ ℕ | 30 ⋮ x}
Hướng dẫn giải
Tập hợp A gồm các số tự nhiên thỏa mãn là ước của 18. Khi đó A = {1; 2; 3; 6; 9; 18}.
Tập hợp B gồm các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vậy A ∩ B = {1; 2; 3; 6}.
4. Hợp của hai tập hợp:
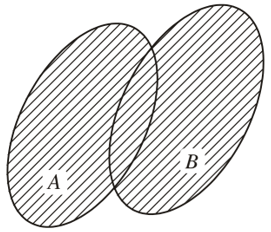
• Tập hợp gồm tất cả các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B, kí hiệu A ∪ B.
Vậy A ∪ B = {x | x ∈ A và x ∈ B}.
Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.
Ví dụ: Tìm hợp của tập hợp A = {x ∈ ℕ | 18 ⋮ x} và B = {x ∈ ℕ | 30 ⋮ x}
Hướng dẫn giải
Tập hợp A gồm các số tự nhiên thỏa mãn là ước của 18. Khi đó A = {1; 2; 3; 6; 9; 18}.
Tập hợp B gồm các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vậy A ∪ B = {1; 2; 3; 5; 6; 9; 10; 15; 18; 30}
5. Phần bù và hiệu của hai tập hợp:
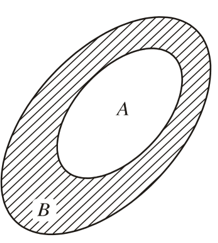
• Cho A ⊂ B. Tập hợp những phần tử của B mà không phải phần tử của A được gọi là phần bù của A trong B, kí hiệu CBA.
Vậy, khi A ⊂ B ta có CBA = {x | x ∉ A và x ∈ B}.
Tập hợp CBA được mô tả bằng phần gạch chéo trong hình dưới.
Ví dụ: Tìm phần bù của tập hợp A = {x ∈ ℕ | 10 ⋮ x} và B = {x ∈ ℕ | 30 ⋮ x}
Hướng dẫn giải
Tập hợp A là tập các số tự nhiên thỏa mãn là ước của 10. Khi đó A = {1; 2; 5; 10}.
Tập hợp B là tập các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}
Vậy CBA = {3; 6; 15; 30}.
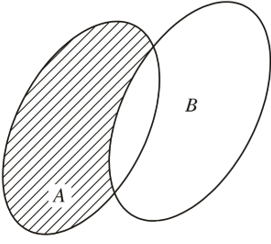
• Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B, kí hiệu A \ B.
Vậy A \ B = {x | x ∈ A và x ∉ B}.
Tập hợp A \ B được minh hoạ bởi phần gạch chéo trong hình dưới.
Ví dụ: Tìm phần bù của tập hợp A = {x ∈ ℕ | 20 ⋮ x} và B = {x ∈ ℕ | 30 ⋮ x}
Hướng dẫn giải
Tập hợp A là tập các số tự nhiên thỏa mãn là ước của 20. Khi đó A = {1; 2; 4; 5; 10; 20}.
Tập hợp B là tập các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}
Vậy A \ B = {4; 20}
6. Các tập hợp số:
• Các tập hợp ℕ, ℤ, ℚ, ℝ lần lượt là tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực.
Ta có quan hệ sau: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.
• Một số tập con thường dùng của tập số thực:
|
Tập hợp |
Tên gọi và kí hiệu |
Biểu diễn trên trục số |
|
ℝ |
Tập hợp số thực (−∞; +∞) |
|
|
{x ∈ ℝ | a ≤ x ≤ b} |
Đoạn [a; b] |
|
|
{x ∈ ℝ | a < x < b} |
Khoảng (a; b) |
|
|
{x ∈ ℝ | x > a} |
Khoảng (a; +∞) |
|
|
{x ∈ ℝ | x < b} |
Khoảng (−∞; b) |
|
|
{x ∈ ℝ | a ≤ x < b} |
Nửa khoảng [a; b) |
|
|
{x ∈ ℝ | a < x ≤ b} |
Nửa khoảng (a; b] |
|
|
{x ∈ ℝ | x ≥ a} |
Nửa khoảng [a; +∞) |
|
|
{x ∈ ℝ | x ≤ b} |
Nửa khoảng (−∞; b] |
|
Kí hiệu −∞ đọc là âm vô cực, kí hiệu +∞ đọc là dương vô cực. a và b là các đầu mút của các đoạn, khoảng, nửa khoảng.
Ví dụ: Đọc tên, kí hiệu và biểu diễn mỗi tập hợp sau trên trục số:
a) A = {x ∈ ℝ | −1 ≤ x < 2}
b) B = {x ∈ ℝ | 3x − 4 < 0}
Hướng dẫn giải
a) Tập A là nửa khoảng [−1; 2) và được biểu diễn là:
b) Tập B là khoảng và được biểu diễn là:
Bài 1. Liệt kê các phần tử của tập hợp A các số nguyên tố nhỏ hơn 7 và tập hợp B các ước số tự nhiên của 30. Xác định các tập hợp A ∩ B, A ∪ B, A \ B, CBA.
Hướng dẫn giải:
Tập hợp A là tập các số nguyên tố nhỏ hơn 7. Khi đó A = {2; 3; 5}.
Tập hợp B là tập các ước số tự nhiên của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vì tất cả các phần tử của tập hợp A đều thuộc tập hợp B nên ta có A ⊂ B.
Khi đó ta có:
A ∩ B = {2; 3; 5} = A
A ∪ B = {1; 2; 3; 5; 6; 10; 15; 30} = B
A \ B =
CBA = {1; 6; 10; 15; 30}
Bài 2. Xác định mỗi tập hợp số sau và biểu diễn nó trên trục số:
a) A = [−3; 3) ∪ (−1; 4);
b) B = (−1; 3) ∩ [0; 5]
c) C = ℝ \ (5; +∞);
d) D = (−2; 2] ∩ [1; 3)
Hướng dẫn giải
a) Ta có: [−3; 3) = {x ∈ | − 3 ≤ x < 3} và (−1; 4) = {x ∈ | − 1 < x < 4}
⇒ A = [−3; 3) ∪ (−1; 4) = {x ∈ | − 3 ≤ x < 4}
⇒ A = [−3; 4) và được biểu diễn là:
b) Ta có: (−1; 3) = {x ∈ | − 1 < x < 3} và [0; 5] = {x ∈ | − 1 ≤ x ≤ 4}
⇒ B = (−1; 3) ∩ [0; 5] = {x ∈ |− 1 < x < 3}
⇒B = [0; 3) và được biểu diễn là:
c) Tập hợp C biểu diễn những phần tử thuộc tập số thực nhưng không thuộc tập (5; +∞) nên C = (−∞; 5] và được biểu diễn là:
d) Ta có: D = (−2; 2] = {x ∈ | − 2 < x ≤ 2}và [1; 3) = {x ∈ | 1 ≤ x < 3}
⇒ D = (−2; 2] ∩ [1; 3) = {x ∈ | 1 ≤ x ≤ 2}
⇒ D = [1; 2] và được biểu diễn là:
Bài 3. Xét mối quan hệ bao hàm (tập hợp con) giữa các tập hợp sau: A là tập hợp các hình vuông, B là tập hợp các hình chữ nhật, C là tập hợp các hình thoi, D là tập hợp các bình hành.
Hướng dẫn giải
Mọi hình vuông đều có 4 góc vuông nên đều là hình chữ nhật
⇒ A ⊂ B
Mọi hình vuông đều có 4 cạnh bằng nhau nên đều là hình thoi
⇒ A ⊂ C
Mọi hình vuông đều có 2 cặp cạnh đối song song nên đều là hình bình hành
⇒ A ⊂ D
Mọi hình chữ nhật đều có 2 cặp cạnh đối song song nên đều là hình bình hành
⇒ B ⊂ D
Mọi hình thoi đều có 2 cặp cạnh đối song song nên đều là hình bình hành
⇒ C ⊂ D
Bài 4. Trong số 45 học sinh của lớp 10A có 15 học sinh giỏi, 20 học sinh được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi vừa có hạnh kiểm tốt. Hỏi lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải đạt học lực giỏi hoặc có hạnh kiểm tốt?
Hướng dẫn giải
Gọi G là tập hợp các bạn đạt học lực giỏi, T là tập hợp các bạn đạt hạnh kiểm tốt. Số học sinh được khen thưởng là số phần tử của tập hợp G ∪ T.
Ta đếm số phần tử của G (15 bạn), sau đó đếm số phần tử của T (20 bạn). Nhưng khi đó số phần tử của G ∩ T (10 bạn) lại được đếm 2 lần.
Vậy số phần tử của G ∪ T là 15 + 20 – 10 = 25.
Có 25 bạn được khen thưởng.
Học tốt Tập hợp. Các phép toán trên tập hợp
Các bài học để học tốt Tập hợp. Các phép toán trên tập hợp Toán lớp 10 hay khác:
(199k) Xem Khóa học Toán 10 CD
Xem thêm tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Lý thuyết Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Cánh diều
- Giải Chuyên đề học tập Toán 10 Cánh diều
- Giải SBT Toán 10 Cánh diều
- Giải lớp 10 Cánh diều (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - Cánh diều
- Soạn văn 10 (ngắn nhất) - Cánh diều
- Soạn văn 10 (siêu ngắn) - Cánh diều
- Giải sgk Toán 10 - Cánh diều
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - Cánh diều
- Giải sgk Hóa học 10 - Cánh diều
- Giải sgk Sinh học 10 - Cánh diều
- Giải sgk Địa lí 10 - Cánh diều
- Giải sgk Lịch sử 10 - Cánh diều
- Giải sgk Kinh tế và Pháp luật 10 - Cánh diều
- Giải sgk Tin học 10 - Cánh diều
- Giải sgk Công nghệ 10 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 10 - Cánh diều
- Giải sgk Giáo dục quốc phòng 10 - Cánh diều









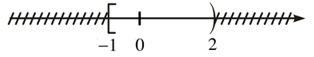
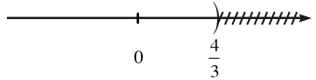







 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

