Hoán vị, chỉnh hợp và tổ hợp lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
Với tóm tắt lý thuyết Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
Hoán vị, chỉnh hợp và tổ hợp lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
(199k) Xem Khóa học Toán 10 CTST
Bài giảng: Bài 2: Hoán vị, chỉnh hợp và tổ hợp - Cô Diệu Minh (Giáo viên VietJack)
Lý thuyết Hoán vị, chỉnh hợp và tổ hợp
1. Hoán vị
– Cho tập hợp A có n phần tử (n ≥ 1).
Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một hoán vị các phần tử đó (gọi tắt là hoán vị của A hay của n phần tử).
Kí hiệu Pn là số hoán vị của n phần tử.
– Số các hoán vị của n phần tử (n ≥ 1) bằng:
Pn = n(n – 1)(n – 2)….2. 1.
Chú ý:
+ Ta đưa vào kí hiệu n! = n(n – 1)(n – 2)…. 2. 1 và đọc là n giai thừa hoặc giai thừa của n.
Khi đó Pn= n!.
+ Quy ước: 0! = 1.
Ví dụ: Có thể lập được bao nhiêu số có 6 chữ số khác nhau từ các chữ số 1; 2; 3; 5; 6; 7? Trong những số đó có bao nhiêu số lẻ?
Hướng dẫn giải
• Mỗi số tự nhiên có 6 chữ số khác nhau được lập từ 6 chữ số 1; 2; 3; 5; 6; 7 là một hoán vị của 6 chữ số này. Do đó, số số tự nhiên có 6 chữ số khác nhau lập được là:
P6 = 6! = 6. 5. 4. 3. 2. 1 = 720 (số).
Vậy lập được 720 số.
Ta lập số tự nhiên lẻ có 6 chữ số khác nhau từ các chữ số 1; 2; 3; 5; 6; 7.
• Bước 1: Chọn chữ số hàng đơn vị là chữ số lẻ.
Có 4 cách chọn (chọn một trong các chữ số 1; 3; 5; 7).
Bước 2: Chọn năm chữ số còn lại.
Có P5 = 5! cách chọn.
Từ đó, theo quy tắc nhân, số số tự nhiên lẻ có sáu chữ số khác nhau lập từ các chữ số đã cho là:
4.5! = 480 (số).
2. Chỉnh hợp
– Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k với 1 ≤ k ≤ n.
Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.
Kí hiệu là số chỉnh hợp chập k của n phần tử.
– Số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) bằng:
= n(n – 1)(n – 2) ….(n – k + 1) = .
Nhận xét: Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó.
Ta có , n ≥ 1.
Ví dụ: Trên bàn có 10 quả cam to nhỏ khác nhau. Chọn 3 quả cam trong 10 quả đó, và đặt mỗi quả vào một giỏ nhựa khác nhau. Hỏi có bao nhiêu cách chọn 3 quả cam đó.
Hướng dẫn giải
Mỗi cách chọn 3 quả cam trong 10 quả cam đó và đặt vào 3 giỏ nhựa được gọi là một chỉnh hợp chập 3 của 10 quả cam. Ta thấy số các chỉnh hợp này bằng:
= 10. 9. 8 = 720.
Vậy có 720 cách chọn 3 quả cam đó.
3. Tổ hợp
– Cho tập hợp A có n phần tử (n ≥ 1).
Mỗi tập con gồm k phần tử (1 ≤ k ≤ n) của A được gọi là một tổ hợp chập k của n phần tử.
Kí hiệu là số tổ hợp chập k của n phần tử (1 ≤ k ≤ n).
– Số các tổ hợp chập k của n phần tử (1 ≤ k ≤ n) bằng:
Chú ý: Người ta quy ước .
Nhận xét: (0 ≤ k ≤ n).
Ví dụ: Lớp 10A có 20 học sinh. Trong tuần sau có 5 bạn được cử đi dự đại hội Đoàn Thanh niên. Hỏi có bao nhiêu cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên?
Hướng dẫn giải
Mỗi cách chọn 5 bạn học sinh trong lớp từ 20 bạn học sinh là một tổ hợp chập 5 của 20 học sinh. Do đó số cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên là:
= 15 504 (cách).
Vậy có 15 504 cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên.
Ví dụ: Tính:
Hướng dẫn giải
4. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay
Với một số máy tính cầm tay, ta có thể tính toán nhanh các số các hoán vị, chỉnh hợp và tổ hợp.
Ví dụ:
• Để tính P10 ta ấn liên tiếp các phím:
Ta nhận được kết quả là 3 628 800.
• Để tính ta ấn liên tiếp các phím:
Ta nhận được kết quả là 360.
• Để tính ta ấn liên tiếp các phím:
Ta nhận được kết quả là 70.
Bài tập Hoán vị, chỉnh hợp và tổ hợp
Bài 1. Có 6 chiếc ghế ở trong một phòng học. Hỏi có 6 học sinh ngồi vào thì có bao nhiêu cách xếp? Nếu có một bạn An (có trong 6 học sinh trên) muốn ngồi vào chiếc ghế ngoài cùng bên trái thì có bao nhiêu cách xếp?
Hướng dẫn giải
• Mỗi cách xếp 6 học sinh vào 6 chiếc ghế là một hoán vị của 6 học sinh. Do đó, số cách sắp xếp 6 học sinh vào 6 chiếc ghế trống là:
P6 = 6! = 720 cách.
Vậy có 720 cách xếp 6 học sinh vào 6 ghế trống.
• Bạn An muốn ngồi vào chiếc ghế ngoài cùng bên trái nên chỉ còn 5 ghế trống và 5 học sinh.
Do đó, số cách xếp 5 học sinh vào 5 chiếc ghế trống là:
P5 = 5! = 120 cách.
Vậy bạn An muốn ngồi vào chiếc ghế bên trái cùng thì có 120 cách xếp.
Bài 2. Trong một đại hội Đoàn gồm có 10 ứng viên. Người ta cần bầu ra một chủ tịch, một phó chủ tịch, một ủy viên và một thư kí. Hỏi có bao nhiêu khả năng có thể về kết quả bầu này?
Hướng dẫn giải
Mỗi cách chọn 4 người trong số 10 ứng viên để vào 4 vị trí (chủ tịch, phó chủ tịch, ủy viên và thư kí) là một chỉnh hợp chập 4 của 10 ứng viên. Do đó có số khả năng có thể về kết quả bầu này là:
= = 5 040.
Vậy có 5 040 khả năng có thể về kết quả bầu.
Bài 3. Chọn ngẫu nhiên 3 số tự nhiên trong tập hợp các số tự nhiên có 2 chữ số chia hết cho 10. Hỏi có bao nhiêu cách chọn 3 số tự nhiên đó.
Hướng dẫn giải
Các số tự nhiên có 2 chữ số chia hết cho 10 là: 10; 20; 30; …; 90.
Do đó có 9 số tự nhiên có 2 chữ số chia hết cho 10.
Mỗi cách chọn 3 số trong 9 số tự nhiên ở trên là một tổ hợp chập 3 của 9 số tự nhiên. Do đó, số cách chọn 3 số trong 9 số này là:
= = 84 cách.
Vậy có 84 cách chọn 3 số tự nhiên trong tập hợp các số tự nhiên có 2 chữ số chia hết cho 10.
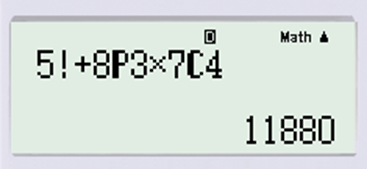
Bài 4. Sử dụng máy tính cầm tay để tính biểu thức sau:
Hướng dẫn giải
Ta ấn lần lượt các phím sau:
5 ; Shift ; ; + ; 8 ; Shift ; × ; 3; × ; 7 ; Shift ; ÷ ; 4; =.
Ta được kết quả là: 11880.
Bài 5. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Có bao nhiêu cách chọn ra 4 viên bi trong mỗi trường hợp sau:
a) 4 viên bi có màu bất kì.
b) 4 viên bi được chọn có đúng hai viên bi màu trắng.
Hướng dẫn giải
a) Có tất cả: 6 + 8 + 10 = 24 viên bi trong hộp.
Chọn ra 4 viên bi trong tổng số 24 viên bi là tổ hợp chập 4 của 24.
Do đó số cách chọn ra 4 viên bi có màu bất kì trong hộp là: (cách).
Vậy có 10 626 cách chọn ra 4 viên bi có màu bất kì.
b) Chọn ra 4 viên bi trong đó có đúng hai viên bi màu trắng ta chia làm hai công đoạn:
Công đoạn 1: chọn ra 2 viên bi màu trắng trong 10 viên bi màu trắng là tổ hợp chập 2 của 10. Do đó có (cách).
Công đoạn 1: chọn ra 2 viên bi trong 14 viên bi còn lại là tổ hợp chập 2 của 14. Do đó có (cách).
Theo quy tắc nhân ta có: 45.91= 4 095 cách chọn ra 4 viên bi trong đó có đúng 2 viên bi màu trắng.
Học tốt Hoán vị, chỉnh hợp và tổ hợp
Các bài học để học tốt Hoán vị, chỉnh hợp và tổ hợp Toán lớp 10 hay khác:
(199k) Xem Khóa học Toán 10 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
- Lý thuyết Toán 10 Bài 3: Nhị thức Newton
- Tổng hợp lý thuyết Toán 10 Chương 8
- Lý thuyết Toán 10 Bài 1: Toạ độ của vectơ
- Lý thuyết Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ
- Lý thuyết Toán 10 Bài 3: Đường tròn trong mặt phẳng toạ độ
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 10 Chân trời sáng tạo
- Giải SBT Toán 10 Chân trời sáng tạo
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - CTST
- Soạn văn 10 (ngắn nhất) - CTST
- Soạn văn 10 (siêu ngắn) - CTST
- Giải Toán 10 - CTST
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - CTST
- Giải sgk Hóa học 10 - CTST
- Giải sgk Sinh học 10 - CTST
- Giải sgk Địa lí 10 - CTST
- Giải sgk Lịch sử 10 - CTST
- Giải sgk Kinh tế và Pháp luật 10 - CTST
- Giải sgk Hoạt động trải nghiệm 10 - CTST

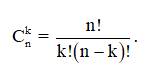
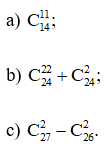
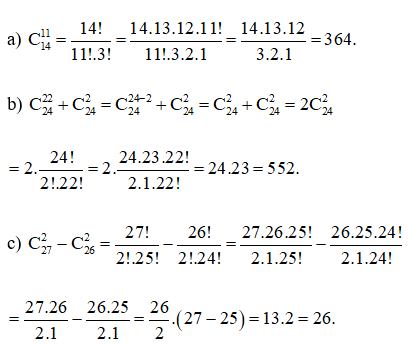
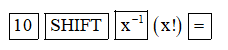
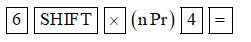




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

