Giải tam giác và ứng dụng thực tế lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
Với tóm tắt lý thuyết Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
Giải tam giác và ứng dụng thực tế lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
(199k) Xem Khóa học Toán 10 CTST
Lý thuyết Giải tam giác và ứng dụng thực tế
1. Giải tam giác
Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.
Ví dụ 1. Giải tam giác ABC biết AB = 45, AC = 32 và 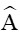
Hướng dẫn giải
+) Theo định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
BC2 = 452 + 322 – 2.45.32.cos60° = 1609.
BC ≈ 40,11.
+) Theo định lí sin ta có:
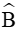
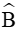
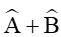
Xét tam giác ABC có 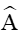
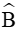
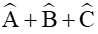
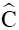
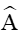
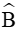
Vậy BC ≈ 40,11; 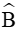
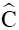
2. Áp dụng giải tam giác vào thực tế
Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
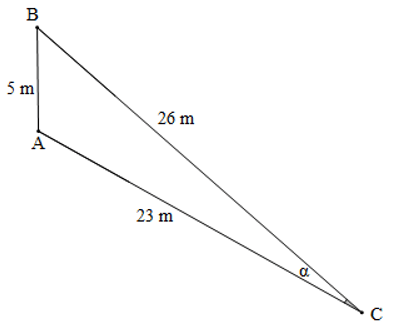
Ví dụ 2. Một khung thành bóng đá rộng 5 mét. Một cầu thủ đứng ở vị trí cách cột dọc khung thành 26 mét và cách cột còn lại 23 mét, sút bóng vào khung thành. Tính góc nhìn của cầu thủ tới hai cột khung thành trên.
Hướng dẫn giải
Vị trí cầu thủ C và khung thành AB được mô tả như hình vẽ dưới đây:
Gọi α là góc nhìn của cầu thủ C tới hai cột khung thành A và B, tức là =
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Suy ra α ≈ 9°23'.
Vậy góc nhìn của cầu thủ tới hai cột khung thành là khoảng 9°23'.
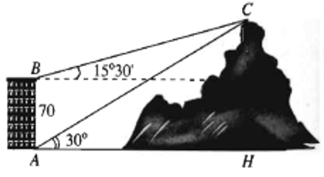
Ví dụ 3.Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ). Tính độ cao của ngọn núi.
Hướng dẫn giải
Ta có 
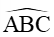
Xét tam giác ABC ta có:
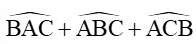


Áp dụng định lí sin ta có:
AC ≈ 269,4 (m)
Tam giác ACH vuông tại H ta có:
CH = AC.sin
Vậy ngọn núi cao khoảng 134,7 m.
Bài tập Giải tam giác và ứng dụng thực tế
1. Bài tập trắc nghiệm
Câu 1. Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:
A. 2
B. 3
C. 4;
D. 5.
Hướng dẫn giải
Đáp án đúng là: D
Diện tích tam giác ABC là: S = .AB.Ac.sinA sinA =
sinA = 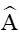
Xét tam giác ABC có AB = 5, AC = 8 và , áp dụng định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
BC2 ≈ 52 + 82 – 2.5.8.cos36°52' ≈ 25
BC ≈ 5.
Vậy BC ≈ 5.
Câu 2. Cho tam giác ABC. Biết AB = 2, BC = 3 và 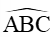
A. 5+ và ;
B. 5+ và ;
C. 5+ và ;
D. 5+ và .
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC có AB = 2, BC = 3 và 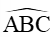
AC2 = AB2 + BC2 – 2.AB.BC. cos
AC2 = 22 + 32 – 2.2.3.cos60° = 7
AC =
Do đó chu vi tam giác ABC là:
AB + AC + BC = 2 +3 + = 5 +
Diện tích tam giác ABC là:
S = .BA.BC.sin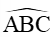
Vậy chu vi và diện tích tam giác ABC lần lượt là: 5 + và
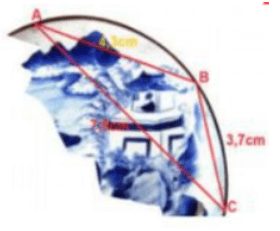
Câu 3. Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
A. 5,73 cm;
B. 6,01 cm;
C. 5,85 cm;
D. 4,57 cm.
Hướng dẫn giải
Đáp án đúng là: A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Nửa chu vi của tam giác ABC là:
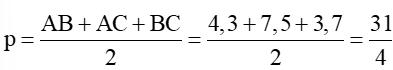
Diện tích tam giác ABC theo công thức Heron là:
Mặt khác:
Vậy bán kính của chiếc đĩa là khoảng 5,73 cm.
2. Bài tập tự luận
Bài 1. Giải tam giác ABC biết AC = 16, 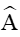
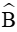
Hướng dẫn giải
Xét tam giác ABC có 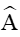
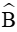
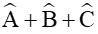
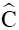
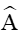
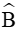
Theo định lí sin ta có:
Vậy 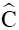
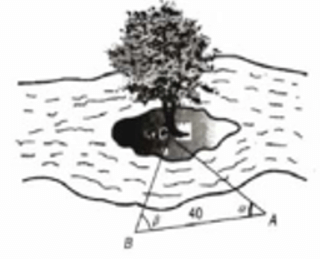
Bài 2. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B đều có thể nhìn thấy điểm C. Người ta đo được khoảng cách AB = 40 m, 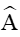
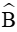
Hướng dẫn giải
Xét tam giác ABC có 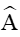
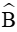
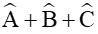
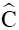
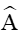
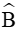
Áp dụng định lí sin vào tam giác ABC ta có:
Vậy khoảng cách từ A trên bờ sông đến gốc cây C khoảng 41,47 m.
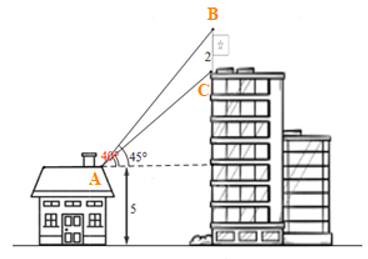
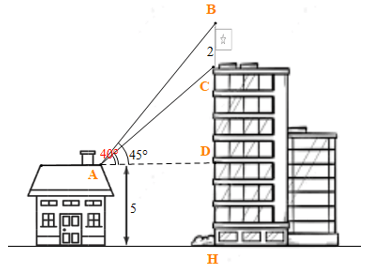
Bài 3. Trên nóc một toà nhà có một cột cờ cao 2 m. Từ vị trí quan sát A cao 5 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột cờ dưới góc 45° và 40° so với phương nằm ngang (hình vẽ). Tìm chiều cao của toà nhà.
Hướng dẫn giải
Từ hình vẽ ta có 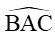
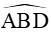
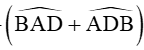
Do đó 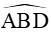
Suy ra: 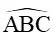
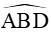
Áp dụng định lí sin trong tam giác ABC có:
Suy ra
Trong tam giác vuông ADC có:
CD = AC.sin
Do đó CH = CD + DH ≈ 10,4 + 5 ≈ 15,4 (m).
Vậy chiều cao của toà nhà là khoảng 15,4 m.
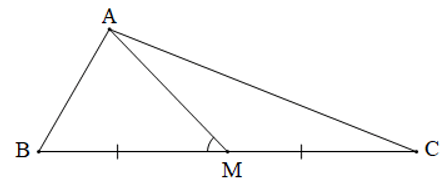
Bài 4. Tam giác ABC có AB = 3, BC = 8, M là trung điểm của BC, 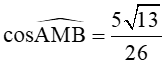
Hướng dẫn giải
Vì M là trung điểm của BC nên BM = MC = BC = .8 = 4.
Xét tam giác ABM, áp dụng hệ quả định lí côsin ta có:
Do đó AM = .
Vì 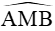
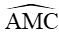
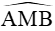
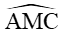
Suy ra cos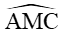
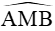
Xét tam giác AMC, áp dụng định lí côsin ta có:
AC2 = AM2 + CM2 - 2.AM.CM.cos
AC2 = ()2 + 42 - 2..4.
AC2 = 49
AC = 7.
Xét tam giác ABM có AB = 3, BM = 4, AM = áp dụng định lí côsin ta có:
Xét tam giác ABC, áp dụng định lí sin ta có:
Mà tam giác ABC là tam giác tù nên 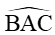
Xét tam giác ABC ta có:
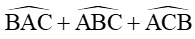


Vậy AM = , AC = 7, 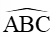
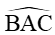

Học tốt Giải tam giác và ứng dụng thực tế
Các bài học để học tốt Giải tam giác và ứng dụng thực tế Toán lớp 10 hay khác:
(199k) Xem Khóa học Toán 10 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 10 Chân trời sáng tạo
- Giải SBT Toán 10 Chân trời sáng tạo
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - CTST
- Soạn văn 10 (ngắn nhất) - CTST
- Soạn văn 10 (siêu ngắn) - CTST
- Giải Toán 10 - CTST
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - CTST
- Giải sgk Hóa học 10 - CTST
- Giải sgk Sinh học 10 - CTST
- Giải sgk Địa lí 10 - CTST
- Giải sgk Lịch sử 10 - CTST
- Giải sgk Kinh tế và Pháp luật 10 - CTST
- Giải sgk Hoạt động trải nghiệm 10 - CTST


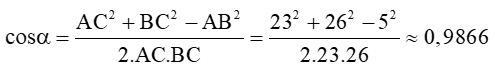
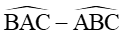
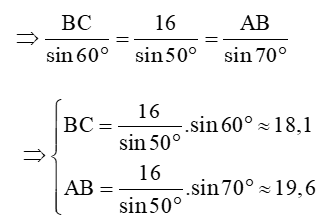
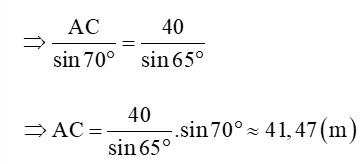
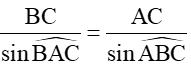
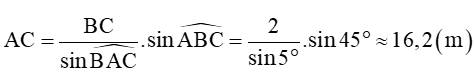
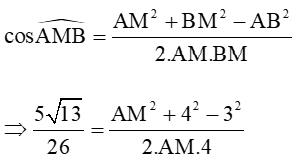
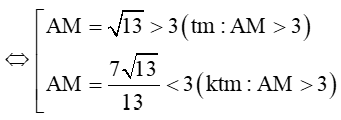
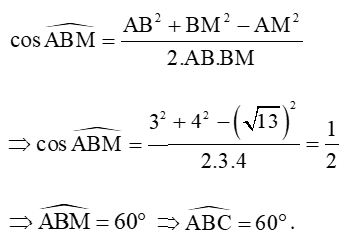
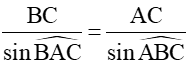
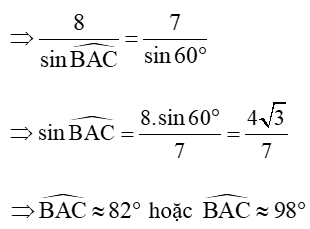
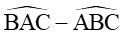



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

