Giá trị lượng giác của một góc từ 0° đến 180° lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
Với tóm tắt lý thuyết Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180° sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
Giá trị lượng giác của một góc từ 0° đến 180° lớp 10 (Lý thuyết Toán 10 Chân trời sáng tạo)
(199k) Xem Khóa học Toán 10 CTST
Bài giảng: Bài 1: Giá trị lượng giác của một góc từ 0° đến 180° - Cô Mai Ngọc Hà (Giáo viên VietJack)
Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180°
1. Giá trị lượng giác
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho 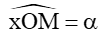
– Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0;
– Hoành độ x0 của M là côsin của góc α, kí hiệu là cosα = x0;
– Tỉ số (x0 ≠ 0) là tang của góc α, kí hiệu là tanα =
–Tỉ số (y0 ≠ 0) là côtang của góc α, kí hiệu là cotα =
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.
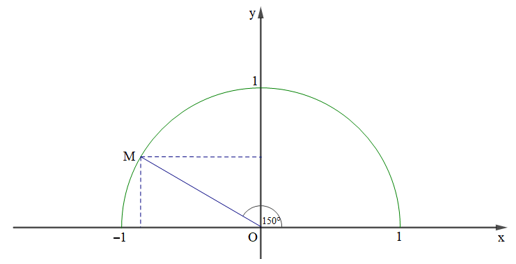
Ví dụ 1. Tìm các giá trị lượng giác của góc 150°.
Hướng dẫn giải
Lấy điểm M trên nửa đường tròn đơn vị sao cho 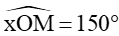
Ta có: 
Khi đó ta tính được toạ độ của điểm M là
Theo định nghĩa ta có:
sin150o = ; cos150o = ; tan150o = ; cot150o = -.
Chú ý:
a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.
Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
b) tanα chỉ xác định khi α ≠ 90°.
cotα chỉ xác định khi α ≠ 0° và α ≠ 180°.
Ví dụ 2. Với α = 30° thì sinα > 0, cosα > 0, tanα > 0 và cotα > 0.
Với α = 150° (như trong Ví dụ 1) thì sinα > 0, cosα < 0, tanα < 0 và cotα < 0.
2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
– Từ lớp dưới ta đã biết hai góc phụ nhau thì các tỉ số lượng giác của chúng có mối liên hệ:
sin(90° – α) = cosα;
cos(90° – α) = sinα;
tan(90° – α) = cotα;
cot(90° – α) = tanα.
– Mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Ví dụ 3.
a) Biết sin60o=. Tính cos30°, cos150°, sin120°.
b) Biết tan45° = 1. Tính tan135°.
Hướng dẫn giải
a) Ta có: sin60o=
Suy ra:
cos30° = cos(90° – 60°) = sin 60° = (vì 30° và 60° là hai góc phụ nhau);
cos150° = cos(180° – 30°) = –cos30° = - (vì 150° và 30° là hai góc bù nhau);
sin120° = sin(180° – 60°) = sin60° = (vì 120° và 60° là hai góc bù nhau);
b) Ta có: tan45° = 1.
Suy ra:
tan135° = tan(180° ‒ 45°) = ‒tan45° = ‒1 (vì 135° và 45° là hai góc bù nhau).
3. Giá trị lượng giác của một số góc đặc biệt
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt:

Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Ví dụ 4. Tính giá trị các biểu thức sau:
a) A = a2.sin90° + b2.cos90° + c2.cos180°;
b) B = 3 – sin2 135° + 2cos2 120° ‒ 3tan2 150°.
Hướng dẫn giải
a) A = a2.sin90° + b2.cos90° + c2.cos180°
A = a2. 1 + b2.0 + c2.(‒1)
A = a2 ‒ c2.
b) B = 3 – sin2 135° + 2cos2 120° ‒ 3tan2 150°
B = 3 - + 2. - 3.
B = 3 - + 2. - 3.
B = 3 - + - 1
B = 2.
Ví dụ 5. Tìm góc α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) sinα = ;
b) cosα = ‒1;
c) tanα = 0;
d) cotα = -.
Hướng dẫn giải
a) Ta có: sinα = α = 45° hoặc α = 135°.
b) cosα = ‒1 α = 180°.
c) tanα = 0 α = 0° hoặc α = 180°.
d) cotα = - α = 120°.
4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
Có nhiều loại máy tính cầm tay có thể giúp tính nhanh chóng giá trị lượng giác của một góc.
Chẳng hạn, ta có thể thực hiện trên máy tính cầm tay vinacal 680EX PLUS như sau:
Sau khi mở máy, ẩn liên tiếp các phím 
Ấn phím 
Ấn tiếp phím 
Ấn các phím 
4.1. Tính các giá trị lượng giác của góc
Ví dụ 6. Sử dụng máy tính cầm tay, tính sin125°, cos50°12', tan160°56'25'', cot100°.
Hướng dẫn giải
– Để tính sin125°, ta bấm liên tiếp các phím sau đây: 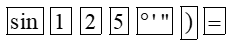
Khi đó ta được kết quả hiện trên màn hình là:
Vậy sin125° ≈ 0,8191520443.
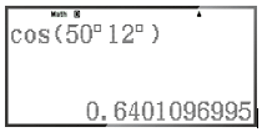
– Để tính cos50°12', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cos50°12' ≈ 0,6401096995.
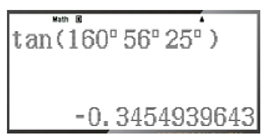
– Để tính tan160°56'25'', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy tan160°56'25'' ≈ ‒0,34549339643.
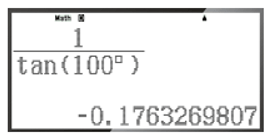
– Để tính cot100°, ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cot100° ≈ ‒0,1763269807.
4.2. Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Ví dụ 7. Sử dụng máy tính cầm tay, tìm α (0° < α < 180°) biết sinα = 0,51; cosα = ‒0,7; tanα = ; cotα = 1,7.
Hướng dẫn giải
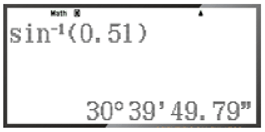
– Để tìm α khi biết sinα = 0,51, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với sinα = 0,51 thì α ≈ 30°39'50''.
Ta đã được học với 0° < α < 180° thì sin(180° ‒ α) = sinα nên ngoài giá trị α ≈ 30°39'50'' thì ta còn có giá trị α ≈ 180° ‒ 30°39'50'' ≈ 149°20'10''.
Ta bấm máy tính như sau:
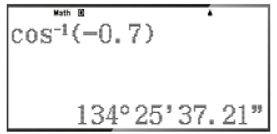
– Để tìm α khi biết cosα = ‒0,7, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cosα = ‒0,7 thì α ≈ 134°25'37''.
– Để tìm α khi biết tanα = ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với tanα = thì α ≈ 54°44'8''.
– Để tìm α khi biết cotα = 1,7, trước hết ta tính , ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Sau đó ta bấm liên tiếp các phím:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cotα = 1,7 thì α ≈ 30°27'56''.
Bài tập Giá trị lượng giác của một góc từ 0° đến 180°
1. Bài tập trắc nghiệm
Câu 1. Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
A. ‒1;
B. 0;
C. 1;
D. 2.
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC ta có: 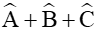
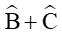
cos(B + C) = cos(180° ‒ A) = ‒cosA;
Và sin(B + C) = sin(180° ‒ A) = sinA.
Do đó:
sinA.cos(B + C) + cosA.sin(B + C)
= sinA.(‒cosA) + cosA.sinA
= ‒sinA.cosA + cosA.sinA
= 0
Vậy sinA.cos(B + C) + cosA.sin(B + C) = 0.
Câu 2. Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của là
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: D
Vì tanα = ‒3 nên = -3 do đó cosα ≠ 0
Ta có:
(do cosα ≠ 0)
Vậy
Câu 3. Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 180°, giá trị của biểu thức: M = cosα.cosβ – sinβ.sinα là:
A. M = ‒1;
B. M = 2;
C. M = 0;
D. M = 1.
Hướng dẫn giải
Đáp án đúng là: A
Vì hai góc α và β (0° ≤ α, β ≤ 180°) là hai góc bù nhau (do α + β = 180°) nên:
cosβ = ‒cosα và sinβ = sinα.
Ta có: M = cosα.cosβ – sinβ.sinα
M = cosα.(‒cosα) ‒ sinα.sinα = ‒cos2α ‒ sin2α
M = ‒(cos2α + sin2α)
Mà cos2α + sin2α = 1 (đã được chứng minh ở bài 5, trang 65, Sách giáo khoa Toán 10, Tập một).
Vậy M = ‒1.
2. Bài tập tự luận
Bài 1. Tính giá trị biểu thức:
a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°.
b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°;
c) C = sin(180o-x) - cos(90o-x) + sin2x.- tan2x
Hướng dẫn giải
a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°
b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°
B = (cos0° + cos180°) + (cos20° + cos160°) + … + (cos80° + cos100°)
B = (cos0° ‒ cos0°) + (cos20° ‒ cos20°) + … + (cos80° ‒ cos80°) (hai góc bù nhau)
B = 0.
c) C = sin(180o-x) - cos(90o-x) + sin2x.- tan2x
C = sinx - sinx + sin2x. - tan2x
C = 0 + tan2x ‒ tan2x
C = 0.
Bài 2. Cho góc α (0° ≤ α ≤ 180°) với tanα = -. Tính giá trị biểu thức:
M = cosα + cot2α -
Hướng dẫn giải
Với tanα = - ta có α = 120°.
Suy ra: sinα = ; cosα = -; cotα = -.
Do đó:
M = cosα + cot2α -
Vậy
Bài 3. Sử dụng máy tính cầm tay để thực hiện các yêu cầu sau:
a) Tính sin95°7'16'', cos22°12'21'', tan27°22', cot24°.
b) Tìm β biết (0° < β < 180°) trong các trường hợp:
i) cosβ = ‒0,19;
ii) tanβ = 1,2.
Hướng dẫn giải
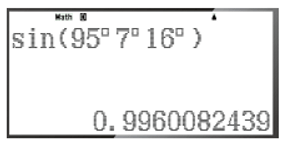
a) – Để tính sin95°7'16'', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy sin95°7'16'' ≈ 0,9960082439.
– Để tính cos22°12'21'', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cos22°12'21'' ≈ 0,9258321117.
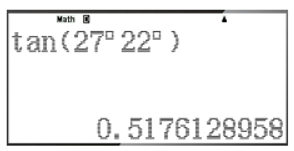
– Để tính tan27°22', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy tan27°22' ≈ 0,5176128958.
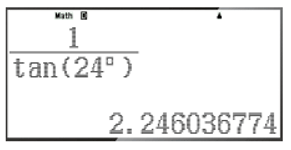
– Để tính cot24°, ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cot24° ≈ 2,246036774.
b) – Để tìm β khi biết cosβ = ‒0,19, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cosβ = ‒0,19 thì β ≈ 100°57'10''.
– Để tìm β khi biết tanβ = 1,2, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với tanβ = 1,2 thì β ≈ 50°11'40''.
Học tốt Giá trị lượng giác của một góc từ 0° đến 180°
Các bài học để học tốt Giá trị lượng giác của một góc từ 0° đến 180° Toán lớp 10 hay khác:
(199k) Xem Khóa học Toán 10 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 10 Chân trời sáng tạo
- Giải SBT Toán 10 Chân trời sáng tạo
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - CTST
- Soạn văn 10 (ngắn nhất) - CTST
- Soạn văn 10 (siêu ngắn) - CTST
- Giải Toán 10 - CTST
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - CTST
- Giải sgk Hóa học 10 - CTST
- Giải sgk Sinh học 10 - CTST
- Giải sgk Địa lí 10 - CTST
- Giải sgk Lịch sử 10 - CTST
- Giải sgk Kinh tế và Pháp luật 10 - CTST
- Giải sgk Hoạt động trải nghiệm 10 - CTST











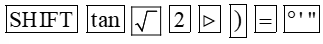

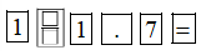

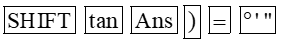





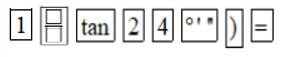
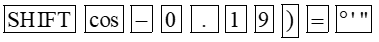

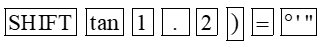




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

