Tổng hợp lý thuyết Toán lớp 6 Chương 1 Kết nối tri thức

Với tóm tắt lý thuyết Toán lớp 6 Chương 1: Tập hợp các số tự nhiên hay nhất, chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.

Tổng hợp lý thuyết Toán lớp 6 Chương 1 Kết nối tri thức

Tổng hợp lý thuyết Toán lớp 6 Chương 1

I. Tập hợp

1. Tập hợp và phần tử của tập hợp 

Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).

Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …

2. Mô tả một tập hợp

2.1. Liệt kê các phần tử của tập hợp

Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.

2.1. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp

Gọi x là phần tử của tập hợp, tìm các tính chất đặc trưng của các phần tử.

II. Cách ghi số tự nhiên

1. Hệ thập phân

Cách ghi số tự nhiên trong hệ thập phân

- Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.

- Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …

Chú ý: Khi viết các số tự nhiên ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.

2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.

Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó.

2. Số La Mã

Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).

Ba chữ số đó cộng với hai cụm chữ số là IV và Ĩ là năm thành phần dùng để ghi số La Mã. 

Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:

Thành phần	I	V	X	IV	IX
Giá trị (viết trong hệ thập phân)	1	5	10	4	9

+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:

+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:

+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:

XXI	XXII	XXIII	XXIV	XXV	XXVI	XXVII	XXVIII	XXIX	XXX
21	22	23	24	25	26	27	28	29	30

III. Thứ tự trong tập hợp các số tự nhiên

Ta đã biết tập các số tự nhiên được kí hiệu là N, nghĩa là N = . Mỗi phần tử 0; 1; 2; 3; … được biểu diễn bởi một điểm trên tia số gốc 0 như hình vẽ:

Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì trên tia số nằm ngang điểm a nằm bên trái điểm b. Khi đó, ta viết a < b hoặc b > a. Ta còn nói: điểm a nằm trước điểm b, hoặc điểm b nằm sau điểm a.

Mỗi số tự nhiên có đúng một số liền sau, chẳng hạn 9 là số liền sau của 8 (còn 8 là số liền trước của 9). Hai số 8 và 9 là hai số tự nhiên liên tiếp.

Nếu a < b và b < c thì a < c (tính chất bắc cầu). Chẳng hạn a < 5 và 5 < 7 suy ra a < 7.

Kí hiệu ≤ và ≥

Ta còn dùng kí hiệu a ≤ b (đọc là “a nhỏ hơn hoặc bằng b”) để nói “a < b hoặc a = b”.

Ta còn dùng kí hiệu a ≥ b (đọc là “a lớn hơn hoặc bằng b”) để nói “a > b hoặc a = b”.

Tính chất bắc cầu còn có thể viết: nếu a ≤ b và b ≤ c thì a ≤ c .

IV. Phép cộng và phép trừ số tự nhiên

1. Phép cộng số tự nhiên

Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.

Có thể minh họa phép cộng nhờ tia số, chẳng hạn phép cộng 3 + 4 = 7

Phép cộng số tự nhiên có các tính chất:

Giáo hoán: a + b = b + a.

Kết hợp: (a + b) + c = a + (b + c).

Chú ý: a + 0  = 0 + a = a.

Tổng (a + b) + c hay a + (b + c) gọi là tổng của ba số a, b, c và viết gọn là: a + b + c.

2. Phép trừ số tự nhiên

Với hai số tự nhiên a, b đã cho, nếu có số tự nhiên c sao cho a + b = c thì ta có phép trừ 

a – b = c.

Trong đó, a là số bị trừ, b là số trừ và c là hiệu.

V. Phép nhân và phép chia số tự nhiên

Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích. Kí hiệu: a.b = c (hoặc a x b = c)

Trong đó: a và b là hai thừa số, c là tích.

Chú ý nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …

VI. Lũy thừa với số mũ tự nhiên

Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a: 

aⁿ = 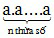(n ∈ N^*)

aⁿ đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.

Chú ý: Ta có a¹ = a.

a² cũng được gọi là a bình phương (hay bình phương của a);

a³ cũng được gọi là a lập phương (hay lập phương của a).

VII. Thứ tự thực hiện các phép tính

Đối với các biểu thức không có dấu ngoặc: 

- Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.

- Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

Đối với các biểu thức có dấu ngoặc: 

- Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.

- Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.

Bài tập tổng hợp Toán lớp 6 Chương 1

Bài 1. Viết số tự nhiên a sau đây: Một tỉ hai trăm năm mươi triệu một trăm linh tám nghìn chin trăm sáu mươi mốt.

a) Số a có bao nhiêu chữ số? Viết tập hợp các chữ số của a;

b) Số chục triệu của a là bao nhiêu?

c) Trong a có hai chữ số 1 nằm ở những hàng nào? Mỗi chữ số ấy có giá trị bằng bao nhiêu?

Lời giải

Số a là: 1 250 108 961.

a) Số a có tất cả 10 chữ số.

Các chữ số có mặt trong số a là: 1; 2; 5; 0; 1; 0; 8; 9; 6; 1.

Gọi A là tập hợp các chữ số của a. Do trong tập hợp các phần tử chỉ được xuất hiện 1 lần nên A = .

b) Số chục triệu của a là: 1 250 000 000.

c) Trong a có hai chữ số 1:

+ Một chữ số 1 nằm ở hàng tỉ và nó có giá trị 1.1 000 000 000 = 1 000 000 000.

+ Số 1 còn lại nằm ở hàng đơn vị và nó có giá trị: 1.1 = 1.

Bài 2. Thực hiện phép tính:

a) 128:4 + 3.(50 – 14);

b) 23.45 + 23.54 + 23;

c) 21:[(1 245 + 987):2³ – 15.12]+21

Lời giải

a) 128:4 + 3.(50 – 14)

= 32 + 3.36

= 32 + 108

= 140.

b) 23.45 + 23.54 + 23

= 23.(45 + 54 + 1)

= 23.100

= 2 300.

c) 21.[(1 245 + 987):2³ – 15.12] + 21

= 21.[2232:8 – 180] + 21

= 21.[279 – 180] + 21

= 21.99 + 21

= 21(99 + 1)

= 21.100

= 2 100.

Bài 3. Một trường cho 480 học sinh khối 6 đi tham quan cùng với đó là 50 thầy cô và phụ huynh học sinh đi để quản lớp. Hỏi trường cần thuê ít nhất bao nhiêu xe 45 chỗ ngồi để đủ chỗ cho tất cả học sinh, thầy cô và phụ huynh.

Lời giải

Có tất cả số người đi tham quan là: 480 + 50 = 530 (người).

Ta có: 530: 45 = 11 (dư 35)

Nghĩa là cần ít nhất 12 xe 45 chỗ ngỗi để đủ chỗ ngồi cho tất cả học sinh, thầy cô và phụ huynh.

Vậy cần ít nhất 12 xe 45 chỗ ngồ để đủ chỗ ngồi cho tất cả học sinh, thầy cô và phụ huynh.

Học tốt Toán lớp 6 Chương 1

Các bài học để học tốt Toán lớp 6 Chương 1 hay khác:

• Giải sgk Toán 6 Bài tổng hợp Chương 1

• Giải sbt Toán 6 Bài tổng hợp Chương 1

Xem thêm tóm tắt lý thuyết Toán lớp 6 Kết nối tri thức với cuộc sống hay, chi tiết khác:

• Lý thuyết Toán 6 Bài 8: Quan hệ chia hết và tính chất

• Lý thuyết Toán 6 Bài 9: Dấu hiệu chia hết

• Lý thuyết Toán 6 Bài 10: Số nguyên tố

• Lý thuyết Toán 6 Bài 11: Ước chung. Ước chung lớn nhất

• Lý thuyết Toán 6 Bài 12: Bội chung. Bội chung nhỏ nhất

Xem thêm các tài liệu học tốt lớp 6 hay khác:

• Giải sgk Toán 6 Kết nối tri thức
• Giải SBT Toán 6 Kết nối tri thức
• Giải lớp 6 Kết nối tri thức (các môn học)
• Giải lớp 6 Chân trời sáng tạo (các môn học)
• Giải lớp 6 Cánh diều (các môn học)

---