Bội chung. Bội chung nhỏ nhất (Lý thuyết Toán lớp 6) | Kết nối tri thức

Với tóm tắt lý thuyết Toán lớp 6 Bài 12: Bội chung. Bội chung nhỏ nhất hay nhất, chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.

Bội chung. Bội chung nhỏ nhất (Lý thuyết Toán lớp 6) | Kết nối tri thức

Lý thuyết Bội chung. Bội chung nhỏ nhất

1. Bội chung và bội chung nhỏ nhất

Bội chung của hai hay nhiều số là bội của tất cả các số đã cho.

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu:

BC(a, b) là tập hợp các bội chung của a và b.

BCNN(a, b) là bội chung nhỏ nhất của a và b.

Ví dụ 1. Tìm bội chung và bội chung nhỏ nhất của 30 và 45

Lời giải 

Ta có B(30) = {0; 30; 60; 90; 120; 150; 180; 210; 240; 270; …}

B(45) = {0; 45; 90; 135; 180; 225; 270; …}

BC(30, 45) = {0; 90; 180; 270; …}.

BCNN(30, 45) = 90.

Nhận xét: Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất đó. 

Nếu a 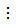b thì BCNN(a, b) = a.

Mọi số tự nhiên đều là bội của 1. Do đó với mọi số tự nhiên a và b (khác 0), ta có: 

BCNN(a, 1) = a; BCNN(a, b, 1) = BCNN(a, b).

Ví dụ 2. Tìm bội chung nhỏ nhất của các số sau:

a) 12 và 36;

b) 124 và 1.

Lời giải

a) Vì 36 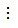12 nên BCNN(12, 36) = 36;

b) Vì 124 là bội của 1 nên BCNN(1; 124) = 124.

2. Cách tìm bội chung nhỏ nhất

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

Bước 1. Phân tích mỗi số ra thừa số nguyên tố;

Bước 2. Chọn ra các thừa số nguyên tố chung và riêng;

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Ví dụ 3. Tìm bội chung nhỏ nhất của 21 và 14.

Lời giải

Ta có 21 = 3.7; 14 = 2.7.

Khi đó BCNN(21, 14) = 2.3.7 = 42.

Tìm bội chung từ bội chung nhỏ nhất

Để tìm bội chung của các số đã cho ta có thể làm như sau:

Bước 1. Tìm BCNN của các số đã cho.

Bước 2. Tìm các bội của BCNN đó.

Ví dụ 4. Tìm BC(12, 24, 30) 

Lời giải

Ta có: 12 = 2².3; 24 = 2³.3; 30 = 2.3.5.

BCNN(12, 24, 30) = 2³.3.5 = 120.

BC(12, 24, 30) = B(120) = {0; 120; 240; 360; 480; …}.

3. Quy đồng mẫu các phân số

Vận dụng BCNN để tìm mẫu chung của hai phân số:

Để quy đồng mẫu số hai phân số 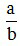  và 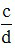 , ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là BCNN của hai mẫu.

Ví dụ 5. Quy đồng mẫu số các phân số sau:

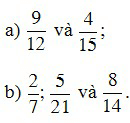
Lời giải

a) Ta có 12 = 2².3; 15 = 3.5.

BCNN(12, 15) = 2².3.5 = 60.

Ta có: 60:12 = 5; 60:15 = 4. Khi đó:

 

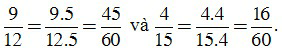
b) Ta có: 7 = 7, 21 = 3. 7, 14 = 2.7.

BCNN(7, 21, 14) = 2.3.7 = 42.

Ta có: 42:7 = 6, 42:21 = 2, 42:14 = 3. Khi đó:

 

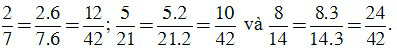
Bài tập Bội chung. Bội chung nhỏ nhất

Bài 1. Tìm BCNN của các số sau:

a) 27 và 36;

b) 49 và 14.

Lời giải

a) Ta có: 27 = 3³, 36 = 2².3².

Khi đó BCNN(27, 36) = 3³.2² = 27.4 = 108.

Vậy BCNN(27, 36) = 108.

b) Ta có 49 = 7², 14 = 2.7.

Khi đó BCNN(49, 14) = 7².2 = 49.2 = 98.

Vậy BCNN(49, 14) = 98.

Bài 2. Học sinh lớp 6A và 6B khi xếp thành 3 hàng, 5 hàng hay 6 hàng đều vừa đủ. Biết số học sinh của hai lớp từ 70 đến 100 học sinh. Tính số học sinh của lớp 6A và 6B.

Lời giải

Vì số học sinh của lớp 6A và 6B xếp thành 3 hàng, 5 thàng hay 6 hàng đều vừa đủ nghĩa là số học sinh của hai lớp 6A và 6B chia hết cho 3 , 5 và 6 hay số học sinh của lớp 6A và 6B là bội chung của 3, 5 và 6.

Ta có: 3 = 3, 6 = 2.3, 5 = 5.

BCNN(3, 5, 6) = 2.3.5 = 30.

BC(3, 5, 6) = B(30) = {0; 30; 60; 90; 120; …}.

Suy ra x ∈ {0; 30; 60; 90; 120; …}.

Biết số học sinh của hai lớp từ 70 đến 100 học sinh nên số học sinh hai lớp là 90.

Vậy số học sinh của hai lớp 6A và 6B là 90 học sinh.

Bài 3. Thực hiện phép tính:

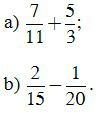
Lời giải

a)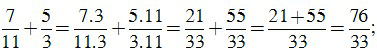  

b)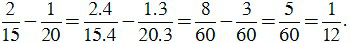  

Học tốt Bội chung. Bội chung nhỏ nhất

Các bài học để học tốt Bội chung. Bội chung nhỏ nhất Toán lớp 6 hay khác:

• Giải sgk Toán 6 Bài 12: Bội chung. Bội chung nhỏ nhất

• Giải sbt Toán 6 Bài 12: Bội chung. Bội chung nhỏ nhất

Xem thêm tóm tắt lý thuyết Toán lớp 6 Kết nối tri thức với cuộc sống hay, chi tiết khác:

• Tổng hợp lý thuyết Toán lớp 6 Chương 2

• Lý thuyết Toán 6 Bài 13: Tập hợp các số nguyên

• Lý thuyết Toán 6 Bài 14: Phép cộng và phép trừ số nguyên

• Lý thuyết Toán 6 Bài 15: Quy tắc dấu ngoặc

• Lý thuyết Toán 6 Bài 16: Phép nhân số nguyên

Xem thêm các tài liệu học tốt lớp 6 hay khác:

• Giải sgk Toán 6 Kết nối tri thức
• Giải SBT Toán 6 Kết nối tri thức
• Giải lớp 6 Kết nối tri thức (các môn học)
• Giải lớp 6 Chân trời sáng tạo (các môn học)
• Giải lớp 6 Cánh diều (các môn học)

---