Công thức giải nhanh Toán 12 Giải tích chi tiết nhất
Tóm tắt Công thức giải nhanh Toán 12 Giải tích chi tiết nhất chương trình sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều. Hi vọng loạt bài này sẽ như là cuốn sổ tay công thức giúp bạn học tốt môn Toán 12 hơn.
Công thức giải nhanh Toán 12 Giải tích chi tiết nhất
Chủ đề: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Chủ đề: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
Công thức tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
Công thức tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
Chủ đề: Nguyên hàm. Tích phân
Lưu trữ: Công thức Toán 12 Giải tích (sách cũ)
Công thức giải nhanh Toán lớp 12 Chương 1 Giải tích chi tiết nhất
Công thức giải nhanh Toán lớp 12 Chương 2 Giải tích chi tiết nhất
Công thức giải nhanh Toán lớp 12 Chương 3 Giải tích chi tiết nhất
Công thức giải nhanh Toán lớp 12 Chương 4 Giải tích chi tiết nhất
Công thức giải nhanh Toán lớp 12 Chương 1 Giải tích chi tiết nhất
1. Các bước chung khảo sát sự biến thiên và vẽ đồ thị hàm số:(6 dấu +)
+ Tập xác định:
+ Giới hạn (và tiệm cận đối với hàm phân thức 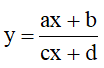
+ Đạo hàm:
- Đối với hàm bậc 3, bậc 4: Giải phương trình tìm nghiệm.
- Đối với hàm phân thức 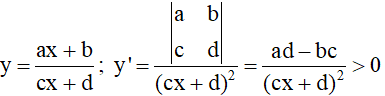
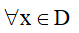
+ Bảng biến thiên:
Nhận xét về chiều biến thiên và cực trị.
+ Bảng giá trị: (5 điểm đối với hàm bậc 3, bậc 4; 6 điểm đối với hàm phân thức 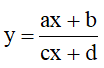
+ Vẽ đồ thị:
2. Tìm điều kiện của tham số m để hàm số đơn điệu trên từng khoảng xác định:
a. Hàm bậc 3: y = ax3 + bx2 + cx + d
Tập xác định 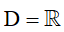
Đạo hàm y' = ax2 + 2bx + c là 1 tam thức bậc 2.
- Hàm số đồng biến trên 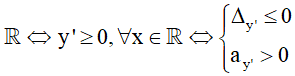
- Hàm số nghịch biến trên 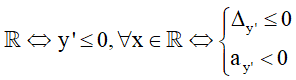
b. Hàm nhất biến:
Tập xác định
Đạo hàm 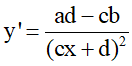
- Hàm số đồng biến trên từng khoảng xác định
⇔ y' > 0, ∀x ∈ D ⇔ ad - cb > 0 (Không có dấu “=”)
- Hàm số nghịch biến trên từng khoảng xác định
⇔ y' < 0, ∀x ∈ D ⇔ ad - cb < 0 (Không có dấu “=”)
. Cực trị của hàm số:
- Hàm số y = f(x) đạt cực trị tại 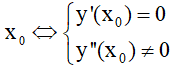
- Hàm số y = f(x) đạt cực đại tại
- Hàm số y = f(x) đạt cực tiểu tại
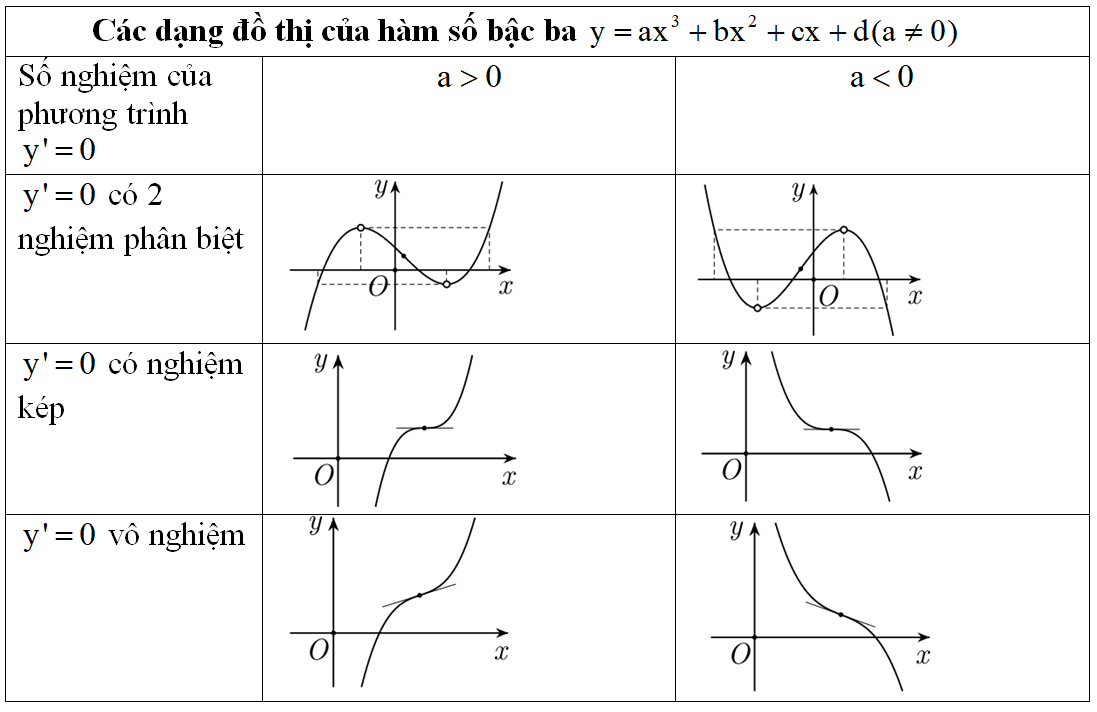
a. Hàm bậc 3: y = ax3 + bx2 + cx + d (a ≠ 0)
⇒ y' = ax2 + 2bx + c
- Hàm số có 2 cực trị (cực đại và cực tiểu) ⇔ phương trình y = 0 có 2 nghiệm phân biệt
- Hàm số không có cực trị ⇔ Phương trình y = 0 vô nghiệm hoặc có nghiệm kép
b. Hàm bậc 4 (trùng phương): y = ax4 + bx2 + c (a ≠ 0)
⇒ y' = 4ax3 + 2bx + c
Ta có: y' = 0 ⇔ y' = 4ax3 + 2bx + c
- Hàm số có 3 cực trị ⇔ Phương trình ⇔ có 3 nghiệm phân biệt
⇔ Phương trình (2) có 2 nghiệm phân biệt khác 0 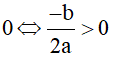
- Hàm số có 1 cực trị ⇔ Phương trình ⇔ có 1 nghiệm
⇔ Phương trình (2) vô nghiệm hoặc có nghiệm kép bằng 0 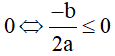
4. Phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) xác định trên 1 đoạn [a;b]
- Hàm số liên tục trên đoạn [a;b]
- Tính đạo hàm .
Giải phương trình y = 0 . Tìm các nghiệm xi ∈ [a;b] (i = 1,2,3....)
- Tính y(a) , y(b) , y(xi)
- So sánh và kết luận.
b. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên 1 khoảng hoặc nửa khoảng (a;b),(a;+∞),(-∞;b),[a;b),(a;b] …
- Tìm tập xác định.
- Tính đạo hàm
- Lập bảng biến thiên
- Dựa vào bảng biến thiên, so sánh và kết luận.
5. Tìm giao điểm của hai đường.
- Cho hai đồ thị (C1): y = f1(x) và (C2): y = f2(x) .
- Phương trình hoành độ giao điểm của (C1) và (C2) là : f1(x) = f2x (*)
- Giải phương trình (*) ta được hoành độ giao điểm, thế vào 1 trong 2 hàm số y = f1(x) hoặc y = f2(x) được tung độ giao điểm.
6. Tìm điều kiện của tham số m để hai đường cong cắt nhau với số điểm cho trước.
- Cho hai đồ thị (C1): y = f1(x) và (C2): y = f2(x) .
- Phương trình hoành độ giao điểm của (C1) và (C2) là : f1(x) = f2x (*)
- (C1) và (C2) cắt nhau tại n điểm phân biệt khi và chỉ khi phương trình (*) có n nghiệm phân biệt.
Lưu ý : Trục hoành có phương trình
7. Dùng đồ thị biện luận theo tham số m số nghiệm của phương trình.
Cho đồ thị (C) : y = f(x) . Dùng đồ thị (C), biện luận theo m số nghiệm của phương trình .
Biến đổi phương trình h(x,m) = 0 về dạng f(x) = g(m) (*).
- Số nghiệm của phương trình (*) là số giao điểm của hai đồ thị :
- Bảng kết quả :
Lưu ý: Nếu bài toán chỉ yêu cầu tìm các giá trị của m để phương trình có đúng 3 nghiệm, 4 nghiệm,… ta không cần lập bảng kết quả như trên mà chỉ cần chỉ rõ các trường hợp thỏa đề (Dựa vào đồ thị ta thấy (C) và (d) cắt nhau tại đúng 3 điểm, đúng 4 điểm …)
8. Viết phương trình tiếp tuyến của đồ thị hàm số:
Cho hàm số y = f(x) có đồ thị là đường cong (C). Phương trình tiếp tuyến của đồ thị tại điểm M0(x0; y0) là: y = f'(x0)(x - x0) + y0
Lưu ý: Ta phải tìm được 3 đại lượng: 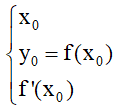
Dạng 1: Viết phương trình tiếp tuyến khi biết hoành độ tiếp điểm
- Tính đạo hàm y'
- Thay x0 vào y tính y0
- Thay x0 vào y tính f'(x0)
- Phương trình tiếp tuyến: y = f'(x0)(x - x0) + y0
Dạng 2: Viết phương tiếp tuyến khi biết tung độ tiếp điểm y0 .
- Giải phương trình f(x0) = y0 tìm x0 .
- Thay x0 vào y tính f'(x0)
- Phương trình tiếp tuyến: y = f'(x0)(x - x0) + y0
Dạng 3: Viết phương trình tiếp tuyến khi biết hệ số góc k .
- Giả sử tiếp điểm là M0(x0; y0)
- Giải phương trình f'(x0) = k tìm x0 .
- Thay x0 vào y ta tìm được y0 .
- Phương trình tiếp tuyến: y = f'(x0)(x - x0) + y0
Lưu ý:
- Nếu tiếp tuyến song song với đường thẳng y = ax + b thì f'(x0) = a .
- Nếu tiếp tuyến vuông góc với đường thẳng y = ax + b (a ≠ 0) thì 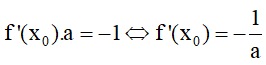
Công thức giải nhanh Toán lớp 12 Chương 2 Giải tích chi tiết nhất
I. Lũy thừa
1. Công thức lũy thừa:
Các tính chất quan trọng:
- Nếu a > 1 thì aα > aβ ⇔ α > β
- Nếu 0 < a < 1 thì aα > aβ ⇔ α < β thì α < β
2. Công thức căn bậc n
II. Hàm số mũ
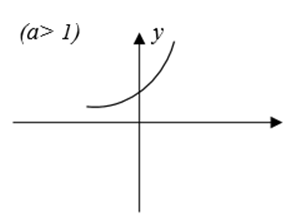
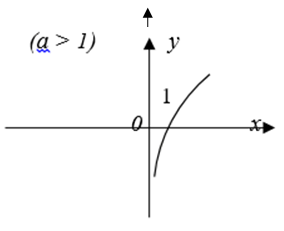
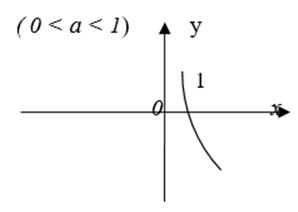
1. Định nghĩa: Cho a > 0, a ≠ 1 ( cố định). Hàm số mũ là hàm số xác định bởi công thức : y = ax ( x ∈ R)
2. Tính chất:
a) Hàm số mũ liên tục trên R
b) y = ax > 0 mọi x ∈ R
c) a > 1 : Hàm số đồng biến
ax1 < ax2 ⇔ x1 < x2
d) 0 < a < 1 : Hàm số nghịch biến
ax1 < ax2 ⇔ x1 > x2
Chú ý : ax1 < ax2 ⇔ x1 = x2
3. Đồ thị :
4. Phương trình và bất phương trình mũ:
a. Phương trình mũ:
+) ax = b ⇔ x = logab
+) afx = b ⇔ f(x) = logab
+) a(fx) = ag(x) ⇔ f(x) = g(x)
b. Bất phương trình mũ:
+) ax > b ⇔ x > logab nếu a > 1
afx > b ⇔ f(x) > logab nếu a > 1
+) ax > b ⇔ x < logab nếu 0 < a < 1
afx > b ⇔ f(x) < logab nếu 0 < a < 1
+) af(x) > ag(x) ⇔ f(x) > g(x) nếu a > 1
af(x) > ag(x) ⇔ f(x) < g(x) nếu 0 < a < 1
III. Hàm số Lôgarit
1. Định nghĩa :
a) Cho a > 0, a ≠ 1 , N > 0
Logarit cơ số a của N là số mũ M sao cho : aM = N
Ký hiệu : logaN = M
b) Hàm số logarit theo cơ số a ( a > 0, a ≠ 1 ) của đối số x là hàm số được cho bởi công thức: y = logax ( với x > 0, a > 0, a ≠ 1)
2. Đồ thị:
3. Công thức lôgarit:
+) loga1 = 0
+) logaa = 1
+) logabα = αlogab Đặc biệt: 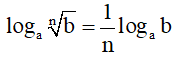
+) 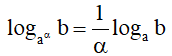
+) logabc = logb + logac (lôgarit của tích bằng tổng các lôgarit)
+) 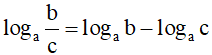
+)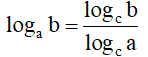
+)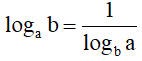
+)logab.logbc = logac
+)a logbc = clogba Đặc biệt: a loaab = b
Các tính chất quan trọng:
- Nếu a > 1 thì loga α > loga β ⇔ α > β
- Nếu 0 < a < 1 thì loga α > loga β ⇔ α < β
4. Phương trình và bất phương trình lôgarit:
a. Phương trình lôgarit:
+) logax = b ⇔ x = ab
+) logaf(x) = b ⇔ f(x) = ab
+) logaf(x) = logag(x) ⇔ f(x) = g(x)
b.Bất phương trình lôgarit:
+) logax > b ⇔ x > ab nếu a > 1
logaf(x) > b ⇔ f(x) > ab nếu a > 1
+) logax > b ⇔ x < ab nếu 0 < a < 1
logaf(x) > b ⇔ f(x) < ab nếu 0 < a < 1
+) logaf(x) > loga g(x) ⇔ f(x) > g(x) nếu a > 1
+) logaf(x) > loga g(x) ⇔ f(x) < g(x) nếu 0 < a < 1
Lưu ý đặt điều kiện cho phương trình, bất phương trình mũ và lôgarit:
+) af(x) → Không có điều kiện.
+) logf(x)g(x) Điều kiện:
+) Đặt t = ax → Điều kiện: t > 0
+) Đặt t = logax → Không có điều kiện t
Công thức giải nhanh Toán lớp 12 Chương 3 Giải tích chi tiết nhất
1. Công thức nguyên hàm:
2. Phương pháp đổi biến số dạng 1:
Một số cách đổi biến thường gặp:
+) Nếu biểu thức dưới dấu tích phân có chứa 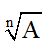
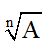
+) Khi tính tích phân dạng 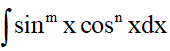
- Nếu m và n chẵn ta dùng công thức hạ bậc.
- Nếu m chẵn, n lẻ ta đặt t = sinx .
- Nếu m lẻ, n chẵn ta đặt t = cosx .
3. Phương pháp đổi biến số dạng 2:
- Hàm có chứa 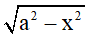
- Hàm có chứa 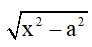
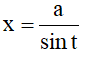
- Hàm có chứa 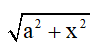
4. Tích phân từng phần: 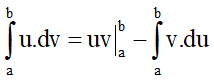
Thứ thự ưu tiên: Inx → P(x) → 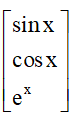
5. Phương pháp tính tích phân của hàm hữu tỉ:
- Bậc của P(x) ≥ Bậc của Q(x) : Chia đa thức tử cho mẫu.
- Bậc của P(x) < Bậc của Q(x) : → Phân tích mẫu thành tích và biến đổi theo cách sau:
Đặc biệt :
6. Tính diện tích hình phẳng
- Loại 1: Hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành, hai đường thẳng x = a , x = b .
Công thức: 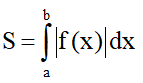
- Loại 2: Hình phẳng (H) giới hạn bởi hai đồ thị đồ thị hàm số y = F(x) , y = g(x) hai đường thẳng x = a , x = b .
Công thức: 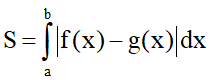
7. Tính thể tích vật thể tròn xoay: Cho hình (H) giới hạn bởi đồ thị hàm số y = f(x) , trục hoành và hai đường thẳng x = a , x = b quay quanh trục hoành tạo thành vật thể tròn xoay có thể tích là:
Công thức giải nhanh Toán lớp 12 Chương 4 Giải tích chi tiết nhất
1. Định nghĩa số phức: Số phức là 1 biểu thức có dạng z = a + bi , trong đó a,b là các số thực, i2 = -1 .
a: được gọi là phần thực
b: được gọi là phần ảo
- Tập hợp các số phức được ký hiệu là 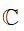
- Số phức có phần thực bằng 0 được gọi là số thuần ảo.
- Hai số phức bằng nhau: khi và chỉ khi có phần thực bằng nhau và phần ảo bằng nhau. 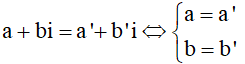
- Môđun của số phức : 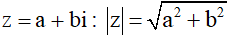
- Số phức liên hợp: của số phức 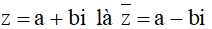
- Phép cộng hai số phức:
(a + bi) + (a' + b'i) = (a + a') + (b + b')i
- Phép trừ hai số phức: (a + bi) - (a' + b'i) = (a - a') + (b - b')i
- Phép nhân hai số phức:
(a + bi).(a' + b'i) = (aa' - bb') + (ab' + ba')i
- Phép chia hai số phức:

- Số phức nghịch đảo của z là: 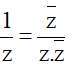
2. Giải phương trình bậc hai với hệ số thực trên tập số phức:
Cho phương trình bậc hai
Δ = b2 - 4ac
+) Δ < 0 : Phương trình có 2 nghiệm phức phân biệt:
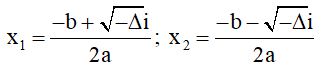
+) Δ = 0 : Phương trình có nghiệm kép thực : 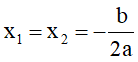
+) Δ > 0 : Phương trình có 2 nghiệm thực phân biệt:
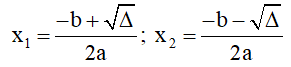
Chú ý:
+) Khi giải phương trình trùng phương az4 + bz2 + c trên tập số phức 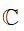
+) 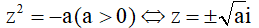
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

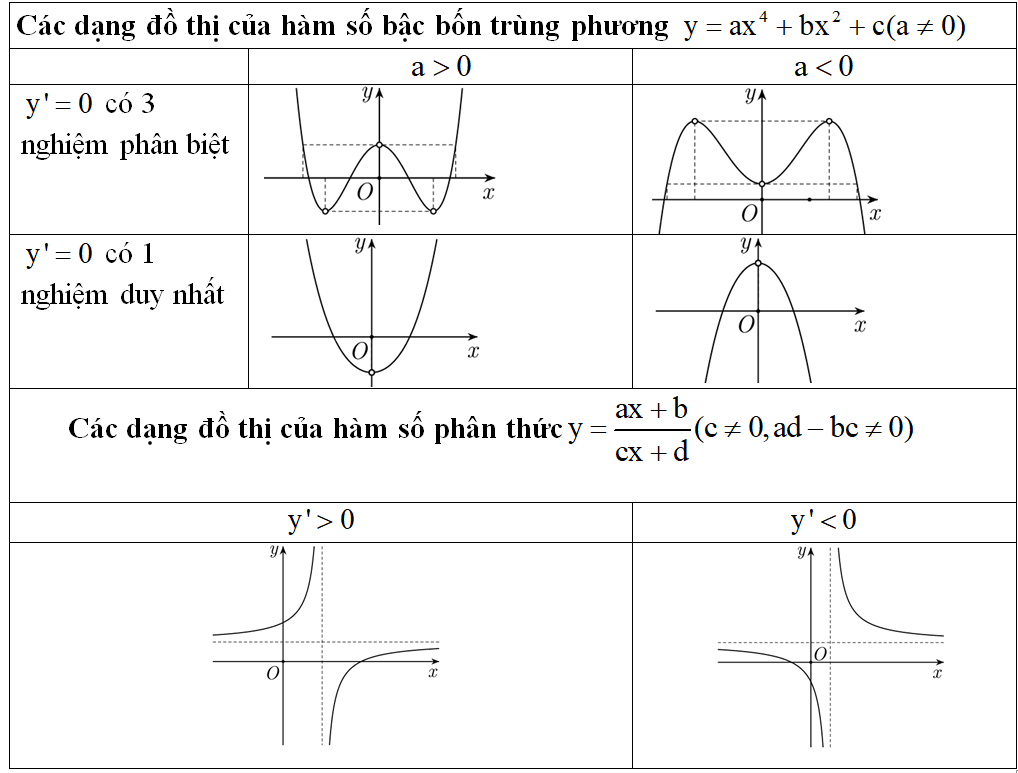
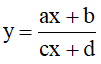
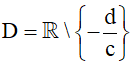
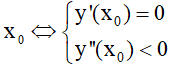
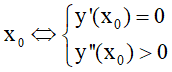
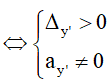
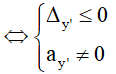
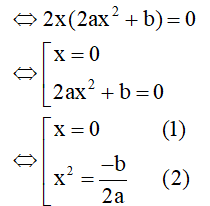
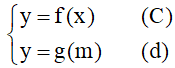

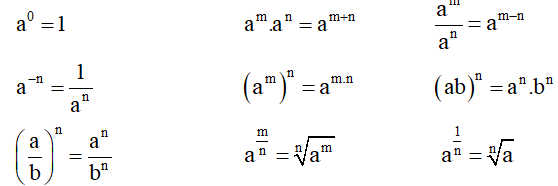

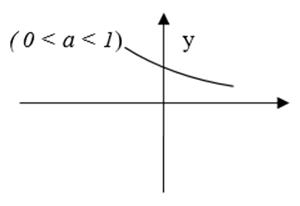
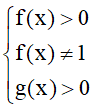
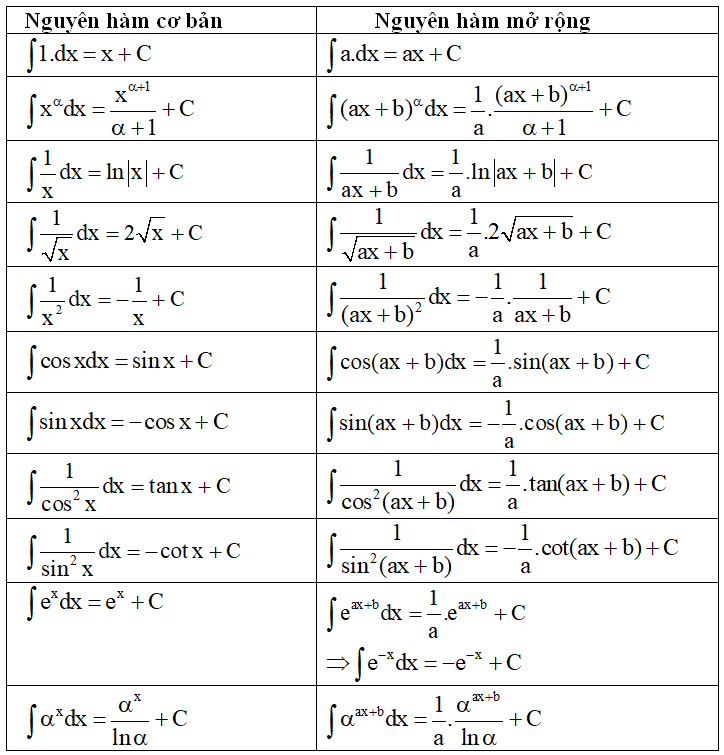
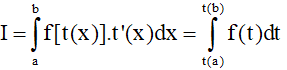
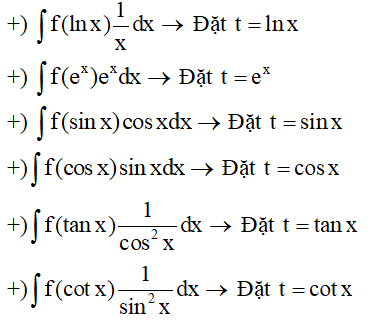
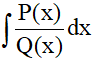
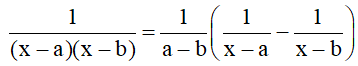
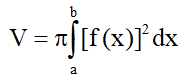
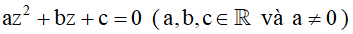






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

