Công thức xác định GTNN - GTLN của hàm số (siêu hay)
Công thức xác định GTNN - GTLN của hàm số Toán 12 sẽ giúp học sinh lớp 12 nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.
Công thức xác định GTNN - GTLN của hàm số (siêu hay)
1. Công thức
* Định nghĩa
Cho hàm số y = f(x) xác định trên tập D.
+ Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) ≤ M ∀ x ∈ D và tồn tại x0 ∈ D: f(x0) = M.
Kí hiệu là: .
+ Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) ≥ M ∀ x ∈ D và tồn tại x1 ∈ D: f(x1) = m.
Kí hiệu là: .
* Các bước tìm GTLN - GTNN của hàm số trên D hoặc trên một khoảng xác định
Bước 1. Tìm tập xác định của hàm số y = f(x).
Bước 2. Tính đạo hàm y'. Tìm những điểm mà đạo hàm bằng 0 hoặc không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Dựa vào bảng biến thiên và kết luận GTLN; GTNN của hàm số.
- Lưu ý: GTLN, GTNN của hàm số phải là số hữu hạn.
Trong một vài TH (thường là hàm phân thức) GTLN, GTNN hữu hạn nhưng đạt tại x = ±∞. Khi đó ta cũng kết luận là hàm số không có GTLN (GTNN).
* Cách tính GTLN và GTNN trên một đoạn
a. Định lí: Mọi hàm số liên tục trên một đoạn đều có GTLN và GTNN trên đoạn đó.
b. Các bước tìm GTLN, GTNN của hàm số y = f(x) trên đoạn [a; b]
Bước 1. Tìm các điểm x1, x2, …, xn thuộc khoảng (a; b) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 2. Tính f(x1), f(x2), …, f(xn), f(a) và f(b).
Bước 3. So sánh các số tìm được ở Bước 2.
- Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.
- Kết luận: và .
- Chú ý: Đối với hàm phân thức y = . Khi tìm GTLN và GTNN của hàm này trên đoạn [m;n].
+) Nếu thì hàm số không có GTLN và GTNN.
+) Nếu thì GTLN và GTNN sẽ đạt tại các đầu mút.
2. Ví dụ minh họa
Ví dụ 1. Tìm GTLN và GTNN của các hàm số sau:
a) trên khoảng (0; +∞);
b) trên khoảng (–∞; +∞).
Lời giải
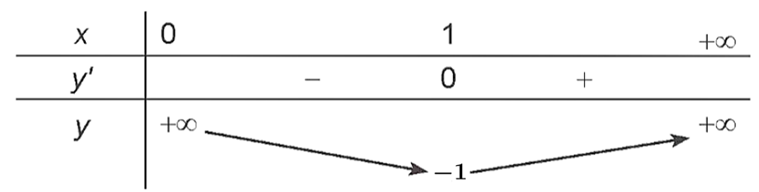
a) Trên khoảng (0; +∞), ta có: ; y' = 0 khi x = 1.
Bảng biến thiên của hàm số trên khoảng (0; +∞) như sau:
Từ bảng biến thiên ta thấy và không tồn tại giá trị lớn nhất của hàm số.
b) Ta có: ;
y’ = 0 khi x = –2 hoặc x = 2.
Bảng biến thiên của hàm số như sau:
Dựa vào bảng biến thiên, ta thấy và .
Ví dụ 2. Tìm GTLN, GTNN của các hàm số sau:
a) y = x3 + 3x2 – 9x – 7 trên đoạn [– 4; 3];
b) y = x4 – 4x2 + 3 trên đoạn [1; 3].
Lời giải
a) Ta có y' = 3x2 + 6x – 9.
Trên khoảng (– 4; 3), y' = 0 khi x = – 3 hoặc x = 1.
Tính: y(– 4) = 13; y(– 3) = 20; y(1) = – 12; y(3) = 20.
Suy ra tại x = –3 và x = 3 và tại x = 1.
b) Ta có y' = 4x3 – 8x.
Trên khoảng (1; 3), y' = 0 khi x = .
Tính: y(1) = 0; y() = – 1; y(3) = 48.
Vậy tại x = và tại x = 3.
3. Bài tập tự luyện
Bài 1. Tìm GTLN và GTNN của hàm số:
a) y = 2x3 – 3x2 – 12x + 8 trên đoạn [– 3; 3];
b) y = x4 – 2x2 + 3 trên đoạn [– 2; 0];
c) trên đoạn [– 4; – 1].
Bài 2. Tìm GTLN, GTNN của các hàm số sau:
a) trên đoạn ;
b) y = x3 – 3x2 – 9x + 35 trên các đoạn [– 4; 4] và [– 5; 3];
c) y = 3x + 3– x trên đoạn [– 1; 2];
d) y = ln(x2 + 2x + 3) trên đoạn [2; 4].
Bài 3. Tìm GTLN, GTNN các hàm số sau:
a) ;
b) .
Bài 4. Tìm hai số có hiệu là 13 sao cho tích của chúng bé nhất.
Bài 5. Một chất điểm chuyển động theo phương trình x = 6t2 – t3. Tính thời điểm t (giây) mà tại đó chất điểm có vận tốc lớn nhất.
Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

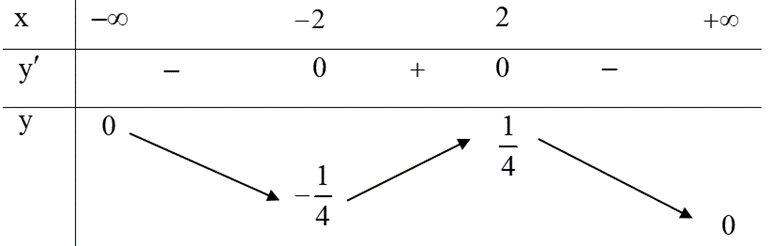



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

