Công thức tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm (siêu hay)

Công thức tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm Toán 12 sẽ giúp học sinh lớp 12 nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.

Công thức tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm (siêu hay)

1. Công thức

a) Khoảng biến thiên của mẫu số liệu ghép nhóm

Cho mẫu số liệu ghép nhóm dưới đây, trong đó n₁ > 0 và n_m > 0.

Gọi a₁, a_{m + 1} lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm m.

Khi đó khoảng biến thiên của mẫu số liệu ghép nhóm được tính như sau:

R = a_{m + 1} – a₁.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm

Xét mẫu số liệu ghép nhóm cho bởi bảng dưới đây:

Ta có: Q₁ = s + $\left(\frac{\frac{n}{4}-c{f}_{p-1}}{n_p}\right).h$, trong đó p là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4}$; s, h, n_p lần lượt là đầu mút trái, độ dài, tần số của nhóm p; cf_{p – 1} là tần số tích lũy của nhóm p – 1.

          Q₃ = t + $\left(\frac{\frac{3n}{4}-c{f}_{q-1}}{n_q}\right).l$, trong đó q là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3n}{4}$; t, l, n_q lần lượt là đầu mút trái, độ dài, tần số của nhóm q; cf_{q – 1} là tần số tích lũy của nhóm q – 1.

Khi đó khoảng tứ phân vị của mẫu số liệu ghép nhóm được tính như sau:

∆Q = Q₃ – Q_1.

2. Ví dụ minh họa

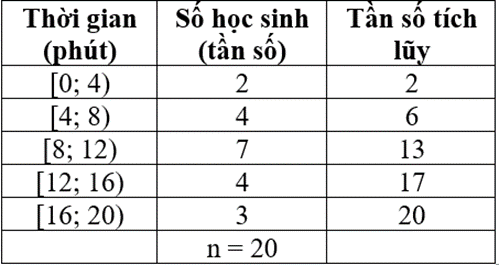
Ví dụ 1. Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của 20 học sinh thu được kết quả sau:

Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a₁ = 0, đầu mút phải của nhóm 5 là a₆ = 20.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

R = a₆ – a₁ = 20 – 0 = 20 (phút).

Ta có bảng dưới đây:

Ta có: $\frac{n}{4}=\frac{20}{4}=5$, nhận thấy 2 < 5 < 6 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 5.

Xét nhóm 2 là nhóm [4; 8) có s = 4; h = 4; n₂ = 4 và nhóm 1 là nhóm [0; 4) có tần số tích lũy là cf₁ = 2.

Do đó Q₁ = 4 + $\left(\frac{5-2}{4}\right).4$ = 7.

Ta có: $\frac{3n}{4}=\frac{3.20}{4}=15$, nhận thấy 13 < 15 < 17 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15.

Xét nhóm 4 là nhóm [12; 16) có t = 12; l = 4; n₄ = 4 và nhóm 3 là nhóm [8; 12) có tần số tích lũy cf₃ = 13.

Do đó, Q₃ = 12 + $\left(\frac{15-13}{4}\right).4$ = 14.

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:

∆Q = Q₃ – Q₁ = 14 – 7 = 7.

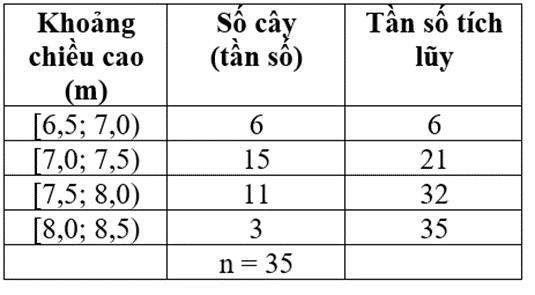
Ví dụ 2. Cho mẫu số liệu ghép nhóm thống kê về chiều cao (mét) của 35 cây bạch đàn trong rừng, ta có bảng số liệu sau:

Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a₁ = 6,5; đầu mút phải của nhóm 4 là a₅ = 8,5.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

R = a₅ – a₁ = 8,5 – 6,5 = 2 (m).

Ta có bảng dưới đây:

Ta có: $\frac{n}{4}=\frac{35}{4}=\mathrm{8,75}$, nhận thấy 6 < 8,75 < 21 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 8,75.

Xét nhóm 2 là nhóm [7,0; 7,5) có s = 7; h = 0,5; n₂ = 15 và nhóm 1 là nhóm [6,5; 7,0) có tần số tích lũy là cf₁ = 6.

Do đó Q₁ = s + $\left(\frac{\frac{n}{4}-c{f}_{p-1}}{n_p}\right).h$ = 7 + $\left(\frac{\mathrm{8,75}-6}{15}\right)\mathrm{.0,5}$ = $\frac{851}{120}$.

Ta có: $\frac{3n}{4}=\frac{3.35}{4}=\mathrm{26,25}$, nhận thấy 21 < 26,25 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 26,25.

Xét nhóm 3 là nhóm [7,5; 8,0) có t = 7,5; l = 0,5; n₃ = 11 và nhóm 2 là nhóm [7,0; 7,5) có tần số tích lũy cf₂ = 21.

Do đó, Q₃ = t + $\left(\frac{\frac{3n}{4}-c{f}_{q-1}}{n_q}\right).l$ = 7,5 + $\left(\frac{\mathrm{26,25}-21}{11}\right)\mathrm{.0,5}$ = $\frac{681}{88}$.

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:

∆Q = Q₃ – Q₁ = $\frac{681}{88}-\frac{851}{120}$ = $\frac{427}{660}$ ≈ 0,647.

3. Bài tập tự luyện

Bài 1. Trong mỗi phương án a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).

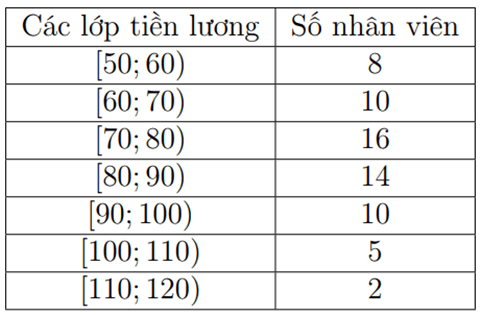
Tiền lương nhận được trong 1 giờ làm việc của nhân viên trong công ty A được thống kê theo mẫu số liệu ghép nhóm sau (đơn vị: nghìn đồng).

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 10.	Đ	S
b) Tứ phân vị thứ nhất Q1 = 69.	Đ	S
c) Tứ phân vị thứ ba Q3 = 90,75.	Đ	S
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 21,75.	Đ	S

Bài 2. Mức lương hàng tháng ở một công ty được Công đoàn thu thập theo bảng sau (đơn vị: triệu đồng):

Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu trên.

Bài 3. Một vận động viên được ghi lại cự li 30 lần ném lao của mình ở bảng sau (đơn vị: mét):

a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên với 5 nhóm tương ứng:

[69,2; 70); [70; 70,8); [70,8; 71,6); [71,6; 72,4); [72,4; 73,2).

b) Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu trên.

Bài 4. Khảo sát thời gian xem ti vi trong một ngày của một số học sinh lớp 11 thu được mẫu số liệu ghép nhóm sau:

Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Bài 5. Số cuộc gọi điện thoại của một người thực hiện mỗi ngày trong vòng 1 tháng được thống kê trong bảng sau:

Hãy tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu trên.

Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:

• Công thức tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

• Các công thức về tính chất của nguyên hàm

• Công thức nguyên hàm của một số hàm số sơ cấp

• Các công thức về tính chất của tích phân

• Công thức tích phân của một số hàm số sơ cấp

---