Đề thi Học kì 2 Toán lớp 7 có đáp án (6 đề)

Siêu sale sách Toán - Văn - Anh Vietjack 25-11 trên Shopee mall

Đề thi Học kì 2 Toán lớp 7 có đáp án (6 đề)

Đề thi Học kì 2 Toán lớp 7 có đáp án gồm 6 đề thi chọn lọc giúp học sinh ôn tập và đạt kết quả cao trong bài thi Học kì 2 Toán 7.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

Bài 1: (2,0 điểm) Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây:

8	5	7	8	9	7	8	9	12	8
6	7	7	7	9	8	7	6	12	8
8	7	7	9	9	7	9	6	5	12

a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?

b) Lập bảng “tần số”.

c) Tính số trung bình cộng (làm tròn một chữ số thập phân) và mốt của dấu hiệu.

Bài 2: (2,0 điểm) Cho đơn thức A = $(- \frac{2}{5} x^{3} y^{4}) . (\frac{5}{6} x y^{2} z) .$

a) Thu gọn đơn thức A.

b) Xác định hệ số và bậc của đơn thức.

Bài 3: (2,0 điểm) Cho hai đa thức f(x) = 5 + 3x² - x - 2x² và g(x) = 3x + 3 - x - x².

a) Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.

b) Tính h(x) = f(x) + g(x).

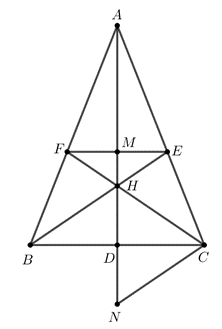
Bài 4: (3,5 điểm) Cho tam giác ABC cân (AB = AC). Các đường phân giác BE, CF cắt nhau tại H.

a) Chứng minh $Δ A B E = Δ A C F .$

b) Tia AH cắt BC tại D. Chứng minh D là trung điểm của BC và EF // BC.

c) Chứng minh AH là trung trực của EF. So sánh HF và HC.

d) Tìm điều kiện của tam giác ABC để HC = 2.HD.

Bài 5: (0,5 điểm) Cho đa thức f(x) thỏa mãn f(x) + x.f(-x) = x + 1 với mọi giá trị của x. Tính f(1).

Đáp án

Bài 1: (2,0 điểm)

a) - Dấu hiệu ở đây là thời gian giải một bài toán (tính theo phút) của 30 học sinh.

- Số các giá trị là 30.

b) Ta có bảng tần số:

Giá trị (x)	5	6	7	8	9	12
Tần số (n)	2	3	9	7	6	3	N = 30

c) Trung bình cộng của dấu hiệu bằng:

$\frac{5.2 + 6.3 + 7.9 + 8.7 + 9.6 + 12.3}{2 + 3 + 9 + 7 + 6 + 3} = \frac{237}{30} = \frac{79}{10} = 7, 9$

Mốt của dấu hiệu bằng 7.

Bài 2: (2,0 điểm)

a) A = $(- \frac{2}{5} x^{3} y^{4}) . (\frac{5}{6} x y^{2} z)$

A = $(- \frac{2}{5} . \frac{5}{6})$ . (x³ . x) . (y⁴ . y² ) . z

A = $\frac{- 1}{3}$ x⁴y⁶z.

Vậy A = $\frac{- 1}{3}$ x⁴y⁶z.

b) Hệ số của đơn thức A là: $\frac{- 1}{3}$

Bậc của đơn thức A là: 4 + 6 + 1 = 11.

Bài 3: (2,0 điểm)

a) f(x) = 5 + 3x² - x - 2x²

f(x) = (3x² - 2x²) - x + 5

f(x) = x² - x + 5

g(x) = - x²+ (3x - x) + 3

g(x) = - x²+ 2x + 3

b) h(x) = f(x) + g(x)

h(x) = x² - x + 5 + (-x²) + 2x + 3

h(x) = (x² - x²) + (-x + 2x) + (5 + 3)

h(x) = x + 8

Vậy h(x) = x + 8.

Bài 4: (3,5 điểm)

a) Do $Δ A B C$ cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B} .$

Do BE là tia phân giác của $\hat{A B C}$ nên $\hat{A B E} = \frac{1}{2} \hat{A B C} .$

Do CF là tia phân giác của $\hat{A C B}$ nên $\hat{A C F} = \frac{1}{2} \hat{A C B} .$

Do đó $\hat{A B E} = \hat{A C F} .$

Xét $Δ A B E$ và $Δ A C F$ có:

$\hat{A}$ chung

AB = AC (chứng minh trên)

$\hat{A B E} = \hat{A C F}$ (chứng minh trên)

$\Rightarrow Δ A B E = Δ A C F (g - c - g) .$

b) Do hai đường phân giác BE và CF của $Δ A B C$ cắt nhau tại H nên AH là đường phân giác của $\hat{B A C}$ hay AD là đường phân giác của $\hat{B A C}$

$Δ A B C$ cân tại A có AD là đường phân giác của nên AD vừa là đường phân giác, vừa là đường trung trực của $Δ A B C$ .

Do đó D là trung điểm của BC.

Do $Δ A B E = Δ A C F$ nên AE = AF (2 cạnh tương ứng).

$Δ A E F$ có AE = AF nên $Δ A E F$ cân tại A.

Do đó $\hat{A E F} = \hat{A F E}$ .

Xét trong $Δ A B C$ : $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$

Mà $\hat{A B C} = \hat{A C B}$ nên $2 \hat{A C B} + \hat{B A C} = 180 °$

$\Rightarrow \hat{A C B} = \frac{180 ° - \hat{B A C}}{2}$ (1).

Xét trong $Δ A E F$ : $\hat{A F E} + \hat{A E F} + \hat{E A F} = 180 °$

Mà $\hat{A E F} = \hat{A F E}$ nên $2 \hat{A E F} + \hat{E A F} = 180 °$

$\Rightarrow \hat{AEF} = \frac{180 ° - \hat{E A F}}{2}$ (2).

Từ (1) và (2) suy ra $\hat{A C B} = \hat{A EF} .$

Mà hai góc này ở vị trí đồng vị nên EF // BC.

c) Gọi M là giao điểm của AH và EF.

Do AH là đường phân giác của $\hat{B A C}$ nên AM là đường phân giác của $\hat{EAF}$ .

$Δ A E F$ cân tại A, có AM là đường phân giác nên AM vừa là đường phân giác, vừa là đường trung trực của $Δ A E F$ .

Do đó AM là đường trung trực của EF hay AH là đường trung trực của EF.

Do BE là đường phân giác của $\hat{A B C}$ nên $\hat{H B C} = \frac{1}{2} \hat{A B C}$ .

Do CF là đường phân giác của $\hat{A C B}$ nên $\hat{H C B} = \frac{1}{2} \hat{A C B} .$

Mà $\hat{A B C} = \hat{A C B}$ nên $\hat{H B C} = \hat{H C B}$ .

$Δ H B C$ có $\hat{H B C} = \hat{H C B}$ nên $Δ H B C$ cân tại H.

Do đó HB = HC.

Ta có $\hat{B F H}$ là góc ngoài tại đỉnh F của $Δ A F C$ nên $\hat{B F H} = \hat{F A C} + \hat{F C A}$ .

Do đó $\hat{B F H} > \hat{F C A}$ .

Do $\hat{A B E} = \hat{A C F}$ nên $\hat{F C A} = \hat{F B H}$ .

Do đó $\hat{B F H} > \hat{F B H}$ .

Xét $Δ B F H$ có $\hat{B F H} > \hat{F B H}$ nên HB > HF hay HC > HF.

d) Trên tia đối của DH lấy điểm N sao cho DN = DH.

Khi đó HN = HC = 2HD.

Do AD là đường trung trực của BC nên $A D ⊥ BC.$

$Δ H C N$ có D là trung điểm của HN mà $C D ⊥ H N$ nên $Δ H C N$ cân tại C.

Khi đó HC = CN.

Do đó HN = HC = CN.

$Δ H C N$ có HN = HC = CN nên đều.

Khi đó $\hat{N H C}$ = 60^o.

Xét vuông tại D: $\hat{D H C} + \hat{H C D} = 90 °$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Do đó $\hat{H C D} = 90 ° - \hat{D H C} = 90 ° - 60 ° = 30 ° .$

Mà $\hat{H C D} = \frac{1}{2} \hat{A C B}$ nên $\hat{A C B} = 60 ° .$

$Δ A B C$ cân tại A có $\hat{A C B} = 60 °$ nên $Δ A B C$ là tam giác đều.

Vậy $Δ A B C$ là tam giác đều thì HC = 2HD.

Bài 5: (0,5 điểm)

Thay x = 1 vào f(x) + x.f(-x) = x + 1 ta được:

f(1) + f(-1) = 1 + 1

f(1) + f(-1) = 2

Thay x = -1 vào f(x) + x.f(-x) = x + 1 ta được:

f(-1) + (-1).f(1) = -1 + 1

f(-1) - f(1) = 0.

Do đó f(-1) = f(1).

Mà f(1) + f(-1) = 2 nên 2f(1) = 2 do đó f(1) = 1.

Vậy f(1) = 1.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 2)

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Biểu thức nào sau đây không là đơn thức?

A. 4x²y(-2x).

B. 2x.

C. 2xy - x².

D. 2021.

Câu 2. Bậc của đơn thức -2x³y⁵ là:

A. -2.

B. 3.

C. 8.

D. x³y⁵.

Câu 3. Bậc của đa thức A = x²y⁴- x³y⁵ - x⁷ + 9 là:

A. 6.

B. 7.

C. 8.

D. 9.

Câu 4. Cho tam giác ABC cân tại A có Số đo góc B là:

A. 50^o.

B. 60^o.

C. 70^o.

D. 80^o.

Câu 5. Giao điểm 3 đường cao của một tam giác gọi là:

A. trọng tâm của tam giác.

B. trực tâm của tam giác.

C. tâm đường tròn ngoại tiếp tam giác.

D. điểm cách đều 3 cạnh của tam giác.

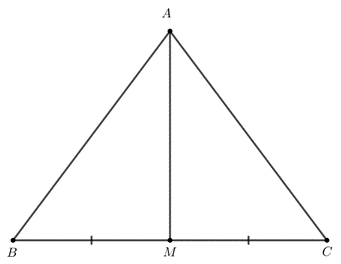
Câu 6. Cho tam giác ABC cân tại A có AB = 5 cm, BC = 6 cm và AM là đường trung tuyến. Độ dài đoạn AM là:

A. 3 cm.

B. $\sqrt{61}$ cm.

C. $\sqrt{11}$ cm.

D. 4 cm.

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm)

a) Tính giá trị biểu thức: 4x³ - 3xy tại x = $\frac{- 1}{2}$ ; y = 6.

b) Cho đơn thức A = (-3xy) . $(\frac{2}{3} x^{2} y)$ . Hãy thu gọn đơn thức và chỉ ra hệ số, phần biến của đơn thức A.

Bài 2. (2,0 điểm) Tìm tất cả nghiệm của mỗi đa thức sau:

a) A = 2(-x + 5) - $\frac{3}{2}$ (x - 4).

b) B = -4x² + 9.

c) C = x³ + 4x.

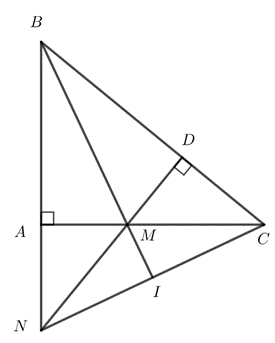
Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Trên cạnh BC lấy điểm D sao cho BD = 3 cm. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.

a) Tính AC và so sánh các góc của tam giác ABC.

b) Chứng minh MA = MD và tam giác MNC cân.

c) Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.

Bài 4. (0,5 điểm) Tính giá trị của biểu thức $\frac{4 a - b}{3 a + 3} + \frac{4 b - a}{3 b - 3}$ với a - b = 3; a ≠ -1; b ≠ 1.

Đáp án

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Biểu thức nào sau đây không là đơn thức?

A. 4x²y(-2x).

B. 2x.

C. 2xy - x².

D. 2021.

Hướng dẫn giải

Đáp án đúng là: C

2xy - x² là đa thức nên chọn đáp án C.

Câu 2. Bậc của đơn thức -2x³y⁵ là:

A. -2.

B. 3.

C. 8.

D. x³y⁵.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đơn thức -2x³y⁵ là 3 + 5 = 8 nên chọn đáp án C.

Câu 3. Bậc của đa thức A = x²y⁴- x³y⁵ - x⁷ + 9 là:

A. 6.

B. 7.

C. 8.

D. 9.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đa thức A = x²y⁴- x³y⁵ - x⁷ + 9 là bậc của hạng tử - x³y⁵.

Bậc của hạng tử - x³y⁵ là: 3 + 5 = 8 nên chọn đáp án C.

Câu 4. Cho tam giác ABC cân tại A có $\hat{A} = 40 ° .$ Số đo góc B là:

A. 50^o.

B. 60^o.

C. 70^o.

D. 80^o.

Hướng dẫn giải

Đáp án đúng là: C

Cho tam giác ABC cân tại A nên $\hat{B} = \hat{C}$ , mà $\hat{A} + \hat{B} + \hat{C} = 180 °$ nên $\hat{A} + 2 \hat{B} = 180 °$

Do đó $\hat{B} = \frac{180 ° - \hat{A}}{2} = \frac{180 ° - 40 °}{2}$ = 70^o.

Chọn đáp án C.

Câu 5. Giao điểm 3 đường cao của một tam giác gọi là:

A. trọng tâm của tam giác.

B. trực tâm của tam giác.

C. tâm đường tròn ngoại tiếp tam giác.

D. điểm cách đều 3 cạnh của tam giác.

Hướng dẫn giải

Đáp án đúng là: B

Giao điểm 3 đường cao của một tam giác gọi là trực tâm của tam giác (theo định nghĩa) nên chọn đáp án B.

Câu 6. Cho tam giác ABC cân tại A có AB = 5 cm, BC = 6 cm và AM là đường trung tuyến. Độ dài đoạn AM là:

A. 3 cm.

B. $\sqrt{61}$ cm.

C. $\sqrt{11}$ cm.

D. 4 cm.

Hướng dẫn giải

Đáp án đúng là: D

$Δ A B C$ cân tại A có AM là đường trung tuyến nên AM vừa là đường trung tuyến, vừa là đường cao của $Δ A B C$ .

Do AM là đường trung tuyến nên M là trung điểm của BC.

Do đó BM = $\frac{1}{2}$ BC = $\frac{1}{2}$ .6 = 3 cm.

Áp dụng định lý Pytago vào vuông tại M có:

AM² + BM² = AB²

$\Rightarrow$ AM² = AB²- BM²

$\Rightarrow$ AM² = 5²- 3²

$\Rightarrow$ AM² = 25 - 9

$\Rightarrow$ AM² = 16

$\Rightarrow$ AM = 4 cm

Chọn đáp án D.

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm)

a) Với x = $\frac{- 1}{2}$ ; y = 6 thì 4x³ ${(\frac{- 1}{2})}^{3}$ - 3xy = 4. - 3. $(\frac{- 1}{2})$ .6

= 4. $\frac{{(- 1)}^{3}}{2^{3}}$ - 3.(-3) = 4. $(\frac{- 1}{8})$ + 9 = (-2) + 9 = 7.

Vậy 4x³ - 3xy = 7 tại x = $\frac{- 1}{2}$ ; y = 6.

b) A = (-3xy) . $(\frac{2}{3} x^{2} y)$

A = $(- 3. \frac{2}{3})$ .(x.x²).(y.y)

A = -2x³y².

Hệ số của đơn thức A: -2.

Phần biến của đơn thức A: x³y².

Bài 2. (2,0 điểm)

a) A = 2(-x + 5) - $\frac{3}{2}$ (x - 4)

A = 2.(-x) + 2.5 - $\frac{3}{2}$ x + $\frac{3}{2} .4$

A = (-2x) + 10 - $\frac{3}{2} x$ + 6

A = (-2 - $\frac{3}{2}$ )x + 16

A = $(- \frac{4}{2} - \frac{3}{2})$ x + 16

A = $\frac{- 7}{2}$ x + 16

Để A = 0 thì $\frac{- 7}{2}$ x + 16 = 0

$\Rightarrow$ x = - 16

$\Rightarrow$ x = $- 16 : (\frac{- 7}{2})$

$\Rightarrow$ x = $- 16. (\frac{2}{- 7})$

$\Rightarrow$ x = $\frac{32}{7}$

Vậy x = $\frac{32}{7}$ .

b) B = -4x² + 9

Để B = 0 thì -4x² + 9 = 0

$\Rightarrow$ -4x² = -9

$\Rightarrow$ x² = $\frac{9}{4}$

Trường hợp 1. x² = ${(\frac{3}{2})}^{2}$

$\Rightarrow x = \frac{3}{2}$

Trường hợp 2. x² = ${(- \frac{3}{2})}^{2}$

$\Rightarrow x = - \frac{3}{2}$

Vậy x = $\frac{3}{2}$ hoặc x = $- \frac{3}{2}$ .

c) C = x³ + 4x

C = x(x² + 4)

Do x² ≥ 0 với mọi x nên x² + 4 > 0 với mọi x.

Do đó C = 0 khi x = 0.

Vậy x = 0.

Bài 3. (3,0 điểm)

a) Áp dụng định lý Pytago vào tam giác ABC vuông tại A:

AB² + AC² = BC²

$\Rightarrow$ 3² + AC² = 5²

$\Rightarrow$ AC² = 25 - 9

$\Rightarrow$ AC² = 16

$\Rightarrow$ AC = 4 cm.

$Δ A B C$ vuông tại A nên $\hat{B A C}$ là góc lớn nhất trong $Δ A B C$

AB < AC nên $\hat{A C B} < \hat{A B C}$ .

Vậy $\hat{A C B} < \hat{A B C} < \hat{B A C} .$

b) Xét $Δ A B M$ vuông tại A và $Δ D B M$ vuông tại D có:

AB = BD (theo giả thiết)

BM chung.

$\Rightarrow Δ A B M = Δ D B M$ (cạnh huyền - cạnh góc vuông).

$\Rightarrow$ MA = MD (2 cạnh tương ứng).

Xét $Δ A M N$ vuông tại A và $Δ D M C$ cân tại D có:

AM = DM (chứng minh trên).

$\hat{A M N} = \hat{D M C}$ (2 góc đối đỉnh).

$\Rightarrow Δ A M N = Δ D M C$ (góc nhọn - cạnh góc vuông).

$\Rightarrow$ MN = MC (2 cạnh tương ứng).

$Δ M N C$ có MN = MC nên $Δ M N C$ cân tại M.

c) Xét $Δ B C N$ có $C A ⊥ B N;$ $N D ⊥ B C$ .

Mà CA cắt ND tại M nên M là trực tâm của $Δ B C N$ .

Do đó $B M ⊥ N C$ (1).

$Δ M N C$ cân tại M, lại có I là trung điểm của NC nên $M I ⊥ N C$ (2).

Từ (1) và (2) suy ra B, M, I thẳng hàng.

Vậy B, M, I thẳng hàng.

Bài 4. (0,5 điểm)

$\frac{4 a - b}{3 a + 3} + \frac{4 b - a}{3 b - 3} = \frac{3 a + a - b}{3 a + 3} + \frac{4 b - a}{3 b - (a - b)}$

$\frac{4 a - b}{3 a + 3} + \frac{4 b - a}{3 b - 3} = \frac{3 a + a - b}{3 a + 3} + \frac{4 b - a}{3 b - (a - b)}$ = 1 + 1 = 2.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 3)

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Tích của hai đơn thức $- \frac{1}{2}$ x²y² và 6xy³ là:

A. 3x³y⁶.

B. -3x³y⁵.

C. 3x²y⁶.

D. $\frac{- 1}{3}$ x²y⁶.

Câu 2. Hệ số cao nhất của đa thức P(x) = 2x³ + x⁴ - 8x² + 20 là:

A. 1.

B. 2.

C. -8.

D. 20.

Câu 3. Giá trị của đa thức P = x²y + 2xy + 3 tại x = -1, y = 2 là:

A. 8.

B. 1.

C. 5.

D. -1.

Câu 4. Cho tam giác ABC có $\hat{B}$ tù, $\hat{A} > \hat{C} .$ Khẳng định nào sau đây là đúng?

A. AC > BC > AB.

B. BC > AB > AC.

C. AB > AC > BC.

D. AC > AB > BC.

Câu 5. Cho hai đa thức P(x) = -x³ + 2x² + x - 1 và Q(x) = x³ - x² - x + 2. Nghiệm của đa thức P(x) + Q(x) là:

A. Vô nghiệm.

B. -1.

C. 1.

D. 0.

Câu 6. Bậc của đa thức A = x²y⁴ - x²y⁵ - 8x⁶ + 2021¹⁸ là:

A. 6.

B. 18.

C. 7.

D. 2021.

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm) Cho hai đa thức:

f(x) = -6x³ - x⁴ + 3x² + 2x⁴ - x - x² + 1 và g(x) = 2x³ - x + x² + x³.

a) Thu gọn và sắp xếp các hạng tử của 2 đa thức theo lũy thừa giảm dần của biến.

b) Tìm bậc, hệ số cao nhất, hệ số tự do của f(x) và g(x).

c) Tính h(x) = g(x) - f(x) và h(-1).

Bài 2. (1,5 điểm) Tìm nghiệm của các đa thức sau:

a) M = 2x - $\frac{1}{2} .$

b) N = (x + 5)(4x² - 1).

c) P = 9x³ - 25x.

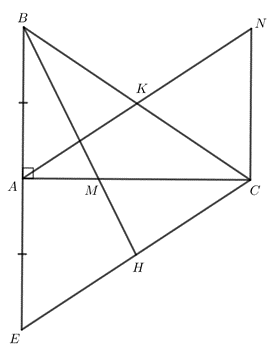
Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A, AB = 9 cm, BC = 15 cm. Trên tia đối của tia AB lấy điểm E sao cho A là trung điểm của BE.

a) Chứng minh rằng $Δ A B C = Δ A E C .$

b) Vẽ đường trung tuyến BH của $Δ B E C$ cắt cạnh AC tại M. Chứng minh M là trọng tâm của $Δ B E C$ và tính độ dài đoạn CM.

c) Từ A vẽ đường thẳng song song với EC, đường thẳng này cắt cạnh BC tại K. Chứng minh rằng ba điểm E, M, K thẳng hàng.

Bài 4. (0,5 điểm) Cho ba số thực x, y, z thỏa mãn x(x² + y) - yz = 0.

Biết rằng trong ba số đó có một số bằng 0, một số âm, một số dương. Hãy chỉ rõ số nào bằng 0, số nào âm, số nào dương.

Đáp án

I. Trắc nghiệm (3,0 điểm) Khoanh tròn trước chữ cái đứng trước câu trả lời đúng

Câu 1. Tích của hai đơn thức $- \frac{1}{2}$ x²y² và 6xy³ là:

A. 3x³y⁶.

B. -3x³y⁵.

C. 3x²y⁶.

D. $\frac{- 1}{3}$ x²y⁶.

Hướng dẫn giải

Đáp án đúng là: B

Ta có $(- \frac{1}{2} x^{2} y^{2})$ .6xy³ = $(- \frac{1}{2} .6)$ .(x².x).(y².y³) = -3x³y⁵.

Chọn đáp án B.

Câu 2. Hệ số cao nhất của đa thức P(x) = 2x³ + x⁴ - 8x² + 20 là:

A. 1.

B. 2.

C. -8.

D. 20.

Hướng dẫn giải

Đáp án đúng là: B

Hệ số cao nhất của đa thức P(x) là hệ số của hạng tử 2x³ bằng 2.

Chọn đáp án B.

Câu 3. Giá trị của đa thức P = x²y + 2xy + 3 tại x = -1, y = 2 là:

A. 8.

B. 1.

C. 5.

D. -1.

Hướng dẫn giải

Đáp án đúng là: B

Thay x = -1, y = 2 vào đa thức P ta có:

P = (-1)².2 + 2.(-1).2 + 3 = 1.2 + (-2).2 + 3 = 2 - 4 + 3 = 1.

Chọn đáp án B.

Câu 4. Cho tam giác ABC có $\hat{B}$ tù, $\hat{A} > \hat{C} .$ Khẳng định nào sau đây là đúng?

A. AC > BC > AB.

B. BC > AB > AC.

C. AB > AC > BC.

D. AC > AB > BC.

Hướng dẫn giải

Đáp án đúng là: A

Do $\hat{B}$ tù nên $\hat{B}$ là góc lớn nhất trong tam giác ABC.

Lại có $\hat{A} > \hat{C}$ nên $\hat{B} > \hat{A} > \hat{C}$ .

Cạnh đối diện với $\hat{B}$ là AC, cạnh đối diện với $\hat{A}$ là BC, cạnh đối diện với $\hat{C}$ là AB.

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn nên $\hat{B} > \hat{A} > \hat{C}$ thì

AC > BC > AB.

Chọn đáp án A.

Câu 5. Cho hai đa thức P(x) = -x³ + 2x² + x - 1 và Q(x) = x³ - x² - x + 2. Nghiệm của đa thức P(x) + Q(x) là:

A. Vô nghiệm.

B. -1.

C. 1.

D. 0.

Hướng dẫn giải

Đáp án đúng là: A

Ta có P(x) + Q(x) = -x³ + 2x² + x - 1 + x³ - x² - x + 2

P(x) + Q(x) = (-x³ + x³) + (2x² - x²) + (x - x) + (-1 + 2)

P(x) + Q(x) = x² + 1.

Ta có x² ≥ 0 với mọi x nên x² + 1 > 0 với mọi x.

Do đó không có giá trị của x thỏa mãn x² + 1 = 0.

Khi đó đa thức P(x) + Q(x) vô nghiệm.

Chọn đáp án A.

Câu 6. Bậc của đa thức A = x²y⁴ - x²y⁵ - 8x⁶ + 2021¹⁸ là:

A. 6.

B. 18.

C. 7.

D. 2021.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đa thức A là bậc của hạng tử - x²y⁵.

Bậc của hạng tử - x²y⁵ là 7 nên chọn đáp án C.

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm)

a) f(x) = -6x³ - x⁴ + 3x² + 2x⁴ - x - x² + 1

f(x) = (-x⁴ + 2x⁴) - 6x³ + (3x² - x²) - x + 1

f(x) = x⁴ - 6x³ + 2x² - x + 1

g(x) = 2x³ - x + x² + x³

g(x) = (2x³ + x³) + x² - x

g(x) = 3x³ + x² - x

b) Bậc của f(x): 4

Hệ số cao nhất của f(x): 1

Hệ số tự do của f(x): 1

Bậc của g(x): 3

Hệ số cao nhất của g(x): 3

Hệ số tự do của g(x): 0

c) h(x) = g(x) - f(x)

h(x) = 3x³ + x² - x - (x⁴ - 6x³ + 2x² - x + 1)

h(x) = 3x³ + x² - x - x⁴ + 6x³ - 2x² + x - 1

h(x) = -x⁴ + (3x³ + 6x³) + (x² - 2x²) + (-x + x) - 1

h(x) = -x⁴ + 9x³ - x² - 1

Khi đó h(-1) = -[(-1)]⁴ + 9.(-1)³ - (-1)² - 1 = -1 + (-9) - 1 - 1 = -12.

Bài 2. (1,5 điểm)

a) M = 2x - $\frac{1}{2} .$

b) N = (x + 5)(4x² - 1).

c) P = 9x³ - 25x.

a) Để M = 0 thì 2x - $\frac{1}{2}$ = 0

$\Rightarrow$ 2x = $\frac{1}{2}$

$\Rightarrow$ x = $\frac{1}{2} : 2$

$\Rightarrow$ x = $\frac{1}{2} . \frac{1}{2}$

$\Rightarrow$ x = $\frac{1}{4}$

Vậy x = $\frac{1}{4}$ .

b) Để N = 0 thì (x + 5)(4x² - 1) = 0

Trường hợp 1.

x + 5 = 0

$\Rightarrow$ x = -5

Trường hợp 2. 4x² - 1 = 0

$\Rightarrow$ 4x² = 1

$\Rightarrow$ x² = $\frac{1}{4}$

+) x² = ${(\frac{1}{2})}^{2}$ $\Rightarrow$ x = $\frac{1}{2}$

+) x² = ${(\frac{- 1}{2})}^{2}$ $\Rightarrow$ x = $\frac{- 1}{2}$

Vậy x = -5 hoặc x = $\frac{- 1}{2}$ hoặc x = $\frac{1}{2} .$

Bài 3. (3,0 điểm)

a) Xét $Δ A B C$ vuông tại A và $Δ A E C$ vuông tại A có:

AB = AE (theo giả thiết)

AC chung

$\Rightarrow Δ A B C = Δ A E C$ (2 cạnh góc vuông)

b) Do A là trung điểm của BE nên CA là đường trung tuyến ứng của

Xét $Δ B E C$ có CA và BH là hai đường trung tuyến cắt nhau tại M.

Do đó M là trọng tâm của $Δ B E C$

Do đó CM = $\frac{2}{3}$ CA.

Áp dụng định lý Pytago vào vuông tại A:

AB² + AC² = BC²

9² + AC² = 15²

AC² = 225 - 81

AC² = 144

AC = 12 cm

Khi đó CM = CA = .12 = 8 cm.

Vậy CM = 8 cm.

c) Trên tia đối của tia KA lấy điểm N sao cho KN = KA.

Do $Δ A B C = Δ A E C$ (2 cạnh góc vuông) nên BC = EC (2 cạnh tương ứng) và $\hat{A C B} = \hat{A C E}$ (2 góc tương ứng).

$\Rightarrow \hat{K C A} = \hat{A C E}$ .

Do AK // EC nên $\hat{K A C} = \hat{A C E}$ (2 góc so le trong)

Do đó $\hat{K C A} = \hat{K A C}$ .

$Δ K A C$ có $\hat{K C A} = \hat{K A C}$ nên $Δ K A C$ cân tại K.

Do đó KA = KC.

Mà KA = KN = $\frac{1}{2}$ AN nên KA = KN = KC = $\frac{1}{2}$ AN.

có KA = KN = KC = $\frac{1}{2}$ AN nên vuông tại C.

Xét $Δ A C N$ vuông tại C và $Δ C A E$ vuông tại A:

$\hat{N A C} = \hat{E C A}$ (chứng minh trên).

AC chung.

$\Rightarrow Δ A C N = Δ C A E$ (góc nhọn - cạnh góc vuông).

$\Rightarrow$ AN = CE (2 cạnh tương ứng).

Mà EC = BC nên AN = BC.

Mà AN = 2AK nên BC = 2AK.

Lại có AK = KC nên BC = 2KC.

Do đó K là trung điểm của BC.

$Δ B E C$ có M là trọng tâm, lại có K là trung điểm của BC nên E, M, K thẳng hàng.

Vậy E, M, K thẳng hàng.

Bài 4. (0,5 điểm)

Nếu x = 0 thì 0.(0² + y) - yz = 0

$\Rightarrow$ -yz = 0.

Khi đó y = 0 hoặc z = 0 (vô lí do chỉ có 1 số bằng 0).

Do đó x ≠ 0.

Nếu y = 0 thì x.(x² + 0) - 0.z = 0

$\Rightarrow$ x³ = 0.

Khi đó x = 0 (vô lí do chỉ có 1 số bằng 0).

Do đó y ≠ 0.

Do đó z = 0.

Khi đó x.(x² + y) - yz = x.(x² + y) - y.0 = x.(x² + y) = 0.

Do x ≠ 0 nên x² + y = 0.

$\Rightarrow$ x² = -y.

Do x ≠ 0 nên x² > 0 khi đó -y > 0 do đó y < 0.

Vậy x là số dương, y là số âm, z bằng 0.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 4)

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Bậc của đơn thức 2²x³y là:

A. 6.

B. 5.

C. 3.

D. 4.

Câu 2. Cho $Δ A B C$ biết BC = 4 cm, AB = 5 cm, AC = 3 cm. Khi đó ta có tam giác ABC:

A. nhọn.

B. vuông tại A.

C. vuông tại B.

D. vuông tại C.

Câu 3. Giá trị có tần số lớn nhất được gọi là:

A. tần số của giá trị đó.

B. mốt của dấu hiệu.

C. số trung bình cộng của dấu hiệu.

D. giá trị lớn nhất.

Câu 4. Tam giác MNP có đường trung tuyến ME và trọng tâm G. Khi đó tỉ số $\frac{M G}{M E}$ bằng:

A. $\frac{2}{3}$

B. $\frac{3}{4}$

C. $\frac{1}{3}$

D. $\frac{3}{2}$

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm) Điều tra về số lượng học sinh nữ của mỗi lớp trong trường A được ghi lại ở bảng sau:

a) Dấu hiệu ở đây là gì? Trường A có bao nhiêu lớp?

b) Trung bình mỗi lớp của trường A có bao nhiêu học sinh nữ?

Bài 2. (2,5 điểm) Cho các đa thức:

A(x) = -5x - 6 + 6x³ - 12;

B(x) = x³ - 5x + 5x³ - 16 - 2x².

a) Thu gọn các đa thức A(x); B(x) và sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến.

b) Tính A(x) + B(x).

c) Tính C(x) = A(x) - B(x) và tìm nghiệm của C(x).

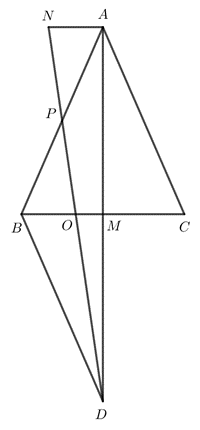
Bài 3. (3,5 điểm) Cho tam giác ABC cân tại A, trung tuyến AM. Qua điểm B vẽ đường thẳng song song với đường thẳng AC, cắt đường thẳng AM tại điểm D.

a) Chứng minh $Δ A M C = Δ D M B .$

b) Chứng minh AB = BD.

c) Gọi P là trung điểm của đoạn thẳng AB, đoạn thẳng PD cắt đoạn thẳng BC tại điểm O. Trên tia đối của tia PO lấy điểm N sao cho PN = PO. Chứng minh điểm O là trọng tâm của $Δ A B D$ và NA = 2OM.

Bài 4. (0,5 điểm) Tìm x để biểu thức P đạt giá trị nhỏ nhất:

P = $|x - 1| + |x - 4| + |x - 6|$ .

Đáp án

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Bậc của đơn thức 2²x³y là:

A. 6.

B. 5.

C. 3.

D. 4.

Hướng dẫn giải

Đáp án đúng là: D

Bậc của đơn thức 2²x³y là 3 + 1 = 4.

Chọn đáp án D.

Câu 2. Cho $Δ A B C$ biết BC = 4 cm, AB = 5 cm, AC = 3 cm. Khi đó ta có tam giác ABC:

A. nhọn.

B. vuông tại A.

C. vuông tại B.

D. vuông tại C.

Hướng dẫn giải

Đáp án đúng là: D

Ta có 5² = 25, 3² + 4² = 9 + 16 = 25.

Do đó AB² = AC² + BC² hay tam giác ABC vuông tại C.

Chọn đáp án D.

Câu 3. Giá trị có tần số lớn nhất được gọi là:

A. tần số của giá trị đó.

B. mốt của dấu hiệu.

C. số trung bình cộng của dấu hiệu.

D. giá trị lớn nhất.

Hướng dẫn giải

Đáp án đúng là: B

Giá trị có tần số lớn nhất được gọi là mốt của dấu hiệu (theo định nghĩa).

Chọn đáp án B.

Câu 4. Tam giác MNP có đường trung tuyến ME và trọng tâm G. Khi đó tỉ số $\frac{M G}{M E}$ bằng:

A. $\frac{2}{3}$

B. $\frac{3}{4}$

C. $\frac{1}{3}$

D. $\frac{3}{2}$

Hướng dẫn giải

Đáp án đúng là: A

Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoàng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh đó nên $\frac{M G}{M E} = \frac{2}{3}$ .

Chọn đáp án A.

II. Tự luận (8,0 điểm)

Bài 1. (1,5 điểm)

Giá trị (x)	16	17	18	19	20	22
Tần số (n)	4	2	5	2	3	4

a) Dấu hiệu là số lượng học sinh nữ của mỗi lớp trong trường A.

Trường A có 4 + 2 + 5 + 2 + 3 + 4 = 20 lớp.

b) Trung bình mỗi lớp của trường A có:

$\frac{16.4 + 17.2 + 18.5 + 19.2 + 20.3 + 22.4}{20}$ = 18,7 ≈ 19 học sinh nữ.

Bài 2. (2,5 điểm) Cho các đa thức:

A(x) = -5x - 6 + 6x³ - 12;

B(x) = x³ - 5x + 5x³ - 16 - 2x².

a) Thu gọn các đa thức A(x); B(x) và sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến.

b) Tính A(x) + B(x).

c) Tính C(x) = A(x) - B(x) và tìm nghiệm của C(x).

a) A(x) = -5x - 6 + 6x³ - 12

A(x) = 6x³ - 5x + (-6 - 12)

A(x) = 6x³ - 5x - 18

B(x) = x³ - 5x + 5x³ - 16 - 2x²

B(x) = (x³ + 5x³) - 2x² - 5x - 16

B(x) = 6x³- 2x² - 5x - 16

b) A(x) + B(x) = 6x³ - 5x - 18 + 6x³- 2x² - 5x - 16

A(x) + B(x) = (6x³+ 6x³) - 2x² + (-5x - 5x) + (-18 - 16)

A(x) + B(x) = 12x³ - 2x² - 10x - 10

c) C(x) = A(x) - B(x)

C(x) = 6x³ - 5x - 18 - (6x³- 2x² - 5x - 16)

C(x) = 6x³ - 5x - 18 - 6x³ + 2x² + 5x + 16

C(x) = (6x³ - 6x³) + 2x² + (-5x + 5x) + (-18 + 16)

C(x) = 2x² - 2

Để C(x) = 0 thì 2x² - 2 = 0

$\Rightarrow$ 2x² = 2

$\Rightarrow$ x² = 1

Trường hợp 1. x²= 1²

$\Rightarrow$ x = 1

Trường hợp 2. x²= (-1)²

$\Rightarrow$ x = -1

Vậy x = 1 hoặc x = -1.

Bài 3. (3,5 điểm)

a) $Δ A B C$ cân tại A có M là trung điểm của BC nên AM vừa là đường trung tuyến, vừa là đường cao của $Δ A B C$ .

Do đó $A D ⊥ B C$ .

Do BD // AC nên $\hat{M B D} = \hat{M C A}$ (2 góc so le trong).

Xét $Δ A M C$ vuông tại M và $Δ D M B$ vuông tại M có:

$\hat{M C A} = \hat{M B D}$ (chứng minh trên).

MB = MC (theo giả thiết).

$\Rightarrow Δ A M C = Δ D M B$ (góc nhọn - cạnh góc vuông)

b) Do $Δ A M C = Δ D M B$ (góc nhọn - cạnh góc vuông) nên MA = MD (2 cạnh tương ướng).

Do đó M là trung điểm của AD.

$Δ A B D$ có M là trung điểm của AD, lại có $B M ⊥ A D$ nên $Δ A B D$ cân tại B.

c) Xét $Δ A B D$ có BM, DP là các đường trung tuyến cắt nhau tại O nên O là trọng tâm của $Δ A B D$ .

Xét $Δ A P N$ và $Δ B P O$ có:

AP = BP (theo giả thiết).

$\hat{A P N} = \hat{B P O}$ (2 góc đối đỉnh).

PN = PO (theo giả thiết).

$\Rightarrow Δ A P N = Δ B P O$ (c - g - c).

$\Rightarrow$ NA = BO (2 cạnh tương ứng).

Do O là trọng tâm của nên BO = $\frac{2}{3}$ BM; OM = $\frac{1}{3}$ BM.

Do đó BO = 2OM.

Mà NA = BO nên NA = 2OM.

Vậy O là trọng tâm của $Δ A B D$ và NA = 2OM.

Bài 5. (0,5 điểm)

P = $|x - 1| + |x - 4| + |x - 6|$

P = $|x - 6| + |x - 1| + |x - 4|$

P = $|6 - x| + |x - 1| + |x - 4|$

Ta có: $|6 - x| + |x - 1| \geq |6 - x + x - 1| = 5$ ; $|x - 4| \geq 0.$

Do đó $|6 - x| + |x - 1| + |x - 4| \geq 5 + 0 = 5.$

Dấu “=” xảy ra khi (6 - x)(x - 1) ≥ 0 và x - 4 = 0.

Suy ra x = 4.

Vậy giá trị nhỏ nhất của P = 5 khi x = 4.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 5)

Bài 1. (2,0 điểm) Thời gian giải một bài toán của 30 học sinh được ghi lại trong bảng sau:

Giá trị (x)	5	7	9	10	12	15
Tần số (n)	3	4	7	9	5	2	N = 30

a) Dấu hiệu ở đây là gì? Tính số trung bình cộng của dấu hiệu.

b) Tìm mốt của dấu hiệu.

Bài 2. (2,0 điểm) Cho đơn thức A = $(\frac{- 2}{3} x^{3} y^{3} z)$ (-6xy³z).

a) Thu gọn, xác định hệ số và bậc của đơn thức A.

b) Tính giá trị của đơn thức A biết x = -1; y = 1; z = $\frac{1}{2}$ .

Bài 3. (2,0 điểm) Cho hai biểu thức

f(x) = -2x⁴- 3x³ + 4x⁴- x² + 5x + 3x² + 5x³ + 6; g(x) = x⁴- x³ + x²- 5x - x³- 2x² + 3.

a) Thu gọn và sắp xếp đa thức f(x) và g(x) theo lũy thừa giảm dần của biến; cho biết bậc; hệ số cao nhất; hệ số tự do của mỗi đa thức.

b) Tìm các đa thức h(x) và k(x), biết:

h(x) = f(x) + g(x); k(x) = f(x) - 2g(x) - 4x².

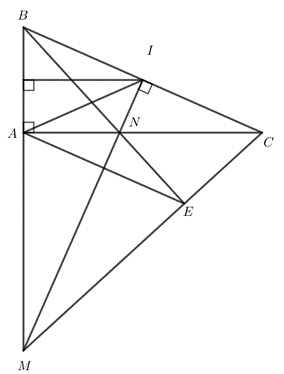
Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A, AC > AB. Đường trung trực của AB cắt BC tại I.

a) Chứng minh rằng $Δ A I B, Δ A I C$ là các tam giác cân.

b) Từ I kẻ đường thẳng d vuông góc với BC, cắt tia BA và AC tại M và N; tia BN cắt CM tại E. Chứng minh rằng $E B ⊥ M C .$

c) Chứng minh rằng các đường thẳng EA và BC song song với nhau.

Bài 5. (0,5 điểm) Tính giá trị của biểu thức T = x³- 2x²- xy² + 2xy + 10x + 10y

biết x + y = 2.

Đáp án

Bài 1. (1,5 điểm)

a) Dấu hiệu là thời gian giải một bài toán của 30 học sinh.

Trung bình cộng của dấu hiệu là:

$\frac{5.3 + 7.4 + 9.7 + 10.9 + 12.5 + 15.2}{30} = \frac{286}{30}$ = 9,5(3) ≈ 9,5.

b) Mốt của dấu hiệu là 10.

Bài 2. (2,0 điểm)

a) A = $(\frac{- 2}{3} x^{3} y^{3} z)$ (-6xy³z)

A = $(\frac{- 2}{3} . - 6)$ .(x³.x).(y³.y³).(z.z)

A = 4x⁴y⁶z²

Hệ số của đơn thức A: 4.

Bậc của đơn thức A: 4 + 6 + 2 = 12.

b) Với x = -1; y = 1; z = $\frac{1}{2}$ thì A = 4.(-1)⁴.1⁶. ${(\frac{1}{2})}^{2}$ = 4.1.1. $\frac{1}{4}$ = 1.

Vậy A = 1 với x = -1; y = 1; z = $\frac{1}{2}$ .

Bài 3. (3,0 điểm)

a) f(x) = -2x⁴- 3x³ + 4x⁴- x² + 5x + 3x² + 5x³ + 6

f(x) = (-2x⁴+ 4x⁴) + (- 3x³+ 5x³) + (- x² + 3x²) + 5x + 6

f(x) = 2x⁴ + 2x³ + 2x² + 5x + 6

Bậc của đa thức f(x): 4.

Hệ số cao nhất của đa thức f(x): 2.

Hệ số tự do của đa thức f(x): 6.

g(x) = x⁴- x³ + x²- 5x - x³- 2x² + 3

g(x) = x⁴ + (- x³- x³) + (x²- 2x²) - 5x + 3

g(x) = x⁴- 2x³- x²- 5x + 3

Bậc của đa thức g(x): 4.

Hệ số cao nhất của đa thức g(x): 1.

Hệ số tự do của đa thức g(x): 3.

b) h(x) = f(x) + g(x)

h(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 + x⁴- 2x³- x²- 5x + 3

h(x) = (2x⁴ + x⁴) + (2x³- 2x³) + (2x²- x²) + (5x - 5x) + (6 + 3)

h(x) = 3x⁴ + x² + 9

k(x) = f(x) - 2g(x) - 4x²

k(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 - 2(x⁴- 2x³- x²- 5x + 3) - 4x²

k(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 - 2x⁴ + 4x³ + 2x² + 10x - 6 - 4x²

k(x) = (2x⁴- 2x⁴) + (2x³ + 4x³) + (2x² + 2x²- 4x²) + (5x + 10x) + (6 - 6)

k(x) = 6x³ + 15x

Bài 4. (3,5 điểm)

a) Do I nằm trên đường trung trực của AB nên AI = BI.

$Δ A I B$ có AI = BI nên cân tại I.

Do đó $\hat{I A B} = \hat{I B A}$ .

Lại có: $\hat{I A B} + \hat{I A C} = 90 °;$ $\hat{I B A} + \hat{I C A} = 90 °$ nên $\hat{I A C} = \hat{I C A}$ .

$Δ A I C$ có $\hat{I A C} = \hat{I C A}$ nên $Δ A I C$ cân tại I.

b) Xét $Δ M B C$ có $C A ⊥ M B;$ $M I ⊥ B C$ .

Mà CA cắt MI tại N nên N là trực tâm của $Δ M B C$ .

Do đó $B N ⊥ M C$ hay $B E ⊥ M C$ .

c) $Δ M B C$ có MI vừa là đường trung tuyến, vừa là đường cao nên $Δ M B C$ cân tại M.

Khi đó MI là đường phân giác của $\hat{B M C} .$

$\Rightarrow \hat{A M N} = \hat{E M N}$ .

Xét $Δ A M N$ vuông tại A và $Δ E M N$ vuông tại E có:

MN chung.

$\hat{A M N} = \hat{E M N}$ (chứng minh trên).

$\Rightarrow Δ A M N = Δ E M N$ (cạnh huyền - góc nhọn).

$\Rightarrow$ MA = ME (2 cạnh tương ứng).

$Δ M A E$ có MA = ME nên $Δ M A E$ cân tại M.

Do đó $\hat{M A E} = \hat{M E A}$ .

Xét $Δ M A E$ có $\hat{M A E} + \hat{M E A} + \hat{A M E} = 180 °$

$\Rightarrow \hat{M A E} = \frac{180 ° - \hat{A M E}}{2}$ (1).

Do $Δ M B C$ cân tại M nên $\hat{M B C} = \hat{M C B}$ .

Xét $Δ M B C$ có $\hat{M B C} + \hat{M C B} + \hat{B M C} = 180 °$

$\Rightarrow 2 \hat{M B C} + \hat{B M C} = 180 °$

$\Rightarrow \hat{M B C} = \frac{180 ° - \hat{B M C}}{2}$ (2).

Từ (1) và (2) suy ra $\hat{M A E} = \hat{M B C}$ .

Mà hai góc này ở vị trí đồng vị nên EA // BC.

Vậy hai đường thẳng EA và BC song song với nhau.

Bài 5. (0,5 điểm)

T = x³- 2x²- xy² + 2xy + 10x + 10y

T = x²(x - 2) - xy(y - 2) + 10(x + y)

T = x².(-y) - xy.(-x) + 10.2

T = -x²y + x²y + 20

T = 20.

Vậy T = 20.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 6)

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Câu 2. Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 3. Tam giác ABC có và . Thứ tự nào sau đây đúng?

A. BC < CA < AB.

B. AB < CA < BC.

C. BC < AB < CA.

D. AB < BC < CA.

Câu 4. Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

II. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức:

P(x) = x⁴ + 3x³- x + $\frac{1}{2}$ - x³- 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴- 2x - 3x + 2x³.

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm dần của biến;

b) Tính P(x) + Q(x); P(x) - Q(x).

Bài 2. (2,0 điểm) Cho các đa thức

A(x) = 12x³ + 2ax + a²

B(x) = 2x²- $|2 a + 3|$ x + a²

Tìm a biết A(1) = B(-2).

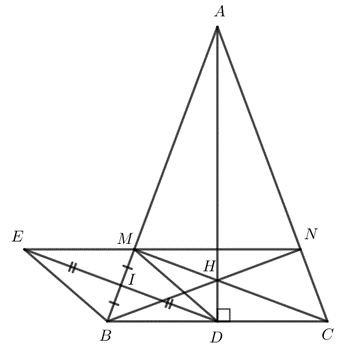
Bài 3. (3,5 điểm) Cho tam giác ABC cân tại A có đường cao AD.

a) Tính BC biết AB = 13 cm và AD = 12 cm.

b) Kẻ DI vuông góc với AB tại I. Lấy điểm M trên cạnh AB sao cho I là trung điểm của đoạn thẳng BM. Chứng minh DM = $\frac{1}{2}$ BC.

c) Gọi H là giao điểm của AD và CM, N là giao điểm của BH và AC. Lấy E là điểm thuộc tia đối của tia ID sao cho ID = IE. Chứng minh 3 điểm E, M, N thẳng hàng.

Bài 4. (0,5 điểm) Tìm tất cả các số nguyên dương x, y thỏa mãn:

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$ .

Đáp án

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Hướng dẫn giải

Đáp án đúng là: B

Ta có x²y²zx = (x².x).y².z = x³y²z ≠ x²y³z.

xy²zxy = (x.x).(y².y).z = x²y³z.

x²zy²z² = x²y².(z.z²) = x²y²z³≠ x²y³z.

x²yxz = (x².x)yz = x³yz ≠ x²y³z.

Do đó chọn đáp án B.

Câu 2. Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

A. 1.

B. 2.

C. 3.

D. 4.

Hướng dẫn giải

Đáp án đúng là: D

Với x = 1 thì P(1) = 1³- 6.1² + 11.1 - 6 = 1 - 6 + 11 - 6 = 0.

Do đó x = 1 là nghiệm của P(x).

Với x = 2 thì P(2) = 2³- 6.2² + 11.2 - 6 = 8 - 6.4 + 22 - 6 = 8 - 24 + 22 - 6 = 0.

Do đó x = 2 là nghiệm của P(x).

Với x = 3 thì P(3) = 3³- 6.3² + 11.3 - 6 = 27 - 6.9 + 33 - 6 = 27 - 54 + 33 - 6 = 0.

Do đó x = 3 là nghiệm của P(x).

Với x = 4 thì P(4) = 4³- 6.4² + 11.4 - 6 = 64 - 96 + 44 - 6 = 6 ≠ 0.

Do đó x = 4 là nghiệm của P(x).

Câu 3. Tam giác ABC có và . Thứ tự nào sau đây đúng?

A. BC < CA < AB.

B. AB < CA < BC.

C. BC < AB < CA.

D. AB < BC < CA.

Hướng dẫn giải

Đáp án đúng là: C

Xét $Δ A B C$ : $\hat{A} + \hat{B} + \hat{C} = 180 °$ .

Khi đó $\hat{C} = 180 ° - \hat{A} - \hat{B}$ = 180^o- 43^o- 69^o = 68^o.

Do 43^o < 68^o < 69^o nên $\hat{A} < \hat{C} < \hat{B}$ .

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn nên $\hat{A} < \hat{C} < \hat{B}$ thì

BC < AB < CA.

Câu 4. Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

Hướng dẫn giải

Đáp án đúng là: C

$Δ A B C$ cân ở A có AD là đường phân giác nên AD vừa là đường phân giác, vừa là đường trung tuyến của $Δ A B C$ .

$Δ A B C$ có hai đường trung tuyến AD và CE cắt nhau tại H nên H là trọng tâm $Δ A B C$ .

Do đó BH chứa trung tuyến kẻ từ đỉnh B.

II. Tự luận (7,0 điểm)

Bài 1. (2,0 điểm)

P(x) = x⁴ + 3x³- x + $\frac{1}{2}$ - x³- 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴- 2x - 3x + 2x³.

a) P(x) = x⁴ + 3x³- x + $\frac{1}{2}$ - x³- 4x

P(x) = x⁴ + (3x³- x³) + (-x - 4x) + $\frac{1}{2}$

P(x) = x⁴ + 2x³- 5x + $\frac{1}{2}$

Q(x) = $\frac{3}{2}$ - 4x³ + x⁴- 2x - 3x + 2x³

Q(x) = x⁴+ (-4x³ + 2x³) + (-2x - 3x) + $\frac{3}{2}$

Q(x) = x⁴- 2x³- 5x + $\frac{3}{2}$

b) P(x) + Q(x) = x⁴ + 2x³- 5x + + x⁴- 2x³- 5x + $\frac{3}{2}$

P(x) + Q(x) = (x⁴ + x⁴) + (2x³- 2x³) + (-5x - 5x) + $(\frac{1}{2} + \frac{3}{2})$

P(x) + Q(x) = 2x⁴- 10x + 1

P(x) - Q(x) = x⁴ + 2x³- 5x + $\frac{1}{2}$ - (x⁴- 2x³- 5x + $\frac{3}{2}$ )

P(x) - Q(x) = x⁴ + 2x³- 5x + $\frac{1}{2}$ - x⁴ + 2x³ + 5x - $\frac{3}{2}$

P(x) - Q(x) = (x⁴- x⁴) + (2x³ + 2x³) + (-5x + 5x) + $(\frac{1}{2} - \frac{3}{2})$

P(x) - Q(x) = 4x³- 1

Bài 2. (2,0 điểm)

A(x) = 12x³ + 2ax + a²

B(x) = 2x²- $|2 a + 3|$ x + a²

Với x = 1 ta có A(1) = 12.1³ + 2.a.1 + a² = 12 + 2a + a².

Với x = -2 ta có B(-2) = 2.(-2)²- $|2 a + 3|$ .(-2) + a² = 9 + 2 $|2 a + 3|$ + a².

Do A(1) = B(-2) nên 12 + 2a + a² = 9 + 2 $|2 a + 3|$ + a².

$\Rightarrow$ 12 + 2a + a²- 9 - a² = 2. $|2 a + 3|$

$\Rightarrow$ (12 - 9) + (a²- a²) + 2a = 2. $|2 a + 3|$

$\Rightarrow$ 3 + 2a = 2. $|2 a + 3|$

Xét 2a + 3 ≥ 0 hay a ≥ $\frac{- 3}{2}$ , khi đó $|2 a + 3|$ = 2a + 3.

Do đó 3 + 2a = 2(2a + 3).

$\Rightarrow$ 3 + 2a = 4a + 6

$\Rightarrow$ 2a - 4a = 6 - 3

$\Rightarrow$ -2a = 3

$\Rightarrow$ a = $\frac{- 3}{2}$ (thỏa mãn)

Xét 2a + 3 < 0 hay a < $\frac{- 3}{2}$ , khi đó $|2 a + 3|$ = -(2a + 3).

Do đó 3 + 2a = -2(2a + 3).

$\Rightarrow$ 3 + 2a = -4a - 6

$\Rightarrow$ 2a + 4a = -6 - 3

$\Rightarrow$ 6a = -9

$\Rightarrow$ a = $\frac{- 9}{6}$

$\Rightarrow$ a = $\frac{- 3}{2}$ (loại)

Vậy a = $\frac{- 3}{2}$ .

Bài 3. (3,5 điểm)

Đề thi Học kì 2 Toán lớp 7 có đáp án đề 6 (ảnh 1)

a) $Δ A B C$ cân tại A có AD là đường cao nên AD cũng là đường trung tuyến.

Do đó D là trung điểm của BC.

Áp dụng định lý Pytago vào $Δ A B D$ vuông tại D ta có:

AD² + BD² = AB²

$\Rightarrow$ 12² + BD² = 13²

$\Rightarrow$ BD²= 169 - 144

$\Rightarrow$ BD² = 25

$\Rightarrow$ BD = 5 cm.

Do D là trung điểm của BC nên BD = $\frac{1}{2}$ BC.

Do đó BC = 10 cm.

b) Xét $Δ D I M$ vuông tại I và $Δ D I M$ vuông tại I có:

ID chung.

IM = IB (theo giả thiết).

$\Rightarrow Δ D I M = Δ D I B$ (2 cạnh góc vuông).

$\Rightarrow$ DM = DB (2 cạnh tương ứng).

Mà DB = $\frac{1}{2}$ BC nên DM = $\frac{1}{2}$ BC.

c) $Δ M B C$ có MD = DB = DC = $\frac{1}{2}$ BC nên $Δ M B C$ vuông tại M.

Do đó $C M ⊥ A B .$

$Δ A B C$ có $A D ⊥ B C;$ $C M ⊥ A B$ .

Mà AD cắt CM tại H nên H là trực tâm của $Δ A B C$ .

Do đó $B H ⊥ A C$ hay $B N ⊥ A C$ .

Do $Δ A B C$ cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B}$ .

Xét $Δ A N B$ vuông tại N và $Δ A M C$ vuông tại M:

$\hat{A}$ chung.

AB = AC (chứng minh trên).

$\Rightarrow Δ A N B = Δ A M C$ (cạnh huyền - góc nhọn).

$\Rightarrow$ AN = AM (2 cạnh tương ứng).

$Δ A M N$ có AN = AM nên $Δ A M N$ cân tại A.

Do đó $\hat{A M N} = \hat{A N M}$ .

Xét $Δ A M N$ có $\hat{A M N} + \hat{A N M} + \hat{M A N} = 180 °$

$\Rightarrow 2 \hat{A M N} + \hat{M A N} = 180 °$

$\Rightarrow \hat{A M N} = \frac{180 ° - \hat{M A N}}{2}$ (1).

Xét $Δ A B C$ có $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$

$\Rightarrow 2 \hat{A B C} + \hat{B A C} = 180 °$

$\Rightarrow \hat{A B C} = \frac{180 ° - \hat{B A C}}{2}$ (2).

Từ (1) và (2) suy ra $\hat{A M N} = \hat{A B C}$ .

Mà hai góc này ở vị trí đồng vị nên MN // BC (3).

Xét $Δ E I M$ và $Δ D I B$ có:

EI = DI (theo giả thiết).

$\hat{E I M} = \hat{D I B}$ (2 góc đối đỉnh).

IM = IB (theo giả thiết).

$\Rightarrow Δ E I M = Δ D I B$ (c - g - c).

$\Rightarrow \hat{E M I} = \hat{D B I}$ (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EM // BD hay EM // BC (4).

Từ (3) và (4) suy ra E, M, N thẳng hàng.

Vậy E, M, N thẳng hàng.

Bài 4. (0,5 điểm)

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$

$\Rightarrow \frac{9}{x y} - \frac{x}{x y} = \frac{2 x y}{x y} + \frac{3 y}{x y}$

Khử mẫu ta được: 9 - x = 2xy + 3y

$\Rightarrow$ 9 = x + 2xy + 3y

$\Rightarrow$ 9 = x(1 + 2y) + $\frac{3}{2}$ .2y

$\Rightarrow$ 9 + $\frac{3}{2}$ = x(1 + 2y) + $\frac{3}{2}$ .2y + $\frac{3}{2}$

$\Rightarrow$ $\frac{18}{2} + \frac{3}{2}$ = x(1 + 2y) + $\frac{3}{2}$ .(2y + 1)

$\Rightarrow$ $\frac{21}{2}$ = (1 + 2y)(x + $\frac{3}{2}$ )

$\Rightarrow$ 21 = (1 + 2y)(2x + 3)

Do x và y các số nguyên dương nên x ≥ 1; y ≥ 1.

Khi đó 2x + 3 ≥ 5; 2y + 1 ≥ 3.

Mà 21 = (1 + 2y)(2x + 3) nên 2x + 3 = 7; 2y + 1 = 3.

+) 2x + 3 = 7

$\Rightarrow$ 2x = 4

$\Rightarrow$ x = 2

+) 2y + 1 = 3

$\Rightarrow$ 2y = 2

$\Rightarrow$ y = 1

Vậy x = 2; y = 1.

Lời giải bài tập lớp 7 sách mới:

ĐỀ THI, GIÁO ÁN, SÁCH LUYỆN THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 7

Bộ giáo án, bài giảng powerpoint, đề thi, sách dành cho giáo viên và khóa học dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi, chuyên đề Cánh diều, Kết nối tri thức, Chân trời sáng tạo...

4.5 (243)

799,000đ

99,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Loạt bài Đề thi Toán lớp 7 năm học 2023-2024 học kì 1, học kì 2 có đáp án của chúng tôi được biên soạn bám sát nội dung sgk Toán 7 giúp bạn giành điểm cao trong các bài thi Toán lớp 7.

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.

Trang trước Trang sau