10 Đề thi Giữa kì 1 Toán 9 Cánh diều (có đáp án, cấu trúc mới)

Với bộ 10 Đề thi Giữa kì 1 Toán 9 Cánh diều năm 2025 theo cấu trúc mới có đáp án và ma trận được biên soạn và chọn lọc từ đề thi Toán 9 của các trường THCS trên cả nước sẽ giúp học sinh lớp 9 ôn tập và đạt kết quả cao trong các bài thi Giữa kì 1 Toán 9.

10 Đề thi Giữa kì 1 Toán 9 Cánh diều (có đáp án, cấu trúc mới)

Xem thử

Chỉ từ 150k mua trọn bộ Đề thi Giữa kì 1 Toán 9 Cánh diều theo cấu trúc mới bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Đề thi Giữa kì 1 Toán 9 năm 2025-2026 (trên cả nước)

• Đề thi Giữa kì 1 Toán 9 THCS&THPT Lương Thế Vinh năm 2025-2026

  Xem đề thi

• Đề thi Giữa kì 1 Toán 9 THCS Lê Quý Đôn (Tp HCM) năm 2025-2026

  Xem đề thi

• Đề thi Giữa kì 1 Toán 9 THCS Nguyễn Trường Tộ năm 2025-2026

  Xem đề thi

• Đề thi Giữa kì 1 Toán 9 THCS&THPT Lê Quý Đôn (Hà Nội) năm 2025-2026

  Xem đề thi

• Đề thi Giữa kì 1 Toán 9 THCS Nghĩa Tân năm 2025-2026

  Xem đề thi

• Đề thi Giữa kì 1 Toán 9 THCS Nguyễn Thị Định năm 2025-2026

  Xem đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1 - Cánh diều

năm 2025

Môn: Toán 9

Thời gian làm bài: phút

(Đề 1)

A. TRẮC NGHIỆM (7,0 điểm)

Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)

Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1. Điều kiện xác định của phương trình $\frac{1}{x-3}-3=\frac{2}{\left(x-3\right)\left(x+4\right)}$ là

A. $x\ne 4;x\ne -3$.

B. $x\ne 3;x\ne -4$.

C. $x\ne 3;x\ne 6$.

D. $x\ne 0;x\ne -3$.

Câu 2. Tổng các nghiệm của phương trình $\left(\frac{1}{3}x-3\right)\left(x+8\right)=0$ là

A. 5.

B. 1.

C. -5.

D. -1.

Câu 3. Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?

A. 2x - 3y = 5.

B. 0x + 2y = 4.

C. 2x - 0y = 3.

D. 0x - 0y = 6.

Câu 4. Nghiệm tổng quát của phương trình 3x + y = 6 là

A. (x; -3x - 6) với $x\in ℝ$ tùy ý.

B. (-3y + 6; y) với $y\in ℝ$ tùy ý.

C. (x; -3x + 6) với $x\in ℝ$ tùy ý.

D. (-3y - 6; y) với $y\in ℝ$ tùy ý.

Câu 5. Cặp số nào sau đây là nghiệm của hệ phương trình $\left\{\begin{array}{l}2x+3y=3\\ -4x-5y=9\end{array}\right.?$

A. (1; 1).

B. (1; -1).

C. (-21; 15).

D. (21; -15).

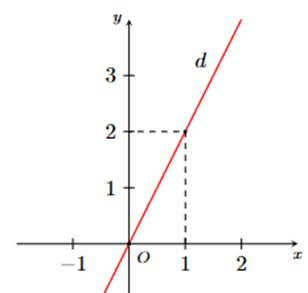
Câu 6. Cho hình vẽ dưới đây:

Đường thẳng d biểu diễn nghiệm của phương trình nào?

A. y = 2x.

B. y = -2x.

C. y = 2x + 1.

D. y = -2x + 1.

Câu 7. Bất đẳng thức m ≤ -8 có thể được phát biểu là

A. m lớn hơn âm 8.

B. m không nhỏ hơn âm 8.

C. m nhỏ hơn âm 8.

D. m không lớn hơn âm 8.

Câu 8. Với ba số a, b và c< 0, các khẳng định sau khẳng định nào đúng?

A. Nếu a > b thì ac > bc.

B. Nếu a > b thì $\frac{a}{c}>\frac{b}{c}.$

C. Nếu a > b thì ac < bc.

D. Nếu a > b thì a + c < b + c.

Câu 9. Tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?

A. AC = AB.tanB.

B. AB = BC.tanB.

C. AC = BC.tanB.

D. AB = AC.tanB.

Câu 10. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Hệ thức nào sau đây là sai?

A. $b=a\cdot \sin B=a\cdot \cos C$.

B. $a=c\cdot \tan B=c\cdot \cot C$.

C. $a^2=b^2+c^2.$.

D. $c=a\cdot \sin C=a\cdot \cos B$.

Câu 11. Cho góc α thỏa mãn 0° < α < 90°. Biết $\tan \alpha =\frac{4}{3}$. Giá trị của $\cot \left(90°-\alpha \right)$ bằng

A. $\frac{3}{4}$.

B. $\frac{4}{3}$.

C. $\frac{5}{3}$.

D. $\frac{5}{4}$.

Câu 12. Cho hình bình hành ABCD có $AC\perp AD$ và $AD=3,5;\widehat{D}=50°$. Hỏi diện tích của hình bình hành là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)

A. 14.

B. 14,6.

C. 14,5.

D. 14,9.

Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)

Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 13. Giải hệ phương trình $\left\{\begin{array}{l}6x-3y=-12\left(1\right)\\ -2x+y=4\left(2\right)\end{array}\right.$ bằng phương pháp thế theo các bước:

a) Từ phương trình (2), ta có y = 2x + 4.

b) Thay y = 2x + 4 vào phương trình (1), ta được 0x = 0.

c) Phương trình 0x = 0 vô nghiệm.

d) Nghiệm tổng quát của hệ phương trình đã cho là (2y + 4; y) với $x\in ℝ$ tùy ý.

Câu 14. Cho bất phương trình m(2x + 1) < 8.

a) Bất phương trình đã cho là bất phương trình bậc nhất ẩn x với $m\in ℝ$ tùy ý.

b) Khi m = 1 bất phương trình đã cho có nghiệm là $x<\frac{7}{2}$.

c) Khi m = -1 bất phương trình đã cho có nghiệm là $x<-\frac{9}{2}$.

d) Khi m = -2 bất phương trình đã cho có nghiệm nguyên lớn nhất là -2.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)

Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Cho phương trình (x -2)(3x + 5) = (2x - 4)(x + 1). Hỏi có bao nhiêu giá trị của x thỏa mãn phương trình đã cho?

Câu 16. Cho hệ phương trình $\left\{\begin{array}{l}x-y=1\\ 3x+y=7\end{array}\right.$ có nghiệm (x; y). Tính tổng x + y.

Câu 17. Số nguyên nhỏ nhất thỏa mãn bất phương trình $x\left(5x+1\right)+4\left(x+3\right)\ge 5x^2$ là bao nhiêu?

Câu 18. Cho góc nhọn α thỏa mãn 0° < α < 70° và biểu thức:

Tính giá trị của biểu thức A.

B. TỰ LUẬN (3,0 điểm)

Bài 1. (1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:

Đại hội Thể thao Đông Nam Á – SEA Games (South East Asian Games) là sự kiện thể thao được tổ chức 2 năm 1 lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là đội chủ nhà của SEA Games 31 diễn ra từ ngày 12/5/2022 đến ngày 23/5/2022. Ở môn bóng đá nam, một bảng đấu có 5 đội A, B, C, D, E thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại).

Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm. Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là  10; 9; 6; 4; 9; 0. Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giữa các đội nào (nếu có)?

Bài 2. (1,5 điểm) Lúc 6 giờ sáng, bạn An đi từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc đỉnh C được mô tả như hình vẽ dưới. Cho biết đoạn AB dài 762 m, $\widehat{A}=4°,\widehat{B}=6°.$

a) Tính chiều cao con dốc (làm tròn kết quả đến hàng đơn vị của mét).

b) Hỏi bạn An đến trường lúc mấy giờ (làm tròn kết quả đến phút)? Biết rằng tốc độ lên dốc là 4 km/h và tốc độ xuống dốc là 19 km/h.

Bài 3. (0,5 điểm) Một công ty du lịch tổ chức một chuyến đi tham quan. Giá vé cho 80 khách đầu tiên là 5 000 000 đồng/người. Nếu có nhiều hơn 40 người đăng ký, mỗi khi có thêm 1 người, giá vé sẽ giảm 50 000 đồng/người cho toàn bộ hành khách. Tính số lượng khách tối ưu để công ty đạt doanh thu cao nhất.

-----HẾT-----

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1 - Cánh diều

năm 2025

Môn: Toán 9

Thời gian làm bài: phút

(Đề 2)

A. TRẮC NGHIỆM (3,0 điểm)

Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn

Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1. Mẫu thức chung khi quy đồng mẫu thức của phương trình $\frac{1}{x-1}+\frac{3}{x^2-1}+x=0$ là

A. (x – 1)².

B. (x + 1)².

C. (x – 1)(x + 1).

D. x(x – 1)(x + 1).

Câu 2. Cho hệ phương trình $\left\{\begin{array}{c}\frac{1}{2}x-\frac{1}{2}y=-1\\ -3x+3y=5\end{array}\right.$. Cho các khẳng định sau:

(i) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 6y = –1.

(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 0x = –1.

(iii) Hệ phương trình đã cho vô nghiệm.

Số khẳng định đúng trong các khẳng định trên là

A. 0.

B. 1.

C. 2.

D. 3.

Câu 3. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?

A. $\sin B=\frac{c}{a}$.

B. $c=\frac{b}{\cot B}$.

C. b = c.cosC.

D. c = b.tanC.

Câu 4. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?

A. AB² = BC² + AC².

B. sinC = cosB.

C. cotB – tanB = 0.

D. $\cot C=\frac{AC}{AB}$.

Phần 2. Câu trắc nghiệm đúng sai

Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 5. Cho bất đẳng thức –5a > 3.

a) Số a có giá trị là một số âm.

b) Biểu thức 3 – 5a có giá trị là một số dương.

c) Biểu thức $a+\frac{3}{5}$ có giá trị là một số dương.

d) Biểu thức –10a – 10 có giá trị là một số âm.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 6. Tìm nghiệm của hệ phương trình $\left\{\begin{array}{c}\frac{3}{2x-y}-\frac{6}{x+y}=-1\\ \frac{1}{2x-y}-\frac{1}{x+y}=0\end{array}\right.$.

Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và đường cao AH = 3 cm. Tính số đo góc C (làm tròn kết quả đến phút).

B. TỰ LUẬN (7,0 điểm)

Bài 1. (2,5 điểm)

1. Giải các phương trình sau:

a) 4x(x + 3) – 3x – 9 = 0.

b) $\frac{x+2}{x-2}=\frac{x-2}{x+2}+\frac{16}{x^2-4}$.

2. Giải các bất phương trình sau:

a) 3x – 8 < 4x – 12.

b) 3(x – 2) – 5 > 3(2x – 1).

c) $\frac{4x-1}{2}+\frac{6x-19}{6}\ge \frac{9x-11}{3}$.

Bài 2. (2,0 điểm)

1. Xác định a và b sao cho hệ phương trình $\left\{\begin{array}{l}ax+2by=-18\\ bx-3ay=-3\end{array}\right.$ nhận cặp số (–3; 2) làm nghiệm.

2. Giải bài toán sau bằng cách lập hệ phương trình:

Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.

Bài 3. (2,0 điểm)

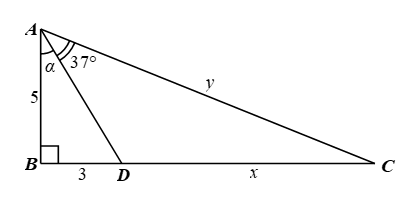
1. Cho hình vẽ bên. Tính số đo góc α và các độ dài x, y (góc làm tròn đến độ và độ dài làm tròn đến hàng phần trăm).

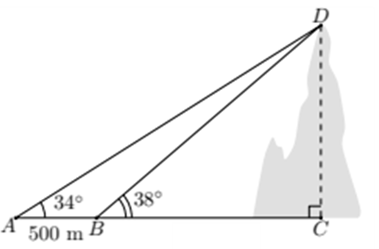
2. Tính chiều cao của một ngọn núi (kết quả làm tròn đến hàng đơn vị), biết tại hai điểm A, B cách nhau 500 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34° và 38° (hình vẽ).

Bài 4. (0,5 điểm) Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo, chứng minh rằng:

$S_{ABCD}=\frac{1}{2}AC\cdot BD\cdot \sin \alpha .$

-----HẾT-----

ĐÁP ÁN

A. TRẮC NGHIỆM (3,0 điểm)

Bảng đáp án trắc nghiệm:

B. TỰ LUẬN (7,0 điểm)

Bài 1. (2,5 điểm)

Hướng dẫn giải

1. a) 4x(x + 3) – 3x – 9 = 0         4x(x + 3) – 3(x + 3) = 0         (x + 3)(4x – 3) = 0         x + 3 = 0 hoặc 4x – 3 = 0         x = –3 hoặc x = $\frac{3}{4}$. Vậy phương trình đã cho có hai nghiệm là x = –3; x = $\frac{3}{4}$.	1. b) Điều kiện xác định: x ≠ 2, x ≠ –2. $\frac{x+2}{x-2}=\frac{x-2}{x+2}+\frac{16}{x^2-4}$ $\frac{{\left(x+2\right)}^2}{\left(x-2\right)\left(x+2\right)}=\frac{{\left(x-2\right)}^2}{\left(x-2\right)\left(x+2\right)}+\frac{16}{\left(x-2\right)\left(x+2\right)}$ (x + 2)2 = (x – 2)2 + 16 x2 + 4x + 4 = x2 – 4x + 4 + 16 8x = 16   x = 2 (không thỏa mãn điều kiện) Vậy phương trình đã cho vô nghiệm.
2. a) 3x – 8 < 4x – 12         3x – 4x < – 12 + 8         –x < –4         x > 4. Vậy nghiệm của bất phương trình đã cho là x > 4. 2. b) 3(x – 2) – 5 > 3(2x – 1)         3x – 6 – 5 > 6x – 3         3x – 6x > – 3 + 6 + 5         –3x > 8         x < $-\frac{8}{3}$. Vậy nghiệm của bất phương trình đã cho là x < $-\frac{8}{3}$.	2. c) $\frac{4x-1}{2}+\frac{6x-19}{6}\ge \frac{9x-11}{3}$         $\frac{3\left(4x-1\right)}{6}+\frac{6x-19}{6}\ge \frac{2\left(9x-11\right)}{6}$         3(4x – 1) + 6x – 19 ≥ 2(9x – 11)         12x – 3 + 6x – 19 ≥ 18x – 22         12x + 6x – 18x ≥ – 22 + 3 + 19         0x ≥ 0 Vậy nghiệm của bất phương trình đã cho là x ∈ ℝ.

Bài 2. (2,0 điểm)

Hướng dẫn giải

1. Để hệ phương trình $\left\{\begin{array}{l}ax+2by=-18\\ bx-3ay=-3\end{array}\right.$ nhận cặp số (–3; 2) làm nghiệm thì x = –3 và y = 2 thỏa mãn hệ phương trình. Khi đó, ta có $\left\{\begin{array}{l}a\cdot \left(-3\right)+2b\cdot 2=-18\\ b\cdot \left(-3\right)-3a\cdot 2=-3\end{array}\right.$hay $\left\{\begin{array}{l}-3a+4b=-18\\ -6a-3b=-3\end{array}\right.$.

Nhân hai vế của phương trình thứ hai với $\frac{3}{4}$ ta được hệ phương trình mới $\left\{\begin{array}{l}-3a+4b=-18\\ -8a-4b=-4\end{array}\right.$.

Cộng từng vế hai phương trình của hệ trên, ta được:

–11a = –22 suy ra a = 2.

Thay a = 2 vào phương trình –3a + 4b = –18, ta được:

–3.2 + 4b = –18, suy ra 4b = –12 nên b = –3.

Vậy a = 2 và b = –3.

2. Gọi x (km/h) là vận tốc dự định của ôtô và y (giờ) là thời gian dự định của ôtô để đi hết quãng đường AB (x > 10, y > 3).

– Quãng đường AB là xy (km).

– Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Khi đó, ta có:

  ⦁ Vận tốc của ôtô lúc này là: x + 10 (km/h).

  ⦁ Thời gian ôtô đi hết quãng đường AB là: y – 3 (giờ).

  ⦁ Quãng đường AB là: (x + 10)(y – 3) (giờ).

Ta có phương trình: (x + 10)(y – 3) = xy

                                 xy – 3x + 10y – 30 = xy

                                 – 3x + 10y = 30  (1)

– Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi muộn hơn so với dự định là 5 giờ. Khi đó, ta có:

  ⦁ Vận tốc của ôtô lúc này là: x – 10 (km/h).

  ⦁ Thời gian ôtô đi hết quãng đường AB là: y + 5 (giờ).

  ⦁ Quãng đường AB là: (x – 10)(y + 5) (giờ).

Ta có phương trình: (x – 10)(y + 5) = xy

                                 xy + 5x – 10y – 50 = xy

                                 5x – 10y = 50  (2)

Từ phương trình (1) và phương trình (2) ta có hệ phương trình: $\left\{\begin{array}{l}-3x+10y=30\\ 5x-10y=50\end{array}\right.$

Cộng từng vế hai phương trình của hệ, ta được: 2x = 80 suy ra x = 40 (thỏa mãn).

Thay x = 40 vào phương trình (1), ta được:

–3.40 + 10y = 30 hay 10y = 150 suy ra y = 15 (thỏa mãn).

Vậy vận tốc dự định của ôtô là 40 (km/h) và thời gian ôtô đi hết quãng đường AB là 15 (giờ).

Bài 3. (2,0 điểm)

Hướng dẫn giải

1. Xét ∆ABD vuông tại B, ta có:

$\tan \widehat{BAD}=\frac{BD}{AB}=\frac{3}{5}$, từ đó ta tìm được $\alpha =\widehat{BAD}\approx 31°$.

Suy ra $\widehat{BAC}=\widehat{BAD}+\widehat{DAC}\approx 31°+37°=68°$.

Xét ∆ABC vuông tại B, ta có:

⦁ BC = $AB\cdot \tan \widehat{BAC}$ $\approx 5\cdot \tan 68°\approx \mathrm{12,38}$, suy ra x = CD = BC – BD ≈ 12,38 – 3 = 9,38;

⦁ AB = $AC\cdot \cos \widehat{BAC}$ suy ra y = AC = $\frac{AB}{\cos \widehat{BAC}}\approx \frac{5}{\cos 68°}\approx \mathrm{13,35}$.

Vậy α ≈ 31°; x ≈ 9,38 và y ≈ 13,35.

2. Đặt: BC = x (m), khi đó AC = AB + BC = 500 + x (m).

Xét ∆ACD vuông tại C, ta có: CD = $AC\cdot \text{tan}\widehat{CAD}$ = (500 + x).tan34°.

Xét ∆BCD vuông tại C ta có: CD = $BC\cdot \text{tan}\widehat{CBD}$ = x.tan38°.

Do đó, ta có: (500 + x).tan34° = x.tan38°

                       500.tan34° + x.tan34° = x.tan38°

                       x.tan38° – x.tan34° = 500.tan34°

                       x(tan38° – tan34°) = 500.tan34°

                       x = $\frac{500\cdot \text{tan}34°}{\text{tan}38°-\text{tan}34°}\approx 3\mathrm{158,5}$ (m).

Suy ra CD = x.tan38° ≈ 3 158,5 . tan 38° ≈ 2 468 (m).

Vậy ngọn núi cao khoảng 2 468 mét.

Bài 4. (0,5 điểm)

Hướng dẫn giải

Gọi E là giao điểm của hai đường chéo AC và BD. Kẻ đường cao AH xuống BD và đường cao DK xuống AC. Xét ∆AEH vuông tại H có: AH = AE.sinα. Do đó $S_{ADE}=\frac{1}{2}DE\cdot AH=\frac{1}{2}DE\cdot AE\cdot \sin \alpha$. Ta có: $\frac{S_{ADE}}{S_{ADC}}=\frac{\frac{1}{2}DK\cdot AE}{\frac{1}{2}DK\cdot AC}=\frac{AE}{AC}$ Suy ra $S_{ADC}=\frac{AC}{AE}\cdot S_{ADE}$ = $\frac{AC}{AE}\cdot \frac{1}{2}DE\cdot AE\cdot \sin \alpha$ = $\frac{1}{2}DE\cdot AC\cdot \sin \alpha .$ Tương tự, ta có: $S_{ABC}=\frac{1}{2}BE\cdot AC\cdot \sin \alpha$ Khi đó: SABCD = SADC + SABC = $\frac{1}{2}$DE.AC.sinα = $\frac{1}{2}$DE.AC.sinα.                                             = $\frac{1}{2}$AC.(DE + BE).sinα = $\frac{1}{2}$AC.BD.sinα. Vậy SABCD = $\frac{1}{2}$AC.BD.sinα.

-----HẾT-----

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 9 năm 2025 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

Tham khảo đề thi Toán 9 Cánh diều có đáp án hay khác:

• Đề thi Học kì 1 Toán 9 Cánh diều (có đáp án)

• Đề thi Giữa kì 2 Toán 9 Cánh diều (có đáp án)

• Đề thi Học kì 2 Toán 9 Cánh diều (có đáp án)

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---