15+ Đề thi Học kì 1 Toán 9 Cánh diều (cấu trúc mới, có đáp án)
Với bộ 15+ Đề thi Học kì 1 Toán 9 Cánh diều năm 2026 theo cấu trúc mới có đáp án và ma trận được biên soạn và chọn lọc từ đề thi Toán 9 của các trường THCS trên cả nước sẽ giúp học sinh lớp 9 ôn tập và đạt kết quả cao trong các bài thi Học kì 1 Toán 9.
15+ Đề thi Học kì 1 Toán 9 Cánh diều (cấu trúc mới, có đáp án)
Chỉ từ 150k mua trọn bộ Đề thi Học kì 1 Toán 9 Cánh diều theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Đề thi Học kì 1 Toán 9 Cánh diều (Giáo viên VietJack)
50+ Đề thi Toán 9 Cuối kì 1 năm 2025-2026 (cả nước)
Đề thi Học kì 1 Toán 9 trường THCS Đỗ Đăng Tuyển (Đà Nẵng) năm 2025-2026
Đề thi Học kì 1 Toán 9 trường THCS Phạm Ngọc Thạch (Tp. HCM) năm 2025-2026
Đề thi Học kì 1 Toán 9 phường Ba Đình (Hà Nội) năm 2025-2026
Đề thi Học kì 1 Toán 9 phường Giảng Võ (Hà Nội) năm 2025-2026
Đề thi Học kì 1 Toán 9 trường THPT chuyên Hà Nội – Amsterdam năm 2025-2026
Đề thi Học kì 1 Toán 9 trường THCS Đống Đa (Hà Nội) năm 2025-2026
Đề thi Học kì 1 Toán 9 trường Tạ Quang Bửu (Hà Nội) năm 2025-2026
Đề thi Học kì 1 Toán 9 trường Marie Curie (Hà Nội) năm 2025-2026
Đề thi Học kì 1 Toán 9 trường THCS Đông Thạnh (Tp. HCM) năm 2025-2026
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề 1)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Điều kiện xác định của phương trình là
A. x ≠ -4; x ≠ 2.
B. x ≠ 4; x ≠ -2.
C. x ≠ 4; x ≠ 2.
D. x ≠ 4; x ≠ 2.
Câu 2. Trong các hệ thức sau, hệ thức nào không phải là phương trình bậc nhất hai ẩn?
A. x - 2y = 3.
B. 0x + 3y = 1.
C. 0x - 0y = 5.
D. 2x - 0y = 4.
Câu 3. Trong các hệ phương trình dưới đây, đâu là phương trình bậc nhất hai ẩn?
A.
B.
C.
D.
Câu 4. Cho a bất kì. Kết quả so sánh nào dưới đây là đúng?
A. a - 4 > a - 5.
B. a - 3 < a - 4.
C. a - 2 ≤ a - 4.
D. a - 7 ≥ a - 9.
Câu 5. Phát biểu “ x không lớn hơn ” được viết là
A.
B.
C.
D.
Câu 6. Điều kiện xác định của căn thức là
A. x ≥ 1.
B. x > 1.
C. x < 1.
D. x ≤ 1.
Câu 7. Biểu thức bằng
A. 3 - 2x.
B. 2x - 3.
C. |2x - 3|
D. 2x - 3 và -2x + 3
Câu 8. Rút gọn ta được
A. |1 - x|.
B. 1 - x.
C. x - 1.
D. Cả A, B, C đều sai.
Câu 9. Cho tam giác ABC vuông tại A có AC = 3; AB = 4; BC = 5. Khi đó tanC bằng
A.
B.
C.
D.
Câu 10. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây là sai?
A. sinB = cosC.
B. cosB = sinC.
C. cotB = tanC.
D.
Câu 11. Góc ở tâm chắn cung 160° có số đo bằng bao nhiêu?
A. 200°.
B. 160°.
C. 80°.
D. 20°.
Câu 12. Cho đường tròn (O; 4 cm) và (O'; 3 cm) có OO' = 5 cm. Vị trí tương đối của hai đường tròn đã cho là
A. tiếp xúc trong.
B. cắt nhau.
C. tiếp xúc ngoài.
D. đựng nhau.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Lan có một dung dịch nước muối sinh lí có nồng độ 1,5% và một dung dịch nước cất không chứa muối (nồng độ 0%). Lan cần pha trộn dung dịch để thu được 1 lít (1000 ml) dung dịch nước muối dinh lí súc miệng có nồng độ 0,9%. Gọi x (ml) là thể tích dung dịch nước muối 1,5% và y (ml) là thể tích nước cất 0% (x, y > 0).
a) Phương trình biểu diễn tổng thể tích dung dịch là x + y = 1000.
b) Phương trình biểu diễn lượng muối trong dung dịch ban đầu là 0,015x + y = 900.
c) Hệ phương trình biểu diễn bài toán là .
d) Lan cần pha 600 ml dung dịch nước muối 1,5% và 400 ml dung dịch nước cốt 0% để được dung dịch mong muốn.
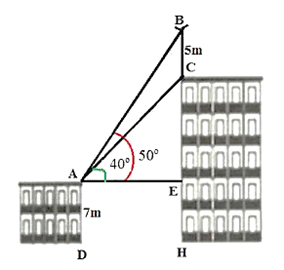
Câu 14. Trên nóc của một tòa nhà có một cột ăng – ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và đỉnh C của một cột ăng – ten dưới góc 50° và 40 ° so với phương nằm ngang.
a)
b)
c) .
d) Chiều cao của tòa nhà lớn hơn 24 m.
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Có bao nhiêu giá trị của x thỏa mãn phương trình ?
Câu 16. Tìm giá trị nguyên nhỏ nhất của x thỏa mãn bất phương trình .
Câu 17. Tính giá trị của biểu thức tại x = 25. (Kết quả ghi dưới dạng số thập phân)
Câu 18. Mặt đĩa CD có dạng vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là 4 cm và 6 cm. Hình vành khuyên đó có diện tích bằng bao nhiêu centimet vuông? (Kết quả làm tròn đến hàng phần mười)
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Cho biểu thức với x > 0 và x ≠ 1.
a) Chứng minh rằng
b) Tìm các giá trị của x để .
Bài 2. (1,5 điểm) Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O') đường kính BC.
a) Gọi H là trung điểm của AC. Vẽ dây DE của đường tròn (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
b) DC cắt đường tròn (O') tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.
c) Chứng minh rằng HF là tiếp tuyến của đường tròn (O').
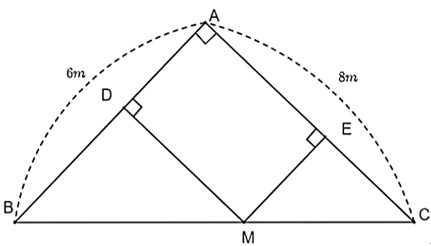
Bài 3. (0,5 điểm) Một người đào ao cá trên thửa ruộng dạng hình tam giác vuông ABC tại A có độ dài các cạnh góc vuông AB = 6 m, AC = 8 m. Một chiếc máy xúc ở vị trí điểm M di chuyển trên bờ BC. Gọi MD và ME là khoảng cách từ M đến bờ AB, AC, Người đó đào được ao là tứ giác ADME. Tính diện tích lớn nhất của ao cá mà người đó có thể đào.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề 2)
A. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Điều kiện xác định của phương trình là
A. x ≠ 7 và x ≠ –4.
B. x ≠ 4.
C. x ≠ –7 và x ≠ 4.
D. x ≠ –7.
Câu 2. Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
A. .
B. .
C. .
D. .
Câu 3. Tất cả các nghiệm của phương trình 4x + 2y – 6 = 0 được biểu diễn bởi đường thẳng nào sau đây?
A. y = 2x – 3.
B. y = –2x + 3.
C. y = 3x + 2.
D. y = 4x – 6.
Câu 4. Bất đẳng thức n ≤ 3 có thể được phát biểu là
A. n lớn hơn 3.
B. n nhỏ hơn 3.
C. n không lớn hơn 3.
D. n không nhỏ hơn 3.
Câu 5. Nghiệm của bất phương trình 5x – 4 – 3(2x – 9) ≤ 5x – 8 là
A. .
B. .
C. .
D. .
Câu 6. Với mọi số a, ta luôn có:
A. .
B. .
C. .
D. .
Câu 7. Với hai số a < 0, b > 0, biểu thức có giá trị là
A. –a2.
B. a2.
C. a2b2.
D. –a2b2.
Câu 8. Cho β là góc nhọn bất kì. Khẳng định nào sau đây đúng?
A. .
B. .
C. .
D. .
Câu 9. Cho tam giác ABC vuông tại C có AC = 1,2 cm, AB = 1,5 cm. Tỉ số lượng giác tanB là
A. .
B. .
C. .
D. .
Câu 10. Cho hai đường tròn (O; R) và (O’; r) với R > r cắt nhau tại hai điểm phân biệt và OO’ = d. Chọn khẳng định đúng?
A. d > R + r.
B. d = R – r.
C. d < R – r.
D. R – r < d < R + r.
Câu 11. Khẳng định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo góc ở tâm cùng chắn một cung.
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
Câu 12. Một công viên có hồ nước hình tròn với bán kính 50 m. Xung quanh hồ, người ta xây một lối đi hình vành khăn có chiều rộng 5 m (hình vẽ). Diện tích lối đi của công viên là
A. 252π m2.
B. 25π m2.
C. 5π m2.
D. 525π m2.
B. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Cho hai biểu thức và với x > 0, x ≠ 1.
a) Tính giá trị của biểu thức A khi x = 16.
b) Rút gọn biểu thức B.
c) Xét biểu thức P = AB. Tìm tất cả các giá trị của x sao cho P nhận giá trị nguyên.
Bài 2. (2,0 điểm)
1. Giải các phương trình và bất phương trình sau:
a) .
b) .
2. Giải bài toán sau bằng cách lập hệ phương trình:
Có hai loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng chứa 66% sắt.
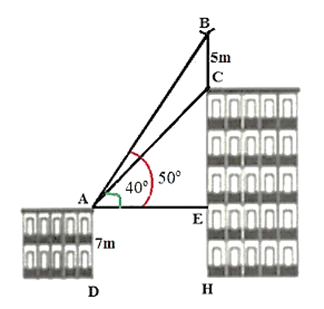
Bài 3. (1,0 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và đỉnh C của một cột ăng – ten dưới góc 50° và 40° so với phương nằm ngang. Tính chiều cao của tòa nhà.
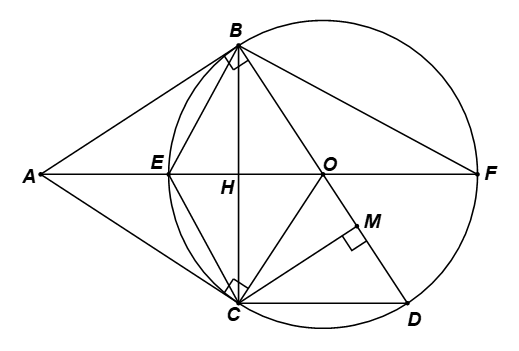
Bài 4. (2,0 điểm) Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ A tiếp xúc với đường tròn tại B và C. Gọi H là giao điểm của OA và BC, kẻ đường kính BD của đường tròn (O), hạ CM ⊥ BD tại M. Tia AO cắt đường tròn (O) tại E, F.
a) Chứng minh rằng ∆CMD ᔕ ∆ACO.
b) Chứng minh rằng BE là phân giác của .
c) Cho và AH = 4 cm. Tính diện tích hình quạt giới hạn bởi các bán kính OB, OC và cung nhỏ BC.
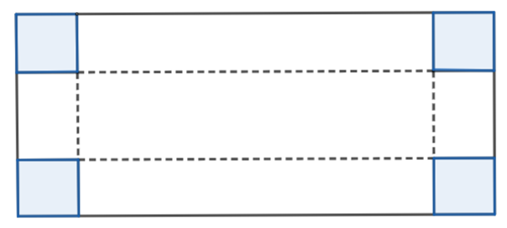
Bài 5. (0,5 điểm) Một tấm bìa cứng hình chữ nhật có chiều dài là 50 cm và chiều rộng là 30 cm. Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh x (cm) và xếp phần còn lại thành một hình hộp không nắp. Tìm x để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.
-----HẾT-----
ĐÁP ÁN & HƯỚNG DẪN
A. TRẮC NGHIỆM (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
B |
A |
B |
C |
A |
B |
B |
C |
B |
D |
D |
D |
B. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
Hướng dẫn giải
a) Thay x = 16 (thỏa mãn điều kiện) vào biểu thức A, ta được:
A = .
Vậy khi x = 16.
2) Với x > 0, x ≠ 1, ta có:
Vậy với x > 0, x ≠ 1 thì B = .
2) – Với x > 0, x ≠ 1, ta có:
P = A.B = = =
Với x > 0, x ≠ 1, ta cũng có:
⦁ nên , do đó suy ra
⦁ nên , do đó suy ra
Khi đó, –2 < P < 1.
– Để P nhận giá trị nguyên thì P = –1 hoặc P = 0.
⦁ Với P = –1, ta có , suy ra , nên , do đó , hay (thỏa mãn).
⦁ Với P = 0, ta có , suy ra , nên , do đó , hay x = 4 (thỏa mãn).
Vậy .
Bài 2. (2,0 điểm)
Hướng dẫn giải
1. Giải các phương trình, bất phương trình sau:
2. Gọi x, y (tấn) lần lượt là khối lượng quặng chứa 75% sắt và 50% sắt (x, y > 0).
Theo đề, tổng khối lượng quặng là 25 tấn nên ta có: x + y = 25. (1)
Khối lượng sắt trong 25 tấn quặng chứa 66% sắt là: 25.66% = 16,5 (tấn).
Khối lượng sắt trong x (tấn) quặng chứa 75% sắt là: x.75% = 0,75x (tấn).
Khối lượng sắt trong y (tấn) quặng chứa 50% sắt là: y.50% = 0,5y (tấn).
Do đó, ta có phương trình: 0,75x + 0,5y = 16,5. (2)
Từ (1) và (2) ta có hệ phương trình: .
Từ phương trình (1), suy ra y = 25 – x.
Thay y = 25 – x vào phương trình (2) ta được:
0,75x + 0,5(25 – x) = 16,5
0,75x + 12,5 – 0,5x = 16,5
0,25x = 4
x = 16 (thỏa mãn).
Thay x = 16 vào phương trình y = 25 – x, ta được y = 9 (thỏa mãn).
Vậy cần trộn 16 tấn quặng chứa 75% sắt và 9 tấn quặng chứa 50% sắt để được 25 tấn quặng chứa 66% sắt.
Bài 3. (1,0 điểm)
Hướng dẫn giải
Chiều cao của tòa nhà chính là độ dài đoạn thẳng BH.
Xét tam giác CAE vuông tại E, ta có:
CE = AE. = AE.tan 40° (m) (1).
Xét tam giác BAE vuông ở E, ta có:
BE = AE. = AE.tan 50° (m) (2).
Từ (1) và (2) suy ra BC = BE - CE = AE tan 50° - AE tan 40°
BC = AE (tan 50° - tan 40°)
5 = AE (tan 50° - tan 40°)
AE = (m)
Suy ra CE = = ≈ 11,9 (m).
Chiều cao của tòa nhà là: 5 + 11,9 + 7 ≈ 23,9 (m).
Vậy tòa nhà cao khoảng 23,9 mét.
Bài 4. (2,0 điểm)
Hướng dẫn giải
a) Ta có: AB, AC là hai tiếp tuyến của đường tròn (O), suy ra OA là đường phân giác của (tính chất) nên .
Xét đường tròn (O), ta có: (góc nội tiếp và góc ở tâm cùng chắn cung BC)
Do đó, .
Xét ∆CMD và ∆ACO có:
và (do )
Do đó ∆CMD ᔕ ∆ACO (g.g).
b) Xét đường tròn (O), ta có: (góc nội tiếp chắn nửa đường tròn).
Ta có nên
Suy ra .
Lại có: (vì ∆BOF cân tại O do OB = OF), suy ra (1)
Mà (hai góc nội tiếp cùng chắn cung EC của đường tròn tâm O) (2)
Từ (1) và (2) suy ra . (3)
Mặt khác, AB = AC (tính chất hai tiếp tuyến cắt nhau) và OB = OC
Suy ra OA là đường trung trực của BC mà E ∈ OA, suy ra EB = EC.
Do đó ∆EBC cân tại E nên . (4)
Từ (3) và (4) suy ra nên BE là tia phân giác của góc B trong tam giác ABH.
Vậy BE là phân giác của .
c) Theo câu a, ∆ACO ᔕ ∆CMD (g.g), suy ra .
Suy ra .
Do đó, hay .
Xét ∆AHC vuông tại H, có:
Suy ra AC = (cm).
Xét ∆ACO vuông tại C, có: OC = (cm).
Diện tích hình quạt giới hạn bởi các bán kính OB, OC và cung nhỏ BC là:
S = (cm2).
Bài 5. (0,5 điểm)
Hướng dẫn giải
Diện tích tấm bìa hình chữ nhật này là: 50 . 30 = 1 500 (cm2).
Chiều dài sau khi cắt tấm bìa là: 50 – 2x (cm).
Chiều rộng sau khi cắt tấm bìa là: 30 – 2x (cm).
Diện tích xung quanh của hộp là:
2x(50 – 2x + 30 – 2x) = 2x(80 – 4x) = –8x2 +160x (cm2).
Để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất thì –8x2 +160x đạt giá trị lớn nhất.
Ta có: –8x2 +160x = –8(x2 – 20x + 100) + 800 = –8(x – 10)2 + 800.
Với mọi x > 0 ta có: –8(x – 10)2 ≤ 0 nên –8(x – 10)2 + 800 ≤ 800.
Dấu “=” xảy ra khi x – 10 = 0 hay x = 10.
Vậy diện tích xung quanh hình hộp chữ nhật là 800 cm2 khi x = 10 cm.
-----HẾT-----
................................
................................
................................
Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 9 năm 2026 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:
Tham khảo đề thi Toán 9 Cánh diều có đáp án hay khác:
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Đề thi các môn học lớp 9 năm 2025 học kì 1 và học kì 2 được biên soạn bám sát cấu trúc ra đề thi mới Tự luận và Trắc nghiệm giúp bạn giành được điểm cao trong các bài thi lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)











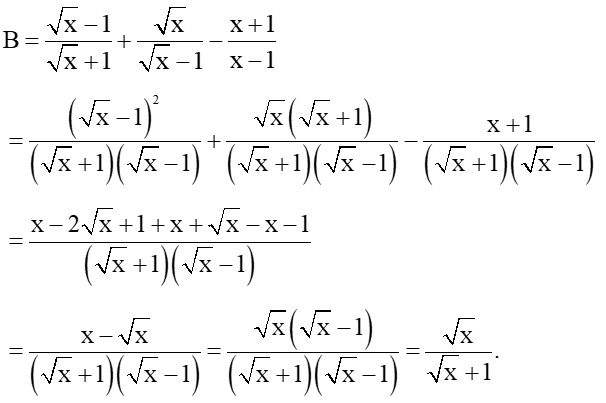




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

