Đáp án Đề kiểm tra Hình học 11 Chương 3 (Đề 2)

---

---

Đáp án Đề kiểm tra Hình học 11 Chương 3 (Đề 2)

Xem lại Đề kiểm tra Hình học 11 Chương 3 (Đề 2)

Phần trắc nghiệm

Câu 1: Đáp án C

Lời giải:

Ta có:

a. Sai, bởi chúng có thể cắt nhau.

b. Sai, bởi chúng có thể song song với nhau.

c. Đúng, dựa trên khái niệm về góc giữa hai đường thẳng.

d. Sai, bởi chúng có thể cắt nhau.

Câu 2: Đáp án D

Câu 3: Đáp án B

Câu 4: Đáp án A

Câu 5: Đáp án D

Lời giải:

Ta lần lượt có:

a. Với (A) thì N đúng là trung điểm của một đoạn MP, do đó (A) đúng.

b. Với (B) đúng vì đó chính là quy tắc trung điểm.

c. Với (C) đúng vì thỏa mãn định lí về sự đồng phẳng của ba vecto trong không gian.

d. Với (D) thì bằng quy tắc ba điểm ta nhận thấy đẳng thức: 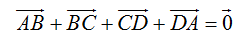đúng với mọi điểm A, B, C, D nên cũng đúng với tứ diện ABCD.

Do đó (D) là sai.

Câu 6: Đáp án D

Câu 7: Đáp án D

Câu 8: Đáp án A

Câu 9: Đáp án A

Lời giải:

Ta lần lượt có hai cách biểu diễn:

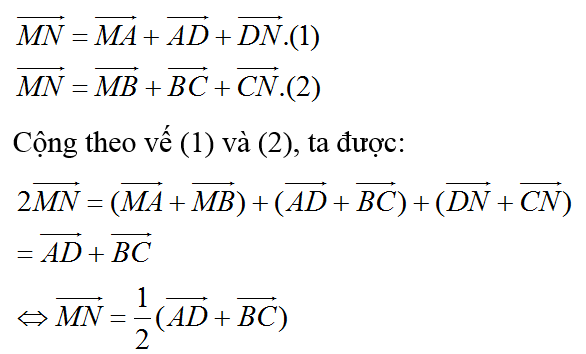
Câu 10: Đáp án C

Lời giải:

Ta có: 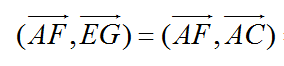bởi ∆AFC là tam giác đều.

Câu 11: Đáp án B

Lời giải:

Trong ∆OSA vuông tại O, ta có:

SO² = SA² – AO² = a² - (a√2/2)² = a/2

=> SO = a√2/2 .

Câu 12: Đáp án C

Lời giải:

Trong ∆ABD có ∠A = 60° nên nó là tam giác đều, do đó:

BD = a, AI = a√3/2 => AC = a√3

Trong ∆SAC vuông tại C, ta có:

SA² = SC² + AC² =

Vì hai tam giác AKI và ACS đồng dạng, nên:

bởi ∆AFC là tam giác đều.

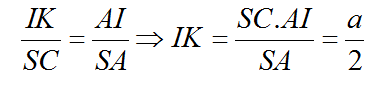
Phần tự luận

Bài 1:

Lời giải:

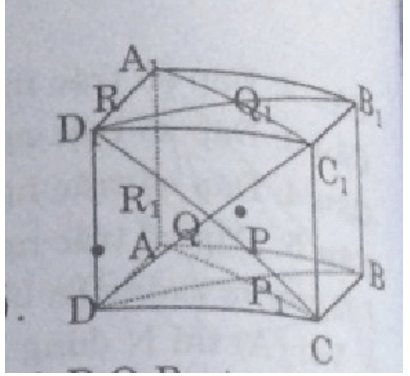bởi ∆AFC là tam giác đều.

a. Ta có:

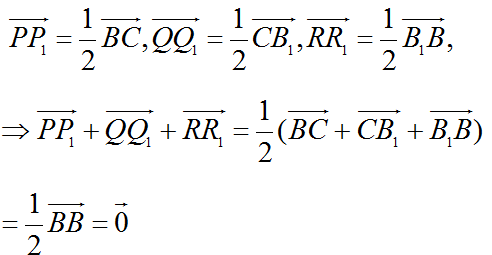bởi ∆AFC là tam giác đều.

b. Gọi G, G1 theo thứ tự là trọng tâm các tam giác PQR và P1Q1R1, ta có:

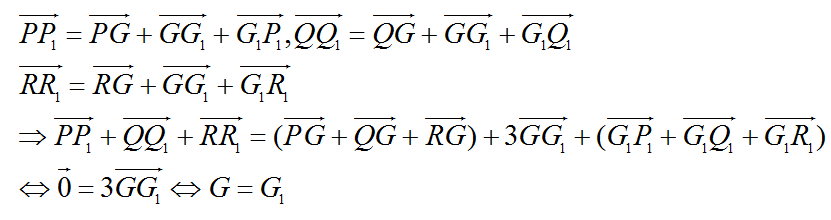bởi ∆AFC là tam giác đều.

Bài 2:

Lời giải:

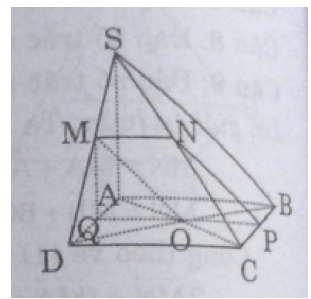bởi ∆AFC là tam giác đều.

a. Ta lần lượt thực hiện:

Xác định mặt phẳng α. Trong (SAD) dựng Mx // SA và cắt AD tại Q là trung điểm của AD, ta có:

MQ ⊥ (ABCD) => MQ ∈ α

Vậy α là mặt phẳng (OMQ).

Xác định thiết diện: Kéo dài QO cắt BC tại P là trung điểm của BC, ta có

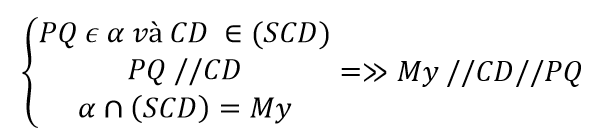bởi ∆AFC là tam giác đều.

Và My cắt SC tại N là trung điểm của SC.

Vậy mặt phẳng α cắt hình chóp S.ABCD theo thiết diện là hình thang vuông MNPQ.

Tính diện tích thiết diện: Ta có: S_MNPQ = 1/2(MN + PQ).MQ trong đó PQ = a và MN = 1/2CD = a/2 vì MN là đường trung bình của ΔSCD,

MQ = 1/2 SA = a/2, vì MQ là đường trung bình của ΔSAD,

=> S_MNPQ = 1/2(a + a/2).a/2 = 3a²/8

bởi ∆AFC là tam giác đều.

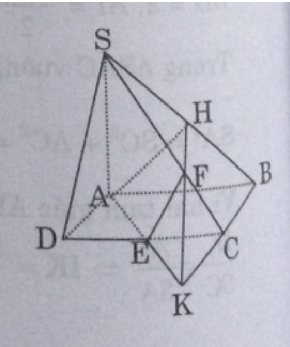
b. Ta lần lượt thực hiện:

Xác định mặt phẳng β: Trong (SAD) hạ AH ⊥ SB và H là trung điểm của AB, ta có:

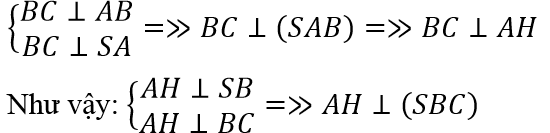bởi ∆AFC là tam giác đều.

=> AH ∈ β

Vậy β là mặt phẳng (AHE).

Xác định thiết diện: Kéo dài AE cắt BC tại K, nối HK cắt SC tại F.

Vậy mặt phẳng β cắt hình chóp S.ABCD theo thiết diện là tứ giác AEFH.

Tính diện tích thiết diện: Ta có:

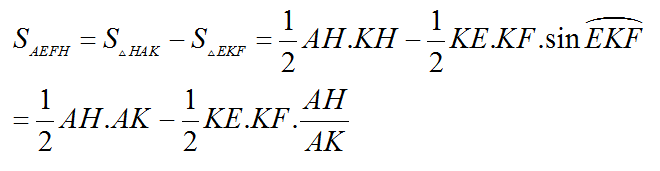bởi ∆AFC là tam giác đều.

Trong ΔSAB, ta có: AH = 1/2 SB = a√2/2

Trong ΔADE, ta có: AE = a√5/2

Trong ΔKAB, ta có:

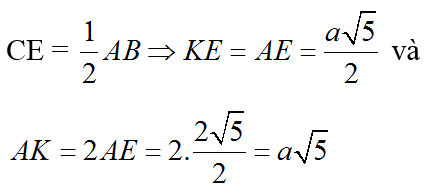bởi ∆AFC là tam giác đều.

Trong ΔHAK vuông tại H, ta có:

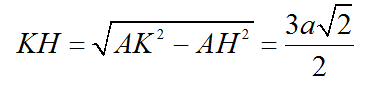bởi ∆AFC là tam giác đều.

Trong ΔSBK, ta có SC và SH là hai đường trung tuyến, do đó: KF = 3/2KH = a√2

Từ đó, ta được:

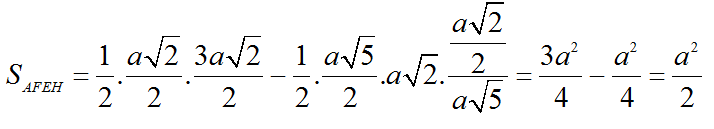bởi ∆AFC là tam giác đều.

---

---

---