Đáp án Đề thi Toán 11 Học kì 1 (Đề 8)

---

---

Đáp án Đề thi Toán 11 Học kì 1 (Đề 8)

Xem lại Đề kiểm tra Học kì 1 11 (Đề 8)

Phần trắc nghiệm

Câu 1: Đáp án D

Lời giải:

Ta biết rằng phép tịnh tiến theo vectơ v→ biến điểm M(x;y) thành điểm M’(x’;y’) với:

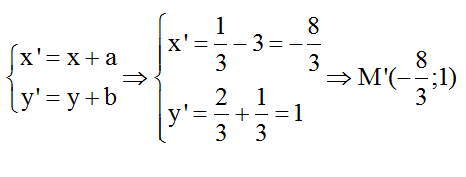
Câu 2: Đáp án B

Lời giải:

Để phép tịnh tiến theo vectơ v biến (d) thành chính nó thì vectơ v→ phải có giá song song với đường thẳng (d).

Nhận xét rằng đường thẳng (d) có vectơ chỉ phương a→ (-1;2)// (1/2;-1)

Do đó, chúng ta chọn đáp án B.

Câu 3: Đáp án D

Lời giải:

Mỗi điểm M’(x;y) ∈ (d') là ảnh của 1 điểm M(x_o;y_o) ∈ (d) qua phép đối xứng qua tâm O, ta có:

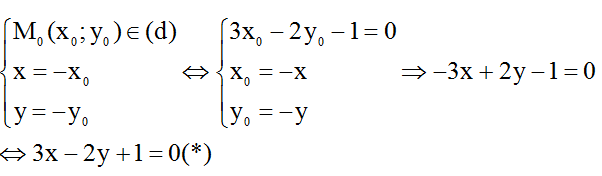
Phương trình (*) chính là phương trình của (d’).

Câu 4: Đáp án A

Lời giải:

Điều kiện: cos2x ≠ 0 ⇔ 2x ≠ π/2 + kπ ⇔ x ≠ π/4 + kπ/2 , k ∈ Z

Biến đổi phương trình về dạng:

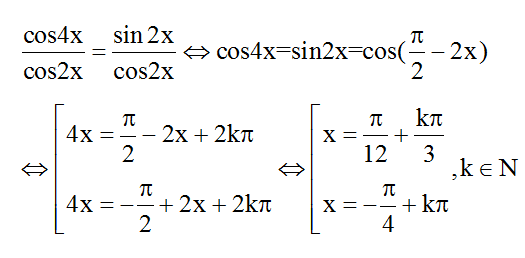
Khi đó, với x ∈ (0; π/2) ta được:

0 < x < π/2 ⇔ 0 < π/12 + kπ/3 < π/2 ⇔ -1/4 ≤ k ≤ 5/4 ⇔ k = 0 hoặc k = 1

Do vậy, trong (0; π/2) phương trình có 2 nghiệm là x= π/12 và x = 5π/12

Câu 5: Đáp án D

Lời giải:

Không gian mẫu là Ω có số phần tử là: 6.6=36

Gọi A là biến cố “hai con súc sắc đều xuất hiện mặt chẵn”, ta có: |A|=3.3=9 phần tử. Từ đó, suy ra: P(A)= 9/36 =1/4

Câu 6: Đáp án A

Lời giải:

Từ giả thiết, ta có:

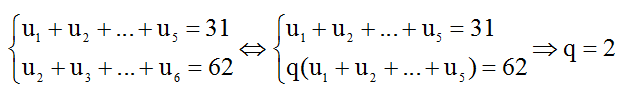
Mặt khác, ta cũng có:

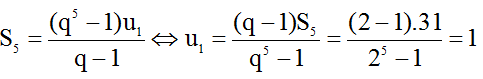
Vậy, ta được u₁=1 và q=2.

Phần tự luận

Bài 1:

Lời giải:

Sử dụng các phương pháp hình học, ta có:

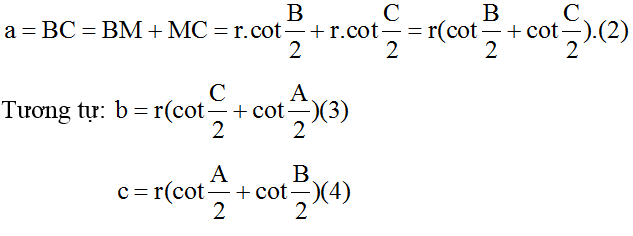
Thay (2), (3), (4) vào VT của (1) ta được điều cần chứng minh.

Bài 2:

Lời giải:

|m| > 1/8

Bài 3:

Lời giải:

Đặt E={1,2,3,4,5}. Một số 5 chữ số được ký hiệu: 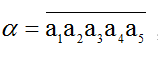, với a_i ∈ E .

Ta có:

Vì α nhỏ hơn 40000 nên a1 ∈ {1,2,3} => Có 3 cách chọn.

a₂, a₃, a₄,a₅ là 1 bộ phân biệt thứ tự được chọn từ E\{a1} do đó nó là 1hoán vị của 4 phần tử => Có P₄ cách chọn.

Vậy số các sô gồm 5 chữ số phân biệt nhỏ hơn 40000, hình thành từ tập E bằng: 3.P₄=72 số.

Bài 4:

Lời giải:

Ta có u₁=5; u₂= 5/3 ; u₃= 5/3²

Từ đó, bằng phương pháp quy nạp ta chứng minh được rằng u_n = 5/(3^n-1)

Bài 5:

Lời giải:

Không mất tính tổng quát ta giả sử ΔABC có đáy BC=a cố định và độ dài đường cao AH=h.

Từ đó suy ra đỉnh A chạy trên đường thẳng (d) song song và cách BC một khoảng bằng h.

Ta có: S_ΔABC = 1/2ah ⇔ r = ah/2p

Vậy r nhỏ nhất ⇔ có chu vi nhỏ nhất ⇔ AB+AC nhỏ nhất

⇔ A,B,C1 thẳng hàng, với C1 là điểm đối xứng với C qua (d).

---

---

---