Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Siêu sale sách Toán - Văn - Anh Vietjack 25-12 trên Shopee mall

Với tóm tắt lý thuyết Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Quảng cáo

Lý thuyết Đa giác đều. Hình đa giác đều trong thực tiễn

1. Đa giác. Đa giác lồi

1.1. Đa giác

Đa giác A₁A₂...A_n (n ≥ 3, n ∈ ℕ) là một hình gồm n đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ sao cho mỗi điểm A₁, A₂, ..., A_n là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác A₁A₂...A_n, các điểm A₁, A₂, ..., A_n là các đỉnh, các đoạn thẳng A₁A₂, A₂A₃, ..., A_{n – 1}A_n, A_nA₁ là các cạnh.

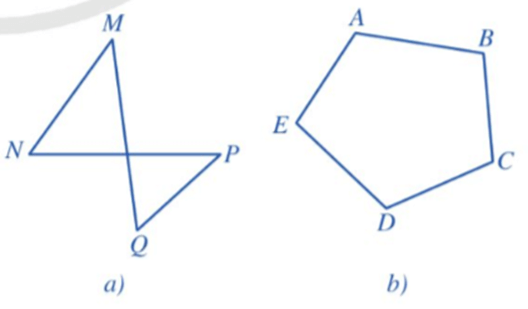
Ví dụ 1. Tứ giác MNPQ ở Hình a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM.Ngũ giác ABCDE ở Hình b gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Quan sát tứ giác MNPQ và ngũ giác ABCDE, ta nhận thấy:

– Mỗi đỉnh là điểm chung của đúng hai cạnh.

Quảng cáo

– Không có hai cạnh nào nằm trên cùng một đường thẳng.

Ta nói tứ giác MNPQ và ngũ giác ABCDE là những đa giác.

1.2. Đa giác lồi

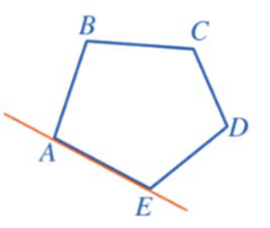
– Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Với ngũ giác lồi ABCDE ở hình vẽ trên, các góc ABC, BCD, CDE, DEA, EAB gọi là các góc của đa giác.

– Trong trường hợp tổng quát, đa giác lồi có n cạnh (n ≥ 3, n ∈ ℕ) cũng là đa giác lồi có n góc. Khi n lần lượt bằng 3; 4; 5; 6; ... ta có tam giác, tứ giác lồi, ngũ giác lồi, lục giác lồi, ...

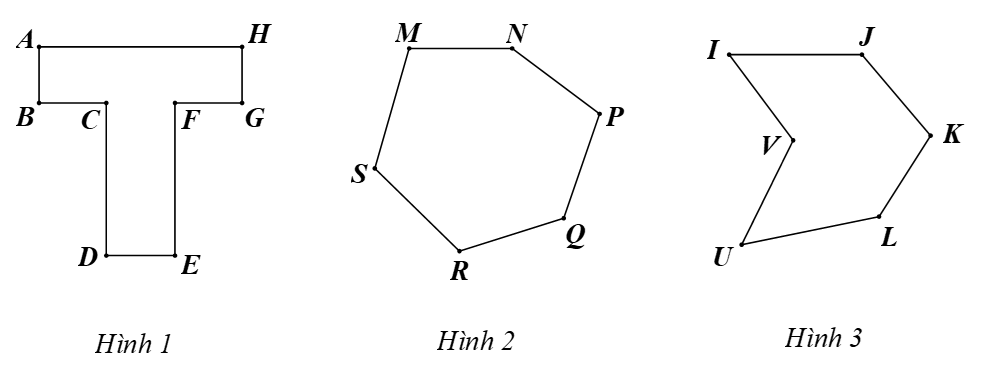
Ví dụ2. Quan sát các đa giác ở hình dưới đây và cho biết đã giác nào là đa giác lồi. Nêu tên các cạnh, các đỉnh, các góc của đa giác lồi đó.

Quảng cáo

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Hướng dẫn giải

– Ở Hình 1, do đa giác ABCDEFGH không nằm về một phía của đường thẳng chứa cạnh BC (hoặc CD, EF, FG) nên đa giác ABCDEFGH không phải là đa giác lồi.

– Ở Hình 2, do đa giác MNPQRS luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó nên đa giác MNPQRS là đa giác lồi.

Đa giác lồi MNPQRS có:

⦁ các cạnh là: MN, NP, PQ, QR, RS, SM;

⦁ có các đỉnh là: M, N, P, Q, R, S;

⦁ có các góc là: $\hat{M N P}, \hat{N P Q}, \hat{P Q R}, \hat{Q R S}, \hat{R S M}, \hat{S M N} .$

– Ở Hình 3, do đa giác IJKLUV không nằm về một phía của đường thẳng chứa cạnh UV (hoặc VI) nên đa giác IJKLUV không phải là đa giác lồi.

Quảng cáo

Quy ước:Từ nay về sau, khi nói về đa giác mà không chú thích gì thêm thì ta hiểu đó là đa giác lồi.

2. Đa giác đều

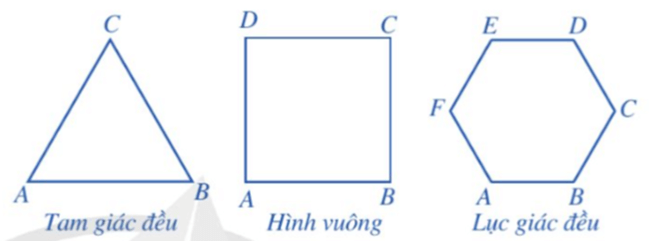
– Định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Chẳng hạn, tam giác đều, hình vuông, lục giác đều là các đa giác đều vì mỗi đa giác đó có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

– Đối với mỗi đa giác đều, có đúng một điểm O cách đều tất cả các đỉnh của đa giác đó. Điểm O đó được gọi là tâm của đa giác đều.

– Phần mặt phẳng giới hạn bởi đa giác đều được gọi là hình đa giác đều. Vì mỗi hình đa giác đều cũng là một phần của mặt phẳng nên hình đa giác đều còn gọi là hình phẳng đều.

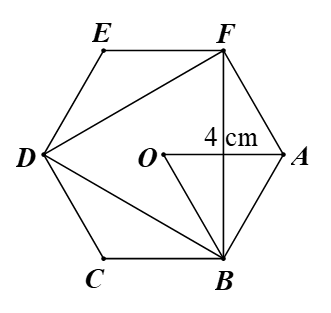
Ví dụ3. Cho lục giác đều ABCDEF tâm O, biết OA = 4 cm.

a) Tính số đo mỗi góc của lục giác đều ABCDEF.

b) Tính số đo mỗi cạnh của lục giác đều ABCDEF.

Hướng dẫn giải

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

a) Tổng 6 góc của lục giác đều ABCDEF bằng tổng các góc trong haitứ giác ABCD và ABEF.

Suy ra tổng 6 góc của lục giác đều ABCDEF bằng 2.360° = 720°.

Do tất cả các góc của lục giác đều bằng nhau nên số đo mỗi góc của lục giác đều bằng $\frac{720 °}{6} = 120 ° .$

Vậy số đo mỗi góc của lục giác đều ABCDEF đều bằng nhau và bằng 120°.

b) Ta có AF = AB (vì ABCDEF là lục giác đều) và OB = OF (vì O là tâm của lục giác đều ABCDEF).

Suy ra AO là đường trung trực của đoạn BF.

Vì AF = AB (chứng minh trên) nên tam giác ABF cân tại A.Do đó AO vừa là đường trung trực, vừa là đường phân giác của tam giác ABF.

Vì vậy $\hat{O A B} = \frac{\hat{B A F}}{2} = \frac{120 °}{2} = 60 ° .$

Ta có OB = OA = 4 cm (vì O là tâm của lục giác đều ABCDEF).

Suy ra tam giác OAB cân tại O, mà $\hat{O A B} = 60 °$ (chứng minh trên).

Do đó tam giác OAB đều, suy ra AB = OB = OA = 4 cm.

Vì vậy BC = CD = DE = EF = FA = AB = 4 cm (vì ABCDEF là lục giác đều).

Vậy số đo mỗi cạnh của lục giác đều ABCDEF đều bằng nhau và bằng 4 cm.

3. Hình đa giác đều trong thực tiễn

Trong thế giới tự nhiên, xuất hiện nhiều vật thể có hình ảnh liên quan đến hình đa giác đều. Dưới đây chúng ta sẽ tìm hiểu những vật thể có hình ảnh liên quan đến hình đa giác đều trong thế giới tự nhiên, trong nghệ thuật, kiến trúc và thiết kế, công nghệ.

3.1. Hình đa giác đều trong thế giới tự nhiên

Trong tự nhiên, vật thể có hình ảnh liên quan đến hình đa giác đều rất đa dạng, phong phú, chẳng hạn: bông hoa (hình a), con sao biển (hình b) có hình ảnh liên quan đến ngũ giác đều; tổ ong (Hình c) có hình ảnh liên quan đến lục giác đều; ...

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

3.2. Hình đa giác đều trong nghệ thuật, kiến trúc

Ngay từ xa xưa, con người trong quá trình chinh phục thế giới tự nhiên luôn khao khát tạo dựng được những công trình hài hòa và bền vững. Để làm được điều đó, họ đã nghiên cứu, phân tích cấu trúc của những hình khối cân đối nhất.

Một trong các nguyên tắc quan trọng nhất với nghệ thuật, hay kiến trúc là nguyên tắc cân bằng. Theo đó, các thiết kế về kiến trúc, đồ họa hay một tác phẩm nghệ thuật cần thực hiện tốt về cân bằng. Vì thế, bố cục kiểu đối xứng, cân bằng thường được sử dụng trong các tác phẩm nghệ thuật hay kiến trúc. Chẳng hạn, các vật thể có dạng như ở hình d, e, g được trang trí bởi hình tam giác đều, hình tứ giác đều, lục giác đều.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Trong thiết kế hay kiến trúc ta cũng thấy hình phẳng đều hiển hiện rất đa dạng, phong phú, chẳng hạn: Palmanova là một thị trấn thuộc Italia, được UNESCO công nhận là một di sản thế giới, điểm độc đáo nhất ở đây chính là kiến trúc của thị trấn gợi nên hình ảnh đa giác đều 18 cạnh (hình h). Toàn bộ thị trấn như một tổ hợp các pháo đài có kiến trúc cổ kính ở bên trong kết hợp với tổng thể tạo nên vẻ đẹp kì diệu.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Trong thiết kế, công nghệ, chúng ta cũng dễ dàng nhận ra các vật thể mà cấu trúc của chúng có dạng hình phẳng đều. Các công trình hay máy móc muốn tồn tại, ổn định, bền vững và có được vẻ đẹp thì phải chú trọng đến tính cân xứng, đều đặn. Theo đó, hình phẳng đều thường được sử dụng, chẳng hạn: các viên gạch lát nền (Hình i) có dạng hình vuông; bề mặt của ốc và đai ốc (Hình k) có dạng lục giác đều; chiếc đĩa (Hình m) có dạng hình đa giác đều tám cạnh; ...

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Bài tập Đa giác đều. Hình đa giác đều trong thực tiễn

Bài 1. Đa giác GHIJKLM là một hình gồm bao nhiêu đoạn thẳng?

A. 5;

B. 8;

C. 6;

D. 7.

Hướng dẫn giải

Đáp án đúng là: D

Đa giác GHIJKLM là một hình gồm 7 đoạn thẳng GH, HI, IJ, JK, KL, LM, MG.

Vậy ta chọn phương án D.

Bài 2. Phát biểu nào sau đây đúng nhất?

A. Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó;

B. Số cạnh và số góc của đa giác lồi luôn bằng nhau;

C. Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau;

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

Các phương án A, B, C đều đúng.Vậy ta chọn phương án D.

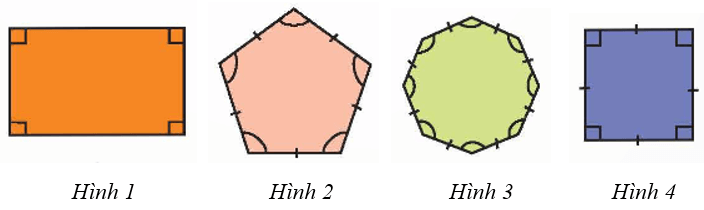
Bài 3. Trong các hình sau, hình nào không phải là đa giác đều?

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: A

Hình 1 là hình chữ nhật có chiều dài luôn lớn hơn chiều rộng.Do đó Hình 1 không phải là đa giác đều.

Hình 2 là ngũ giác đều.

Hình 3 là bát giác đều.

Hình 4 là tứ giác đều (hình vuông).

Vậy ta chọn phương án A.

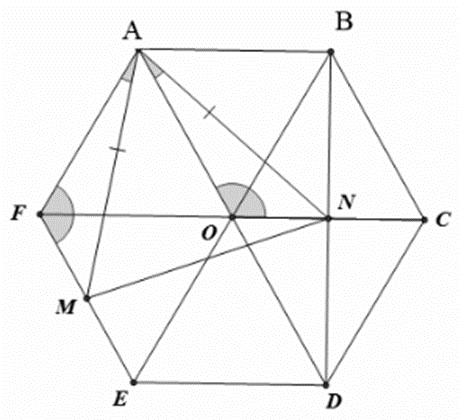
Bài 4. Cho lục giác đều ABCDEF tâm O. Gọi M, N lần lượt là trung điểm của EF, BD. Chứng minh rằng:

a) N là trung điểm OC.

b) ∆AFM = ∆AON.

c) Tam giác AMN đều.

Hướng dẫn giải

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

a) Tổng 6 góc của lục giác đều ABCDEF bằng tổng các góc trong hai tứ giác ABCD và AFED.

Suy ra tổng 6 góc của lục giác đều ABCDEF bằng 2.360° = 720°.

Do tất cả các góc của lục giác đều bằng nhau nên số đo mỗi góc của lục giác đều bằng $\frac{720 °}{6} = 120 °$ hay $\hat{A F M} = \hat{B C D} = 120 ° .$

Vì CB = CD (chứng minh trên) nên tam giác BCD cân tại C.Do đó CO vừa là đường trung tuyến, vừa là đường phân giác của tam giác BCD.

Vì vậy $\hat{O C B} = \frac{\hat{B C D}}{2} = \frac{120 °}{2} = 60 ° .$

Ta có OB = OC (vì O là tâm của lục giác đều ABCDEF).

Suy ra tam giác OBC cân tại O.

Mà $\hat{O C B} = 60 °$ (chứng minh trên).Do đó tam giác OBC đều.

Chứng minh tương tự cho các tam giác OCD, OAB, OAF, ODE, OEF, ta được ∆OCD, ∆OAB, ∆OAF, ∆ODE, ∆OEF là các tam giác đều.

Ta có tam giác OBC đều nên OB = BC = OC, mà OB = OC = OD và BC = CD nên OB = BC = CD = OD. Suy ra tứ giác OBCD là hình thoi.

Do đó hai đường chéo OC và BD vuông góc với nhau tại trung điểm N của mỗi đường.

Vậy N là trung điểm OC.

b) Ta có $\hat{A O B} = \hat{B O C} = 60 °$ (vì các tam giác OAB, OBC đều).

Suy ra $\hat{A O C} = \hat{A O B} + \hat{B O C} = 60 ° + 60 ° = 120 ° .$

Ta có EF = OC (cùng bằng OF) và M, N lần lượt là trung điểm EF, OC nên FM = ON.

Xét ∆AFM và ∆AON, có:

$\hat{A F M} = \hat{A O N} = 120 °;$

AF = AO (tam giác OAF đều);

FM = ON (chứng minh trên).

Do đó ∆AFM = ∆AON (c.g.c).

c) Từ kết quả câu b), ta được AM = AN và $\hat{F A M} = \hat{O A N} .$

Suy ra ∆AMN cân tại A.

Ta có $\hat{F A O} = 60 °$ (do ∆OAF đều).

Suy ra $\hat{F A M} + \hat{M A O} = 60 °$ nên $\hat{O A N} + \hat{M A O} = 60 °$ hay $\hat{M A N} = 60 ° .$

Xét ∆AMN cân tại A có $\hat{M A N} = 60 °$ nên ∆AMN đều.

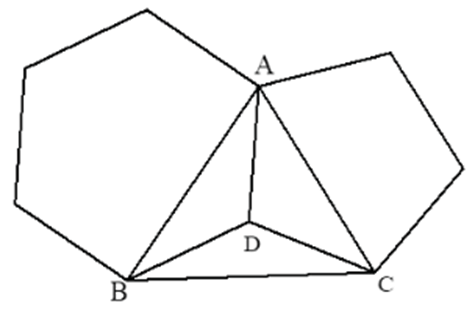
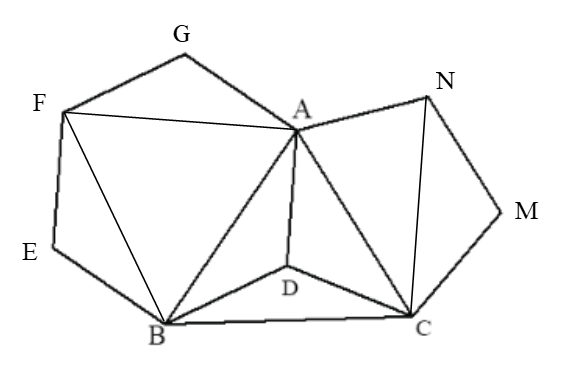
Bài 5. Cho một lục giác đều và một ngũ giác đều chung cạnh AD (như hình vẽ). Tính số đo các góc của tam giác ABC.

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Hướng dẫn giải

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Gọi ADBEFG là lục giác đều và ADCMN là ngũ giác đều.

Vì lục giác đều ADBEFG và ngũ giác đều ADCMN có chung cạnh AD nên tất cả các cạnh của lục giác đều ADBEFG và ngũ giác đều ADCMN đều bằng nhau.

– Tổng 6 góc của lục giác đều ADBEFG bằng tổng các góc trong bốn tam giác ABD, BEF, AFG, ABF.

Suy ra tổng 6 góc của lục giác đều ADBEFG bằng 4.180° = 720°.

Do tất cả các góc của lục giác đều bằng nhau nên số đo mỗi góc của lục giác đều bằng $\frac{720 °}{6} = 120 °$ hay $\hat{A D B} = 120 ° .$

Vì AD = BD (ADBEFG là lục giác đều) nên tam giác ABD cân tại D.

Suy ra $\hat{B A D} = \hat{A B D} .$

Tam giác ABD, có: $\hat{A D B} + \hat{B A D} + \hat{A B D} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $2 \hat{A B D} = 180 ° - \hat{A D B} = 180 ° - 120 ° = 60 ° .$

Do đó $\hat{B A D} = \hat{A B D} = 30 ° .$

–Tổng 5 góc của ngũ giác đều ADCMN bằng tổng các góc trong ba tam giác ACD, ACN, CMN.

Suy ra tổng 5 góc của ngũ giác đều ADCMN bằng 3.180° = 540°.

Do tất cả các góc của ngũ giác đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng $\frac{540 °}{5} = 108 °$ hay $\hat{A D C} = 108 ° .$

Vì AD = CD (ADCMN là ngũ giác đều) nên tam giác ACD cân tại D.

Suy ra $\hat{D A C} = \hat{D C A} .$

Tam giác ACD, có: $\hat{A D C} + \hat{D A C} + \hat{D C A} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $2 \hat{D C A} = 180 ° - \hat{A D C} = 180 ° - 108 ° = 72 ° .$

Do đó $\hat{D A C} = \hat{D C A} = 36 ° .$

– Ta có $\hat{A D B} + \hat{A D C} + \hat{B D C} = 360 ° .$

Suy ra $\hat{B D C} = 360 ° - (\hat{A D B} + \hat{A D C}) = 360 ° - (120 ° + 108 °) = 132 ° .$

Ta có BD = CD (= AD) nên tam giác BCD cân tại D.Do đó $\hat{D B C} = \hat{D C B} .$

Tam giác BCD, có: $\hat{B D C} + \hat{D B C} + \hat{D C B} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $2 \hat{D C B} = 180 ° - \hat{B D C} = 180 ° - 132 ° = 48 ° .$

Do đó $\hat{D B C} = \hat{D C B} = 24 ° .$

– Tam giác ABC, có:

⦁ $\hat{B A C} = \hat{B A D} + \hat{D A C} = 30 ° + 36 ° = 66 °;$

⦁ $\hat{A B C} = \hat{A B D} + \hat{D B C} = 30 ° + 24 ° = 54 °;$

⦁ $\hat{A C B} = \hat{A C D} + \hat{D C B} = 36 ° + 24 ° = 60 ° .$

Vậy $\hat{B A C} = 66 °; \hat{A B C} = 54 °; \hat{A C B} = 60 ° .$

Bài 6. Tìm một số hình ảnh trong tự nhiên, trong nghệ thuật, trang trí, thiết kế, công nghệ,... những vật thể mà cấu trúc của nó có dạng hình đa giác đều.

Hướng dẫn giải

Trong tự nhiên, trong nghệ thuật, trang trí, thiết kế, công nghệ,... có rất nhiều vật thể mà cấu trúc của nó có dạng hình đa giác đều.

⦁ Trong tự nhiên:

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

⦁ Trong nghệ thuật, trang trí:

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

⦁ Trong thiết kế, công nghệ:

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

⦁ Các vật dụng trong đời sống:

Đa giác đều. Hình đa giác đều trong thực tiễn (Lý thuyết Toán lớp 9) | Cánh diều

Học tốt Đa giác đều. Hình đa giác đều trong thực tiễn

Các bài học để học tốt Đa giác đều. Hình đa giác đều trong thực tiễn Toán lớp 9 hay khác:

Giải sgk Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn

Xem thêm tóm tắt lý thuyết Toán lớp 9 Chân trời sáng tạo hay khác:

Xem thêm các tài liệu học tốt lớp 9 hay khác:

Tủ sách VIETJACK luyện thi vào 10 cho 2k10 (2025):

Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

ĐỀ THI, GIÁO ÁN, SÁCH ĐỀ THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9

Bộ giáo án, bài giảng powerpoint, đề thi dành cho giáo viên và sách dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi vào 10 Toán Văn Anh của Hà Nội, Tp.Hồ Chí Minh... có lời giải

4.5 (243)

799,000đ

199,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.