Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố lớp 9 (Lý thuyết Toán 9 Cánh diều)
Với tóm tắt lý thuyết Toán 9 Bài 4: Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.
Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố lớp 9 (Lý thuyết Toán 9 Cánh diều)
Bài giảng: Bài 4: Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố - Cô Vương Hạnh (Giáo viên VietJack)
Lý thuyết Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố
1. Phép thử ngẫu nhiên và không gian mẫu
– Có những phép thử mà tập hợp Ω gồm các kết quả có thể xảy ra của phép thử đó hoàn toàn xác định. Tuy nhiên, các kết quả xảy ra có tính ngẫu nhiên, ta không thể đoán trước được. Những phép thử như thế gọi là phép thử ngẫu nhiên (gọi tắt là phép thử) và tập hợp W gọi là không gian mẫu của phép thử.
– Các kết quả có thể xảy ra của một phép thử có khả năng xuất hiện như nhau được gọi là đồng khả năng.
– Kết quả thuận lợi cho biến cố A là một kết quả có thể của phép thử làm cho biến cố A xảy ra
Ví dụ 1. Xét phép thử “Lấy ra lần lượt hai quả bóng và không trả lại quả bóng được lấy ra từ lần đầu tiên từ một hộp chứa ba quả bóng được đánh số 1; 2; 3”.
a) Nêu các kết quả có thể xảy ra đối với mặt xuất hiện của hai quả bóng.
b) Viết không gian mẫu của phép thử đó.
Hướng dẫn giải
Kết quả của phép thử là cặp số (a, b), trong đó a và b tương ứng là số xuất hiện trên quả bóng thứ nhất và thứ hai. Do không trả lại quả bóng được lấy ra từ lần đầu tiên nên a ≠ b.
a) Các kết quả có thể xảy ra đối với bóng xuất hiện của ba quả bóng là:
(1, 2); (1, 3); (2, 1); (2, 3); (3, 1); (3, 2).
b) Không gian mẫu của phép thử đó là:
= {(1, 2); (1, 3); (2, 1); (2, 3); (3, 1); (3, 2)}.
2. Xác suất của biến cố
– Giả thiết rằng các kết quả có thể xảy ra của một phép thử là đồng khả năng.
Khi đó, xác suất của biến cố A, kí hiệu là P(A), bằng tỉ số giữa số kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra:
– Để tính xác suất cho biến cố A, ta có thể thực hiện các bước sau:
Bước 1. Kiểm tra tính đồng khả năng đối với các kết quả có thể xảy ra của phép thử
Bước 2. Đếm số kết quả có thể xảy ra, tức là đếm số phần tử của không gian mẫu W
Bước 3. Đếm số kết quả thuận lợi cho biến cố A
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra.
Ví dụ 2.Có ba người A, B, C cùng đến phòng họp một lúc để phỏng vấn xin việc. Nhà tuyển dụng sẽ chọn lần lượt từng người trên để phỏng vấn theo thứ tự ngẫu nhiên.
a) Viết tập hợp W gồm các kết quả có thể xảy ra đối với từng người được phỏng vấn.
b) Tính xác suất của biến cố M: “Người C được phỏng vấn đầu tiên”.
c) Tính xác suất của biến cố N: “Người B được phỏng vấn trước người A”.
Hướng dẫn giải
Xét phép thử: “Chọn lần lượt từng người trong ba người A, B, C để phỏng vấn theo thứ tự ngẫu nhiên”.
Kết quả của phép thử là bộ chữ (x, y, z), trong đó x, y và z lần lượt là tên người được chọn vào phỏng vấn theo thứ tự thứ nhất, thứ hai và thứ ba.
Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.
a) Tập hợp gồm các kết quả có thể xảy ra đối với hai bông hoa được lấy ra là:
= {(A, B, C); (A, C, B); (B, A, C); (B, C, A); (C, A, B); (C, B, A)}.
Do đó tập hợp W có 6 phần tử.
b) Các trường hợp người C được phỏng vấn đầu tiên là: (C, A, B); (C, B, A)}.
Dó đó có 2 kết quả thuận lợi cho biến cố M: “Người C được phỏng vấn đầu tiên”.
Vậy xác suất của biến cố M là
c) Các trường hợp người B được phỏng vấn trước người A là: (B, A, C); (B, C, A); (C, B, A).
Dó đó có 3 kết quả thuận lợi cho biến cố N: “Người B được phỏng vấn trước người A”.
Vậy xác suất của biến cố N là
Ví dụ 3. Nam và Quân học lớp 9A và Trang, Hùng học lớp 9B. Xếp 4 bạn ngồi thành hàng ngang. Tính xác suất để các bạn cùng lớp không ngồi cạnh nhau.
Hướng dẫn giải
Kí hiệu bốn bạn Nam, Quân, Trang, Hùng lần lượt là N, Q, T, H.
Có 24 cách xếp 4 bạn ngồi thành hàng ngang là: (N, Q, T, H), (N, Q, H, T), (N, T, Q, H), (N, T, H, Q), (N, H, Q, T), (N, H, T, Q), (Q, N, T, H), (Q, N, H, T), (Q, T, N, H), (Q, T, H, N), (Q, H, N, T), (Q, H, T, N), (T, H, N, Q), (T, H, Q, N), (T, N, Q, H), (T, N, H, Q), (T, Q, N, H), (T, Q, H, N), (H, T, Q, N), (H, T, N, Q), (H, Q, T, N), (H, Q, N, T), (H, N, T, Q), (H, N, Q, T).
Không gian mẫu có 24 phần tử.
Có 8 cách sắp xếp để 2 bạn cùng lớp không ngồi cạnh nhau là: (N, T, Q, H), (N, H, Q, T), (Q, T, N, H), (Q, H, N, T), (T, N, H, Q), (T, Q, H, N), (H, N, T, Q), (H, Q, T, N).
Vậy xác suất để các bạn cùng lớp không ngồi cạnh nhau là:
Bài tập Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố
Bài 1. Xét phép thử “Gieo một đồng xu hai lần liên tiếp và quan sát mặt xuất hiện trên đồng xu”. Không gian mẫu của phép thử là
A. = {S; SN; N; SS}.
B. = {NS; SN; NN; SS}.
C. = {NN; SS}.
D. = {NS; NN; SS}.
Hướng dẫn giải
Đáp án đúng là: B
Không gian mẫu của phép thử đó là = {NS; SN; NN; SS}.
Bài 2. Cho tập hợp A = {0; 1; 5; 6}.Mai dùng 2 chữ số khác nhau từ tập hợp A để tạo thành số có hai chữ số. Số kết quả thuận lợi của biến cố: “Số tạo thành chia hết cho 5” là
A. 2;
B. 3;
C. 5;
D. 6.
Hướng dẫn giải
Đáp án đúng là: C
Có 5 kết quả thuận lợi của biến cố: “Số tạo thành chia hết cho 5” là: {10; 50; 60; 15; 65}.
Vậy ta chọn phương án C.
Bài 3. Gieo một con xúc xắc đồng chất và cân đối một lần. Xác suất của biến cố A: “Xúc xắc xuất hiện mặt có số chấm là số nguyên tố” là
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của con xúc xắc là:
W = {1; 2; 3; 4; 5; 6}.
Do đó tập hợp có 6 phần tử.
Trường hợp xuất hiện mặt có số chấm là số nguyên tố là: 2 chấm; 3 chấm; 5 chấm.
Dó đó có 3 kết quả thuận lợi cho biến cố A: “Xúc xắc xuất hiện mặt có số chấm là số nguyên tố”.
Vậy xác suất của biến cố A là
Bài 4.Xét phép thử: “Gieo ngẫu nhiên hai con súc sắc cân đối và đồng chất”. Tính xác suất của các biến cố sau:
a) A: “Tổng số chấm trên hai mặt bằng 11”;
b) B: “Kết quả sau hai lần gieo là như nhau”;
c) C: “Tích số chấm trên hai mặt lớn hơn 12”.
Hướng dẫn giải
Kết quả của phép thử là cặp số (a, b), trong đó a và b tương ứng là số chấm lần lượt xuất hiện trên con xúc xắc thứ nhất và thứ hai.
Không gian mẫu của phép thử là:
Ω={(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6); (3, 1); (3, 2); (3, 3); (3, 4);(3, 5);(3, 6);(4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)}.
Số phần tử không gian mẫu: 36.
a) Các kết quả có tổng số chấm trên hai mặt của hai con xúc xắc bằng 11 là (5, 6) và (6, 5).
Do đó biến cố A có 2 kết quả thuận lợi.
Vậy
b) Các kết quả có số chấm trên hai mặt của hai con xúc xắc bằng nhau là: (1, 1); (2, 2); (3, 3); (4, 4); (5, 5); (6, 6).
Do đó biến cố B có 6 kết quả thuận lợi.
Suy ra
c) Các kết quả có tích số chấm trên hai mặt của hai con xúc xắc lớn hơn 10 là: (3, 5); (3, 6); (4, 4); (4, 5); (4, 6); (5, 3); (5, 4); (5, 5); (5, 6); (6, 3); (6, 4); (6, 5); (6, 6).
Do đó biến cố C có 6 kết quả thuận lợi.
Suy ra
Bài 5. Có năm đoạn thẳng có độ dài lần lượt là 2 cm, 4 cm, 6 cm, 8 cm và 10 cm. Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng trên. Tính xác suất của biến cố A: “Ba đoạn thẳng được lấy ra lập thành ba cạnh của một tam giác”.
Hướng dẫn giải:
Xét phép thử “Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng”.
Ta thấy, các kết quả xảy ra của phép thử đó là đồng khả năng.
Kết quả xảy ra của phép thử là một bộ ba (a cm, b cm, c cm), trong đó a cm, b cm và c cm tương ứng là độ dài của ba đoạn thẳng được lấy ra. Do ba đoạn thẳng được lấy ra cùng một lúc nên a, b và c đôi một khác nhau.
Tập hợp các kết quả của phép thử là:
Ω = {(2 cm, 4 cm, 6 cm); (2 cm, 4 cm, 8 cm); (2 cm, 4 cm, 10 cm); (2 cm, 6 cm, 8 cm); (2 cm, 6 cm, 10 cm); (2 cm, 8 cm, 10 cm); (4 cm, 6 cm, 8 cm); (4 cm, 6 cm, 10 cm); (4 cm, 8 cm, 10 cm); (6 cm, 8 cm, 10 cm)}.
Tập hợp Ω có 10 phần tử.
Ta có: 8 < 4 + 6; 10 < 4 + 8; 10 < 6 + 8 nên ba bộ ba các đoạn thẳng lập thành ba cạnh của một tam giác là: (4 cm, 6 cm, 8 cm); (4 cm, 8 cm, 10 cm); (6 cm, 8 cm, 10 cm).
Do đó có 3 kết quả thuận lợi cho biến cố A.
Vậy xác suất của biến cố A là:
Học tốt Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố
Các bài học để học tốt Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố Toán lớp 9 hay khác:
Xem thêm tóm tắt lý thuyết Toán lớp 9 Cánh diều hay khác:
Xem thêm các tài liệu học tốt lớp 9 hay khác:
- Giải sgk Toán 9 Cánh diều
- Giải SBT Toán 9 Cánh diều
- Giải lớp 9 Cánh diều (các môn học)
- Giải lớp 9 Kết nối tri thức (các môn học)
- Giải lớp 9 Chân trời sáng tạo (các môn học)
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải sgk Toán 9 Tập 1 & Tập 2 của chúng tôi được biên soạn bám sát nội dung sgk Toán 9 Cánh diều (NXB Đại học Sư phạm).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều

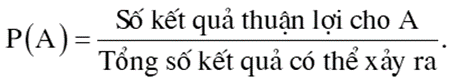



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

