Tổng hợp lý thuyết Toán 9 Chương 7 Cánh diều
Tổng hợp lý thuyết Toán 9 Chương 7: Hàm số y = ax2 (a ≠ 0). Phương trình bậc hai một ẩn sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 7.
Tổng hợp lý thuyết Toán 9 Chương 7 Cánh diều
Tổng hợp lý thuyết Toán 9 Chương 7
1. Hàm số y = ax2 (a ≠ 0)
Hàm số y = ax2 (a ≠ 0) xác định với mọi giá trị x thuộc ℝ.
2. Đồ thị của hàm số y = ax2 (a ≠ 0)
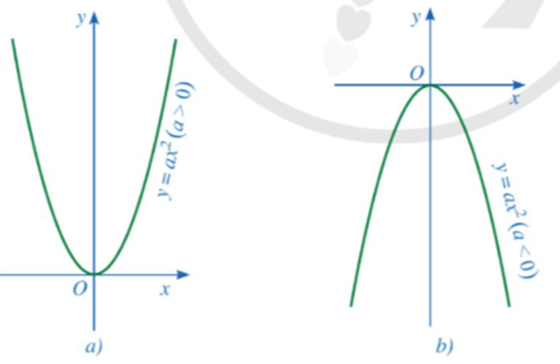
– Trong trường hợp tổng quát, đồ thị của hàm số y = ax2 (a ≠ 0) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc tọa độ và có dạng như sau:
– Nếu a > 0 thì đồ thị đó nằm phía trên trục hoành (Hình a).
Ngược lại, nếu a < 0 thì đồ thị đó nằm phía dưới trục hoành (Hình b).
– Để vẽ đồ thị của hàm số y = ax2 (a ≠ 0), ta có thể thực hiện các bước sau:
Bước 1. Lập bảng giá trị để tìm giá trị của y tương ứng với một số giá trị cụ thể của x
Bước 2. Căn cứ vào bảng giá trị, vẽ một số điểm cụ thể thuộc đồ thị của hàm số đó
Bước 3. Vẽ parabol đi qua gốc tọa độ và các điểm đã xác định ở Bước 2, ta nhận được đồ thị của hàm số y = ax2 (a ≠ 0).
Tính chất: Đồ thị của hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng.
3. Định nghĩa phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng ax2 + bx + c = 0, trong đó x là ẩn; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.
4. Giải phương trình bậc hai một ẩn
– Cho m, n là hai số thực. Ta có thể giải phương trình (x – n)2 = m như sau:
⦁ Khi m > 0, ta có: (x – n)2 = m
hoặc
hoặc
Như vậy, phương trình có hai nghiệm là và
⦁ Khi m = 0, phương trình có nghiệm x1 = x2 = n (nghiệm kép).
⦁ Khi m < 0, phương trình vô nghiệm.
– Ta có thể giải phương trình ax2 + bx + c = 0 (a ≠ 0) theo các bước sau:
Bước 1. Chia hai vế của phương trình cho a, ta được phương trình:
(1)
Bước 2. Viết lại số hạng và thêm số hạng vào hai vế của phương trình (1) rồi biến đổi để vế trái thành bình phương của một biểu thức:
Bước 3. Kí hiệu ∆ = b2 – 4ac và gọi nó là biệt thức của phương trình (∆ là một chữ cái Hy Lạp, đọc là “đenta”). Khi đó, phương trình (1) viết được về dạng:
(2)
Bước 4. Giải phương trình (2). Từ đó, kết luận nghiệm của phương trình đã cho.
– Tóm lại, ta có kết luận chung sau:
Xét phương trình ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac.
⦁ Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
⦁ Nếu ∆ = 0 thì phương trình có nghiệm kép
⦁ Nếu ∆ < 0 thì phương trình vô nghiệm.
Xét phương trình ax2 + bx + c = 0 (a ≠ 0) với b = 2b’ và ∆’ = b’2 – ac.
⦁ Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt
⦁ Nếu ∆’ = 0 thì phương trình có nghiệm kép
⦁ Nếu ∆’ < 0 thì phương trình vô nghiệm.
Công thức nghiệm vừa viết trên đây được gọi là công thức nghiệm thu gọn.
5. Ứng dụng của phương trình bậc hai một ẩn
– Để giải bài toán bằng cách lập phương trình bậc hai, ta có thể làm như sau:
Bước 1. Lập phương trình bậc hai
⦁ Chọn ẩn số và đặt điều kiện cho ẩn số
⦁ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
⦁ Lập phương trình bậc hai biểu thị mối quan hệ giữa các đại lượng
Bước 2. Giải phương trình bậc hai
Bước 3. Kết luận
⦁ Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn, nghiệm nào không thỏa mãn điều kiện của ẩn
⦁ Đưa ra câu trả lời cho bài toán.
6. Sử dụng máy tính cầm tay để tìm nghiệm của phương trình bậc hai một ẩn
Ta có thể tìm nghiệm (đúng hoặc gần đúng) của phương trình bậc hai một ẩn bằng cách sử dụng máy tính cầm tay. Mỗi loại máy tính khác nhau có thể có hệ thống phím, chức năng và cách sử dụng khác nhau. Tuy nhiên, chúng đều có quy tắc chung là phải mở chương trình giải phương trình bậc hai một ẩn rồi mới nhập dữ liệu. Chẳng hạn, ấn liên tiếp các phím
Ví dụ. Sử dụng máy tính cầm tay để tìm nghiệm của phương trình bậc hai một ẩn (làm tròn kết quả đến hàng phần mười):
Hướng dẫn giải
Sử dụng loại máy tính phù hợp, ấn liên tiếp các phím:
Ta thấy trên màn hình hiện ra (kết quả gần đúng): x1 = 0,7883402059.
Ấn tiếp phím 
Vậy nghiệm của phương trình đã cho là x1 ≈ 0,8 và x2 ≈ –0,9.
7. Định lí Viète
Định lí Viète chỉ ra mối liên hệ giữa tổng và tích của hai nghiệm với các hệ số của phương trình bậc hai một ẩn:
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì
Nhận xét:
⦁ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
⦁ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x1 = –1 và nghiệm còn lại là
8. Tìm hai số khi biết tổng và tích
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình
x2– Sx + P = 0.
Chú ý: Điều kiện để có hai số đó là S2 – 4P ≥ 0.
Bài tập ôn tập Chương 7
I. Bài tập trắc nghiệm
Bài 1. Điểm nào sau đây thuộc đồ thị hàm số y = 12x2?
A. M(1; –12);
B. N(–1; 6);
C. P(2; 48);
D. Q(–2; –4).
Hướng dẫn giải
Đáp án đúng là: C
Ta có: 12.12 = 12 ≠ –12 nên điểm M(1; –12) không thuộc đồ thị hàm số y = 12x2.
Thực hiện tương tự như vậy, ta được các điểm N(–1; 6), Q(–2; –4) không thuộc đồ thị hàm số y = 12x2 và điểm P(2; 48) thuộc đồ thị hàm số y = 12x2.
Vậy ta chọn phương án C.
Bài 2. Cho hàm số y = –5x2. Khi y = –20 thì
A. x = –1 hoặc x = 1;
B. x = 2 hoặc x = –2;
C. x = 2;
D. x = –2.
Hướng dẫn giải
Đáp án đúng là: B
Xét hàm số y = –5x2, với y = –20, ta có: –5x2 = –20.
Suy ra x2 = 4 = 22 = (–2)2.
Do đó x = 2 hoặc x = –2.
Vậy ta chọn phương án B.
Bài 3. Cho hàm số y = ax2 (a ≠ 0). Khẳng định nào sau đây đúng?
A. Đồ thị của hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ và có Ox là trục đối xứng;
B. Đồ thị của hàm số y = ax2 (a ≠ 0) là một đường thẳng đi qua gốc tọa độ và có Oy là trục đối xứng;
C. Nếu a > 0 thì đồ thị của hàm số đã cho nằm phía dưới trục Ox;
D. Nếu a < 0 thì đồ thị của hàm số đã cho nằm phía dưới trục Ox.
Hướng dẫn giải
Đáp án đúng là: D
Phương án A, B sai. Sửa lại: Đồ thị của hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ và có Oy là trục đối xứng.
Phương án C sai. Sửa lại: Nếu a > 0 thì đồ thị của hàm số đã cho nằm phía trên trục Ox.
Phương án D đúng.
Vậy ta chọn phương án D.
Bài 4. Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn?
A. t3 – 7t + 9 = 0;
B. –11x2 = 0;
C.
D. 0y2 + 2y = 0.
Hướng dẫn giải
Đáp án đúng là: B
Phương trình ở phương án A không là phương trình bậc hai vì có chứa t3.
Phương trình ở phương án B là phương trình bậc hai ẩn x và có a = –11; b = c = 0.
Phương trình ở phương án C không là phương trình bậc hai vì có chứa ẩn x dưới mẫu thức.
Phương trình ở phương án D không là phương trình bậc hai vì a = 0.
Bài 5. Phương trình (x + 3)2 = 25 có nghiệm là
A. x = 8;
B. x = –2;
C. x = 2 và x = –8;
D. x = –8.
Hướng dẫn giải
Đáp án đúng là: C
Ta có: (x + 3)2 = 25.
hoặc
x + 3 = 5 hoặc x + 3 = –5
x = 2 hoặc x = –8.
Vậy phương trình đã cho có hai nghiệm là x = 2 và x = –8.
Do đó ta chọn phương án C.
Bài 6. Để tìm nghiệm của phương trình bằng cách sử dụng máy tính cầm tay, ta ấn liên tiếp các phím
Hướng dẫn giải
Đáp án đúng là: A
Sử dụng loại máy tính phù hợp, ấn liên tiếp các phím:
Vậy ta chọn phương án A.
Bài 7. Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình x2 – 3x + 2 = 0. Khi đó giá trị của S và P là
A. S = –3 và P = 2;
B. S = 2 và P = 3;
C. S = 3 và P = –2;
D. S = 3 và P = 2.
Hướng dẫn giải
Đáp án đúng là: D
Phương trình đã cho có các hệ số a = 1; b = –3; c = 2.
Theo định lí Viète, ta có:
và
Vậy S = 3 và P = 2.
Do đó ta chọn phương án D.
Bài 8. Phương trình x2 + bx + c = 0 thỏa mãn b + c = –1 thì có hai nghiệm là
A. x1 = 1 và x2 = c;
B. x1 = –1 và x2 = –c;
C. x1 = 2 và x2 = b;
D. x1 = x2 = b.
Hướng dẫn giải
Đáp án đúng là: A
Xét phương trình x2 + bx + c = 0 có hệ số a = 1.
Ta thấy a + b + c = 1 + b + c = 1 + (–1) = 0.
Suy ra phương trình đã cho có hai nghiệm là x1 = 1 và
Vậy ta chọn phương án A.
Bài 9. Điều kiện tồn tại hai số có tổng bằng S và tích bằng P là
A. S2 – 4P ≥ 0;
B. S2 ≥ P;
C. S2 + 4P ≥ 0;
D. P2 + 4S ≥ 0.
Hướng dẫn giải
Đáp án đúng là: A
Điều kiện để có hai số có tổng bằng S và tích bằng P là S2 – 4P ≥ 0.
Vậy ta chọn phương án A.
II. Bài tập tự luận
Bài 1. Cho hàm số y = ax2 (a ≠ 0).
a) Tìm a, biết đồ thị của hàm số đã cho đi qua điểm G(1; –1).
b) Vẽ đồ thị của hàm số đã cho với a vừa tìm được.
c) Tìm các điểm thuộc đồ thị của hàm số đã cho có tung độ bằng –25. Từ đó nhận xét về tính đối xứng giữa các điểm đó.
Hướng dẫn giải
a) Vì G(1; –1) thuộc đồ thị hàm số đã cho nên ta có:
–1 = a.12, suy ra a = –1 (thỏa mãn).
Vậy a = –1.
b) Với a = –1, ta có hàm số y = –x2.
Ta có bảng giá trị của y tương ứng với giá trị của x như sau:

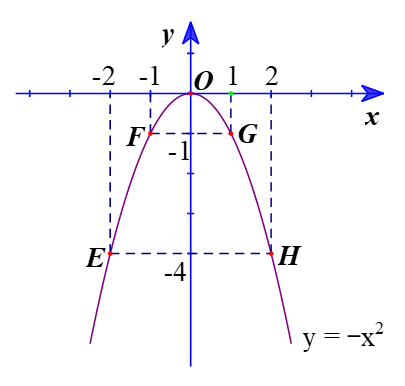
– Vẽ các điểm E(–2; –4), F(–1; –1), O(0; 0), G(1; –1), H(2; –4) thuộc đồ thị của hàm số y = –x2 trong mặt phẳng tọa độ Oxy.
– Vẽ đường parabol đi qua năm điểm E, F, O, G, H, ta nhận được đồ thị của hàm số y = –x2 như hình bên dưới:
c) Với y = –25, ta có –25 = –x2.
Suy ra x2 = 25 = 52 = (–5)2
Do đó x = 5 hoặc x = –5.
Vậy các điểm thuộc đồ thị của hàm số đã cho có tung độ bằng –25 là U(5; –25) và V(–5; –25).
Ta thấy hai điểm U và V có tung độ bằng nhau và có hoành độ đối nhau.
Vậy cặp điểm U và V đối xứng với nhau qua trục Oy.
Bài 2. Không cần giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức ∆ và xác định số nghiệm của mỗi phương trình sau:
a) 11x2 – 13x – 5 = 0;
b)
c)
Hướng dẫn giải
a) Phương trình 11x2 – 13x – 5 = 0 có các hệ số a = 11; b = –13; c = –5.
Ta có: ∆ = b2 – 4ac = (–13)2 – 4.11.(–5) = 389 > 0.
Vậy phương trình 11x2 – 13x – 5 = 0 có hai nghiệm phân biệt.
b) Phương trình có các hệ số
Do b = 28 nên b’ = 14.
Ta có:
Vậy phương trình có một nghiệm (nghiệm kép).
c) Phương trình có các hệ số
Ta có:
Vậy phương trình vô nghiệm.
Bài 3. Giải các phương trình sau:
a) –7x2 + 16x + 15 = 0;
b) 9x2 + 60x + 100 = 0;
c)
d)
e) x(x – 2) = 15;
f) (2x + 7)2 – 9x = 3.
g) x(4x + 3) = –x2 + 8.
Hướng dẫn giải
a) Phương trình –7x2 + 16x + 15 = 0 có các hệ số a = –7; b = 16; c = 15.
Do b = 16 nên b’ = 8.
Ta có: ∆’ = b’2 – ac = 82 – (–7).15 = 169 > 0 và
Do đó, phương trình đã cho có hai nghiệm phân biệt là:
Vậy phương trình đã cho có hai nghiệm phân biệt là
b) Phương trình 9x2 + 60x + 100 = 0 có các hệ số a = 9; b = 60; c = 100.
Do b = 60 nên b’ = 30.
Ta có: ∆’ = b’2 – ac = 302 – 9.100 = 0.
Do đó, phương trình đã cho có nghiệm kép
Vậy phương trình đã cho có nghiệm kép là
c) Phương trình có các hệ số
Do nên
Ta có:
Do đó, phương trình đã cho có nghiệm kép
Vậy phương trình đã cho có nghiệm kép là
d) Phương trình có các hệ số
Ta có: và
Do đó, phương trình đã cho có hai nghiệm phân biệt là:
Vậy phương trình đã cho có hai nghiệm phân biệt là
e) Ta có: x(x – 2) = 15 hay x2 – 2x – 15 = 0.
Phương trình x2 – 2x – 15 = 0 có các hệ số a = 1; b = –2; c = –15.
Do b = –2 nên b’ = –1.
Ta có: ∆’ = b’2 – ac = (–1)2 – 1.(–15) = 16 > 0 và
Do đó, phương trình x2 – 2x – 15 = 0 có hai nghiệm phân biệt là:
Vậy phương trình đã cho có hai nghiệm phân biệt là x = 5 và x = –3.
f) Ta có: (2x + 7)2 – 9x = 3
4x2 + 28x + 49 – 9x – 3 = 0
4x2 + 19x + 46 = 0.
Phương trình 4x2 + 19x + 46 = 0 có các hệ số a = 4; b = 19; c = 46.
Ta có: ∆ = b2 – 4ac = 192 – 4.4.46 = –375 < 0.
Do đó phương trình 4x2 + 19x + 46 = 0 vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
g) Ta có: x(4x + 3) = –x2 + 8
4x2 + 3x + x2 – 8 = 0
5x2 + 3x – 8 = 0.
Phương trình 5x2 + 3x – 8 = 0 có các hệ số a = 5; b = 3; c = –8.
Ta có: ∆ = b2 – 4ac = 32 – 4.5.(–8) = 169 > 0 và
Do đó, phương trình 5x2 + 3x – 8 = 0 có hai nghiệm phân biệt là:
Vậy phương trình đã cho có hai nghiệm phân biệt là
Bài 4. Không tính ∆, giải các phương trình sau:
a) –x2 + 7x – 6 = 0;
b) 5x2 + 8x + 3 = 0;
c) 11x2 + 18x – 45 = 0, biết phương trình có một nghiệm x1 = –3.
Hướng dẫn giải
a) Phương trình –x2 + 7x – 6 = 0 có các hệ số a = –1; b = 7; c = –6.
Suy ra a + b + c = –1 + 7 + (–6) = 0.
Do đó phương trình –x2 + 7x – 6 = 0 có nghiệm x1 = 1 và
Vậy phương trình đã cho có hai nghiệm là x1 = 1 và x2 = 6.
b) Phương trình 5x2 + 8x + 3 = 0 có các hệ số a = 5; b = 8; c = 3.
Suy ra a – b + c = 5 – 8 + 3 = 0.
Do đó phương trình 5x2 + 8x + 3 = 0 có nghiệm x1 = –1 và
Vậy phương trình đã cho có hai nghiệm là x1 = –1 và
c) Phương trình 11x2 + 18x – 45 = 0 có các hệ số a = 11; b = 18; c = –45.
Theo định lí Viète, ta có
Với x1 = –3, ta có: Suy ra
Vậy phương trình đã cho có hai nghiệm là x1 = –3 và
Bài 5. Cho phương trình x2 – 19x – 5 = 0. Gọi x1, x2 là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức:
a) A = (x1 – x2)2;
b)
c)
Hướng dẫn giải
a) Phương trình x2 – 19x – 5 = 0 có các hệ số a = 1; b = –19; c = –5.
Ta có: ∆ = b2 – 4ac = (–19)2 – 4.1.(–5) = 381 > 0.
Do đó phương trình đã cho có hai nghiệm phân biệt x1, x2.
Theo định lí Viète, ta có:
Ta có
Vậy A = 381.
b) Ta có
Vậy
Vậy C = 692.
Bài 6. Động năng (tính bằng J) của một quả bóng rơi với tốc độ v(m/s) được tính bằng công thức
a) Tính động năng của quả bóng đạt được khi nó rơi với tốc độ lần lượt là 5 m/s, 9 m/s (làm tròn kết quả đến hàng phần trăm).
b) Tính tốc độ rơi của quả bóng tại thời điểm quả bóng đạt được động năng 50 J.
Hướng dẫn giải
a) Với v = 5 (m/s), ta có: (J).
Với v = 9 (m/s), ta có: (J).
Vậy động năng của quả bóng đạt được khi nó rơi với tốc độ lần lượt là 5 m/s, 9 m/s lần lượt bằng 5,56 J và 18 J.
b) Với K = 50 (J), ta có:
Suy ra v2 = 225 = 152 = (–15)2
Do đó v = 15 (nhận) hoặc v = –15 (loại).
Vậy tốc độ rơi của quả bóng tại thời điểm quả bóng đạt được động năng 50 J là 15 m/s.
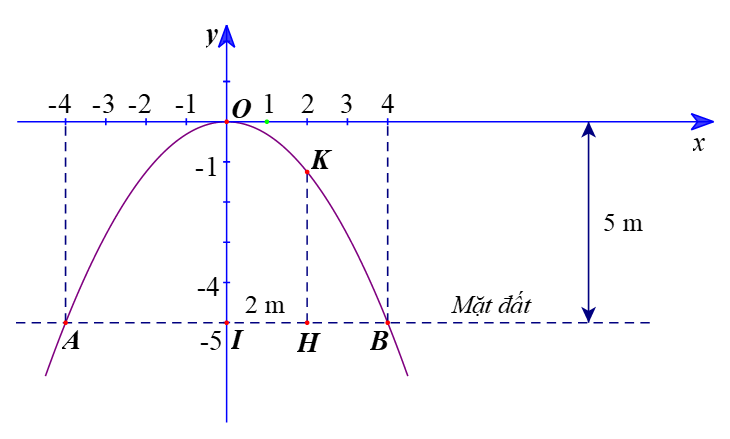
Bài 7. Một cổng vòm được thiết kế dạng parabol y = ax2 (a ≠ 0) như hình bên dưới. Biết chiều rộng của chân cổng là AB = 8 m và chiều cao của cổng là OI = 5 m.
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa I của cổng vòng 2 m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m và chiều cao 3,5 m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Hướng dẫn giải
a) Ta có và yB = yI = –OI = –5.
Suy ra tọa độ B(4; –5).
Vì B(4; –5) thuộc đồ thị hàm số đã cho nên ta có:
–5 = a.42 hay 16a = –5, suy ra (thỏa mãn).
Khi đó hàm số đã cho là
Ta có xK = xH = 2 và yH = yI = –5.
Với xK = 2, ta có
Suy ra tọa độ
Khi đó độ dài đoạn HK là:
Vậy và
b) Vì chiều cao của xe tải thấp hơn độ cao của đoạn HK (do 3,5 m < 3,75 m) và chiều rộng của xe tải bằng độ dài đoạn IH (2 m) nên xe tải có chiều rộng 2 m và chiều cao 3 m luôn đi qua được cổng vòm đó.
Bài 8. Một công ty vận tải cần điều một số xe tải để chở 1 026 tấn hàng. Khi đến kho hàng thì có 2 xe bị hỏng nên để chở hết số hàng thì mỗi xe còn lại phải chở thêm 1,5 tấn so với dự định ban đầu. Hỏi số xe dự định điều đến chở hàng là bao nhiêu? Biết rằng khối lượng hàng chở ở mỗi xe là như nhau và công ty vận tải điều đi không quá 50 xe tải.
Hướng dẫn giải
Gọi x là số xe công ty vận tải dự định điều đi để chở hàng (0 < x ≤ 50 và x ∈ ℕ).
Khi đó, số tấn hàng mỗi xe phải chở là (tấn hàng).
Vì có 2 xe bị hỏng nên số xe hàng còn lại là x – 2 (xe) và số tấn hàng mỗi xe phải chở là (tấn hàng).
Lúc này, mỗi xe còn lại phải chở thêm 1,5 tấn so với dự định ban đầu nên ta có phương trình:
Giải phương trình:
1 026x = 1 026(x – 2) + 1,5.x(x – 2)
1 026x = 1 026x – 2 052 + 1,5x2 – 3x
1,5x2 – 3x – 2 052 = 0
x2 – 2x – 1 368 = 0.
Phương trình (1) có các hệ số a = 1; b = –2; c = –1 368.
Do b = –2 nên b’ = –1.
Ta có: ∆’ = b’2 – ac = (–1)2 – 1.(–1 368) = 1 369 > 0 và
Do đó, phương trình (1) có hai nghiệm phân biệt là:
Ta thấy chỉ có giá trị x1 = 38 thỏa mãn điều kiện 0 < x ≤ 50 và x ∈ ℕ.
Vậy số xe dự định được điều đến chở hàng là 38 chiếc xe.
Bài 9. Một bể bơi hình chữ nhật có diện tích 90 m2 và chu vi 42 m. Tính chiều dài, chiều rộng của bể bơi đó.
Hướng dẫn giải
Nửa chu vi của bể bơi là: 42 : 2 = 21 (m). Do đó tổng của chiều dài và chiều rộng bể bơi bằng 21 mét.
Lại có diện tích của bể bơi là 90 m2, tức là tích của chiều dài và chiều rộng bể bơi bằng 90 m2.
Chiều dài và chiều rộng của bể bơi có tổng bằng 21 và tích bằng 90 nên hai độ dài này là hai nghiệm của phương trình: x2 – 21x + 90 = 0. (1)
Phương trình (1) có các hệ số a = 1; b = –21; c = 90.
Ta có: ∆ = b2 – 4ac = (–21)2 – 4.1.90 = 81 > 0 và
Do đó, phương trình (1) có hai nghiệm phân biệt là:
Vậy chiều dài, chiều rộng của bể bơi đó lần lượt là 15 m và 6 m (do chiều rộng nhỏ hơn chiều dài)
Học tốt Toán 9 Chương 7
Các bài học để học tốt Bài tập cuối chương 7 Toán lớp 9 hay khác:
Xem thêm tóm tắt lý thuyết Toán lớp 9 Cánh diều hay khác:
Lý thuyết Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Lý thuyết Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn
Xem thêm các tài liệu học tốt lớp 9 hay khác:
- Giải sgk Toán 9 Cánh diều
- Giải SBT Toán 9 Cánh diều
- Giải lớp 9 Cánh diều (các môn học)
- Giải lớp 9 Kết nối tri thức (các môn học)
- Giải lớp 9 Chân trời sáng tạo (các môn học)
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải sgk Toán 9 Tập 1 & Tập 2 của chúng tôi được biên soạn bám sát nội dung sgk Toán 9 Cánh diều (NXB Đại học Sư phạm).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều




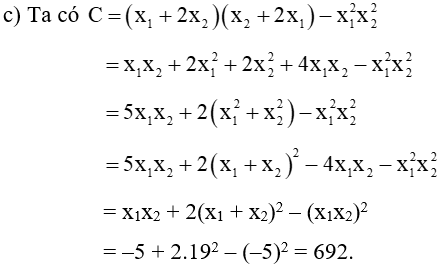



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

