Tổng hợp lý thuyết Toán 9 Chương 1 Cánh diều

Tổng hợp lý thuyết Toán 9 Chương 1: Phương trình và hệ phương trình bậc nhất sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 1.

Tổng hợp lý thuyết Toán 9 Chương 1 Cánh diều

Tổng hợp lý thuyết Toán 9 Chương 1

1. Phương trình tích có dạng (ax + b)(cx + d) = 0 (a ≠ 0, c ≠ 0)

Các bước giải phương trình tích (ax + b)(cx + d) = 0 với a ≠ 0 và c ≠ 0:

Bước 1. Giải hai phương trình bậc nhất: ax + b = 0 và cx + d = 0.

Bước 2. Kết luận nghiệm: Lấy tất cả các nghiệm của hai phương trình bậc nhất vừa giải được ở Bước 1.

2. Phương trình chứa ẩn ở mẫu

⦁ Điều kiện xác định của phương trình chứa ẩn ở mẫu:

Trong phương trình chứa ẩn ở mẫu, điều kiện của ẩn để tất cả các mẫu thức trong phương trình đều khác 0 được gọi là điều kiện xác định của phương trình.

⦁ Các bước giải phương trình chứa ẩn ở mẫu:

Bước 1. Tìm điều kiện xác định của phương trình

Bước 2. Quy đồng mẫu thức hai về của phương trình rồi khử mẫu

Bước 3. Giải phương trình vừa tìm được

Bước 4. Kết luận nghiệm: Trong các giá trị của ẩn tìm được ở Bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

3. Phương trình bậc nhất hai ẩn

– Khái niệm: Phương trình bậc nhất hai ẩn x, y là hệ thức dạng ax + by = c, trong đó a, b, c là những số cho trước, a ≠ 0 hoặc b ≠ 0.

– Khái niệm nghiệm của phương trình bậc nhất hai ẩn:

Cho phương trình bậc nhất hai ẩn x, y:    ax + by = c.

Nếu ax₀ + by₀ = c là một khẳng định đúng thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình ax + by = c.

Chú ý:

⦁ Trong mặt phẳng tọa độ Oxy, mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x₀; y₀) được biểu diễn bởi điểm có tọa độ (x₀; y₀).

⦁ Ta cũng áp dụng được quy tắc chuyển vế, quy tắc nhân đã biết ở phương trình bậc nhất một ẩn để biến đổi phương trình bậc nhất hai ẩn.

Nhận xét:

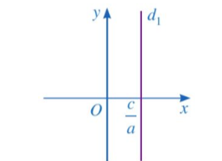
⦁ Mỗi nghiệm của phương trình ax + 0y = c hay ax = c với a ≠ 0, được biểu diễn bởi một điểm có tọa độ $\left(\frac{c}{a};y_0\right)$ (y₀ ∈ ℝ) nằm trên đường thẳng $d_1:x=\frac{c}{a}.$ Đường thẳng d₁ là đường thẳng đi qua điểm $\frac{c}{a}$ trên trục Ox và vuông góc với trục Ox (Hình vẽ):

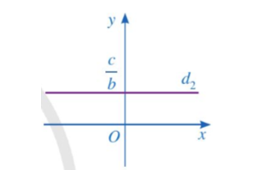
⦁ Mỗi nghiệm của phương trình 0x + by = c hay by = c với a ≠ 0, được biểu diễn bởi một điểm có tọa độ $\left(x_0;\frac{c}{b}\right)$ (x₀ ∈ ℝ) nằm trên đường thẳng $d_2:y=\frac{c}{b}.$ Đường thẳng d₂ là đường thẳng đi qua điểm $\frac{c}{b}$ trên trục Oy và vuông góc với trục Oy (Hình vẽ):

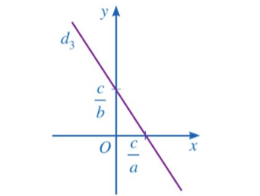
⦁ Mỗi nghiệm của phương trình ax + by = c với a ≠ 0, b ≠ 0, được biểu diễn bởi một điểm nằm trên đường thẳng $d_3:y=-\frac{a}{b}x+\frac{c}{b}.$ Đường thẳng d₃ là đồ thị của hàm số $d_3:y=-\frac{a}{b}x+\frac{c}{b}.$ (Hình vẽ):

4. Hệ hai phương trình bậc nhất hai ẩn

– Khái niệm: Hệ hai phương trình bậc nhất hai ẩn có dạng $\left\{\begin{array}{l}ax+by=c\\ a^{\text{'}}x+b^{\text{'}}y=c^{\text{'}}\end{array}\right.\left(I\right),$ ở đó mỗi phương trình ax + by = c và a’x + b’y = c’ đều là phương trình bậc nhất hai ẩn.

– Khái niệm nghiệm của hệ hai phương trình bậc nhất hai ẩn: Nếu cặp số (x₀; y₀) là nghiệm của từng phương trình trong hệ (I) thì cặp số (x₀; y₀) được gọi là nghiệm của hệ (I).

– Khái niệm giải hệ hai phương trình bậc nhất hai ẩn: Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó.

5. Giải hệ phương trình bằng phương pháp thế

Ta có thể giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế theo các bước sau:

Bước 1. (Thế) Từ một phương trình của hệ đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại của hệ để được phương trình một ẩn.

Bước 2. (Giải phương trình một ẩn) Giải phương trình (một ẩn) nhận được ở Bước 1 để tìm giá trị của ẩn đó.

Bước 3. (Tìm ẩn còn lại và kết luận) Thay giá trị vừa tìm được của ẩn đó ở Bước 2 vào biểu thức biểu diễn một ẩn theo ẩn kia ở Bước 1 để tìm giá trị của ẩn còn lại. Từ đó, ta tìm được nghiệm của hệ phương trình đã cho.

Chú ý: Hệ phương trình bậc nhất hai ẩn có thể có nghiệm duy nhất hoặc vô nghiệm hoặc vô số nghiệm.

6. Giải hệ phương trình bằng phương pháp cộng đại số

Ta có thể giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số theo các bước sau:

Bước 1. (Làm cho hai hệ số của một ẩn nào đó bằng nhau hoặc đối nhau) Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

Bước 2. (Đưa về phương trình một ẩn) Cộng (hay trừ) từng vế hai phương trình của hệ phương trình nhận được ở Bước 1 để nhận được một phương trình mà hệ số của một trong hai ẩn bằng 0, tức là nhận được phương trình một ẩn. Giải phương trình một ẩn đó.

Bước 3. (Tìm ẩn còn lại và kết luận) Thay giá trị vừa tìm được ở Bước 2 vào một trong hai phương trình của hệ đã cho để tìm giá trị của ẩn còn lại. Từ đó, ta tìm được nghiệm của hệ phương trình đã cho.

Bài tập Bài tập cuối chương 1

I. Bài tập trắc nghiệm

Bài 1. Tất cả các nghiệm của phương trình (x + 3)(2x – 6) = 0 là

A. x = –3.

B. x = 3.

C. x = 3 và x = –3.

D. x = 2.

Hướng dẫn giải

Đáp án đúng là: C

Để giải phương trình (x + 3)(2x – 6) = 0, ta giải hai phương trình sau:

⦁ x + 3 = 0

         x = –3.

⦁ 2x – 6 = 0

         2x = 6

           x = 3.

Vậy phương trình đã cho có hai nghiệm là x = 3 và x = –3.

Bài 2. Điều kiện xác định của phương trình $\frac{x}{2x-1}+\frac{3}{x+5}=\frac{x}{\left(2x-1\right)\left(x+5\right)}$ là

A. x ≠ $\frac{1}{2}.$

B. x ≠ $\frac{1}{2}$ và x ≠ –5.

C. x ≠ 0.

D. x ≠ –5.

Hướng dẫn giải

Đáp án đúng là: B

Điều kiện xác định của phương trình đã cho là 2x – 1 ≠ 0 và x + 5 ≠ 0 hay x ≠ $\frac{1}{2}$ và x ≠ –5.

Bài 3. Phương trình x – 1 = m + 4 có nghiệm lớn hơn 1 với

A. m ≥ –4.

B. m ≤ 4.

C. m > –4.

D. m < –4.

Hướng dẫn giải

Đáp án đúng là: C

Xét phương trình:

x – 1 = m + 4

x = m + 5.

Để phương trình có nghiệm lớn hơn 1 tức x > 1 thì m + 5 > 1, suy ra m > –4.

Bài 4. Phương trình nào sau đât không phải là phương trình bậc nhất hai ẩn?

A. x – 5y = –3.

B. –2x + 0y = 0.

C. 0x – 2y = 1.

D. 0x + 0y = 1.

Hướng dẫn giải

Đáp án đúng là: D

Phương trình bậc nhất hai ẩn có dạng ax + by = c với a ≠ 0 hoặc b ≠ 0.

Vậy phương trình 0x + 0y = 1 không phải là phương trình bậc nhất hai ẩn.

Bài 5. Cặp số nào sau đây là nghiệm của phương trình 5x + 4y = 8?

A. (–2; 1).

B. (0; 2).

C. (–1; 0).

D. (4; 3).

Hướng dẫn giải

Đáp án đúng là: B

Xét phương trình 5x + 4y = 8:

⦁ Thay x = –2 và y = 1, ta có: 5.(–2) + 4.1 = –2 ≠ 8.

⦁ Thay x = 0 và y = 2, ta có: 5.0 + 4.2 = 8.

⦁ Thay x = –1 và y = 0, ta có: 5.(–1) + 4.0 = –5 ≠ 8.

⦁ Thay x = 4 và y = 3, ta có: 5.4 + 4.3 = 32 ≠ 8.

Vậy (0; 2) là nghiệm của phương trình đã cho.

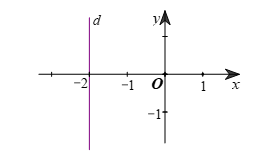
Bài 6. Đường thẳng d trong hình vẽ dưới đây biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn nào?

A. –2x + 0y = 0.

B. y = –2.

C. 0x + 2y = –4.

D. 2x + 0y = –4.

Hướng dẫn giải

Đáp án đúng là: D

Đường thẳng d trong hình vẽ là đường thẳng đi qua điểm –2 trên trục Ox và vuông góc với trục Ox nên đường thẳng d biểu diễn tất cả các nghiệm của phương trình x = –2.

⦁ Xét phương án A: ta có phương trình –2x + 0y = 0, hay x = 0 (loại).

⦁ Xét phương án B: ta có phương trình y = –2 (loại).

⦁ Xét phương án C: ta có phương trình 0x + 2y = –4, hay y = –2 (loại).

⦁ Xét phương án D: ta có phương trình 2x + 0y = –4, hay x = –2.

Vậy ta chọn phương án D.

Bài 7. Đường thẳng biểu diễn tất cả các nghiệm của phương trình x – 3y = 2 là đường thẳng

A. vuông góc với trục tung.

B. vuông góc với trục hoành.

C. đi qua gốc tọa độ.

D. đi qua điểm A(–1; –1).

Hướng dẫn giải

Đáp án đúng là: D

Thay x = –1 và y = –1 vào phương trình ta có:

–1 – 3.(–1) = 2.

Vậy đường thẳng x – 3y = 2 đi qua điểm A(–1; –1).

Bài 8. Cặp số nào sau đây là nghiệm của hệ phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}4x-5y=3\\ 3x-y=16\end{array}\right.?$

A. (–1; 3).

B. (2; 1).

C. (7; 5).

D. (5; –1).

Hướng dẫn giải

Đáp án đúng là: C

 ⦁ Thay x = –1 và y = 3 vào mỗi phương trình trong hệ, ta có:

4.(–1) – 5.3 = –19 ≠ 3;

3.(–1) – 3 = –6 ≠ 16.

Do đó cặp số (–1; 3) không là nghiệm của mỗi phương trình trong hệ.

Vậy cặp số (–1; 3) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 2 và y = 1 vào mỗi phương trình trong hệ, ta có:

4.2 – 5.1 = 3;

3.2 – 1 = 5 ≠ 16.

Do đó cặp số (2; 1) không là nghiệm của phương trình thứ hai trong hệ.

Vậy cặp số (2; 1) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 7 và y = 5 vào mỗi phương trình trong hệ, ta có:

4.7 – 5.5 = 3;

3.7 – 5 = 16.

Suy ra cặp số (7; 5) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (7; 5) là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 5 và y = –1 vào mỗi phương trình trong hệ, ta có:

4.5 – 5.(–1) = 25 ≠ 3;

3.5 – (–1) = 16.

Do đó cặp số (5; –1) không là nghiệm của phương trình thứ nhất trong hệ.

Vậy cặp số (5; –1) không là nghiệm của hệ phương trình đã cho.

Ta chọn phương án C.

Bài 9. Khẳng định nào sau đây là đúng?

Hệ phương trình $\left\{\begin{array}{l}0,6x+0,3y=1,8\\ 2x+y=-6\end{array}\right.$

A. có một nghiệm.

B. vô nghiệm.

C. có vô số nghiệm.

D. có hai nghiệm.

Hướng dẫn giải

Đáp án đúng là: B

Xét hệ phương trình $\left\{\begin{array}{l}0,6x+0,3y=1,8\left(1\right)\\ 2x+y=-6\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có:    y = –6 – 2x. (*)

Thế vào phương trình (1) ta được: 0,6x + 0,3.(–6 – 2x) = 1,8. (**)

Giải phương trình (**):

0,6x + 0,3.(–6 – 2x) = 1,8

0,6x – 1,8 – 0,6x = 1,8

0x = 3,6.

Do đó phương trình (**) vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

Bài 10. Khẳng định nào sau đây là đúng?

Hệ phương trình $\left\{\begin{array}{l}1,5x-0,6y=0,3\\ -2x+y=-2\end{array}\right.$

A. có nghiệm là (0; –0,5).

B. có nghiệm là (1; 0).

C. có nghiệm là (–3; –8).

D. vô nghiệm.

Hướng dẫn giải

Đáp án đúng là: C

Xét hệ phương trình $\left\{\begin{array}{l}1,5x-0,6y=0,3\left(1\right)\\ -2x+y=-2\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có:    y = 2x – 2. (*)

Thế vào phương trình (1) ta được: 1,5x – 0,6.(2x – 2) = 0,3. (**)

Giải phương trình (**):

1,5x – 0,6.(2x – 2) = 0,3

1,5x – 1,2x + 1,2 = 0,3

0,3x = –0,9

     x = –3.

Thay x = –3 vào phương trình (*), ta có:

y = 2.(–3) – 2 = –8.

Vậy hệ phương trình đã cho có nghiệm duy nhất (–3; –8).

2. Bài tập tự luận

Bài 1. Giải các phương trình sau:

a) x(22x – 12) = 0;

b) (4x – 1)² – 9x² = 0.

Hướng dẫn giải

a) (x + 21)(22x – 12) = 0

Để giải phương trình đã cho, ta giải hai phương trình sau:

⦁ x + 21 = 0

           x = –21;

⦁ 22x – 12 = 0

            22x = 12

                 $x=\frac{12}{22}$

                 $x=\frac{6}{11}.$

Vậy phương trình đã cho có hai nghiệm là x = –21 và $x=\frac{6}{11}.$

b) (4x – 1)² – 9x² = 0

(4x – 1)² – (3x)² = 0

(4x – 1 – 3x)(4x – 1 + 3x) = 0

(x – 1)(7x – 1) = 0.

Để giải phương trình trên, ta giải hai phương trình sau:

⦁ x – 1 = 0

        x = 1;

⦁ 7x – 1 = 0

         7x = 1

          $x=\frac{1}{7}.$

Vậy phương trình đã cho có hai nghiệm là x = 1 và $x=\frac{1}{7}.$

Bài 2. Giải các phương trình sau:

a) $\frac{x}{2x-5}=\frac{4}{3};$

b) $\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{\left(x-1\right)\left(x+1\right)}.$

Hướng dẫn giải

a) Điều kiện xác định: $x\ne \frac{5}{2}.$

$\frac{x}{2x-5}=\frac{4}{3}$

$\frac{3x}{3\left(2x-5\right)}=\frac{4\left(2x-5\right)}{3\left(2x-5\right)}$

3x = 4(2x – 5)

3x = 8x – 20

–5x = –20

    x = 4.

Ta thấy x = 4 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = 4.

b) Điều kiện xác định: x ≠ 1 và x ≠ –1.

$\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{\left(x-1\right)\left(x+1\right)}$

$\frac{{\left(x+1\right)}^2}{\left(x-1\right)\left(x+1\right)}-\frac{{\left(x-1\right)}^2}{\left(x-1\right)\left(x+1\right)}=\frac{4}{\left(x-1\right)\left(x+1\right)}$

(x + 1)² – (x – 1)² = 4

x² + 2x + 1 – (x² – 2x + 1) = 4

x² + 2x + 1 – x² + 2x – 1 = 4

4x = 4

  x = 1.

Ta thấy x = 1 không thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho vô nghiệm.

Bài 3. Một người đi xe đạp từ A đến B cách nhau 24 km. Khi từ B trở về A (cùng cung đường khi đi từ A đến B), người đó tăng vận tốc thêm 4 km/h so với lúc đi nên lúc về mất ít thời gian hơn so với lúc đi là 30 phút. Tính vận tốc của người xe đạp khi đi từ A đến B.

Hướng dẫn giải

Đổi 30 phút $=\frac{1}{2}$ giờ.

Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h, x > 0).

Thời gian người đó đi từ A đến B là $\frac{24}{x}$ (giờ).

Khi từ B trở về A, người đó tăng vận tốc thêm 4 km/h so với lúc đi nên lúc trở về, vận tốc của người đó là: x + 4 (km/h).

Thời gian người đó từ B trở về A là: $\frac{24}{x+4}$ (giờ).

Theo bài, lúc về mất ít thời gian hơn so với lúc đi là 30 phút nên ta có phương trình: $\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}.$

Giải phương trình:

$\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}$

$\frac{24\cdot 2\left(x+4\right)}{2x\left(x+4\right)}-\frac{24\cdot 2x}{2x\left(x+4\right)}=\frac{x\left(x+4\right)}{2x\left(x+4\right)}$

24.2(x + 4) – 24.2x = x(x + 4)

48x + 192 – 48x = x² + 4x

192 = x² + 4x

x²– 12x + 16x – 192 = 0

x(x – 12) + 16(x – 12) = 0

(x – 12)(x + 16) = 0

x – 12 = 0 hoặc x + 16 = 0

x = 12 hoặc x = –16.

Ta thấy chỉ có x = 12 thỏa mãn điều kiện x > 0.

Vậy vận tốc người xe đạp khi đi từ A đến B là 12 km/h.

Bài 4. Hai bến sông A và B cách nhau 40 km. Cùng một lúc với ca nô xuôi từ bến A có một chiếc bè trôi từ bến A với vận tốc 3 km/h. Sau khi đến bến B, ca nô ngược dòng quay trở về bến A ngay và gặp bè, khi đó bè đã trôi được 8 km. Tính vận tốc riêng của ca nô.

Hướng dẫn giải

Gọi vận tốc riêng ca nô là x (km/h), x > 3.

Vận tốc của bè trôi xuôi dòng từ A đến B chính là vận tốc của dòng nước, nên vận tốc ca nô xuôi dòng là x + 3 (km/h).

Thời gian ca nô xuôi dòng từ A đến B là $\frac{40}{x+3}$ (giờ).

Vận tốc ca nô ngược dòng là x – 3 (km/h).

Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là: 40 – 8 = 32 (km).

Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: $\frac{32}{x-3}$ (giờ).

Thời gian bè trôi là: $\frac{8}{3}$ (giờ).

Theo bài, ta có phương trình:

$\frac{40}{x+3}+\frac{32}{x-3}=\frac{8}{3}$

$\frac{5}{x+3}+\frac{4}{x-3}=\frac{1}{3}$

$\frac{5\cdot 3\left(x-3\right)}{3\left(x+3\right)\left(x-3\right)}+\frac{4\cdot 3\left(x+3\right)}{3\left(x+3\right)\left(x-3\right)}=\frac{1\cdot \left(x+3\right)\left(x-3\right)}{3\left(x+3\right)\left(x-3\right)}$

5.3(x – 3) + 4.3(x + 3) = (x + 3)(x – 3)

15x – 45 + 12x + 36 = x² – 9

27x – 9 = x² – 9

x² – 27x = 0

x(x – 27) = 0

x = 0 hoặc x – 27 = 0

x = 0 hoặc x = 27.

Ta thấy chỉ x = 27 thỏa mãn điều kiện x > 3.

Vậy vận tốc riêng của cano là: 27 km/h.

Bài 5. Xét trò ném đồng xu vào trong vòng tròn như hình vẽ dưới đây:

– Lượt chơi thứ nhất (ném đồng xu 2 lần): một đồng xu rơi vào phần trong (hình tròn màu trắng), một đồng xu rơi vào phần ngoài (hình vành khăn màu đen); tổng số điểm đạt được là 17 (điểm).

– Lượt chơi thứ hai (ném đồng xu 5 lần): hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài; tổng số điểm đạt được là 41 (điểm).

Gọi x, y lần lượt là số điểm ấn định cho phần trong và phần ngoài.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (10; 7) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) – Lượt chơi thứ nhất có một đồng xu rơi vào phần trong và một đồng xu rơi vào phần ngoài, đạt được 17 điểm nên ta có phương trình: x + y = 17.

– Lượt chơi thứ hai có hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài, đạt được 41 điểm nên ta có phương trình: 2x + 3y = 41.

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x+y=17\\ 2x+3y=41.\end{array}\right.$

b) Thay x = 10 và y = 7 vào mỗi phương trình trong hệ ở câu a, ta có:

10 + 7 = 17;

2.10 + 3.7 = 41.

Suy ra cặp số (10; 7) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (10; 7) là nghiệm của hệ phương trình ở câu a.

Bài 6. Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}x+y=5\\ 3x-2y=5.\end{array}\right.$

b) $\left\{\begin{array}{l}x+7y=14\\ 2x+14y=28.\end{array}\right.$

c) $\left\{\begin{array}{l}\frac{3}{2}x-2y=8\\ 3x-4y=11.\end{array}\right.$

Hướng dẫn giải

a) $\left\{\begin{array}{l}x+y=5\left(1\right)\\ 3x-2y=5\left(2\right).\end{array}\right.$

Từ phương trình (1), ta có:    x = 5 – y. (*)

Thế vào phương trình (2) ta được: 3.(5 – y) – 2y = 5. (**)

Giải phương trình (**):

3.(5 – y) – 2y = 5

15 – 3y – 2y = 5

15 – 5y = 5

–5y = –10

    y = 2.

Thay y = 2 vào phương trình (*), ta có:

x = 5 – 2 = 3.

Vậy hệ phương trình đã cho có nghiệm duy nhất (3; 2).

b) $\left\{\begin{array}{l}x+7y=14\left(3\right)\\ 2x+14y=28.\left(4\right)\end{array}\right.$

Từ phương trình (3), ta có:    x = 14 – 7y. (***)

Thế vào phương trình (4) ta được: 2.(14 – 7y) + 14y = 28. (****)

Giải phương trình (****):

2.(14 – 7y) + 14y = 28

28 – 14y + 14y = 28

0y = 0.

Do đó phương trình (****) có vô số nghiệm.

Vậy hệ phương trình đã cho có vô số nghiệm.

c) $\left\{\begin{array}{l}\frac{3}{2}x-2y=8\left(5\right)\\ 3x-4y=11\left(6\right)\end{array}\right.$

Từ phương trình (5), ta có:    $2y=\frac{3}{2}x-8,$ suy ra $y=\frac{3}{4}x-4.\left(7\right)$

Thế vào phương trình (6) ta được: $3x-4\cdot \left(\frac{3}{4}x-4\right)=11.\left(8\right)$

Giải phương trình (8):

$3x-4\cdot \left(\frac{3}{4}x-4\right)=11$

3x – 3x + 16 = 11

0x = –5.

Do đó phương trình (8) vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

Bài 7. Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) $\left\{\begin{array}{l}-0,5x+0,5y=1\\ -2x+2y=8.\end{array}\right.$

b) $\left\{\begin{array}{l}2x+6y=-7\\ 5x-2y=-9.\end{array}\right.$

c) $\left\{\begin{array}{l}3x-5y=2\\ -6x+10y=-4.\end{array}\right.$

Hướng dẫn giải:

a) $\left\{\begin{array}{l}-0,5x+0,5y=1\\ -2x+2y=8.\end{array}\right.$

Nhân hai vế của phương trình (1a) với 4, ta được hệ phương trình sau: $\left\{\begin{array}{l}-2x+2y=4\left(3a\right)\\ -2x+2y=8\left(4a\right)\end{array}\right.$

Trừ từng vế hai phương trình (3a) và (4a), ta nhận được phương trình:

0x + 0y = 12.

Phương trình trên vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

b) $\left\{\begin{array}{l}2x+6y=-7\left(1b\right)\\ 5x-2y=-9\left(2b\right)\end{array}\right.$

Nhân hai vế của phương trình (2b) với 3, ta được hệ phương trình sau: $\left\{\begin{array}{l}2x+6y=-7\left(3b\right)\\ 15x-6y=-27\left(4b\right)\end{array}\right.$

Cộng từng vế hai phương trình (3b) và (4b), ta nhận được phương trình:

17x = –34, tức là x = –2.

Thay x = –2 vào phương trình (2b), ta có: 5.(–2) – 2y = –9. (5b)

Giải phương trình (5b):

5.(–2) – 2y = –9

–10 – 2y = –9

–2y = 1

   $y=-\frac{1}{2}.$

Vậy hệ phương trình đã cho có nghiệm duy nhất $\left(-2;-\frac{1}{2}\right).$

c) $\left\{\begin{array}{l}3x-5y=2\left(1c\right)\\ -6x+10y=-4\left(2c\right)\end{array}\right.$

Nhân hai vế của phương trình (1c) với 2, ta được hệ phương trình sau: $\left\{\begin{array}{l}6x-10y=4\left(3c\right)\\ -6x+10y=-4\left(4c\right)\end{array}\right.$

Cộng từng vế hai phương trình (3c) và (4c), ta nhận được phương trình:

0x + 0y = 0.

Phương trình trên vô số nghiệm.

Vậy hệ phương trình đã cho có vô số nghiệm.

Bài 8. Trong một đợt khuyến mãi, siêu thị giảm giá cho mặt hàng A là 20% và mặt hàng B là 15% so vối giá niêm yết. Một khách hàng mua 2 món hàng A và 1 món hàng B thì phải trả số tiền là 362 000 đồng. Nhưng nếu mua trong khung giờ vàng thì mặt hàng A được giảm giá 30% và mặt hàng B được giảm giá 25% so với giá niêm yết. Một khách hàng mua 3 món hàng A và 2 món hàng B trong khung giờ vàng nên phải trả số tiền là 552 000 đồng. Tính giá niêm yết của mỗi mặt hàng A và B.

Hướng dẫn giải

Gọi giá niêm yết của mặt hàng A và B lần lượt là x, y (đồng) (x > 0, y > 0).

Giá của mặt hàng A sau khi giảm giá 20% là x.(100% – 20%) = 0,8x (đồng).

Giá của mặt hàng B sau khi giảm giá 15% là y.(100% – 15%) = 0,85y (đồng).

Khi đó, số tiền khách hàng phải trả khi mua 2 món hàng A và 1 món hàng B là: 2.0,8x + 0,85y (đồng).

Theo bài, ta có phương trình:

2.0,8x + 0,85y = 362 000 hay 1,6x + 0,85y = 362 000. (1)

Giá của mặt hàng A sau khi giảm giá 30% là x.(100% – 30%) = 0,7x (đồng).

Giá của mặt hàng B sau khi giảm giá 25% là y.(100% – 25%) = 0,75y (đồng).

Khi đó, số tiền khách hàng phải trả khi mua 3 món hàng A và 2 món hàng B là: 3.0,7x + 2.0,75y (đồng).

Theo bài, ta có phương trình:

3.0,7x + 2.0,75y = 552 000 hay 2,1x + 1,5y = 552 000. (2)

Ta có hệ phương trình: $\left\{\begin{array}{l}1,6x+0,85y=362000\left(1\right)\\ 2,1x+1,5y=552000\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 210 và nhân hai vế của phương trình (1) với 160, ta được hệ phương trình sau: $\left\{\begin{array}{l}336x+178,5y=76020000\left(3\right)\\ 336x+240y=88320000\left(4\right)\end{array}\right.$

Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:

–61,5y = –12 300 000, tức là y = 200 000 (thỏa mãn).

Thay y = 200 000 vào phương trình (1), ta có:

1,6x + 0,85.200 000 = 362 000. (5)

Giải phương trình (5):

1,6x + 0,85.200 000 = 362 000

1,6x + 170 000 = 362 000

1,6x = 192 000

x = 120 000 (thỏa mãn).

Do đó hệ phương trình có nghiệm duy nhất (120 000; 200 000).

Vậy giá niêm yết của mặt hàng A và B lần lượt là 120 000 đồng và 200 000 đồng.

Bài 9. Tìm các hệ số x, y để cân bằng phương trình phản ứng hóa học sau:

4Al + xO₂ → yAl₂O₃.

Hướng dẫn giải

Theo định luật bảo toàn nguyên tố đối với Al và O, ta có: $\left\{\begin{array}{l}4=2y\left(1\right)\\ 2x=3y\left(2\right)\end{array}\right.$

Giải phương trình (1):

4 = 2y

y = 2.

Thay y = 2 vào phương trình (2), ta được: 2x = 3.2.   (3)

Giải phương trình (3):

2x = 3.2

2x = 6

  x = 3.

Do đó hệ phương trình có nghiệm duy nhất (x; y) = (3; 2).

Vậy ta có phương trình sau cân bằng:

4Al + 3O₂ → 2Al₂O₃.

Học tốt Bài tập cuối chương 1

Các bài học để học tốt Bài tập cuối chương 1 Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài tập cuối chương 1

Xem thêm tóm tắt lý thuyết Toán lớp 9 Cánh diều hay khác:

• Lý thuyết Toán 9 Bài 1: Bất đẳng thức

• Lý thuyết Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn

• Tổng hợp lý thuyết Toán 9 Chương 2

• Lý thuyết Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực

• Lý thuyết Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực

Săn shopee siêu SALE :

• Sổ lò xo Art of Nature Thiên Long màu xinh xỉu
• Biti's ra mẫu mới xinh lắm
• Tsubaki 199k/3 chai
• L'Oreal mua 1 tặng 3

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---