200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 5)
Với 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit (cơ bản - phần 5) có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit (cơ bản - phần 5).
200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 5)
(199k) Học Toán 12 KNTTHọc Toán 12 CDHọc Toán 12 CTST
Bài 161: Tính tổng T tất cả các nghiệm của phương trình (x – 3)2x2-5x = 1.
Lời giải:
Bài 162: Cho phương trình 2016x2 .2017x = 2016x. Mệnh đề nào sau đây là đúng?
A. Phương trình đã cho có hai nghiệm âm phân biệt.
B. Phương trình đã cho có một nghiệm bằng 0 và một nghiệm âm.
C. Phương trình đã cho có một nghiệm bằng 0 và một nghiệm dương.
D. Phương trình đã cho có hai nghiệm trái dấu và một nghiệm bằng 0.
Lời giải:
Bài 163: giải phương trình 3.9x + 7.6x – 6.4x = 0
A. x = 1 – log2 3 B. x = -1 + log2 3 C. x = log3 2 D. x = -1
Lời giải:
Bài 163: Giải bất phương trình
A. 1 < x< 9 B. x > 1 C. x < 9 D. x > 9 hoặc x < 1
Lời giải:
Điều kiện: x ∈ R (*)
Do 2/3<0 nên Bất phương trình ⇔ x2 – 6x + 4 < 4x – 5 ⇔ x2 – 10x + 9 < 0 ⇔ 1 < x < 9
Chọn A.
Bài 164: Bất phương trình 3x2-6x-16 < 9x+2 có số nghiệm nguyên là ?
A.11 B. 9 C.10 D. 12
Lời giải:
Điều kiện: x ∈ R (*)
Ta có 9x+2 = (32)x+2 = 32(x+2) bất phương trình ⇔ 3x2-6x-16 < 32(x+2)
⇔ x2 – 6x – 16 < 2(x+2) hay x2 – 8x – 20 < 0
Do đó : -2<x<10
Mà x ∈ R ⇒ x ∈ {-1;0;1;2;3;4;5;6;7;8;9}
Chọn A.
Bài 165:
a/Giải bất phương trình 23x-1 > 5
b/ Giải bất phương trình (e – 2)2x-1 > 2
Lời giải:
Bài 166:
a/Giải bất phương trình 2x + 2x +1 > 3x +1 + 3x +2
b/Giải bất phương trình 2x .3x +1 > 5
Lời giải:
Bài 167: Bất phương trình 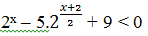
A. 3 B.6 C. 4 D. 5
Lời giải:
Bài 168: Bất phương trình 4x + 32x > 2.6x
A. x > 0 B. x ≠ 0 C. -1 < x < 0 D. 0 < x < 1
Lời giải:
Điều kiện: x ∈ R (*)
Bất phương trình ⇔ (2x)2 + (3x)2 > 2.2x.3x ⇔ (2x – 3x)2 > 0 ⇔ 2x – 3x ≠ 0 ⇔ x ≠ 0
Chọn B.
Bài 169: Tìm tập nghiệm S của phương trình log3(2x + 1) – log3(x – 1) = 1
A. S = {4} B.S = {3} C. S = {-2} D. 4
Lời giải:
Vậy nghiệm duy nhất cuả phương trình là x = 4
Chọn A.
Bài 170:
a/Tập nghiệm của phương trình log2(3x – 7) = 3 là
A. {1}. B. {-2}. C. {5}. D. {-3}
b/ Tập nghiệm của phương trình log2 x = 5 là
A. {5}. B. {1}. C. {25}. D. {32}
Lời giải:
a/ Điều kiện
Pt log2 (3x – 7) = 3 ⇔ 3x – 7 = 23 ⇔ x = 5 thỏa mãn điều kiện.
Vậy phương trình có tập nghiệm là S = {5}.
Chọn C.
b/ Điều kiện x > 5
Phương trình log2 x = 5 ⇔ x = 25 ⇔ x = 32 thỏa mãn điều kiện.
Chọn D.
Bài 171: Phương trình log2 (x2 + 2x + 1) = 0 có bao nhiêu nghiệm:
A. 1. B. 2. C. 0. D. 3
Lời giải:
Điều kiện x2 + 2x + 1 > 0 ⇔ x ≠ 1
Phương trình log2 (x2 + 2x + 1) = 0 ⇔ x2 + 2x + 1 = 1 ⇔ x2 + 2x = 0 ⇔x = 0 hoặc x = -2 đều thỏa mãn điều kiện. Vậy phương trình có 2 nghiệm.
Chọn B.
Bài 172: Gọi n là số nghiệm của phương trình log2 x2 = 2log2(3x + 4). Tìm n
A. n = 0 B.n = -1 C. n = 2 D. n = 1
Lời giải:
Bài 173:
a/ Tìm số nghiệm của phương trình
A. 2. B. 0. C. 1. D. 3.
b/ Tìm số nghiệm của phương trình
A. 3. B. 2. C. 1. D. 0.
Lời giải:
Bài 174: Phương trình log2 (x + 2) + log4 x2 = 3 có nghiệm là:
A. x = -2, x = 4. B. x = 2, x = 4. C. x = 2. D. x = 0.
Lời giải:
Bài 175: Phương trình 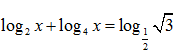
có nghiệm duy nhất x0 được biểu diễn dưới dạng 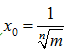
, với m,n là các số nguyên. Tính tỉ số
Lời giải:
Bài 176: Phương trình log2 (3x – 4).log2x = log2 x có tổng bình phương các nghiệm là:
A. 6. B. 5. C. 10. D. 17
Lời giải:
Bài 177: Phương trình log2 x + 2log5 x = 2 + log2 x.log5 x có tích các nghiệm là:
A. 21. B. 20. C. 22. D. 24
Lời giải:
Vậy tích 2 nghiệm của phương trình là 20.
Chọn B.
Bài 178: Tổng các nghiệm của phương trình log2 x – log x.log2(4x) + 2log2x = 0 là:
A. 100. B. 101. C. 102. D. 103
Lời giải:
Tổng các nghiệm của phương trình là 101.
Chọn B.
Bài 179: Ngiệm của phương trình logx-2 2x = 3 là nghiệm của phương trình nào trong các phương trình dưới đây?
A. 2x2-3x = 32 B.x2 + 4x – 5 = 0
C. x3 – 4x2 + 3 = 0 D. log2(x2 – 8) = 3
Lời giải:
Với x=4, thay lần lượt vào các đáp án, ta được log2(x2 – 8) = 3
Chọn D.
Bài 180:
a/ Phương trình 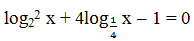
A. K = 4. B. K = 5. C. K = 6. D. K = 7.
b/ Phương trình 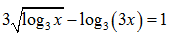
A. 1. B. 36. C. 243. D. 81.
Lời giải:
Bài 181: Cho phương trình 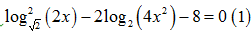
A. 3x + 5x = 6x + 2.
B. 4x2-x+22x2-x+1 – 3 = 0.
C. x2 – 3x + 2 = 0.
D. 4x2 – 9x + 2 = 0.
Lời giải:
Vậy tập hợp nghiệm của phương trình đã cho là 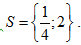
Chọn D.
Bài 182: Phương trình lg(x – 3) +lg(x – 2) = 1 – lg 5 có tất cả bao nhiêu nghiệm trên tập số thực.
A. 2 B. 3 C. 1 D. 4
Lời giải:
Bài 183: Phương trình 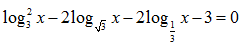
Lời giải:
Bài 184: Phương trình 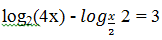
A. nghiệm B. 2 nghiệm C. 3 nghiệm D. vô nghiệm
Lời giải:
Với t = 0, ta có log2 x = 0 ⇔ x = 20 = 1
Với t = 2, ta có log2 x = 2 → x = 22 = 4
Vậy phương trình đã cho có hai nghiệm phân biệt.
Chọn B.
Bài 185:
a/ Tìm tập nghiệm của bất phương trình 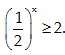
A. (-∞;-1] B. [-1;+∞) C. (-∞;-1) D. (-1;+∞)
b/ Tìm tập nghiệm S của bất phương trình 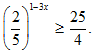
Lời giải:
Bài 186:
Lời giải:
Bài 187: Giải bất phương trình log1/2(x2 – 3x + 2) ≥ 1.
x ∈ (-∞;1). B. x ∈ [0;2). C. x∈ [0;1) ∪ (2;3]. D. x ∈ [0;2) ∪ (3;7).
Lời giải:
Bài 188: Tập nghiệm của bất phương trình 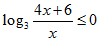
Lời giải:
Bài 189: Biết tập nghiệm S của bất phương trình log0,3(4x2) ≥ log0,3(12x – 5) là một đoạn. Gọi m, M lần lượt là giá trị nhỏ nhất, lớn nhất của tập S. Mối liên hệ giữa m và M là
A. m + M = 3 B. m + M = 2 C. M – m = 3 D. M – m = 1
Lời giải:
Bài 190:
Lời giải:
Bài 191: Tập nghiệm của bất phương trình log2 x ≤ logx 2 là
Lời giải:
Bài 192: Cho phương trình 2.5x – (m + 2)5x + 2m – 1 = 0 với m là tham số thực. Có bao nhiêu giá trị nguyên m ∈ [0;2018] để phương trình có nghiệm?
A. 2015 B. 2016 C. 2018 D. 2017
Lời giải:
Bài 193: Số nghiệm thực của phương trình 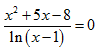
A. 3 B. 2 C. 0 D. 1
Lời giải:
Điều kiện x – 1 > 0 ⇔ x > 1.
Khi đó phương trình
Kết hợp với điều kiện suy ra nghiệm của phươn trình là: 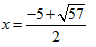
Chọn D.
Bài 194: Một người gửi số tiền 2 triệu đồng vào một ngân hàng với lãi suất 0,65%/tháng. Biết rằng nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Số tiền người đó lãnh được sau hai năm, nếu trong khoảng thời gian này không rút tiền ra và lãi suất không đổi là:
A. (2,0065)24 triệu đồng. B. (1,0065)24 triệu đồng.
C. 2.(1,0065)24 triệu đồng. D. 2.(2,0065)24 triệu đồng.
Lời giải:
Gọi số tiền gửi vào vào là M đồng, lãi suất là r/tháng.
+ Cuối tháng thứ nhất: số tiền lãi là: Mr. Khi đó số vốn tích luỹ đượclà:
T1 = M + Mr = M(1 + r).
+ Cuối tháng thứ hai: số vốn tích luỹ được là:
T2 = T1 + T1r = T1(1 + r) = M(1 + r)(1 + r) = M(1 + r)2.
+ Tương tự, cuối tháng thứ n: số vốn tích luỹ đượclà: Tn = M(1 + r)n.
Áp dụng công thức trên với M = 2, r = 0,0065, n = 24, thì số tiền người đó lãnh được sau 2 năm (24 tháng) là: T24 = 2.(1+0,0065)24 = 2.(1,0065)24 triệu đồng.
Chọn C.
Bài 195: Một người gửi số tiền M triệu đồng vào một ngân hàng với lãi suất 0,7%/tháng. Biết rằng nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Sau ba năm, người đó muốn lãnh được số tiền là 5 triệu đồng, nếu trong khoảng thời gian này không rút tiền ra và lãi suất không đổi, thì người đó cần gửi số tiền M là:
A. 3 triệu 600 ngàn đồng. B. 3 triệu 800 ngàn đồng.
C. 3 triệu 700 ngàn đồng. D. 3 triệu 900 ngàn đồng.
Lời giải:
Áp dụng công thức trên với Tn = 5, r = 0,007, n = 36, thì số tiền người đó cần gửi vào ngân hàng trong 3 năm (36 tháng) là:
Bài 196: Lãi suất gửi tiết kiệm của các ngân hàng trong thời gian qua liên tục thay đổi. Bác An gửi vào một ngân hàng số tiền 5 triệu đồng với lãi suất 0,7%/tháng. Sau sáu tháng gửi tiền, lãi suất tăng lên 0,9%/tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6%/tháng và giữ ổn định. Biết rằng nếu bác An không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Sau một năm gửi tiền, bác An rút được số tiền là (biết trong khoảng thời gian này bác An không rút tiền ra):
A. ≈5436521,164 đồng. B. ≈5468994,09 đồng.
C. ≈5452733,453 đồng. D. ≈5452771,729 đồng.
Lời giải:
Số vốn tích luỹ của bác An sau 6 tháng gửi tiền với lãi suất 0,7%/tháng là: T1 = 5.(1,007)6
triệu đồng;
Số vốn tích luỹ của bác An sau 9 tháng gửi tiền (3 tháng tiếp theo với lãi suất 0,9%/tháng) là: T2 = T1.(1,009)3 = 5.(1,007)6.(1,009)3 triệu đồng;
Do đó số tiền bác An lãnh được sau 1 năm (12 tháng) từ ngân hàng (3 tháng tiếp theo sau đó với lãi suất 0,6%/tháng) là: T = T2.(1,006)3 = 5.(1,007)6.(1,009)3.(1,006)3 triệu đồng ≈5452733,453 đồng
Chọn C.
Bài 197: (Đề thi thử Sở Thanh Hóa) Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7%/tháng theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
A. 21. B. 22. C. 23. D. 24.
Lời giải:
Bài 198: Cường độ một trận động đất M (richter) được cho bởi công thức M = logA – logA0, với A là biên độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ là
A. 2,075 độ Richter. B. 33.2 độ Richter. C. 8.9 độ Richter. D. 11 độ Richter.
Lời giải:
Cường độ trận động đất ở San Francisco là 8,3 = log A – log A0
Trận động đất khác Nam Mỹ có biên độ là 4A
Suy ra cường độ là
M = log 4A – log A0 = log 4 + log A – log A0 = log 4 + 8,3 ≈ 8,9.
Chọn C.
Bài 199: Có bao nhiêu giá trị nguyên dương của m để hàm số y = 7x3+3x2+(9-3m)x+1 đồng biến trên [0;1]?
A. 5 B. 6 C. Vô số D. 3
Lời giải:
Bài 200: Gọi S là tổng tất cả giá trị nguyên của tham số m (m < 3) để bất phương trình 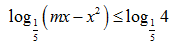
A. S = -3. B. S = -7. C. S = 0. D. S = -4.
Lời giải:
(199k) Học Toán 12 KNTTHọc Toán 12 CDHọc Toán 12 CTST
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi Tốt nghiệp THPT khác:
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 1)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 2)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 3)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản - phần 4)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao - phần 1)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao - phần 2)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao - phần 3)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao - phần 4)
- 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao - phần 5)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều



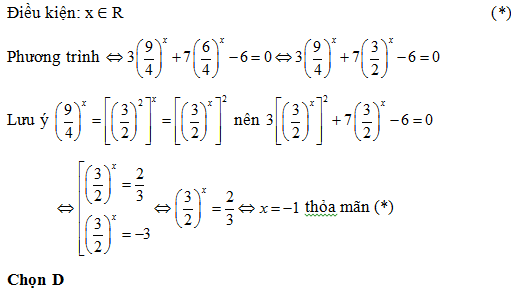
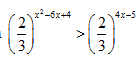
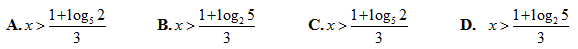
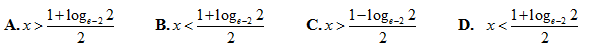

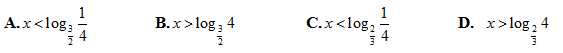

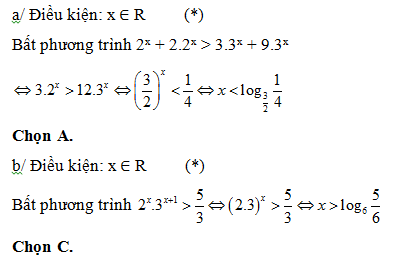
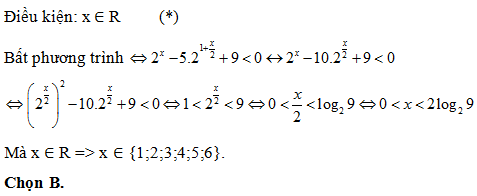
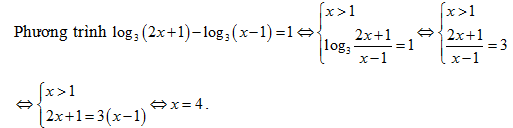
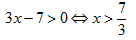
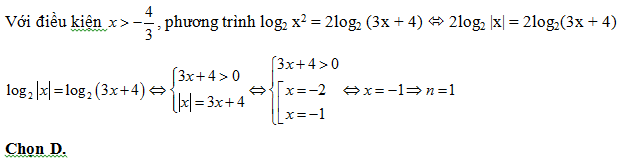
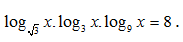
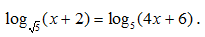
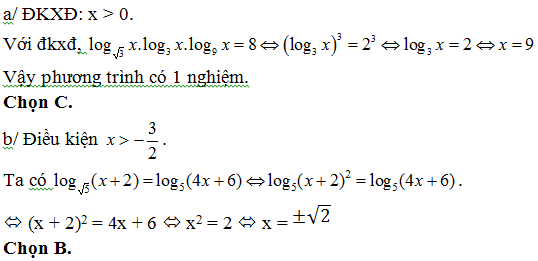
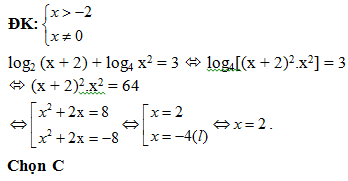
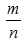

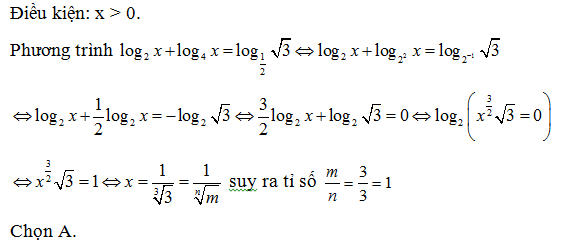
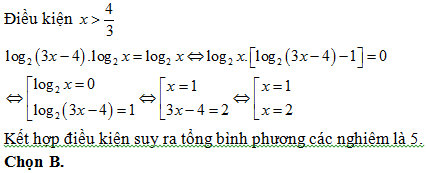
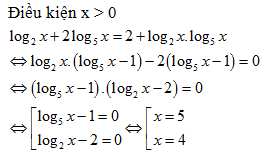
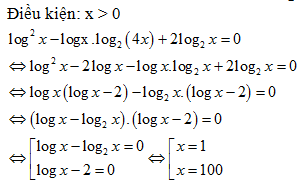
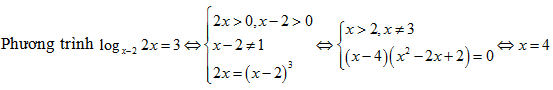
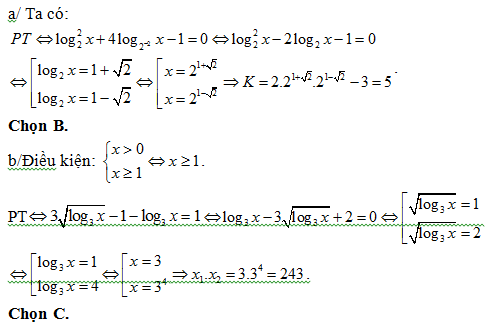
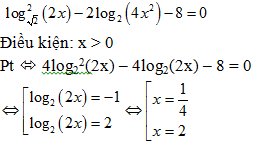
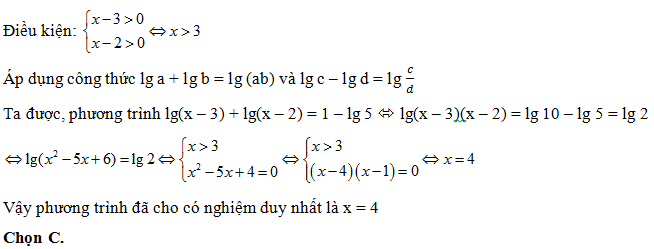

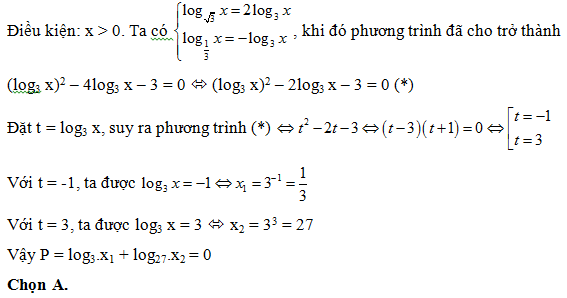
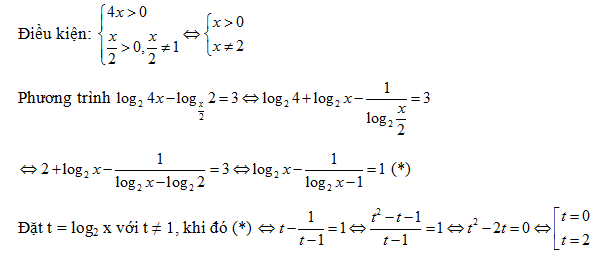
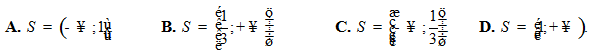
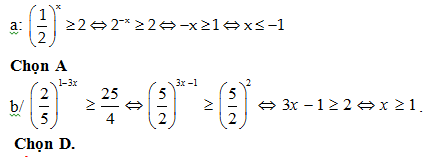

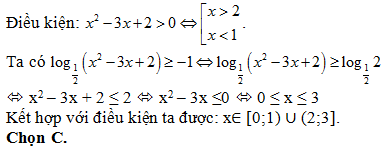
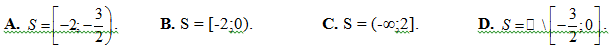
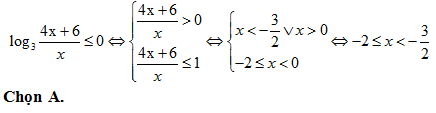
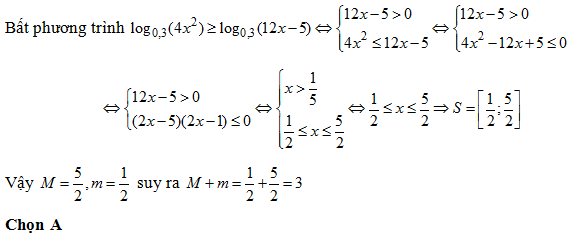
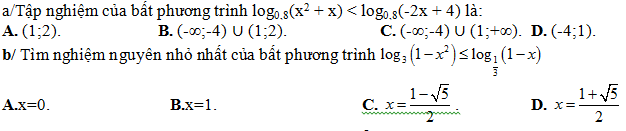
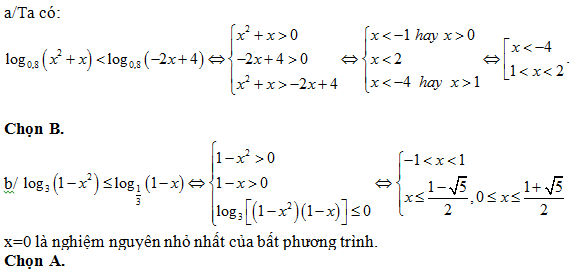
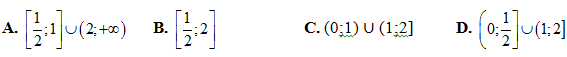


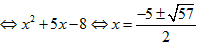
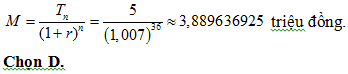
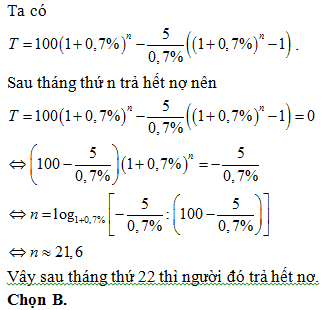
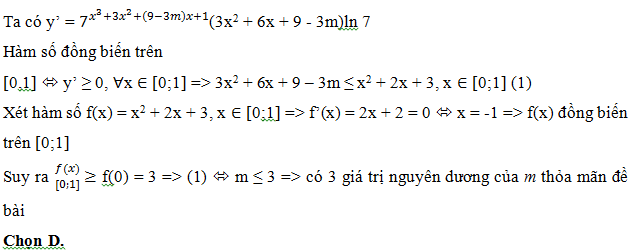
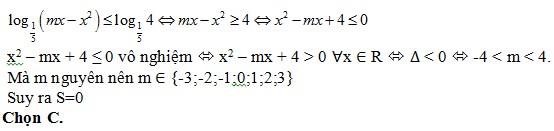



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

