200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 5)
Với 200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số (nâng cao - phần 5) có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số (nâng cao - phần 5).
200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 5)
(199k) Học Toán 12 KNTTHọc Toán 12 CDHọc Toán 12 CTST
Bài 1: Cho hàm số 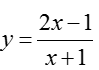
A.3e B.2e C.e D.4e
Lời giải:
+ Ta có
+ Gọi
Phương trình tiếp tuyến tại M là
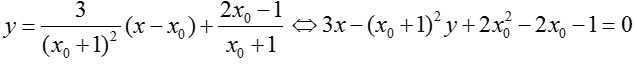
+
+ Dấu "=" xảy ra khi và chỉ khi
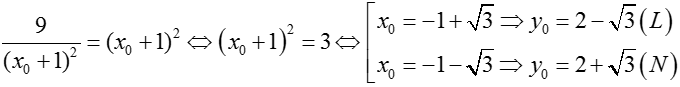
Tung độ này gần với giá trị e nhất trong các đáp án.
Chọn C.
Bài 2: Cho hàm số 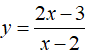
A. 7. B. 5. C. 6. D. 4.
Lời giải:
+ Gọi
Phương trình tiếp tuyến tại M có dạng
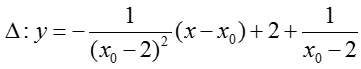
+ Giao điểm của ∆ với tiệm cận đứng là
+ Giao điểm của ∆ với tiệm cận ngang là B( 2xo-2; 2) .
+ Ta có
Dấu "=" xảy ra khi
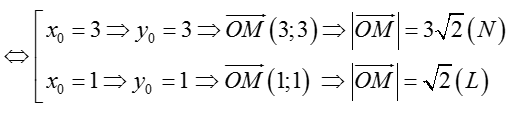
Chọn D.
Bài 3: Viết phương trình tiếp tuyến d của đồ thị (C) : 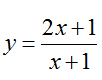
A. y = 1/4x + 1/4 , y= x+3; y= x+1 B. y = 1/4x + 5/2 , y=x+5; y= x+4
C. y = 1/4x + 5/4 , y= x+4; y=x+1 D. y = 1/4x + 5/4 , y= x+ 5, y= x+1
Lời giải:
Gọi M( xo; yo) , xo ≠ -1 là tọa độ tiếp điểm của d và (C).
Khi đó d có hệ số góc 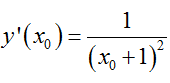
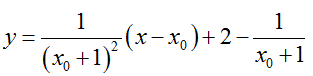
Vì d cách đều A: B nên d đi qua trung điểm I( -1; 1) của AB hoặc cùng phương với AB .
TH1: d đi qua trung điểm I( -1; 1) , thì ta luôn có:
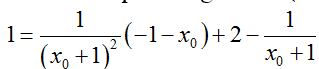
Với xo= 1 ta có phương trình tiếp tuyến d : y = 1/4x + 5/4 .
TH2: d cùng phương với AB , tức là d và AB có cùng hệ số góc, khi đó 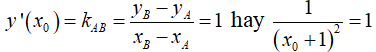
Với xo = -2 ta có phương trình tiếp tuyến d: y= x+ 5.
Với xo = 0 ta có phương trình tiếp tuyến d: y=x+ 1.
Vậy, có 3 tiếp tuyến thỏa mãn đề bài: y = 1/4x + 5/4 , y= x+ 5, y=x+ 1
Chọn D
Bài 4: Cho hàm số y= 3x-4x3 có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
A. 0. B. 3. C. 2. D. 1.
Lời giải:
+ Đường thẳng đi qua M(1;3) có hệ số góc k có dạng d: y=k(x-1)+3 .
+ d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
Thay (2) vào (1) ta được
3x-4x3 = (3-12x2)(x-1) + 3 ⇔ 8x3 - 12x2 = 0
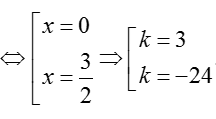
Vậy có 2 tiếp tuyến.
Chọn C.
Bài 5: Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x4 - 2x2 + 2
A.2 B.3 C.0 D.1
Lời giải:
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A∈d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
Thay (2) vào (1) ta suy ra được 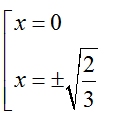
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
Bài 6: Cho hàm số y= x3-6x2+9x-1 có đồ thị là (C) . Từ một điểm bất kì trên đường thẳng x=2 kẻ được bao nhiêu tiếp tuyến đến (C) :
A.2 B. 1 C.3 D.0
Lời giải:
+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x= 2 có dạng:
∆: y= k( x-2) hay y= kx-2k
+ ∆ là tiếp tuyến của (C)
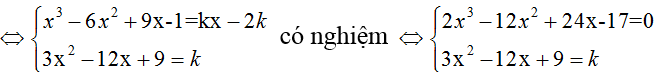
+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x=2có dạng y= a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B
Bài 7: Tìm m để từ điểm M( 1; 2) kẻ được 2 tiếp tuyến đến đồ thị (C) y= x3-2x2+(m-1) x+2m.
A. m= 10/81; m=-3 B.m=100/81; m=3 C.m=10/81; m=3 D.m=100/ 81; m=-3
Lời giải:
Gọi N( xo; yo) ∈( C). Phương trình tiếp tuyến d tại N là:
y = (3o2 - 4xo + m - 1) (x-xo) + xo3 - 2xo2 + (m-1)xo + 2m
M ≠ (d) ⇔ 2xo3 + 5xo2 - 4xo = 3 - 3m (*)
Dễ thấy (*) là phương trình hoành độ giao điểm của đồ thị y= 3-3m và f(xo) = 2xo3 + 5o2 - 4xo
Xét hàm số f(xo) = 2xo3 + 5xo2 - 4xo có f'(xo) = 6xo2 + 10xo - 4
f'(xo) = 0 ⇔ xo = -2 hoặc xo = 1/3 .
Lập bảng biến thiên, suy ra m= 100/ 81; m=-3
Chọn D.
Bài 8: Cho hàm số 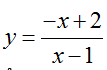
A. 1 . B. 3/2 . C. 5/2 . D. 1/2 .
Lời giải:
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là : y= k ( x-a) + 1
+ Phương trình hoành độ giao điểm của d và C :
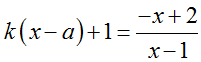
⇔ (kx-ka+1) (x-1) = -x +2 (x≠ 1)
Hay kx2+ (-k-ka+2) x-3+ka=0 ( *)
+ Với k= 0 , ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
+ Với k≠0, d và C tiếp xúc nhau khi (1) có nghiệm kép
⇔ Δx = [k(1+a)-2]2 - 4(k-3+ka) = 0
⇔ Δx = k2(1-a)2 - 4(ka-2) + 4 = 0
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1)vẽ được đúng tiếp tuyến thì phương trình ∆ =0 có đúng một nghiệm k≠0.
*Xét 1-a= 0 hay a=1, ta có 4k+4= 0 hay k= -1 thỏa mãn
*Có f(0)=4 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là 0.
*Còn lại là trường hợp Δx có nghiệm kép khi
Δ'k = 4((a-2)2 - (a-1)2) = 4(2a-3) = 0 ⇔ a = 3/2
Tổng là 1+ 3/2=5/2.
Chọn C.
Bài 9: Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2≤0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1≥0
A. m ≤ -1 . B. m ≤ -4/7 . C. m ≥ -4/7 . D. m ≥ -1 .
Lời giải:
Bất phương trình x2-3x+2≤0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1≥0
⇔ m(x2 + x + 1) ≥ -x-2
Xét hàm số 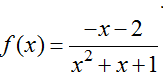
Có 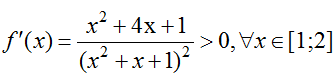
Yêu cầu bài toán
⇔ m ≥ -4/7
Chọn C.
Bài 10: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 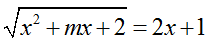
A. m ≥ -7/2 . B. m ≥ 3/2 . C. m ≥ 9/2 . D. mọi m
Lời giải:
Điều kiện: x ≥ -1/2
Phương trình
Vì x=0 không là nghiệm nên (*)
Xét 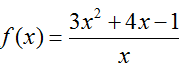
Ta có
Bảng biến thiên
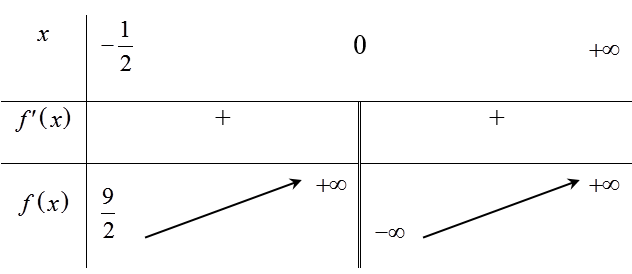
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9/2 .
Chọn C
Bài 11: Bất phương trình 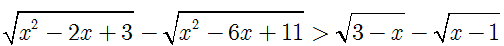
A. 1. B. 2. C. 3. D.-1
Lời giải:
Điều kiện: 1≤ x ≤ 3
bpt
Xét 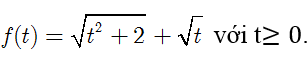
Có
Do đó hàm số đồng biến trên [0; +∞] .
Từ (1) suy ra f(x-1) > f(3-x) hay x-1 > 3-x
Suy ra : x > 2
So với điều kiện, bpt có tập nghiệm là S= (2; 3]
Do đó; a=2; b=3 và b-a=1
Chọn A.
Bài 12: Phương trình x3 + x(x+1) = m (x2+1)2 có nghiệm thực khi và chỉ khi:
A. -6 ≤ m ≤ -3/2. B. -1 ≤ m ≤ 3. C. m ≥ 3 . D. -1/4 ≤ m ≤ -3/4
Lời giải:
Ta có x3 + x(x+1) = m (x2+1)2
Xét hàm số 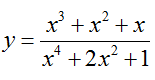
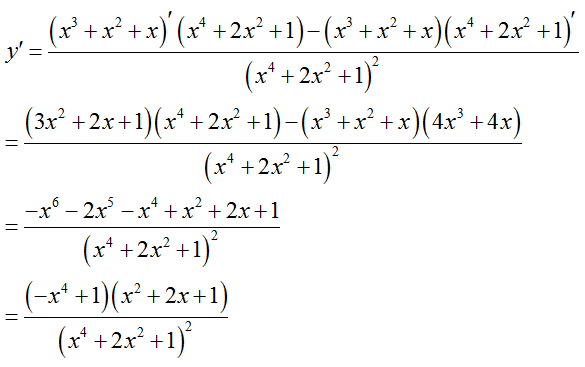
y' = 0 ⇔ (-x4+1) (x2 + 2x + 1) = 0
Bảng biến thiên
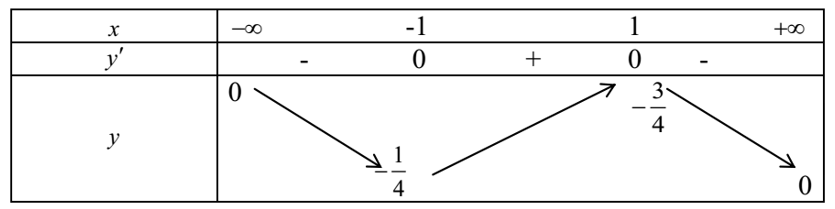
Phương trình (1) có nghiệm thực khi đường thẳng y=m cắt đồ thị hàm số
⇔ -1/4 ≤ m ≤ -3/4
Chọn D.
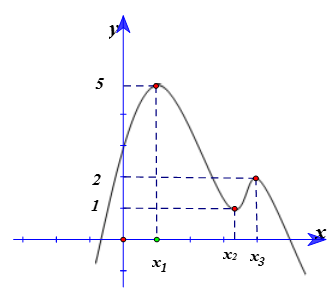
Bài 13: Cho hàm số y= f( x) ) liên tục trên R. Hàm số y= f’ (x) có đồ thị như hình vẽ. Hàm số 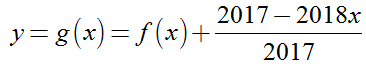
A. 1 B. 2
C. 3 D. 4
Lời giải:
Ta có y’ = g’ (x) = f’(x) -2018/2017.
Suy ra đồ thị của hàm số g’(x) là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương Oy xuống dưới 2018/2017 đơn vị.
Ta có 1 < 2018/2017 < 2 và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.
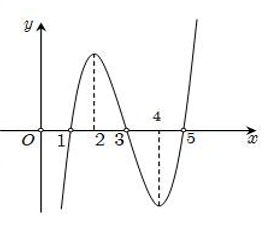
Bài 14: Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Đặt g(x) = f(x+1). Kết luận nào sau đây đúng?
A. Hàm số g(x) có hai điểm cực trị.
B. Hàm số g(x) đồng biến trên khoảng (1; 3).
C. Hàm số g(x) nghịch biến trên khoảng (2; 4) .
D. Hàm số g(x) có hai điểm cực đại và một điểm cực tiểu.
Lời giải:
g'(x) = f'(x+1) = 0
g'(x) = f'(x-1) > 0
Chọn C.
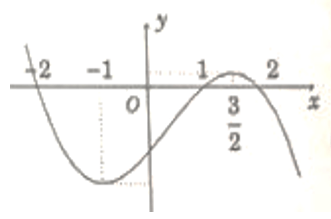
Bài 15: Cho hàm số y= f(x) có đạo hàm trên R thoả f(2) = f(-2) = 0 và đồ thị của hàm số y= f’ (x) có dạng như hình bên. Hàm số y= (f(x))2 nghịch biến trên khoảng nào trong các khoảng sau ?
A. (-1;3/2) B. (-1;1) C. (-2;-1) D. (1;2)
Lời giải:
Dựa vào đồ thị hàm số ta thấy: f’(x) = 0 khi và chỉ khi x= 1; x=±2
Ta có bảng biến thiên :
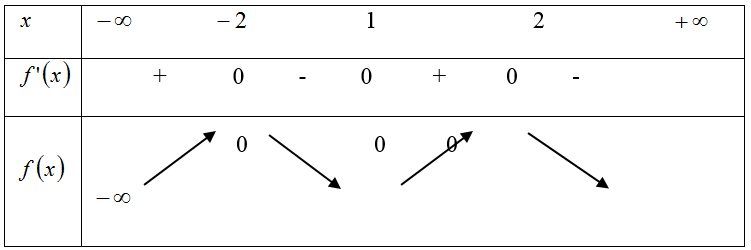
Dựa vào bảng biến thiên ta thấy f(x) < 0 với mọi x≠ ± 2
Xét hàm số y= (f(x))2 có đạo hàm y’ = 2f(x). f’ (x)
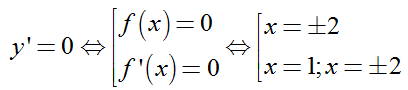
Bảng xét dấu
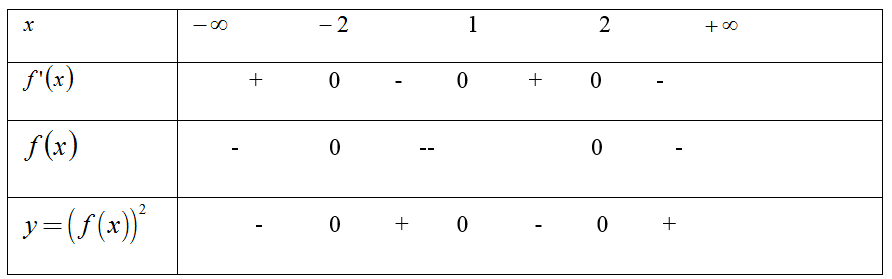
Chọn D.
Bài 16: Cho hàm số y= f( x) và đồ thị hình bên là đồ thị của hàm y= f’(x) . Hỏi đồ thị của hàm số g(x)= |2f(x)- (x-1)2| có tối đa bao nhiêu điểm cực trị ?
A. 6. B. 7. C. 8. D. 9.
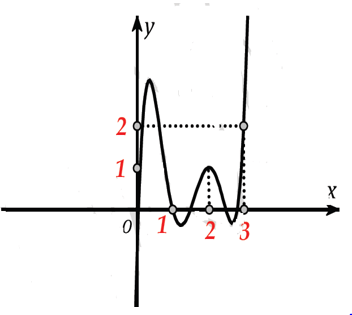
Lời giải:
Đặt h(x) = 2f(x) – ( x-1)2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
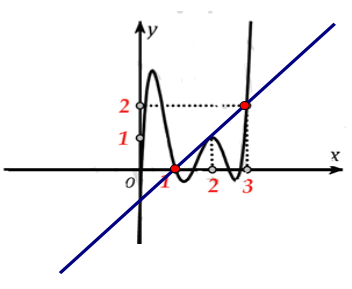
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > 0 khi f’(x) > x-1
Ta có :
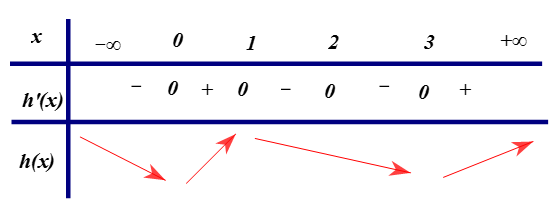
Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.
Bài 17: Cho hàm số y= f(x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương và đồ thị hàm số y= f’ ( x) cho bởi hình vẽ bên. Tìm phần nguyên của giá trị diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 2. B. 27. C. 29. D. 35.
Lời giải:
Ta có đạo hàm : f’(x) = 3ax2 + 2bx+ c.
Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số y= f’ (x) đi qua 3 điểm ( -1; 0) ; (3; 0) ; (1; -4)
Thay tọa độ 3 điểm này vào hàm f’ ta tìm được: a= 1/3; b= -1; c= -3.
Suy ra: f’ (x) = x2-2x-3 và f(x) = 1/3.x3-x2-3x+d.
Do (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương nên ta có:
F’(x) =0 khi và chỉ khi x=3 ( x= -1 bị loại vì âm)
Như vậy (C) đi qua điểm (3; -9) ta tìm được d=0.
Vậy hàm số đề bài cho là f(x) = 1/3.3-x2-3x.
Xét phương trình trình hoành độ giao điểm và trục hoành:
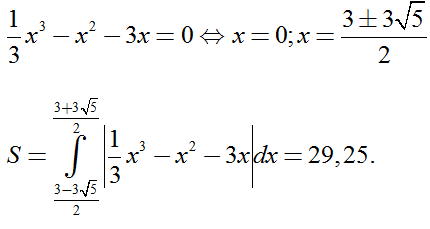
Chọn C.
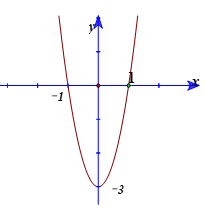
Bài 18: Cho hàm số y= f(x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
A. y =x3-3x+2. B. y =x3+3x+2. C y= x3-2x+2. D. y = x3-3x-1.
Lời giải:
+ Ta có đạo hàm : f’(x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3b và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:
f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2
Khi đó; f( x) = x3-3x+2.
Chọn A.
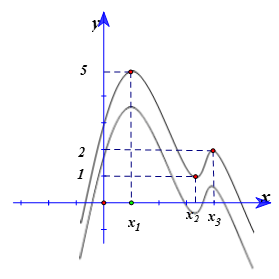
Bài 19: Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y= f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ?
A.24. B. 28. C. 26. D. 21.
Lời giải:
Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2 + 2 và f( x) = x3+ 2x+ d
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0 = 0 + 0 + d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) – f(2) =21
Chọn D.
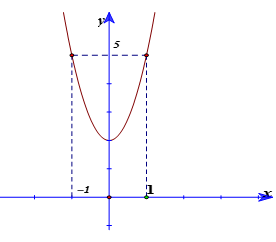
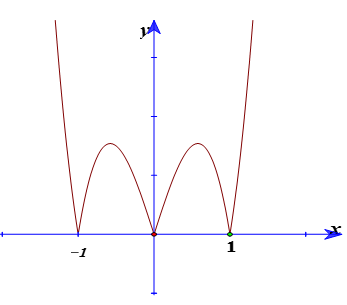
Bài 20: Cho hàm số y= f(x) = ax4+ bx2 + c ( a > 0) có đồ thị (C), đồ thị hàm số y = |f'(x)| như hình vẽ. Biết đồ thị hàm số y= f’(x) đạt cực tiểu tại điểm (√3/3; -8√3/9) . Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7/15 B. 8/15 C. 14/15 D. 16/15
Lời giải:
+ Từ đồ thị của hàm số y = |f'(x)|và a > 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua (1;0); (√3/3; -8√3/9) ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) = x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
4-2x2+1 = 0 nên x=± 1
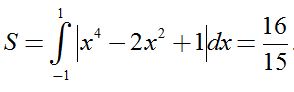
Chọn D.
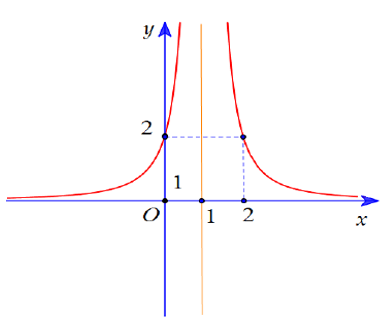
Bài 21: Cho hàm số 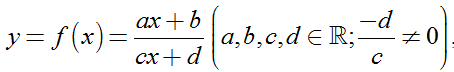
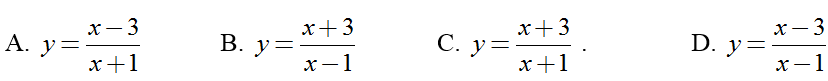
Lời giải:
+ Ta có 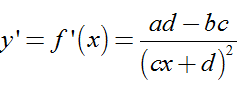
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x) đi qua điểm (2;2)
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
Chọn D.
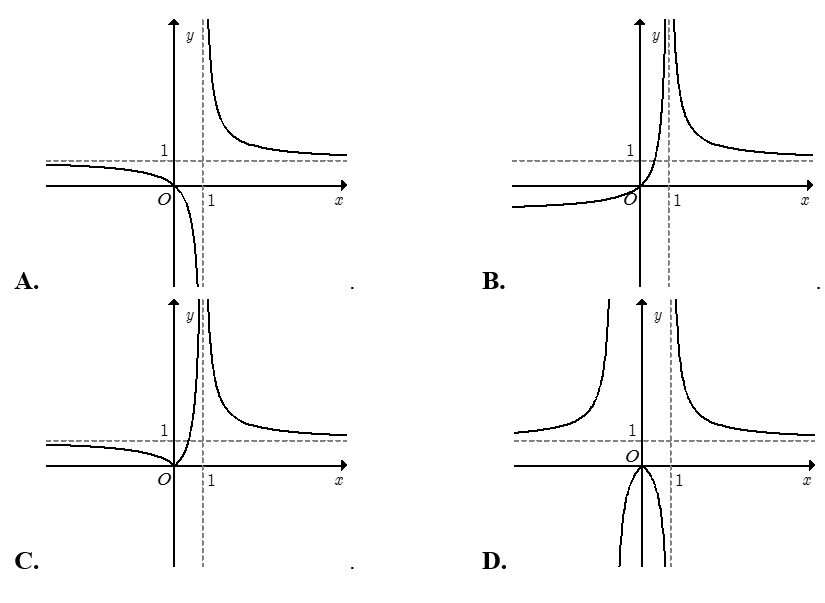
Bài 22: Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số y= x/|x-1| ?
Lời giải:
Ta có
Do đó đồ thị hàm số y= x/|x-1| được suy từ đồ thị hàm số y = x/(x-1) bằng cách:
● Giữ nguyên phần đồ thị hàm số phía bên phải đường thẳng x=1
● Phần đồ thị hàm số y= x/(x-1) phía bên trái đường thẳng x = 1 thì lấy đối xứng qua trục hoành.
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số y= x/|x-1| .
Chọn B.
Bài 23: Hàm số y= 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình 2|x|3-9x2+12|x|+m = 0 có sáu nghiệm phân biệt.
A. m < - 5 B. -5 < m < - 4 C. 4 < m < 5 D.m > -4
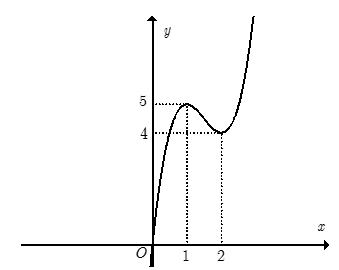
Lời giải:
+ Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x, ta suy ra đồ thị hàm số y=2|x|3-9x2+12|x| như hình dưới đây:
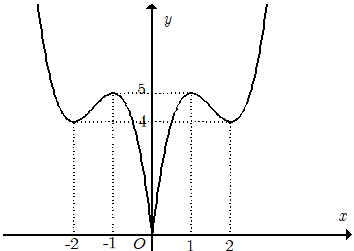
+ Phương trình 2|x|3- 9x2+12|x|+m = 0 tương đương
2|x|3- 9x2+12|x|= -m là phương trình hoành độ giao điểm của đồ thị hàm số
y = 2|x|3- 9x2+12|x| và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y =2|x|3- 9x2+12|x|, yêu cầu bài toán trở thành:
4 < -m < 5 hay -5 < m < -4.
Chọn B.
Bài 24: Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)|=m có đúng hai nghiệm phân biệt.
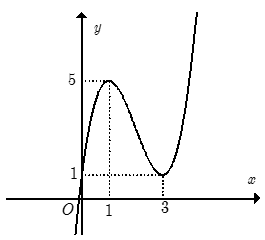
A.0 < m < 1 . B. m > 5. C.m= 1; m= 5 D.0 < m < 1; m > 5
Lời giải:
+ Ta có
Từ đó suy ra cách vẽ đồ thị hàm số ( C) từ đồ thị hàm số y= |f(x)|như sau:
- Giữ nguyên đồ thị y= f (x) phía trên trục hoành.
- Lấy đối xứng phần đồ thị y= f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
Kết hợp hai phần ta được đồ thị hàm số y= |f(x)| như hình vẽ.
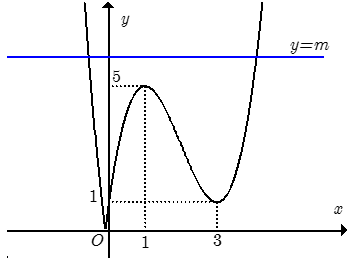
Phương trình |f(x)| = m là phương trình hoành độ giao điểm của đồ thị hàm số y= |f(x)| và đường thẳng y= m (cùng phương với trục hoành).
Dựa vào đồ thị, ta có ycbt
Chọn D.
Bài 25: Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình 2|f(x)|-m=0 có đúng bốn nghiệm phân biệt.
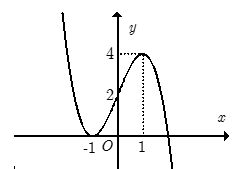
A. 0 < m < 8. B.m > 4. C.m < 0 ; m > 8 D. -2 < m < 4
Lời giải:
+ Trước tiên từ đồ thị hàm số y= f( x), ta suy ra đồ thị hàm số y= |f(x)| như hình dưới đây:
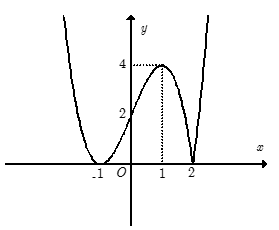
Phương trình 2|f(x)|-m=0 hay |f(x)|= m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y= |f(x)| và đường thẳng y= m/2
Dựa vào đồ thị hàm số y= |f(x)|, ta có ycbt trở thành: 0 < m/2 < 4 hay 0 < m < 8
Chọn A.
Bài 26: Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|)=-1/2 có bao nhiêu nghiệm?
A. 2 . B. 0 . C. 6 . D. 4
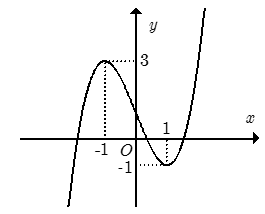
Lời giải:
+ Trước tiên tịnh tiến đồ thị sang phải 2 đơn vị để được đồ thị hàm số y= f(x-2) .
Tiếp theo giữ phần đồ thị phía bên phải đường thẳng x= 2, xóa bỏ phần đồ thị phía bên trái đường thẳng x= 2.
Cuối cùng lấy đối xứng phần đồ thị vừa giữ lại ở trên qua đường thẳng x= 2. Ta được toàn bộ phần đồ thị của hàm số y= f(|x-2|) (hĩnh vẽ bên dưới)
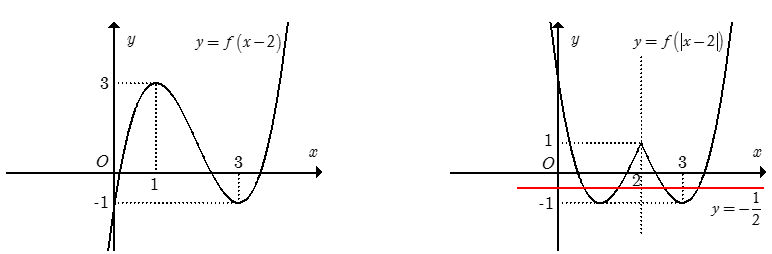
Dựa vào đồ thị hàm số y= f(|x-2|), ta thấy đường thẳng y= -1/2 cắt đồ thị hàm số y= f(|x-2|) tại 4 điểm phân biệt khi và chỉ khi phương trình f(|x-2|)=-1/2 có 4 nghiệm phân biệt.
Chọn D.
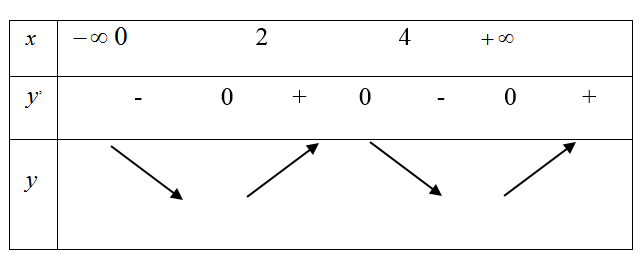
Bài 27: Cho hàm số y= f(x)= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
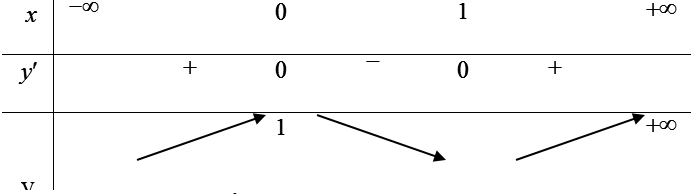
Khi đó |f(x)|=m có bốn nghiệm phân biệt x1 < x2 < x3 < 1/2 < x4 khi và chỉ khi
A. 1/2 < m < 1 B. 0 < m C.m > 1 D.m < 1/2
Lời giải:
Ta có 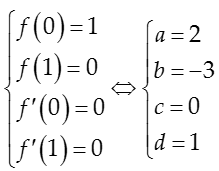
Ta thấy:
Bảng biến thiên của hàm số y=|f(x)| như sau:
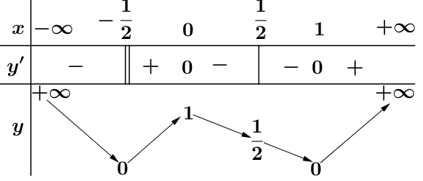
Dựa vào bảng biến thiên suy ra phương trình |f(x)|=m có bốn nghiệm phân biệt x1 < x2 < x3 < 1/2 < x4 khi và chỉ khi 1/2 < m < 1.
Chọn A.
Bài 28: Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình |x|3-3x2+2=m có nhiều nghiệm thực nhất
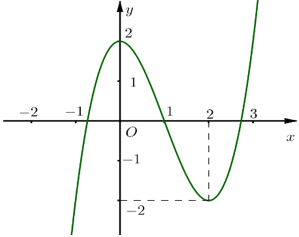
A.m > -2. B.m > 0.
C.-2 < m < 2. D.m < 2
Lời giải:
+ Ta có hàm số g(x)= |x|3-3x2+2 là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.
+ Khi x≥ 0 ; g(x) = x3-3x2+ 2
Do đó; đồ thị hàm số g(x)= |x|3-3x2+2 có dạng như hình vẽ.
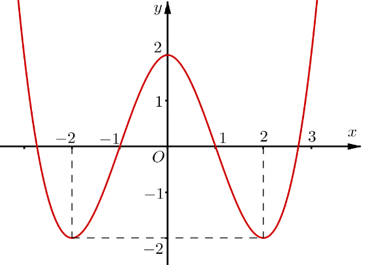
+ Dựa vào đồ thị suy ra phương trình |x|3-3x2+2=m có nhiều nghiệm thực nhất khi và chỉ khi -2 < m < 2.
Chọn C.
Bài 29: Hình vẽ bên là đồ thị của hàm số y= x3-3x-1. Tất cả các giá trị thực của để phương trình |x33-3x-1| = m có 3 nghiệm đôi một khác nhau là
A.m= 1 B.m > 1. C.3 < m. D.m= 0 hoặc m= 3
Lời giải:
+ Cách vẽ đồ thị hàm số y= |x3-3x-1| từ đồ thị hàm số y= x3-3x-1 (C) .
+ Giữ nguyên phần đồ thị (C) phía trên trục hoành.
+ Lấy đối xứng phần đồ thị (C) phía dưới trục hoành qua trục hoành và bỏ phần đồ thị phía dưới trụ hoành.
+ Hợp hai phần đồ thị trên ta được đồ thị hàm số y= |x3-3x-1| (như hình vẽ).
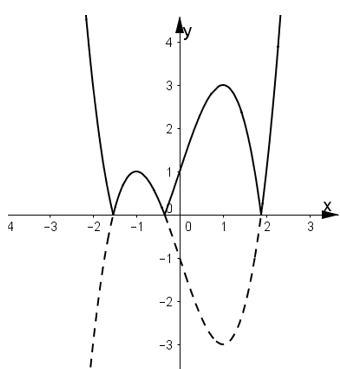
+ Để phương trình |x3-3x-1| = m có 3 nghiệm đôi một khác nhau thì đường thẳng y= m cắt đồ thị hàm số y= |x3-3x-1| tại 3 điểm phân biệt
Chọn D.
Bài 30: Tìm tất cả các giá trị thực k đề phương trình 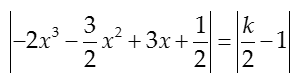
A. k > 6 B. 1 < k < 2
C. -2 < k < 6 D. k ∈ (-2;-3/4) ∪ (19/4;6)
Lời giải:
+ Đặt f(x)= -2x3-3/2 x2+3x+1/2
+ Đạo hàm f’(x) = -6x2-3x+ 3 và f’(x) = 0 khi x= -1 hoặc x= 1/2
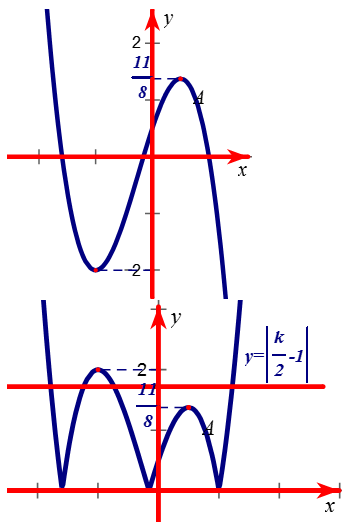
BBT
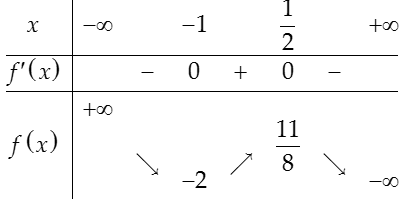
+ Suy ra đồ thị của hàm trị tuyệt đối y= 3|-2x3-3/2 x2+3x+1/2| bằng cách lấy đối xứng qua trục Ox
Vậy để PT có đúng 4 nghiệm phân biệt ⇔ 11/8 < |k/2-1| < 2 ⇔ 121/64 < k2/4 - k + 1 < 4
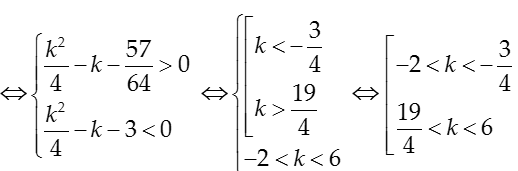
Chọn D
Bài 31: Cho hàm số 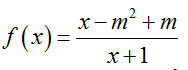
A. m= 1 B. m= -2 C. m= -1 D. m= -1 hoặc m= 2
Lời giải:
Đạo hàm
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
Bài 32: Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y= |x2-2x+m| trên đoạn [-1; 2] bằng 5.
A. -4 B. 2 C. 0 D . -2
Lời giải:
+ Xét hàm số f(x) = x2- 2x trên đoạn [ -1; 2]
+ Ta có đạo hàm f’(x) = 2( x-1) và f’(x) =0 khi x= 1 .
Vậy:
TH1. Với 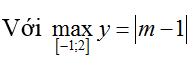
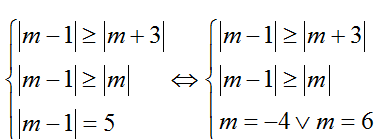
TH2. Với 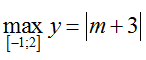
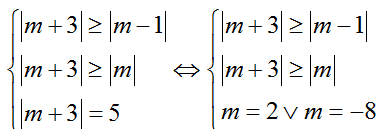
TH3. Với 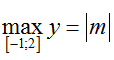
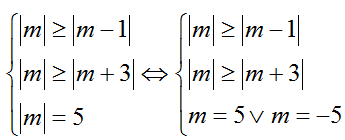
Chọn D.
Bài 33: Cho hàm số 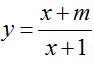
A .m=0 B.m= 2 C.m= 4 D.m= 5
Lời giải:
+ Đạo hàm
+ Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m≠ 1.
+ Khi đó ta có :
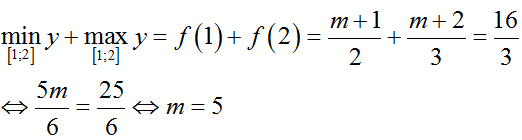
Chọn D.
Bài 34: Cho hàm số 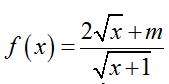
A.1 < m < 3 B. m ∈ (1;3√5-4) C. m (∈ 1;√5) D.1 < m≤ 4
Lời giải:
+ Đạo hàm
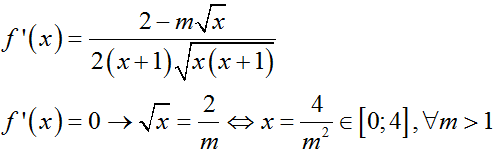
+ Lập bảng biến thiên, ta kết luận được
+ Vậy ta cần có 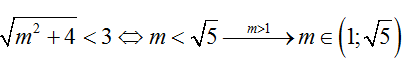
Chọn C.
Bài 35: Cho hàm số y= x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m > 0 , để giá trị nhỏ nhất của hàm số trên D= [m+ 1; m+ 2] luôn bé hơn 3 là:
A. (0; 1) B ( 1/2; 1) C. (2; 3) D. (0; 2)
Lời giải:
+ Ta có đạo hàm : y= 3x2- 3 và y’ =0 khi và chỉ khi x= 1 hoặc x= -1 .
+ Hàm số đồng biến trên khoảng ( 1; + ∞) .
+ Trên D= [m+1; m+ 2], với m > 0 , ta có :
Ycbt min y < 3 hay m3+ 3m2-4 < 0
Suy ra ( m-1) (m+ 2)2) < 0
Khi đó: m < 1 và m≠- 2
+ Kết hợp điều kiện . Suy ra: 0 < m < 1.
Chọn A.
Bài 36: Cho hàm số: y= (x+m)/(x-1), với tham số m bằng bao nhiêu thì
A.m= 1 B. m= 3 C.m= 5 D. m= -1
Lời giải:
+ Đạo hàm
TH1. Với m > -1 suy ra f’(x) < 0 mọi x≠ 1 nên hàm số f(x) nghịch biến trên mỗi khoảng xác định.
Khi đó
TH2. Với m < -1 suy ra f”(x) > 0 mọi x≠1 nên hàm số f(x) đồng biến trên mỗi khoảng xác định.
Khi đó
Chọn C.
Bài 37: Tìm tất cả các giá trị thực của tham số m để hàm số 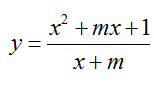
A. 0 < m < 1 B. m < 0 C. m > 1 D. -1 < m < 0
Lời giải:
Điều kiện : x≠ -m.
+ Ta có:
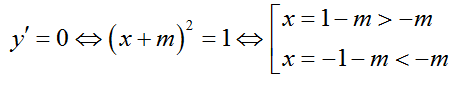
+ Do hệ số x2 là số dương và theo yêu cầu đề bài ta có bảng biến thiên như sau:

+ Hàm số đạt giá trị nhỏ nhất tại xo=1-m∈(0;2) nên 0 < -m+1 < 2
Hay -1 < m < 1.
+ Kết hợp điều kiện để hàm số liên tục trên [0; 2] thì
Ta được 0 < m < 1.
Chọn A.
Bài 38: Tìm m để bất phương trình x2-5mx+9 ≥0có nghiệm x∈[1;9]?
A.m≤ 2 B.m≤ 1 C. m≥ 2 D. Đáp án khác
Lời giải:
+ Với x∈[1;9] pt
Xét 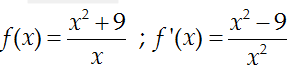
+ Suy ra
Ycbt
Chọn A.
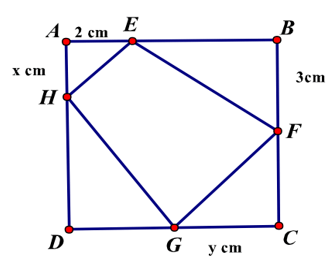
Bài 39: Cho một tấm nhốm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y để dịnh tích hình thang EFGH đạt giá trị nhỏ nhất.
A.2+ √3 B. 3√2 C. 2√2 D. Tất cả sai
Lời giải:
Ta có SEFGH nhỏ nhất ⇔ S = SAEH + SCGF + SDGH lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên AE/CG = AH/CF => xy = 6 (2)
Từ (1) và (2) suy ra 2S= 42-( 4x - 18/x).
Ta có 2S nhỏ nhất khi và chỉ khi 4x- 18/x nhỏ nhất.
Biểu thức 4x- 18/x nhỏ nhất ⇔ 4x = 18/x ⇔ x = 3√2/2 => y = 2√2
Vậy x + y = 3√2/2 + 2√2
Chọn D.
Bài 40: Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn là để ít tốn vật liệu nhất. Gần với giá trị nào nhất
A. 10, 5 B. 10,6 C. 10, 7 D. 10, 8
Lời giải:
Để ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất.
Tức là Stp= 2πR2+ 2πRh nhỏ nhất ( với R là bán kính đường tròn đáy)
Thể tích bồn nước V = πR2h = 1000
Khi đó
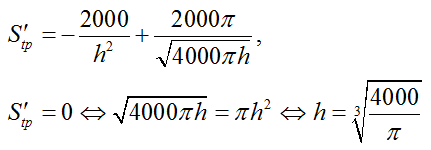
Sử dụng bảng biến thiên, ta tìm được Stp nhỏ nhất khi
Chọn D.
(199k) Học Toán 12 KNTTHọc Toán 12 CDHọc Toán 12 CTST
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi Tốt nghiệp THPT khác:
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 1)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 2)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 3)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 4)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 5)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 6)
- 275 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (cơ bản - phần 7)
- 200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 1)
- 200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 2)
- 200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 3)
- 200 bài tập trắc nghiệm Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số có lời giải (nâng cao - phần 4)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

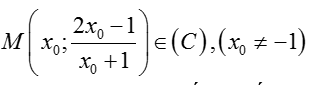
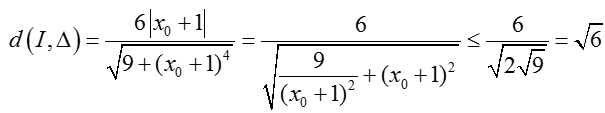
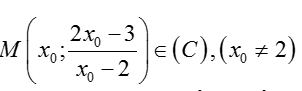
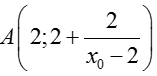
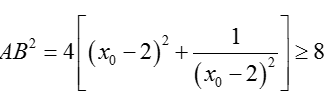
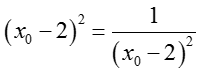
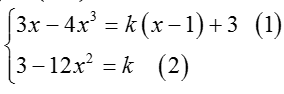
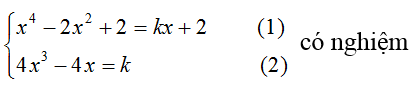
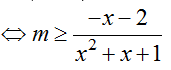
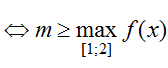
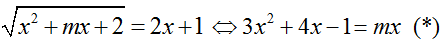
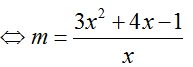
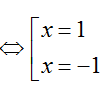
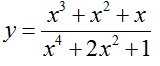
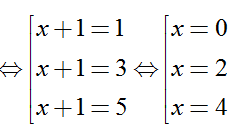
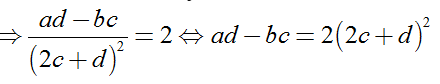
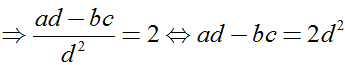
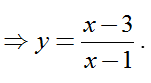
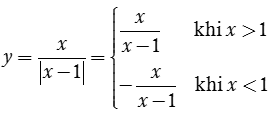
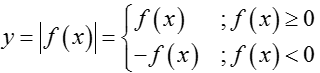
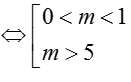
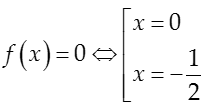
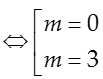
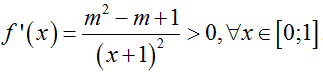
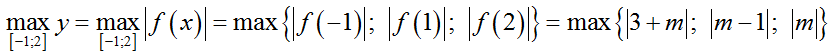
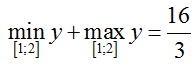
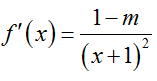
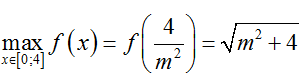
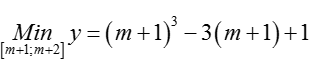
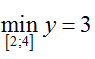
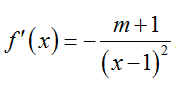
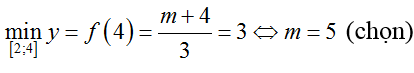
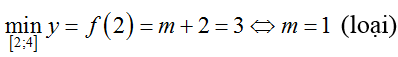
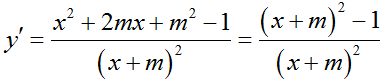
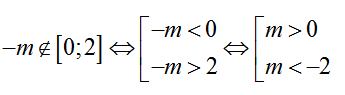
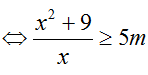
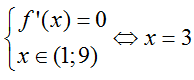
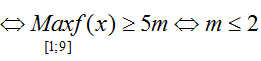
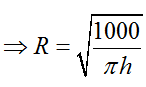
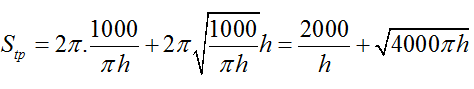
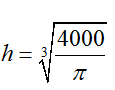



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

