Đề thi Giữa kì 1 Toán 10 năm 2023-2024 trường THPT Quế Sơn (Quảng Nam)

Với đề thi Giữa kì 1 Toán 10 năm 2023-2024 trường THPT Quế Sơn (Quảng Nam) có đáp án sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 10.

Đề thi Giữa kì 1 Toán 10 năm 2023-2024 trường THPT Quế Sơn (Quảng Nam)

Xem thử Đề GK1 Toán 10 KNTT Xem thử Đề GK1 Toán 10 CTST Xem thử Đề GK1 Toán 10 CD

Chỉ từ 200k mua trọn bộ Đề thi Giữa kì 1 Toán 10 (mỗi bộ sách) theo cấu trúc mới bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1 trường THPT Quế Sơn (Quảng Nam)

Năm học 2023-2024

Môn: Toán 10

Thời gian làm bài: phút

(Đề 101)

A.  TRẮC NGHIỆM ( 15 câu x 1/3 = 5,0 điểm).

            Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.

Câu 1:  Trong các câu sau, câu nào là mệnh đề ?    

A.  Hãy làm bài kiểm tra giữa học kỳ 1 thật nghiêm túc!            

B.  $x^2-7>3x$       

C.  Em có thích học môn Toán không?                                         

D.  Số 2023 là số chẵn.                

Câu 2: Mệnh đề phủ định của mệnh đề  “$\exists$x$\in$ N: x² + 5x – 2 > 0’’là:

 A.$\forall$x $\in$ N: x² + 5x – 2< 0.                               

B.$\exists$x$\in$ N: x² + 5x – 2< 0.     

C.$\exists$x$\in$ N: x² + 5x – 2$\le$ 0.  

D.$\forall$x $\in$ N: x² + 5x – 2 $\le$ 0.

Câu 3: Cho  M = $\left\{1,2,3,\text{ 4, }5,6,\text{ 7},8\right\}$,  N = $\left\{2,4,6,8,10\right\}$. Tập M\ N là?

A. M \ N = $\left\{1,2,4,5\right\}$.        

B. M \ N = $\varnothing$ .      

C. M \ N = $\left\{1,\text{ 3},\text{ 5},\text{ 7}\right\}$.    

D. M \ N = $\left\{1,3,5,7,8\right\}$.

Câu 4: Số tập con của $M=\left\{a,b,1\right\}$ là:    

A. 8.                                      

B. 9.

C. 7.                                    

D. 6.

Câu 5: Tập hợp M = $\left\{x \in R| 2\le x< 8\right\}$ được viết lại:

A. M = (2;8).                     

B. M = [2;8).      

C. M = [2;8].                     

D. M = (2;8].

Câu 6: Bất phương trình nào sau đây là bất phương trình bậc nhất 2 ẩn?

A. $2x.y-5y\ge 1$

B. $5x^2-2y\ge 3$

C. $5^2.x-2y\ge 3$

D. $3x-y^2\ge -5$

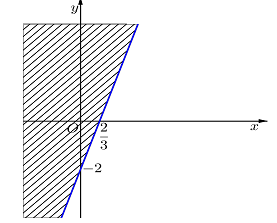
Câu 7: Hình vẽ bên, miền không bị gạch bỏ biểu diễn miền nghiệm của bất phương trình nào?

A. $-3x+y+2\ge 0$

B. $-3x+y+2\le 0$

C. $3x+y-2\ge 0$

D. $3x-y-2\le 0$

Câu 8: Cho hệ bất phương trình bậc nhất 2 ẩn: $\left\{\begin{array}{l}x-y<-3\\ x+2y\ge -4\end{array}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. O(0 ;0) .                         

B. M(3; –1).        

C. N(–2 ;1).

D. P(–3 ;1).                                       

Câu 9: Cho góc $\alpha$( 0⁰ <$\alpha$< 180⁰) , chọn phát biểu đúng.

A.  sin(180⁰ – $\alpha$) =  sin$\alpha$.           

B. cos(180⁰ –$\alpha$) = – sin$\alpha$.                                                                 

C.  cos (180⁰ –$\alpha$) =  cos$\alpha$.          

D. sin(180⁰ – $\alpha$) = – cos$\alpha$.                                                                                                        

Câu 10: Cho góc $\alpha$ với ${90}^0<\alpha <{180}^0$ Khẳng định nào sau đây là đúng?

A. $\sin \alpha <0$

B. $\cos \alpha >0$

C. $\tan \alpha <0$

D. $\cot \alpha >0$

Câu 11: Cho tanx = 3. Tính giá trị của biểu thức $M=\frac{5\sin x-\cos x}{2\sin x+\cos x}$

A. M = 1.                  

B. M = 2.                     

C. M = 3.                           

D. M = 4.                                       

Câu 12: Trong tam giác ABC, phát biểu nào sau đây đúng?

A.  a² = b² + c² – 2bc.sinA .   

B. a² = b² – c² – 2bc.cosA .

C.  a² = b² + c² – 2bc.cosA .                              

D. a² = b² +c² + 2bc.cosA.  

Câu 13: Cho tam giác ABC có a = 8; b = 7; c = 6. Số đo góc $\hat{A}$ là:

A. $\widehat{\text{A}}\approx {60}^0{37}^{\text{'}}$

B. $\hat{A}\approx {74}^0{48}^{\text{'}}16"$

C. $\widehat{\text{A}} \approx {78}^0{35}^{\text{'}}5"$

D. $\hat{A} \approx {75}^0{31}^{\text{'}}$

Câu 14: Cho tam giác ABC có $\hat{A}$= 35⁰; c = 8; $\hat{B}$=100⁰. Bán kính đường tròn ngoại tiếp R của tam giác ABC bằng:

A. R = 8$\sqrt{2}$. 

B. R = 4$\sqrt{2}$.

C. R= 3$\sqrt{2}$.

D. R= 2$\sqrt{2}$.

Câu 15: Cho tam giác ABC có a = 8 ;$\hat{C}$= 150⁰ ; b = 12. Diện tích S của tam giác ABC là:

A. S = 24.                   

B. S = 48.                

C. S = 48.

D. S = 24$\sqrt{3}$.

B. TỰ LUẬN (5, 0 điểm)

Bài 1.(1,0 điểm) Cho mệnh đề: “ Với x là số tự nhiên, nếu x chia hết cho 9 thì x chia hết cho 3.

Lập mệnh đề đảo của mệnh đề trên. Mệnh đề đảo đó đúng hay sai? Giải thích.

Bài 2.(1,0 điểm) Cho 2 tập hợp M = [– 5; 3);  N = (–3; 8]. Xác định các tập hợp M $\cap$N, M$\cup$N.

Bài 3. (1,0 điểm) Cho sin$\alpha$=$\frac{3}{5}$ với 90⁰ <$\alpha$< 180⁰. Tính các giá trị lượng giác còn lại của góc $\alpha$.

Bài 4.(1,0 điểm) Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 120^0. Tàu thứ nhất chạy với vận tốc 50km/h, tàu thứ hai chạy với vận tốc 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

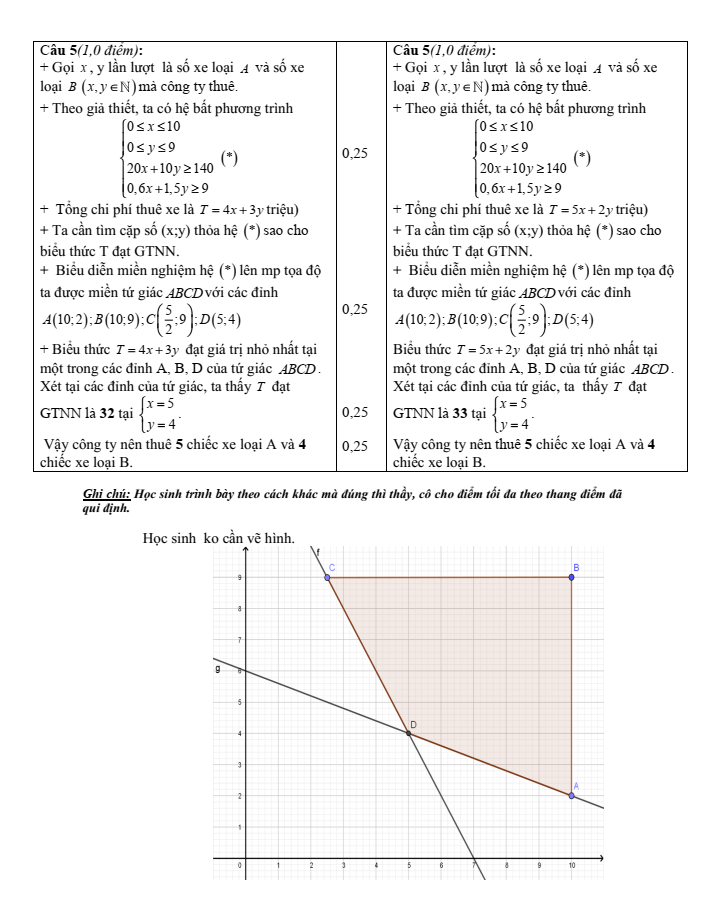
Bài 5.(1,0 điểm) Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (1 sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Biết rằng xe A chỉ chở tối đa 20người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1 trường THPT Quế Sơn (Quảng Nam)

Năm học 2023-2024

Môn: Toán 10

Thời gian làm bài: phút

(Đề 102)

A.  TRẮC NGHIỆM ( 15 câu x 1/3 = 5,0 điểm).

      Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.

Câu 1:  Trong các câu sau, câu nào không là mệnh đề ?

A.  Hà Nội là thủ đô của Việt Nam.

B.  15 chia hết cho 3.

C.  Bạn học lớp mấy?

D.  Số 2023 là số chẵn.

Câu 2: Mệnh đề phủ định của mệnh đề  “$\forall$x$\in$ N: x² + 5x – 2 < 0’’là:

 A.$\forall$x $\in$ N: x² + 5x – 2 > 0.                              

B.$\exists$x$\in$ N: x² + 5x – 2 > 0.     

C.$\exists$x$\in$ N: x² + 5x – 2$\ge$ 0.     

D.$\forall$x $\in$ N: x² + 5x – 2$\ge$ 0.

Câu 3: Cho  M = $\left\{1,2,3,\text{ 4, }5,6,\text{ 7},8\right\}$,  N = $\left\{2,4,6,8,10\right\}$. Tập M\ N là?

A. M \ N = $\left\{1,2,4,5\right\}$.        

B. M \ N = $\varnothing$ .      

C. M \ N = $\left\{1,\text{ 3},\text{ 5},\text{ 7}\right\}$.    

D. M \ N = $\left\{1,3,5,7,8\right\}$.

Câu 4: Số tập con của $M=\left\{1,2,x\right\}$ là:    

A. 7.

B. 9.

C. 6.

D. 8.

Câu 5: Tập hợp M = $\left\{x\in ℝ|1<x\le 6\right\}$được viết lại:

A. M = (1;6).

B. M = [1;6).

C. M = [1;6] 

D. M = (1;6].

Câu 6: Bất phương trình nào sau đây là bất phương trình bậc nhất 2 ẩn?

A. $3x.y-2y\le 4$

B. $5x-2^2.y\ge 1$

C. $5.x^2-2y\ge 3$

D. $3x-2y^2\ge -1$

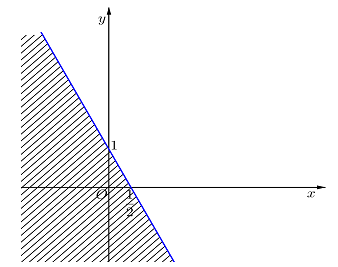
Câu 7: Hình vẽ bên, miền không bị gạch bỏ biểu diễn miền nghiệm của bất phương trình nào?

A. $2x+y\ge 1$

B. $2x+y\le 1$

C. $2x-y\ge 1$

D. $2x-y\ge -1$

Câu 8: Cho hệ bất phương trình bậc nhất 2 ẩn: $\left\{\begin{array}{l}x-y<-3\\ x+2y\ge -4\end{array}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. O(0 ;2).

B. M(3; 7).

C. N(–1 ;1).

D. P(–3 ;0).

Câu 9: Cho góc $\alpha$( 0⁰ <$\alpha$< 180⁰) , chọn phát biểu đúng.

A.  sin(180⁰ – $\alpha$) = – sin$\alpha$.         

B. cos(180⁰ –$\alpha$) = – cos$\alpha$.                                                                 

C.  cos(180⁰ –$\alpha$) =  cos$\alpha$                                        

D. sin(180⁰ – $\alpha$) = cos$\alpha$.                                                                                                                                                                                                                                       

Câu 10: Cho góc $\alpha$ với ${90}^0<\alpha <{180}^0$. Khẳng định nào sau đây là đúng?

A. $\sin \alpha <0$

B. $\cos \alpha >0$

C. $\tan \alpha >0$

D. $\cot \alpha <0$

Câu 11: Cho tanx = – 3. Tính giá trị của biểu thức $M=\frac{2\sin x+9\cos x}{\sin x+4\cos x}$

A. M = 1.

B. M = 2.

C. M = 3.

D. M = 4. 

Câu 12: Trong tam giác ABC, gọi p, R, r, S lần lượt là nửa chu vi, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp và diện tích của tam giác ABC, khẳng định nào sau đây sai?

A.  S = $2.a.b.\sin C$.   

B. S = $\frac{a.b.c}{4R}$.

C. $\frac{b}{2\sin B}=R$.                    

D. S = p. r. 

Câu 13: Cho tam giác ABC có a = 6; b = 7; c = 8. Số đo góc $\hat{C}$ là:

A. $\widehat{C}\approx {60}^0{37}^{\text{'}}$

B. $\hat{C} \approx {74}^0{48}^{\text{'}}16"$

C. $\hat{C} \approx {75}^0{31}^{\text{'}}$

D. $\hat{C} \approx {78}^0{35}^{\text{'}}5"$

Câu 14: Cho tam giác ABC có $\hat{A}$= 20⁰; c = 6; $\hat{B}$=100⁰. Bán kính đường tròn ngoại tiếp R của tam giác ABC bằng:

A. R = 4$\sqrt{3}$.

B. R = 4$\sqrt{2}$.

C. R= 2$\sqrt{3}$.

D. R= 3$\sqrt{2}$.

Câu 15: Cho tam giác ABC có a = 8 ;$\hat{C}$= 150⁰ ; b = 6. Diện tích S của tam giác ABC là:

A.   S = 24.              

B. S = 12$\sqrt{3}$.

C.  S = 24$\sqrt{3}$.

D. S = 12.

B. TỰ LUẬN (5, 0 điểm)

Bài 1.(1,0 điểm)  Cho mệnh đề: “ Với x là số tự nhiên, nếu x chia hết cho 6 thì x chia hết cho 2.

Lập mệnh đề đảo của mệnh đề trên. Mệnh đề đảo đó đúng hay sai? Giải thích.

Bài 2.(1,0 điểm)  Cho 2 tập hợp M = (– 1; 5];  N = [–3; 1). Xác định các tập hợp M$\cap$N, M$\cup$N.

Bài 3.(1,0 điểm) Cho sin$\alpha$= $\frac{4}{5}$ với 90⁰ <$\alpha$< 180⁰. Tính các giá trị lượng giác còn lại của góc $\alpha$.

Bài 4.(1,0 điểm)  Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60^0. Tàu thứ nhất chạy với vận tốc 40km/h, tàu thứ hai chạy với vận tốc 50km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

Bài 5.(1,0 điểm) Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (1 sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10người và 1,5 tấn hàng. Một chiếc xe loại A cho thuê với giá 5 triệu đồng, một chiếc xe loại B cho thuê với giá 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất.

Đáp án Đề thi Giữa kì 1 trường THPT Quế Sơn (Quảng Nam)

Xem thử Đề GK1 Toán 10 KNTT Xem thử Đề GK1 Toán 10 CTST Xem thử Đề GK1 Toán 10 CD

Xem thêm đề thi Giữa kì 1 Toán 10 năm 2023-2024 Quảng Nam hay khác:

• Đề thi Giữa kì 1 Toán 10 năm 2023-2024 trường THPT Võ Nguyên Giáp (Quảng Nam)

• Đề thi Giữa kì 1 Toán 10 năm 2023-2024 trường THPT Lê Hồng Phong (Quảng Nam)

Để học tốt lớp 10 các môn học sách mới:

• Giải bài tập Lớp 10 Kết nối tri thức
• Giải bài tập Lớp 10 Chân trời sáng tạo
• Giải bài tập Lớp 10 Cánh diều

---