40+ Đề thi Giữa kì 1 Toán 10 Cánh diều (có đáp án)
Với bộ 40+ Đề thi Giữa kì 1 Toán 10 Cánh diều năm 2026 có đáp án theo cấu trúc mới được biên soạn và chọn lọc từ đề thi Toán 10 của các trường THPT trên cả nước. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi Giữa học kì 1 Toán 10.
40+ Đề thi Giữa kì 1 Toán 10 Cánh diều (có đáp án)
Chỉ từ 150k mua trọn bộ Đề thi Toán 10 Giữa kì 1 Cánh diều theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Đề thi Giữa kì 1 Toán 10 Cánh diều (Giáo viên VietJack)
Đề thi Giữa kì 1 Toán 10 năm 2025-2026 (trên cả nước)
Đề thi Giữa kì 1 Toán 10 TH-THCS-THPT Lê Thánh Tông năm 2025-2026
Đề thi Giữa kì 1 Toán 10 THPT Trần Phú - Hoàn Kiếm năm 2025-2026
Đề thi Giữa kì 1 Toán 10 THPT Chuyên Lương Văn Tụy năm 2025-2026
Đề thi Giữa kì 1 Toán 10 THPT Ninh Bình – Bạc Liêu năm 2025-2026
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Câu nào là một mệnh đề?
A. 13 là số nguyên tố.
B. Bây giờ là mấy giờ?
C. Cảnh báo đường trơn, lái xe cẩn thận!
D. Các em phải học hành chăm chỉ nhé!
Câu 2. Khẳng định nào sau đây là đúng?
A. .
B. .
C. .
D. .
Câu 3.Cho hai tập hợp x = {2; 4; 8; 10; 12} và Y = {3; 4; 5; 6; 7; 8; 9}. Khi đó tập X \ Y hợp có bao nhiêu phần tử?
A. 3.
B. 4.
C. 5.
D. 6.
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. 3x 2y ≥ 0.
B. x2 + y2 < 2.
C. 2x2 + 3y > 0.
D. x + y2 ≥ 0.
Câu 5. Điểm O(0; 0) không thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A. .
B. .
C. .
D. .
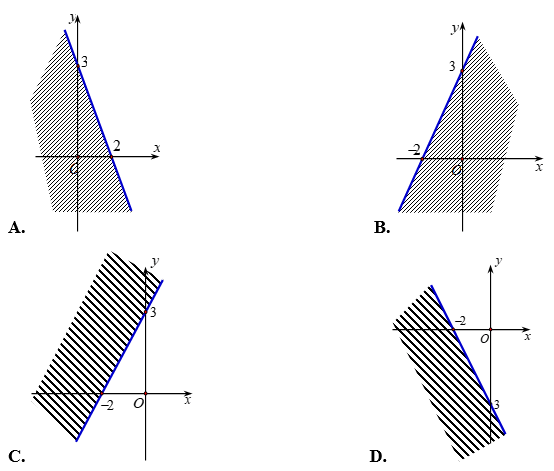
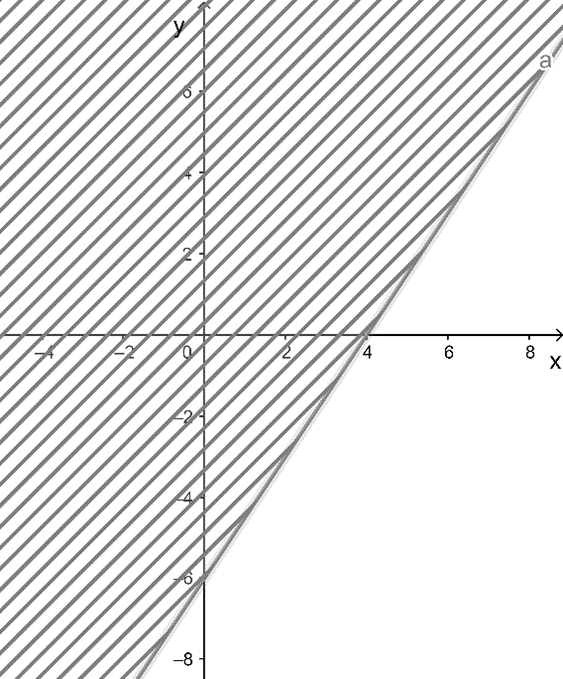
Câu 6. Miền nghiệm của bất phương trình 3x 2y ≥ 6 là
Câu 7.Tìm tập xác định của hàm số
A. .
B. .
C. .
D. .
Câu 8.Trong các hàm số sau hàm số nào là hàm số bậc hai?
A.
B.
C.
D. y = 3x + 2.
Câu 9. Cho hàm số bậc hai y = f(x) có đồ thị như hình vẽ. Tập nghiệm của bất phương trình f(x) > 0 là
A. (0; 3).
B. [-1; 3].
C. .
D. (-1; 3).
Câu 10. Cho góc α tù. Khẳng định nào sau đây là đúng?
A. cos α < 0.
B. cot α > 0.
C. sin α < 0.
D. tan α > 0.
Câu 11.Cho có . Tính diện tích tam giác ABC
A. S = 10.
B. .
C. S = 5.
D. .
Câu 12. Cho có . Độ dài cạnh BC là
A. .
B. .
C. .
D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Các câu sau là đúng hay sai?
a) Cho hai mệnh đề P: “Tứ giác ABCD là hình vuông” và mệnh đề Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”. Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề: “Nếu ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình vuông”.
b) { và }.
c) Mệnh đề phủ định của mệnh đề là .
d) Lớp 10A có tất cả 40 học sinh trong đó có 13 học sinh chỉ thích đá bóng, 18 học sinh chỉ thích chơi cầu lông và số học sinh còn lại thích chơi cả hai môn thể thao nói trên. Vậy, có 27 học sinh thích chơi cả hai môn cầu lông và đá bóng.
Câu 2. Cho hệ bất phương trình (I). Khi đó:
a) Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) (3; 2) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình là miền tam giác.
d) x= 1; y = 3 là nghiệm của hệ bất phương trình (I) sao cho F = 3x - y đạt giá trị lớn nhất.
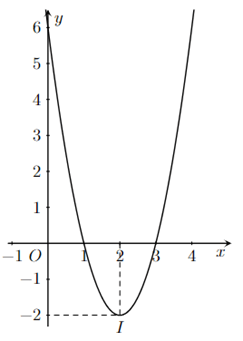
Câu 3. Cho đồ thị hàm số bậc hai y = f(x) có dạng như hình bên:
Các câu sau đúng hay sai?
a) Trục đối xứng của đồ thị là đường thẳng x = -2..
b) Đỉnh I của đồ thị hàm số có tọa độ là (2; -2).
c) Đường thẳng y = m + 2 cắt đồ thị hàm số tại hai điểm phân biệt khi và chỉ khi m > -1.
d) Hàm số đã cho là y = 2x2 - 2x + 6.
Câu 4. Cho có . Các mệnh đề sau đúng hay sai?
a) .
b) .
c) .
d) .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Câu 1. Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10A đưa ra ba nhóm ngành cho học sinh lựa chọn đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có 6 học sinh chọn nhóm ngành Giáo dục, 9 học sinh chọn nhóm ngành Y tế, 10 học sinh chọn nhóm ngành Công nghệ thông tin, 22 học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có 3 học sinh chọn hai nhóm ngành Giáo dục và Y tế, 2 học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, 3 học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Hỏi có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10A có 40 học sinh.
Câu 2. Bạn Nam tiết kiệm được 450 nghìn đồng. Trong đợt ủng hộ các bạn học sinh đồng bào miền Trung bị lũ lụt vừa qua, bạn Nam đã ủng hộ x tờ tiền loại 20 nghìn đồng, y tờ tiền loại 10 nghìn đồng. Khi đó bất phương trình biểu diễn tổng số tiền mà bạn Nam đã ủng hộ có dạng ax + by ≤ c. Tính giá trị của biểu thức P = c - 2a - b.
Câu 3. Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi thu được khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900. Gọi lần lượt là số radio kiểu một và radio kiểu hai sản xuất được trong một ngày để tiền lãi thu được là nhiều nhất. Tính tổng .
Câu 4. Một cửa hàng kinh doanh giày và giá để nhập một đôi giày là 40 đô la. Theo nghiên cứu của bộ phận kinh doanh thì nếu cửa hàng bán mỗi đôi giày với giá x đô la thì mỗi tháng sẽ bán được 120 - x đôi giày. Hỏi cửa hàng bán giá bao nhiêu cho một đôi giày để có thể thu lãi cao nhất trong tháng?.
Câu 5. Cho . Tính giá trị của biểu thức
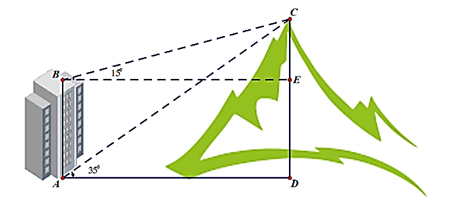
Câu 6. Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang 15° (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 60 (m) (làm tròn đến hàng phần trăm).
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
I. PHẦN TRẮC NGHIỆM
Câu 1: Trong các câu dưới đây, câu nào là mệnh đề ?
A. Hà Nội là thủ đô của Việt Nam.
B. Hôm nay là thứ mấy ?
C. Mệt quá !
D. Mấy giờ rồi ?
Câu 2: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A. 5 là số tự nhiên chẵn;
B. 5 là số nguyên tố;
C. 5 là số nguyên âm;
D. 5 là số chia hết cho 3.
Câu 3: Cho tập hợp A = {1; 3; 5; 7; 9}. Số phần tử của tập hợp A là
A. 6;
B. 4;
C. 5;
D. 3.
Câu 4: Cho tập hợp B = . Mệnh đề nào dưới đây đúng ?
A. B = [a; b];
B. B = (a; b];
C. B = [a; b) ;
D. B = (a; b).
Câu 5: Tập xác định của hàm số f(x)= là
A. D = [2; +∞);
B. D = (2; +∞);
C. D = (– ∞; 2);
D. D = (– ∞; 2].
Câu 6: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đồ thị của hàm số y= ?
A. P(4; 2);
B. M(1; – 1);
C. N(2; 4);
D. Q(2; – 4).
Câu 7: Cho hàm số f(x) = x3 – 2. Giá trị f(1) bằng bao nhiêu?
A. 3;
B. – 1;
C. 2;
D. 1
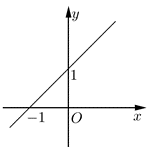
Câu 8: Hàm số nào dưới đây có đồ thị là đường thẳng như trong hình bên ?
A. y = x + 1;
B. y = x – 1;
C. y = – x + 1;
D. y = – x – 1.
Câu 9: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A. Đồ thị hàm số chẵn nhận đường thẳng y = x làm trục đối xứng.
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.
C. Đồ thị hàm số chẵn nhận nhận đường thẳng y = – x làm trục đối xứng.
D. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
Câu 10: Trong mặt phẳng Oxy, biết điểm M(2; y0) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y0 bằng:
A. 2;
B. 0;
C. – 1;
D. 1.
Câu 11: Trong mặt phẳng Oxy đồ thị của hàm số y = x2 – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?
A. x = 1;
B. x = – 1;
C. x = 2;
D. x = – 2.
Câu 12: Cho các vectơ như trong hình:
Mệnh đề nào dưới đây là đúng?
A. Hai vectơ và cùng hướng;
B. Hai vectơ và cùng hướng;
C. Hai vectơ và ngược hướng;
D. Hai vectơ và ngược hướng.
Câu 13: Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là:
A. AB;
B. BA;
C.
D.
Câu 14: Cho I là trung điểm của đoạn thẳng AB và M là một điểm tùy ý. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Câu 15: Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là
A. 2;
B. 3;
C. 1;
D. 6.
Câu 16: Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó A B là tập hợp nào dưới đây ?
A. [– 2; 3);
B. [1; 3);
C. [1; 3];
D. (– 2; 5).
Câu 17: Hàm số f(x) = x2 đồng biến trên khoảng nào dưới đây ?
A. (0; +∞);
B. (– 4; +∞);
C. (– ∞; 0);
D. (– ∞; – 1).
Câu 18: Cho hình chữ nhật ABCD có AB = 3a, BC = 4a. Độ dài của vectơ bằng
A. 25a;
B. 7a;
C. 5a;
D. a.
Câu 19: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.
A. (2; 8);
B. (– 10; – 3);
C. (3; 3);
D. (0; 2).
Câu 20: Cặp số nào sau đây không là nghiệm của hệ bất phương trình -3x+5y6
A. (0; 0);
B. (1; 1);
C. (– 1; 1);
D. (– 1; – 1).
Câu 21: Cho 0° < α < 180°. Chọn câu trả lời đúng.
A. cosα < 0.
B. sinα > 0.
C. tanα < 0.
D. cotα > 0.
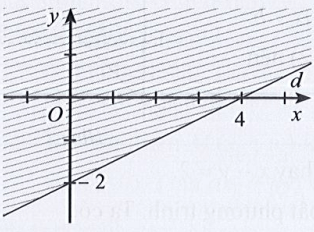
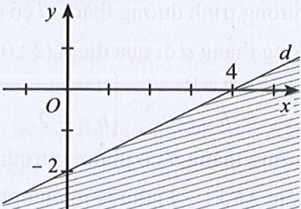
Câu 22: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?
A.
B.
C.
D.
Câu 23: Giá trị biểu thức T = sin225° + sin275° + sin2115° + sin2165° là:
A. T = sin 25°;
B. T = sin 75°;
C. T = 1;
D. T = 2.
Câu 24: Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, =125° . Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
A. BC ≈ 177,9;
B. BC ≈ 13,3;
C. BC ≈ 51,1;
D. BC ≈ 7,1.
Câu 25: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?
A. (0; 0);
B. (3; 0);
C. (1; – 2);
D. (– 3; – 4).
II. PHẦN TỰ LUẬN
Câu 1: Giải tam giác ABC biết ABC có b = 14, c = 25 và = 120°.
Câu 2: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 20 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 12km. Góc tạo bởi dây AC và CB là 75°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
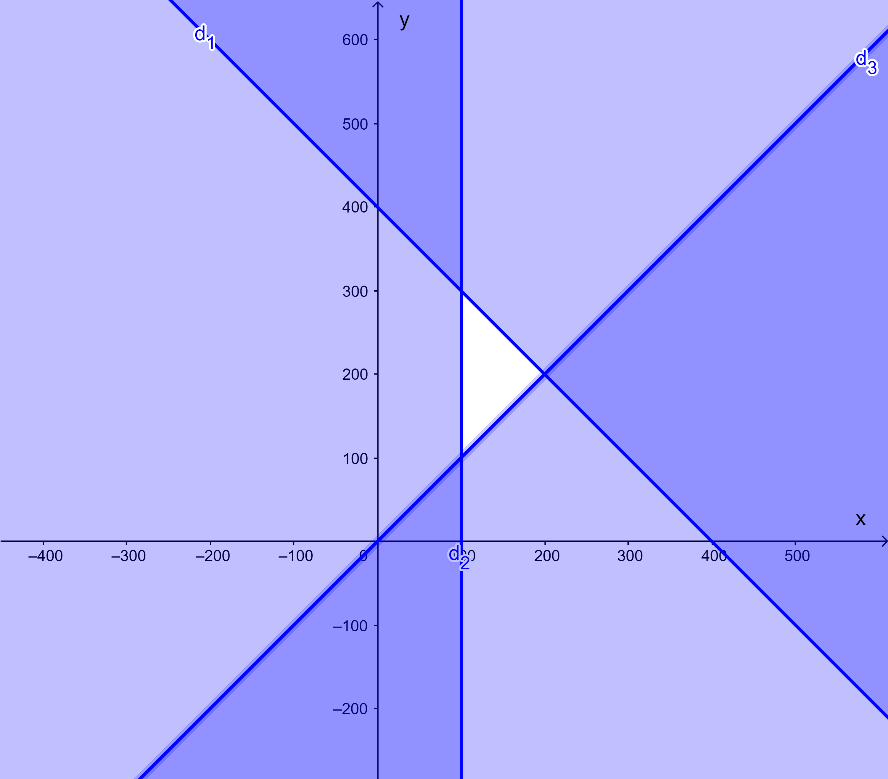
Câu 3: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.
Lời giải
Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).
Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.
Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.
Từ đó ta có hệ bất phương trình sau: .
Ta vẽ bốn đường thẳng:
d1: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);
d2: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);
d3: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).
Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với như hình vẽ sau:
Câu 4: Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?
-------------HẾT ----------
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?
A. {a} ⊂ A;
B. {a} ∈ A;
C. a ∈ A;
D. .
Câu 2. Cho mệnh đề chứa biến P(n): “n2 chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:
A. P(5);
B. P(2);
C. P(4);
D. P(6).
Câu 3. Mệnh đề phủ định của mệnh đề “Phương trình ax2 + bx + c = 0 (a ≠ 0) vô nghiệm” là:
A. Phương trình ax2 + bx + c = 0 (a ≠ 0) không có nghiệm;
B. Phương trình ax2 + bx + c = 0 (a ≠ 0) có nghiệm;
C. Phương trình ax2 + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt;
D. Phương trình ax2 + bx + c = 0 (a ≠ 0) có nghiệm kép.
Câu 4. Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm AB
A. A B = (1;2);
B. A B = [1;2);
C. A B = [1;2];
D. A B = (-2;1).
Câu 5. Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?
A. {5; 6};
B. {2; 3; 4};
C. {1; 2};
D. {0; 1; 5; 6}.
Câu 6: Số phần tử của tập hợp A = {k2 + 1| k ∈ ℤ, |k| ≤ 2} bằng
A. 1;
B. 5;
C. 3;
D. 2.
Câu 7: Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là
A. (2; 3];
B. (2; 3);
C. [2; 3);
D. [2; 3].
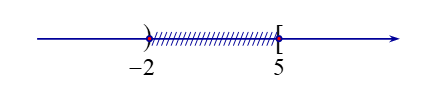
Câu 8: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. (– ∞; – 2) ∪ [5; +∞);
B. (– ∞; – 2) ∪ (5; +∞);
C. (– ∞; – 2] ∪ (5; +∞);
D. (– ∞; – 2] ∪ [5; +∞).
Câu 9. Lớp 10A1 có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A1 là:
A. 15;
B. 23;
C. 7;
D. 9.
Câu 10. Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?
A. (0; – 2);
B. (3; 0);
C. (2; 1);
D. (– 1; – 1).
Câu 11. Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?
A. 8 – x ≤ 0;
B. 4x – 3 > 0;
C. x – 3 < 0;
D. (x + 1)2 ≥ 1.
Câu 12. Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?
A. ;
B. ;
C. ;
D. .
Câu 13. Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:
A. 0,57;
B. 1;
C. ;
D. 0,15.
Câu 14. Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°
A. ;
B. – 0,5;
C. 1;
D. 0.
Câu 15. Cho tam giác ABC, ta có các đẳng thức:
(I) sin = sin;
(II) tan = cot;
(III) sinA = sin(B + C).
Có bao nhiêu đẳng thức đúng?
A. ;
B. – 0,5;
C. 1;
D. 0.
Câu 16. Cho điểm M(x0; y0) nằm trên đường tròn đơn vị thỏa mãn . Khi đó phát biểu nào dưới đây là sai?
A. sinα = x0;
B. cosα = x0;
C. tanα = ;
D. cotα = .
Câu 17. Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, ha, hb, hc lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.
A. SABC = pr;
B. SABC = c.a.sinA;
C. SABC = ;
D. SABC = .
Câu 18. Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:
A. ;
B. ;
C. a.cosA = b.cosB = c.cosC;
D. a.sinA = b.sinB = c.sinC.
Câu 19. Cho tam giác ABC có BC = 50 cm, . Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét). Chu vi của tam giác ABC là:
A. 135,84;
B. 67,92;
C. 131,91;
D. 65,96.
Câu 20. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được . Chiều cao của cây gần với kết quả nào nhất sau đây?
A. 38m;
B. 39m;
C. 19m;
D. 20m.
Câu 21. Đẳng thức nào sau đây, mô tả đúng hình vẽ bên?
A. .
B. .
C. .
D. .
Câu 22: Cho hình chữ nhật ABCD. Hãy chọn khẳng định đúng.
A. .
B. .
C. .
D. .
Câu 23. Cho hình bình hành ABCDvới điểm Kthỏa mãn thì
A. K là trung điểm của AC.
B. K là trung điểm của AD.
C. K là trung điểm của AB.
D. K là trung điểm của BD.
Câu 24. Cho tam giác đều ABCcó AB=a, M là trung điểm của BC. Khi đó bằng
A. .
B. 2a.
C. .
D. a.
Câu 25. Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?
A. .
B. .
C. .
D. .
Câu 26. Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:
A. ;
B. ;
C. ;
D. .
Câu 27. Phát biểu nào sau đây là sai?
A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
B. Vectơ là đoạn thẳng có hướng.
C. Hai vectơ cùng hướng thì cùng phương.
D. Hai vectơ cùng phương thì cùng hướng.
Câu 28. Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 29. Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ bằng
A. 1;
B. 6;
C. ;
D. 3.
Câu 30. Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ bằng
A. a;
B. 2a;
C. ;
D. .
...............................
...............................
...............................
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
PHẦN I: TRẮC NGHIỆM (5 điểm)
Câu 1. Cho hình vuông ABCD có cạnh là 2a, O là giao điểm của hai đường chéo. Tính .
A. ;
B. ;
C. ;
D. .
Câu 2. Cho tập hợp A = {a; b; c; d; e; f}. Có bao nhiêu tập con của tập A có 2 phần tử.
A. 64;
B. 6;
C. 15;
D. 20.
Câu 3. Hệ bất phương trình nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
A. ;
B. ;
C. ;
D. 5x + 9y < – 10.
Câu 4. Cho hình bình hành ABCD, khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 5. Câu nào sau đây không là mệnh đề?
A. 4 là số nguyên tố;
B. Ngày mùng 2 tháng 9 hàng năm là ngày quốc khánh nước Việt Nam;
C. Một tuần có bảy ngày;
D. Mấy giờ rồi?
Câu 6. Cho tập hợp M = [– 3; 7] ∩ (2; 5) và N = (– ∞; 2] \ [1; 3). Phát biểu nào dưới đây là đúng?
A. M ⊂ N;
B. N ⊂ M;
C. M = N;
D. Cả A, B, C đều sai.
Câu 7. Cho hai tập hợp P = [– 4; 5) và Q = (– 3; +∞). Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 8. Cho tam giác ABC, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 9. Cho ∆ABC có trọng tâm G. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 10. Mệnh đề phủ định của mệnh đề P: “∃x ∈ ℝ, x2 + 1 ≤ 0” và xét tính đúng sai của mệnh đề đó?
A. : “∃x ∈ ℝ, x2 + 1 < 0” và là mệnh đề sai.
B. : “∃x ∈ ℝ, x2 + 1 ≥ 0” và là mệnh đề đúng.
C. : “∀x ∈ ℝ, x2 + 1 > 0” và là mệnh đề đúng.
D. : “∀x ∈ ℝ, x2 + 1 < 0” và là mệnh đề sai.
Câu 11. Cho I là trung điểm đoạn thẳng AB. Khẳng định nào sau đây đúng?A. .
B. .
C. .
D. .
Câu 12. Hãy liệt kê các phần tử của tập A = {x ∈ ℤ|2x2 – 5x + 2 = 0}.
A. A = { – 2};
B. ;
C. A = {2};
D. .
Câu 13. Cho tam giác ABC. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 14. Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. 12 là số nguyên tố;
B. 9 là số nguyên tố;
C. 4 là số nguyên tố;
D. 5 là số nguyên tố.
Câu 15. Tìm giá trị lớn nhất của hàm số F(x; y) = 2x + 3y với cặp (x; y) thuộc miền nghiệm của hệ bất phương trình .
A. 0;
B. 4;
C. – 12;
D. 12.
Câu 16. Cho tập hợp . Khẳng định nào sau đây đúng ?
A. ;
B. ;
C. ;
D. .
Câu 17. Cho hai vectơ tùy ý , và hai số thực h, k bất kì. Khẳng định nào sau đây sai?
A. .
B. .
C. .
D. .
Câu 18. Hai vectơ bằng nhau khi chúng thỏa mãn điều kiện:
A. Cùng phương và cùng độ dài.
B. Ngược hướng và cùng độ dài.
C. Cùng độ dài.
D. Cùng hướng và cùng độ dài.
Câu 19. Cho các cặp số: (0; 1), (– 3; 2), (7; 2), ( – 8; – 1). Có bao nhiêu cặp số thỏa mãn là nghiệm của bất phương trình y ≥ 2x – 5?
A. 0;
B. 1;
C. 2;
D. 3.
Câu 20. Cho A = {x ∈ ℝ| – 1 < x < 4}, B = {x ∈ ℝ| |x| ≤ 3}. Khi đó A ∩ B là:
A. [– 1; 3];
B. (– 1; 3];
C. [– 3; 4];
D. [3; 4).
Câu 21. Cho hình chữ nhật ABCD Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Câu 22. Mệnh đề phủ định của mệnh đề ∀x ∈ ℝ, x2 + x + 2021 > 0 là:
A. ∀x ∈ ℝ, x2 + x + 2021 ≤ 0;
B. ∀x ∈ ℝ, x2 + x + 2021 < 0;
C. ∃x ∈ ℝ, x2 + x + 2021 ≤ 0;
D. x ∈ ℝ, x2 + x + 2021 > 0.
Câu 23. Cho tam giác đều ABC có cạnh bằng a. Tính .
A. a;
B. 2a;
C. ;
D. .
Câu 24. Cho tam giác ABC có AB = 6; AC = 7; BC = 8. Số đo của góc :
A. 75°31’;
B. 46°34’;
C. 57°55’;
D. 90°21’.
Câu 25. Cho tam giác ABC có AB = 3,6; AC = 4,5; . Bán kính đường tròn ngoại tiếp tam giác ABC gần nhất với giá trị nào sau đây:
A. 7,0;
B. 7,2;
C. 4,0;
D. 4,4.
PHẦN II: TỰ LUẬN (5 điểm)
Bài 1. (2 điểm)
a) Biểu diễn miền nghiệm của bất phương trình: 3x – 2y > 0.
b) Một phân xưởng may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may áo vest hết 2m vải và cần 20 giờ; 1 quần âu hết 1,5m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 900m vải và số giờ công không vượt quá 6 000 giờ. Theo khảo sát thị trường, số lượng quần bán ra không nhỏ hơn số lượng áo và không vượt quá 2 lần số lượng áo. Khi xuất ra thị trường, một chiếc áo lãi 350 nghìn đồng, 1 chiếc quần lãi 100 nghìn đồng. Phân xưởng cần may bao nhiêu áo vest và quần âu để thu được tiền lãi cao nhất (biết thị trường tiêu thụ luôn đón nhận sản phẩm của xí nghiệp).
Bài 2. (2 điểm)
a) Cho ∆ABC có trọng tâm G. Gọi P, Q là các điểm thỏa mãn , . Chứng minh rằng ba điểm P, Q, G thẳng hàng.
b) Cho ∆ABC có và BC = 8. Tính diện tích tam giác ABC.
Bài 3. (1 điểm) Cho , với m là tham số. Tìm m để là một nửa khoảng.
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
I. PHẦN TRẮC NGHIỆM (5,0 điểm)
Câu 1: Cho M là trung điểm đoạn thẳng AB và điểm O tùy ý. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 2: Phát biểu nào sau đây là một mệnh đề?
A. Thời tiết hôm nay lạnh quá!;
B. x + 3 = 2;
C. Số -3có phải là số tự nhiên không?;
D. Gia Lai là một tỉnh của Việt Nam.
Câu 3: Tập hợp A = {x ∈ ℤ | – 4 < x < 5} và B = {x ∈ ℕ |x2 – 9 = 0}. Số tập con của tập hợp A\B là:
A. 256;
B. 128;
C. 64;
D. 32.
Câu 4: Lập mệnh đề phủ định của mệnh đề ”∀x ∈ ℝ, x2 > 0”.
A. ∃x ∈ ℝ, x2 ≤ 0;
B. ∃x ∈ ℝ, x2 ≥ 0;
C. ∀x ∈ ℝ, x2 ≥ 0;
D. ∃x ∈ ℝ, x2 < 0.
Câu 5: Cho vectơ có độ dài bằng 2. Khi đó vectơ :
A. có độ dài bằng -6và cùng hướng với vectơ .
B. có độ dài bằng -6và ngược hướng với vectơ .
C. có độ dài bằng 6 và cùng hướng với vectơ .
D. có độ dài bằng 6 và ngược hướng với vectơ .
Câu 6: Cho bất phương trình bậc nhất hai ẩn 5x – 3y < 2. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình đã cho?
A. M(2; 1);
B. N(1; 2);
C. P(1; 0);
D. Q(0; – 1).
Câu 7: Cho 3 điểm M,N,Ptùy ý. Khi đó bằng vectơ nào sau đây?
A. .
B. .
C. .
D. .
Câu 8: Liệt kê các phần tử của tập hợp A = {x ∈ ℤ | |x – 2| < 3}.
A. A = { – 1; 0; 1; 2; 3; 4; 5};
B. A = { 0; 1; 2; 3; 4; 5};
C. A = { – 1; 0; 1; 2; 3; 4};
D. A = { 0; 1; 2; 3; 4}.
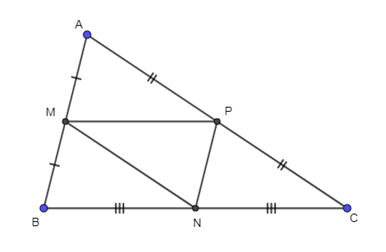
Câu 9: Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của BC, P là trung điểm của AC. Nhận xét nào dưới đây là sai?
A. ;
B. ;
C. ;
D. .
Câu 10: Mệnh đề phủ định của mệnh đề “∀x ∈ ℝ: x2 > x + 3” là
A. “∃x ∈ ℝ: x2 > x + 3”;
B. “∀x ∈ ℝ: x2 ≤ x + 3”
C. “∃x ∈ ℝ: x2 ≤ x + 3”;
D. “∃x ∈ ℝ: x2 < x + 3”.
Câu 11: Điều kiện cần và đủ để hai vectơ bằng nhau là:
A. Hai vectơ cùng độ dài.
B. Hai vectơ cùng chiều và cùng độ dài.
C. Hai vectơ cùng hướng và cùng độ dài.
D. Hai vectơ cùng phương và cùng độ dài.
Câu 12:Cho hai tập hợp A = {– 3; 0; 4; 7}, B = {– 3; 4; 7; 17}. Khi đó tập A ∩ B là tập nào sau đây?
A.{4; 7};
B. {– 3; 0; 4; 7; 17};
C. {– 3; 4; 7};
D.{– 3; 7}.
Câu 13: Mệnh đề nào dưới đây là mệnh đề chứa biến?
A. |x| ≥ 0 với mọi x ∈ ℝ;
B. – x2 – 1 < 0 với mọi x ∈ ℝ;
C. x + 2y = 0.
D. luôn xác định với mọi giá trị thực của x.
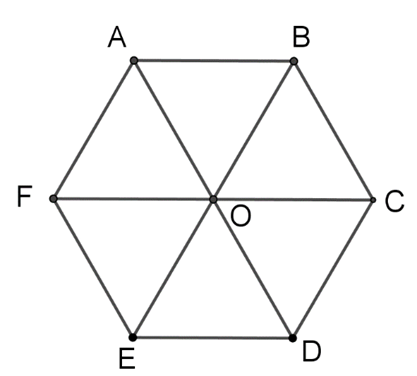
Câu 14: Cho lục giác đều ABCDEF có tâm O. Nhóm vectơ nào sau đây bằng vectơ ?
A. ;
B. ;
C. ;
D. .
Câu 15: Cho tam giác ABC có trọng tâm G. Gọi D là trung điểm của BC. Đẳng thức nào sau đây đúng?
A. .
B. .
C. .
D. .
Câu 16: Cho hình vuông ABCD có tâm O, độ dài cạnh bằng 4a. Tính độ dài vectơ .
A. .
B. .
C. .
D. .
Câu 17: Cho hai tập hợp A=[m-2;m+3), B=(-4;7]. Có bao nhiêu số nguyên m để .
A. 7.
B. 8.
C. 5.
D. 6.
Câu 18: Cho hình bình hành ABCD tâm O. Gọi M là điểm trên cạnh BC sao cho 4MB=3MC. Biểu diễn vectơ theo hai vectơ và .
A. ;
B. ;
C. ;
D. .
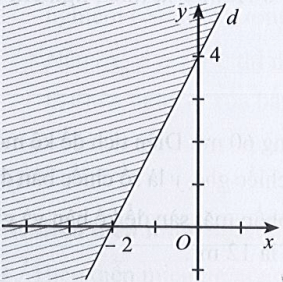
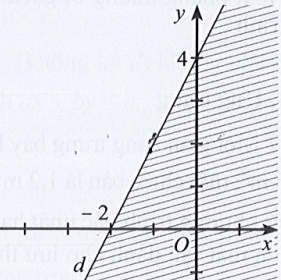
Câu 19: Phần không bị gạch (Hình vẽ bên) là miền nghiệm của bất phương trình nào dưới đây?
A. 2x – 3y ≤ – 12;
B. 2x – 3y ≥ – 12;
C. 3x – 2y ≤ 12;
D. 3x – 2y ≥ – 12.
Câu 20: Trong các cặp số sau: (7; 1), (2; – 1), (5; – 1), (6; – 2). Có bao nhiêu cặp số là nghiệm của hệ bất phương trình .
A. 0;
B. 1;
C. 2;
D. 3.
Câu 21: Cho tam giác ABC. Gọi M là điểm trên cạnh AB sao cho MA = 3MB và G là trọng tâm tam giác ABC. Hãy phân tích vectơ theo hai vectơ và .
A. ;
B. ;
C. ;
D.
Câu 22: Miền nghiệm của bất phương trình 3x ≥ 2 được biểu diễn bởi phần tô màu trong hình vẽ nào dưới đây?
A.
B.
C.
D.
Câu 23: Cặp số (0; – 19) là nghiệm của hệ bất phương trình nào dưới dây?
A. ;
B. ;
C. ;
D. .
Câu 24: Phát biểu nào dưới đây là sai?
A. Vectơ – không là vectơ cùng phương với mọi vectơ;
B. Có vô số vectơ cùng hướng với vectơ ;
C. Ba điểm A, B, C thẳng hàng khi và chỉ khi tồn tại k > 0 để ;
D. Nếu tồn tại k > 0 thỏa mãn thì hai vec tơ và cùng hướng.
Câu 25: Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu nói được một hoặc hai hoặc ba thứ tiếng: Nga, Anh hoặc Pháp. Biết rằng có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?
A. 18;
B. 22;
C. 20;
D. 28.
B – PHẦN TỰ LUẬN: (5,0 ĐIỂM)
Bài 1: (1,5 điểm)
a) Cho hai tập hợp A=, B=(-3;5]. Tìm
b) Tìm tập xác định D của hàm số . Tìm tập hợp .
Bài 2: (2,5 điểm):
a) Cho tam giác ABC có AB = 15, AC = 12 và . Tính diện tích tam giác ABC và bán kính đường tròn nội tiếp tam giác.
b) Hai tàu cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau theo hai hướng tạo với nhau một góc 80°. Tàu thứ nhất đi với tốc độ 12 hải lí một giờ, tàu thứ hai đi với tốc độ 9 hải lí một giờ. Sau 3 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí? (làm tròn kết quả đến hàng phần mười).
Bài 3: (1,0 điểm)
Cho tam giác ABC có trọng tâm G. Gọi M là điểm thỏa . Gọi N là điểm trên đường thẳng AB sao cho ba điểm M, G, N thẳng hàng. Tính tỉ số .
Xem thêm bộ đề thi Toán 10 Cánh diều năm 2025 hay khác:
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 10 (các môn học)
- Giáo án điện tử lớp 10 (các môn học)
- Giáo án Ngữ văn 10
- Giáo án Toán 10
- Giáo án Tiếng Anh 10
- Giáo án Vật Lí 10
- Giáo án Hóa học 10
- Giáo án Sinh học 10
- Giáo án Lịch Sử 10
- Giáo án Địa Lí 10
- Giáo án Kinh tế Pháp luật 10
- Giáo án Tin học 10
- Giáo án Công nghệ 10
- Giáo án Giáo dục quốc phòng 10
- Giáo án Hoạt động trải nghiệm 10
- Đề thi lớp 10 (các môn học)
- Đề thi Ngữ Văn 10 (có đáp án)
- Chuyên đề Tiếng Việt lớp 10
- Đề cương ôn tập Văn 10
- Đề thi Toán 10 (có đáp án)
- Đề thi cương ôn tập Toán 10
- Đề thi Toán 10 cấu trúc mới (có đáp án)
- Đề thi Tiếng Anh 10 (có đáp án)
- Đề thi Vật Lí 10 (có đáp án)
- Đề thi Hóa học 10 (có đáp án)
- Đề thi Sinh học 10 (có đáp án)
- Đề thi Lịch Sử 10 (có đáp án)
- Đề thi Địa Lí 10 (có đáp án)
- Đề thi Kinh tế & Pháp luật 10 (có đáp án)
- Đề thi Tin học 10 (có đáp án)
- Đề thi Công nghệ 10 (có đáp án)
- Đề thi Giáo dục quốc phòng 10 (có đáp án)

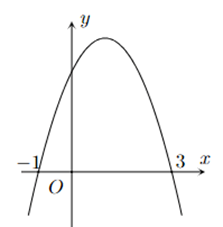










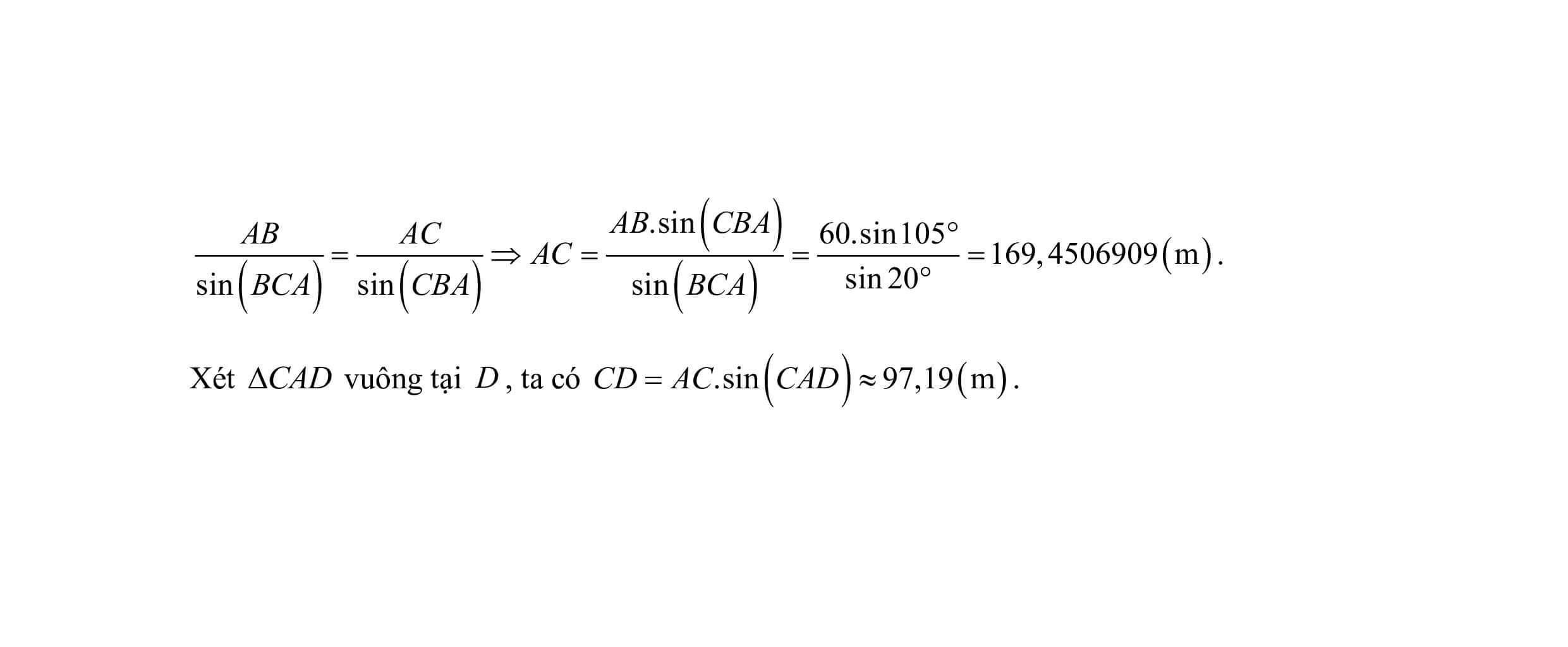




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

