(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Cấp số cộng. Cấp số nhân
Chuyên đề Cấp số cộng. Cấp số nhân trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Cấp số cộng. Cấp số nhân
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
(Ôn thi ĐGNL, ĐGTD) Cấp số cộng
I. LÝ THUYẾT CẦN NHỚ
1. Định nghĩa
Dãy số (un) là cấp số cộng nếu un = un-1 + d với n ≥ 2, d là số không đổi.
Số d được gọi là công sai của cấp số cộng, ta có d = un - un-1 với n ≥ 2.
Nếu d = 0 thì cấp số cộng là một dãy số không đổi.
2. Tính chất
Nếu (un) là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là .
Hệ quả: Ba số a, b, c (theo thứ tự đó) lập thành một cấp số cộng ⇔ a + c = 2b.
3. Số hạng tổng quát
Nếu một cấp số cộng có số hạng đầu u1 và công sai d thì số hạng tổng quát un của nó được xác định bởi công thức: un = u1 + (n-1)d.
4. Tổng n số hạng đầu của cấp số cộng
Giả sử (un) là một cấp số cộng có công sai d.
Gọi .
Ta có .
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Nhận dạng một dãy số là cấp số cộng
1.1. Phương pháp giải
Để chứng minh dãy số (un) là một cấp số cộng, ta xét d = un+1 - un
- Nếu d là hằng số thì (un) là một cấp số cộng với công sai d.
- Nếu d phụ thuộc vào n thì (un) không là cấp số cộng.
1.2. Ví dụ
Ví dụ 1. Dãy số nào dưới đây là cấp số cộng?
A. .
B. .
C. .
D. .
Hướng dẫn giải
Với dãy số , xét hiệu: un+1 - un = n + 1 + 2n+1 - n - 2 = 2n + 1, (n ∈ ℕ*) thay đổi theo n nên un = n + 2n, (n ∈ ℕ*) không là cấp số cộng. (A loại)
Với dãy số , xét hiệu: un+1 - un = 3(n + 1) + 1 - 3n - 1 = 3, (n ∈ ℕ*) là hằng số nên un = 3n + 1, (n ∈ ℕ*) là cấp số cộng. (B đúng)
Với dãy số , xét hiệu: un+1 - un = 3n+1 - 3n = 2.3n, (n ∈ ℕ*) thay đổi theo n nên un = 3n, (n ∈ ℕ*) không là cấp số cộng. (C loại)
Với dãy số , xét hiệu: = , (n ∈ ℕ*) thay đổi theo n nên không là cấp số cộng. (D loại)
Chọn B.
Ví dụ 2. Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A. un = 3n2 + 2017.
B. un = 3n + 2018.
C. un = 3n + 2017
D. un = (-3)n+1.
Hướng dẫn giải
Xét dãy số un = 3n + 2018, ta có un+1 - un = 3(n + 1) + 2018 - (3n + 2018) = 3 ⇔ un+1 = un + 3.
Vậy dãy số trên là cấp số cộng có công sa d = 3. Chọn B.
2. Dạng toán 2: Tìm số hạng đầu tiên, số hạng tổng quát, công sai và tính tổng n số hạng đầu tiên
2.1. Phương pháp giải
Cần lưu ý:
• Định nghĩa: (un) là cấp số cộng ⇔ (d: công sai).
• Số hạng tổng quát: un = u1 + (n - 1)d với n ≥ 2.
• Tính chất các số hạng: với k ≥ 2.
• Tổng n số hạng đầu tiên: Sn = u1 + u2 + ... + un = .
2.2. Ví dụ
Ví dụ 1. Tìm số hạng đầu tiên, công sai, số hạng thứ 50 và tổng của 20 số hạng đầu tiên của cấp số cộng (un) sau, biết rằng: .
Hướng dẫn giải
Áp dụng công thức un = u1 + (n - 1)d, ta có: .
Vậy số hạng đầu tiên u1 = 3, công sai d = 4.
Số hạng thứ 50: u50 = u1 + 49d = 3 + 49.4 = 199.
Tổng của 20 số hạng đầu tiên: = 10(2.3 + 49.4) = 2020.
Ví dụ 2. Cho cấp số cộng (un) biết un = 9 - 5n. Tìm S100.
Hướng dẫn giải
3. Dạng toán 3: Ứng dụng cấp số cộng vào chứng minh đẳng thức, giải phương trình
3.1. Phương pháp giải
Áp dụng tính chất: Ba số a, b, c (theo thứ tự đó) lập thành một cấp số cộng ⇔ a + c = 2b.
3.2. Ví dụ
Ví dụ 1. Cho a, b, c là ba số hạng liên tiếp của một cấp số cộng, chứng minh rằng:
a) a2 + 2bc = c2 + 2ab.
b) a2 + 8bc = (2b + c)2.
Hướng dẫn giải
a) Vì a, b, c là ba số hạng liên tiếp của một cấp số cộng: a + c ⇔ a = 2b - c.
Ta có a2 - 2ab = a2 - a(a + c) = -ac = -c(2b - c) = c2 - 2bc.
Vậy a2 - 2ab = c2 - 2bc ⇔ a2 + 2bc = c2 + 2ab.
b) Ta có a2 + 8bc = (2b + c)2 + 8bc = 4b2 - 4bc + c2 + 8bc = 4b2 + 4bc + c2 = (2b + c)2.
Ví dụ 2. Tìm giá trị m để phương trình (x2 + 2x - 3)(x - 2m) = 0 có 3 nghiệm phân biệt lập thành một cấp số cộng có công sai lớn hơn 2.
Hướng dẫn giải
Ta có: (x2 + 2x - 3)(x - 2m) = 0 ⇔ .
Ba nghiệm này lập thành một cấp số cộng có công sai lớn hơn 2 nên có 3 trường hợp:
TH1: Ba nghiệm thứ tự là -3;1;2m. Suy ra (thỏa mãn).
TH2: Ba nghiệm thứ tự -3;2m;1. Suy ra (loại).
TH3: Ba nghiệm thứ tự 2m;-3;1. Suy ra (thỏa mãn).
Ví dụ 3. Tìm m để phương trình x4 - 20x2 + (m - 1)2 = 0 có bốn nghiệm phân biệt lập thành cấp số cộng.
Hướng dẫn giải
Đặt . Phương trình trở thành: (1).
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Cho cấp số cộng (un) thỏa mãn . Tìm u1, d?
A. .
B. .
C. .
D. .
Câu 2. Một cấp số cộng có u3 = -15 và u14 = 18. Tổng của 50 số hạng đầu của cấp số cộng này là
A. 2 025.
B. 2 425.
C. 2 225.
D. 2 625.
Câu 3. Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng.
A. 8; 13; 18.
B. 6; 12; 18.
C. 7; 12; 17.
D. 6; 10; 14.
Câu 4. Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
A. .
B. .
C. .
D. .
Câu 5. Tìm m để 3 số: 4; 5m + 1; 32 - 7m theo thứ tự lập thành cấp số cộng.
A. m = 2.
B. m = 11.
C. m = 1.
D. m = -2.
Câu 6. Cho cấp số cộng (un) thỏa mãn . Tính .
A. .
B. 2021.
C. 1010.
D. 2020.
Câu 7. Cho cấp số cộng (un) thỏa mãn . Tính .
A. 2 043 230.
B. 2 043 905.
C. 2 042 220.
D. 2 043 231.
Câu 8. Cho ba số dương a, b, c lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. a2 - c2 = 2ab + 2bc - 2ac.
B. a2 + c2 = 2ab + 2bc + 2ac.
C. a2 + c2 = 2ab + 2bc - 2ac.
D. a2 - c2 = 2ab - 2bc + 2ac.
Câu 9. Cho cấp số cộng (un) với số hạng đầu là u1 = -2017 và công sai d = 3. Bắt đầu từ số hạng nào trở đi mà các số hạng của cấp số cộng đều nhận giá trị dương?
A. u675.
B. u673.
C. u674.
D. u672.
Câu 10. Người ta trồng 465 cây trong một khu vườn hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ ba có 3 câu, ... Số hàng cây trong khu vườn là
A. 30.
B. 31.
C. 29.
D. 28.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Sinh nhật bạn của An vào ngày 01 tháng năm. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo 100 đồng vào ngày 01 tháng 01 năm 2016, sau đó cứ liên tục ngày sau hơn ngày trước 100 đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền? (thời gian bỏ ống heo tính từ ngày 01 tháng 01 năm 2016 đến ngày 30 tháng 4 năm 2016).
|
Điền đáp án |
|
Câu 17. Có bao nhiêu giá trị thực của tham số A để phương trình có bốn nghiệm phân biệt lập thành cấp số cộng.
|
Điền đáp án |
|
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai.
Câu 19. Cho dãy số (un) có .
a) (un) không phải là một cấp số cộng.
b) (un) là cấp số cộng có .
c) Số hạng thứ n + 1 của dãy là: .
d) Hiệu .
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Cấp số nhân
I. LÝ THUYẾT CẦN NHỚ
1. Định nghĩa
Dãy số (un) là cấp số nhân nếu un = un-1.q với n ≥ 2, q là số không đổi.
Số q được gọi là công bội của cấp số nhân. Nếu un ≠ 0 với mọi n ∈ ℕ* thì với n ≥ 2.
Đặc biệt:
- Khi q = 0, cấp số nhân có dạng u1, 0, 0, ..., 0, ...
- Khi q = 1, cấp số nhân có dạng u1, u1, u1, ..., u1, ...
- Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, ..., 0, ...
2. Số hạng tổng quát
Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức un = u1.qn-1 với n ≥ 2.
3. Tính chất
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là với k ≥ 2.
Hệ quả: Ba số a, b, c theo thứ tự đó lập thành một cấp số nhân ⇔ ac = b2.
4. Tổng n số hạng đầu của cấp số nhân
Cho cấp số nhân (un) có số hạng đầu u1 và công bội q (q ≠ 1). Đặt , ta có:
.
Lưu ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1, ..., u1, ... khi đó Sn = nu1.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Nhận dạng một dãy số là cấp số nhân
1.1. Phương pháp giải
Để chứng minh một dãy số là cấp số nhân:
• Nếu thì ta lập tỉ số :
+) k là hằng số thì (un) là cấp số nhân có công bội q = k.
+) k phụ thuộc vào n thì (un) không là cấp số nhân.
• Để chứng minh dãy (un) không phải là cấp số nhân, ta chỉ cần chỉ ra ba số hạng liên tiếp không tạo thành cấp số nhân, chẳng hạn .
• Để chứng minh a, b, c theo thứ tự đó lập thành cấp số nhân, ta chứng minh: ac = b2 hoặc .
1.2. Ví dụ
Ví dụ 1. Trong các dãy số (un) sau, dãy nào là cấp số nhân?
A. .
B. .
C. .
D. .
Hướng dẫn giải
Xét từng đáp án:
Đáp án A: , không phải là hằng số. Vậy (un) không phải là cấp số nhân.
Đáp án B: = , không phải là hằng số. Vậy (un) không phải là cấp số nhân.
Đáp án C: Từ công thức truy hồi của dãy số, suy ra u1 = 2; u2 = 3; u3 = 2; u4 = 3;...
Vì nên (un) không phải là cấp số nhân.
Đáp án D: . Vậy (un) là một cấp số nhân.
Chọn D.
Ví dụ 2. Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào là một cấp số nhân?
A. un = 7 - 3n.
B. un = 7 - 3n.
C. un = .
D. un = 7.3n.
Hướng dẫn giải
Dãy un = 7.3n là cấp số nhân có . Chọn B.
2. Dạng toán 2: Tìm số hạng đầu tiên, số hạng tổng quát, công bội và tính tổng n số hạng đầu tiên
2.1. Phương pháp giải
Cần lưu ý:
• Định nghĩa: (un) là cấp số nhân ⇔ un+1 = un.q với n ∈ ℕ* (q: công bội).
• Số hạng tổng quát: un = u1.qn-1 với n ≥ 2.
• Tính chất các số hạng: với k ≥ 2.
• Tổng n số hạng đầu tiên: .
2.2. Ví dụ
Ví dụ 1. Cho cấp số nhân (un) có công bội nguyên và các số hạng thỏa mãn .
a) Tìm số hạng đầu và công bội của cấp số nhân.
b) Hỏi tổng bao nhiêu số hạng đầu tiên bằng 1365?
c) Số 4096 là số hạng thứ mấy?
Hướng dẫn giải
b) Ta có
Vậy tổng của 12 số hạng đầu tiên bằng 1365.
Vậy số 4096 là số hạng thứ 13.
Ví dụ 2. Tính các tổng sau:
a) .
b) .
Hướng dẫn giải
a) Ta có dãy số là một cấp số nhân với n số hạng, có số hạng đầu và công bội . Do đó
Dãy số là cấp số nhân với n số hạng, có số hạng đầu u1 = 32 và công bội .
Ví dụ 3. Tính tồng sau: .
Hướng dẫn giải
Ví dụ 4. Tìm m để phương trình x3 - (2m + 1)x2 + 14x - 8 = 0 có ba nghiệm lập thành cấp số nhân.
Hướng dẫn giải
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số nhân, khi đó:
=> (x2)3 = 8 => x2 = 2.
Thay vào phương trình ta có: m = 3.
Thay m = 3 vào phương trình ta thấy phương trình có 3 nghiệm: x1 = 1, x2 = 2, x3 = 4.
Vậy m = 3 là giá trị cần tìm.
3. Dạng toán 3: Ứng dụng cấp số nhân vào chứng minh đẳng thức, giải phương trình
3.1. Phương pháp giải
• Ba số a, b, c theo thứ tự đó lập thành một cấp số cộng ⇔ ac = b2.
• Tổng của n số hạng đầu tiên: khi q ≠ 1.
• Nếu là tổng của một cấp số nhân lùi thì ta có: .
3.2. Ví dụ
Ví dụ 1. Số đo bốn góc của một tứ giác lập thành cấp số nhân và góc cuối gấp 9 lần góc thứ hai. Tìm số đo của góc thứ nhất.
Hướng dẫn giải
Gọi A, B, C, D theo thứ tự đó là số đo các góc của tứ giác lập thành cấp số nhân với công bội q.
=> B = Aq; C = Aq2; D = Aq3.
Theo đề bài ta có: D = 9B ⇔ Aq3 = 9Aq ⇔ q2 = 9 ⇔ q = ±3.
Với q = -1 => B = -3A < 0 nên loại.
Với q = 3 ta có A + B + C + D = 360° ⇔ A = 3A + 9A + 27A = 360° ⇔ A = ⇔ 9°.
Ví dụ 2. Từ độ cao 55,8m của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng độ cao mà quả bóng đạt trước đó. Tính tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất.
Hướng dẫn giải
Gọi hn là độ dài đường đi của quả bóng ở lần rơi xuống thứ n(n ∈ ℕ*).
Gọi ln là độ dài đường đi của quả bóng ở lần nảy lên thứ n(n ∈ ℕ*).
Theo bài ra ta có và các dãy số (hn),(ln) là các cấp số nhân lùi vô hạn với công bội .
Suy ra tổng độ dài đường đi của quả bóng là: S = = 68,2 (m).
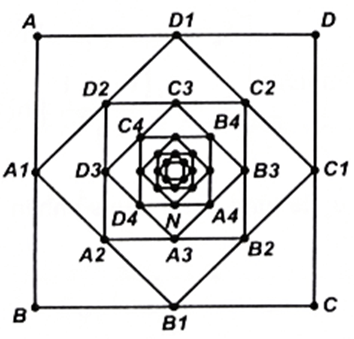
Ví dụ 3. Cho hình vuông C1 có cạnh bằng 1, C2 là hình vuông có các đỉnh là các trung điểm của cạnh hình vuông C1. Tương tự, gọi C3 là hình vuông có các đỉnh là trung điểm của các cạnh hình vuông C2. Tiếp tục như vậy ta được một dãy các hình vuông C1, C2, C3,..., Cn,... Tính tổng diện tích của 10 hình vuông đầu tiên của dãy.
Hướng dẫn giải
Diện tích của hình vuông C1 là 1.
Hình vuông C2 có cạnh bằng đường chéo hình vuông C1 là .
=> Diện tích của hình vuông C2 là .
Hình vuông C3 có cạnh bằng đường chéo hình vuông C2 là .
=> Diện tích của hình vuông C3 là .
Hình vuông Cn có cạnh bằng đường chéo hình vuông Cn-1 là .
=> Diện tích của hình vuông Cn là .
Do đó, dãy diện các hình vuông C1, C2, C3,..., Cn,... lập thành cấp số nhân với số hạng đầu
=> .
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Cho cấp số nhân (un) có . Số hạng thứ 17 là
A. .
B. .
C. .
D. .
Câu 2. Ba số 2x, 3x + 3,5x + 5 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Biết x ≠ -1, số hạng tiếp theo của cấp số nhân đó là
A. .
B. .
C. 250.
D. -250.
Câu 3. Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các số x, 2y, 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm q.
A. .
B. .
C. .
D. q = -3.
Câu 4. Tính x theo a, b, c nếu ba số x + a; x + b; x + c lập thành cấp số nhân.
A. .
B. .
C. .
D. .
Câu 5. Cho cấp số nhân (un) biết . Giá trị u1 và q là
A. u1 = 2; q = 5 hoặc u1 = 25 q = .
B. u1 = 5; q = 1 hoặc u1 = 25 q = .
C. u1 = 25; q = 5 hoặc u1 = 1 q = .
D. u1 = 1; q = 5 hoặc u1 = 25 q = .
Câu 6. Cho cấp số nhân có công bội q > 1 và . Tổng 10 số hạng đầu tiên của cấp số nhân là
A. .
B. .
C. .
D. .
Câu 7. Cho hệ phương trình . Có bao nhiêu giá trị dương của A để x, y, z lập thành một cấp số nhân.
A. 1.
B. 2.
C. 3.
D. 4.
Câu 8. Ba số a, b, c theo thứ tự là số hạng thứ nhất, số hạng thứ hai và số hạng thứ ba của một cấp số nhân, đồng thời cũng lần lượt là số hạng thứ nhất, số hạng thứ hai và số hạng thứ tư của một cấp số cộng có công sai bằng 10. Tìm a.
A. a = 5.
B. a = .
C. a = 10.
D. a = .
Câu 9. Cho ba số lập thành một cấp số nhân, với . Khi đó giá trị cos2α là
A. .
B. .
C. .
D. .
Câu 10. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mồi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 12288m2). Tính diện tích mặt trên cùng.
A. 8 m2.
B. 6 m2.
C. 12 m2.
D. 10 m2.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Cho cấp số nhân với . Xác định giá trị u1 của cấp số nhân.
|
Điền đáp án |
|
Câu 17. Bốn số a, b, c, d theo thứ tự lập thành một cấp số cộng và bốn số a + 1, b + 1, c + 3, d + 9 theo thứ tự lập thành một cấp số nhân. Tính a + d.
|
Điền đáp án |
|
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Cho cấp số nhân (un) với công bội q < 0 và u2 = 4, u4 = 9.
a) Số hạng đầu .
b) Số hạng .
c) là số hạng thứ 8.
d) Tổng 5 số hạng đầu của cấp số nhân là .
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Ứng dụng cấp số cộng - cấp số nhân vào thực tế
I. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán 1: Lãi đơn
1.1. Phương pháp giải
Khách hàng gửi vào ngân hàng A đồng với lãi đơn r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ ℕ*) là: .
1.2. Ví dụ
Ví dụ 1. Tính theo phương thức lãi đơn, để sau 2,5 năm rút được cả vốn lẫn lãi số tiền là 10892000 đồng với lãi suất một quý thì bạn phải gửi tiết kiệm số tiền bao nhiêu?
A. 9 336 000.
B. 10 456 000.
C. 617 000.
D. 2 108 000.
Hướng dẫn giải
Đây là bài toán lãi đơn với chu kỳ là một quý.
Vậy 2,5 năm ứng với 10 chu kỳ.
Với x là số tiền gửi tiết kiệm, ta có: => x = 9336000. Chọn A.
Ví dụ 2. Bạn Lan gửi 1500 USD với lãi suất đơn cố định theo quý. Sau 3 năm, số tiền bạn ấy nhận được cả gốc lẫn lãi là 2320 USD. Hỏi lãi suất tiết kiệm là bao nhiêu một quý? (làm tròn đến hàng phần nghìn).
A. 0,182.
B. 0,046.
C. 0,015.
D. 0,037.
Hướng dẫn giải
Đây là bài toán lãi đơn, chu kỳ là một quý. Áp dụng công thức, ta có: 2320 = 1500(1 + 12r%) bấm máy tính ta được lãi suất là r% ≈ 0,046 một quý. Chọn B.
2. Dạng toán 2: Lãi kép
2.1. Phương pháp giải
Khách hàng gửi vào ngân hàng A đồng với lãi kép r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ ℕ*) là: .
2.2. Ví dụ
Ví dụ 1. Bà Mai gửi tiết kiệm ngân hàng Vietcombank số tiền 50 triệu đồng với lãi suất 0,79% một tháng, theo phương thức lãi kép. Tính số tiền cả vốn lẫn lãi bà Mai nhận được sau 2 năm?
A. 60 393 000 đồng.
B. 50 793 000 đồng.
C. 50 790 000 đồng.
D. 59 480 000 đồng.
Hướng dẫn giải
Đây là bài toán lãi kép với chu kỳ là một tháng, ta áp dụng công thức A(1 + r)n với A = 50 triệu đồng, r% = 0,79% và n = 2.12 = 24 tháng.
Số tiền bà Mai nhận được sau 2 năm là: (triệu đồng) = 60 393 000 (đồng).
Chọn A.
Ví dụ 2. Chị Thanh gửi ngân hàng 155 triệu đồng, với lãi suất 1,02% một quý. Hỏi sau một năm số tiền lãi chị nhận được là bao nhiêu?
A. 161 421 000 đồng.
B. 6 324 000 đồng.
C. 1 581 000 đồng.
D. 6 421 000 đồng.
Hướng dẫn giải
Số tiền lãi chính là tổng số tiền cả gốc lẫn lãi trừ đi số tiền gốc, nên ta có tiền lãi là
(triệu đồng) = 6 421 000 (đồng). Chọn D.
3. Dạng toán 3: Gửi tiết kiệm hàng tháng
3.1. Phương pháp giải
Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi kép r% / tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng (n ∈ ℕ*) (nhận tiền cuối tháng, khi ngân hàng đã tính lãi) là Sn. Từ đó ta có công thức tổng quát .
3.2. Ví dụ
Ví dụ 1. Đầu mỗi tháng ông Mạnh gửi ngân hàng 580 000 đồng với lãi suất 0,7%/ tháng. Sau 10 tháng thì số tiền ông Mạnh nhận được cả gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu?
Hướng dẫn giải
Sau 10 tháng thì số tiền cả gốc và lãi mà ông Mạnh nhận được là:
Ví dụ 2. Đầu mỗi tháng thầy Quân gửi ngân hàng 3 000 000 đồng với lãi suất 0,6% / tháng. Hỏi ít nhất sau bao nhiêu tháng thì thầy Quân thu được số tiền cả gốc và lãi trên 100 triệu đồng?
Hướng dẫn giải
Số tiền cả gốc và lãi mà thầy Quân nhận được sau n tháng là:
Vậy sau ít nhất 31 tháng thì thầy Quân sẽ thu được cả gốc và lãi là trên 100 triệu đồng.
4. Dạng toán 4: Vay trả góp
4.1. Phương pháp giải
Vay từ ngân hàng số tiền A đồng với lãi kép r%/tháng. Sau đúng 1 tháng kể từ ngày vay bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng 1 tháng, số tiền hoàn nợ là a đồng. Từ đó số tiền cần trả hàng tháng để sau n tháng hết nợ là: .
4.2. Ví dụ
Ví dụ 1. Chị Minh vay số tiền 50 triệu đồng với lãi suất là 1,15%/tháng trong vòng 4 năm. Hỏi hàng tháng chị Minh phải trả góp với số tiền bao nhiêu để sau 4 năm thì hết nợ.
Hướng dẫn giải
Áp dụng công thức vay trả góp ta có: = .
Vậy hàng tháng chị Minh phải trả góp số tiền là 1,36 triệu đồng thì sau 4 năm sẽ hết nợ.
5. Dạng toán 5: Một số dạng toán thực tế khác
5.1. Phương pháp giải
Vận dụng linh hoạt các công thức đã học của cấp số cộng và cấp số nhân để thực hiện giải toán.
5.2. Ví dụ
Ví dụ 1. Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64 000 con hỏi sau bao nhiêu phút thì có được 2 048 000 con.
A. 10.
B. 11.
C. 26.
D. 50.
Hướng dẫn giải
Số lượng vi khuẩn tăng lên là cấp số nhân (un) với công bội q = 2.
Ta có u6 = 64000 => u1.q5 = 64000 => u1 = 2000.
Sau n phút thì số lượng vi khuẩn là un+1.
un+1 = 2048000 => u1.qn = 2048000 => 2000.2n = 2048000 => n = 10.
Vậy sau 10 phút thì có được 2 048 000 con. Chọn A.
Ví dụ 2. Một du khách vào chuồng đua ngựa đặt cược theo tỉ lệ đặt 1 ăn 2 (nghĩa là đặt 10 000 đồng thì khi thắng số tiền thu về là 20 000 đồng), lần đầu đặt 20 000 đồng, mỗi lần sau tiền đặt gấp đôi số tiền lần đặt trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khách trên thắng hay thua bao nhiêu tiền?
A. Hòa vốn.
B. Thua 20 000 đồng.
C. Thắng 20 000 đồng.
D. Thua 40 000 đồng.
Hướng dẫn giải
Số tiền đặt cược cho mỗi lần của du khách là một cấp số nhân (un) với u1 = 20 000 và công bội q = 2.
Số tiền đặt cược ở lần thứ 10 là u10 = u1.q9.
Số tiền du khách này thắng ở lần đặt cược thứ 10 là: 2u10.
Tổng số tiền du khách này tham gia trong 10 lần đặt cược là: .
Sau 10 lần đặt cược số tiền người này thu được là:
.
Vậy cuối cùng người du khách đó thắng được số tiền là 20 000 đồng. Chọn C.
II. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Dân số thế giới cuối năm 2010, ước tính 7 tỉ người. Hỏi với mức tăng trưởng dân số 1,5% mỗi năm thì cuối năm 2020 dân số thế giới là bao nhiêu?
A. 8,12 tỉ người.
B. 8,05 tỉ người.
C. 8 tỉ người.
D. 8,10 tỉ người.
Câu 2. Giả sử cứ sau một năm diện tích rừng của nước ta giảm x phần trăm diện tích hiện có. Hỏi sau 4 năm diện tích rừng của nước ta sẽ là bao nhiêu lần diện tích hiện nay?
A. .
B. .
C. .
D. .
Câu 3. Một bể nước có dung tích 1000 lít. Người ta mở vòi cho nước chảy vào bể, ban đầu bể cạn nước. Trong giờ đầu vận tốc nước chảy vào bể là 1 lít/1phút. Trong các giờ tiếp theo vận tốc nước chảy giờ sau gấp đôi giờ liền trước. Hỏi sau khoảng thời gian bao lâu thì bể đầy nước (kết quả gần đúng nhất).
A. 3,14 giờ.
B. 4,64 giờ.
C. 4,14 giờ.
D. 3,64 giờ.
Câu 4. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá của mét khoan đầu tiên là 80 000 đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng thêm 5 000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50 m mới có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
A. 10 125 000 đồng.
B. 52 500 000 đồng.
C. 52 500 000 đồng.
D. 4 000 000 đồng.
Câu 5. Trong tháng 12, lớp 11A dự kiến quyên góp tiền để đi làm từ thiện như sau: ngày đầu tiên quyên góp, mỗi bạn bỏ 2000 đồng vào lợn, từ ngày thứ hai trở đi mỗi bạn bỏ vào lợn hơn ngày liền trước đó 500 đồng. Hỏi sau 28 ngày lớp 11A quyên góp được bao nhiêu tiền? Biết lớp có 40 bạn.
A. 8 800 000 đồng.
B. 9 800 000 đồng.
C. 10 800 000 đồng.
D. 10 800 000 đồng.
Câu 6. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đối một lần. Giả sử 1 tế bào E. Coli khối lượng khoảng 15 ∙ 10-15g. Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là bao nhiêu? (chọn đáp án chính xác nhất).
A. 2,34 ∙ 1029 (g).
B. 3,36 ∙ 1029 (g).
C. 2,25 ∙ 1026 (kg).
D. 3,35 ∙ 1026 (kg).
Câu 7. Tính đến đầu năm 2011, dân số toàn tỉnh Bình Phước đạt gần 905 300, mức tăng dân số là 1,37% mỗi năm. Tỉnh thực hiện tốt chủ trương 100% trẻ em đúng độ tuổi đều vào lớp 1. Đến năm học 2024-2025 ngành giáo dục của tỉnh cần chuẩn bị bao nhiêu phòng học cho học sinh lớp 1, mỗi phòng dành cho 35 học sinh? (Giả sử trong năm sinh của lứa học sinh vào lớp 1 đó toàn tỉnh có 2 400 người chết, số trẻ tử vong trước 6 tuổi không đáng kể)
A. 458.
B. 222.
C. 459.
D. 221.
Câu 8. Ông An bắt đầu đi làm với mức lương khởi điểm là 1 triệu đồng một tháng. Cứ sau 3 năm thì ông An được tăng lương 40%. Hỏi sau tròn 20 năm đi làm tổng tiền lương ông An nhận được là bao nhiêu (làm tròn đến hai chữ số thập phân sau dấu phẩy)?
A. 726,74 triệu đồng.
B. 71674 triệu đồng.
C. 858,72 triệu đồng.
D. 768,37 triệu đồng.
Câu 9. Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định trong khoảng thời gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả gần đúng đến hàng phần trăm)
A. 215,10 triệu đồng.
B. 214,90 triệu đồng.
C. 224,10 triệu đồng.
D. 234,90 triệu đồng.
Câu 10. Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4 000 000 đồng vào một ngày cố định của tháng ở ngân hàng M với lãi suất không thay đổi trong suốt thời gian gửi tiền là 0,6% tháng. Gọi A đồng là số tiền người đó có được sau 25 năm. Hỏi mệnh đề nào dưới đây là đúng?
A. 3 450 000 000 < A < 3 500 000 000.
B. 3 500 000 000 < A < 3 550 000 000.
C. 3 400 000 000 < A < 3 450 000 000.
D. 3 350 000 000 < A < 3 400 000 000.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
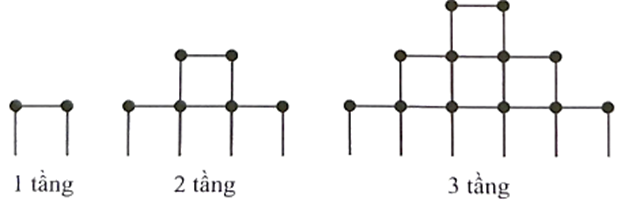
Câu 16. Bạn An chơi trò chơi xếp các que diêm thành tháp theo quy tắc thể hiện như hình vẽ. Để xếp được tháp có 10 tầng thì bạn An cần đúng bao nhiêu que diêm?
|
Điền đáp án |
|
Câu 17. Trên bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt vào ô thứ hai số hạt dẻ nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt dẻ nhiều hơn ô thứ hai là 5, ... và cứ thế tiếp tục đến ô thứ n. Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng 25 450 hạt dẻ. Hỏi bàn cờ có bao nhiêu ô?
|
Điền đáp án |
|
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Cho tứ giác ABCD có bốn góc tạo thành một cấp số nhân có công bội bằng 2.
a) Số đo góc nhỏ nhất bằng 24°.
b) Số đo góc lớn nhất bằng 196°.
c) Tổng số đo góc lớn nhất với góc nhỏ nhất bằng 220°.
d) Số đo góc lớn nhất trừ cho số đo góc nhỏ nhất bằng 168°.
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Tập hợp
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đại số tổ hợp
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đường tròn trong mặt phẳng tọa độ
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Hàm số lượng giác và phương trình lượng giác
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Giới hạn. Hàm số liên tục
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Lũy thừa - Mũ - Logarit
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

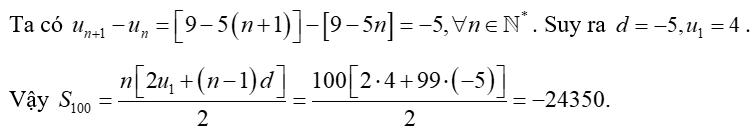
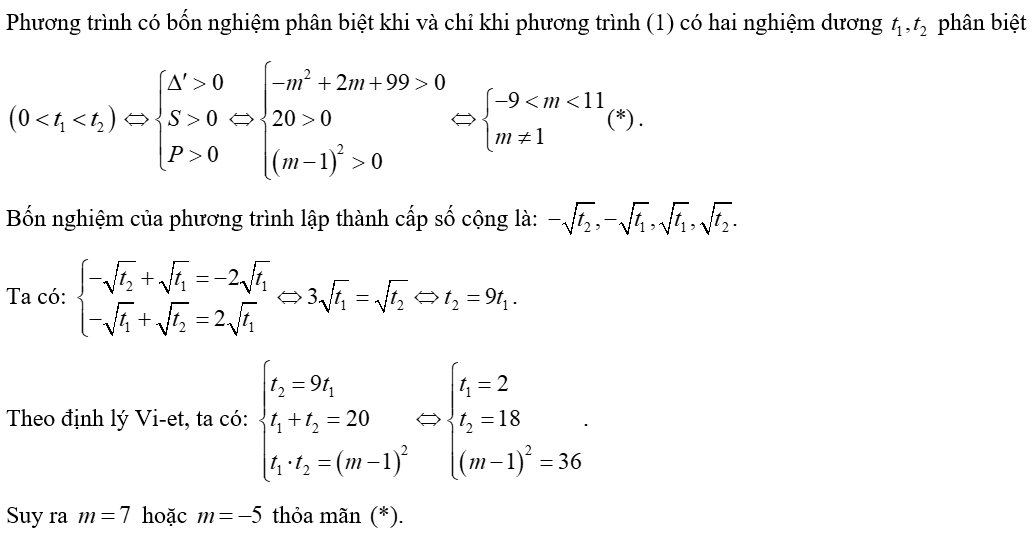
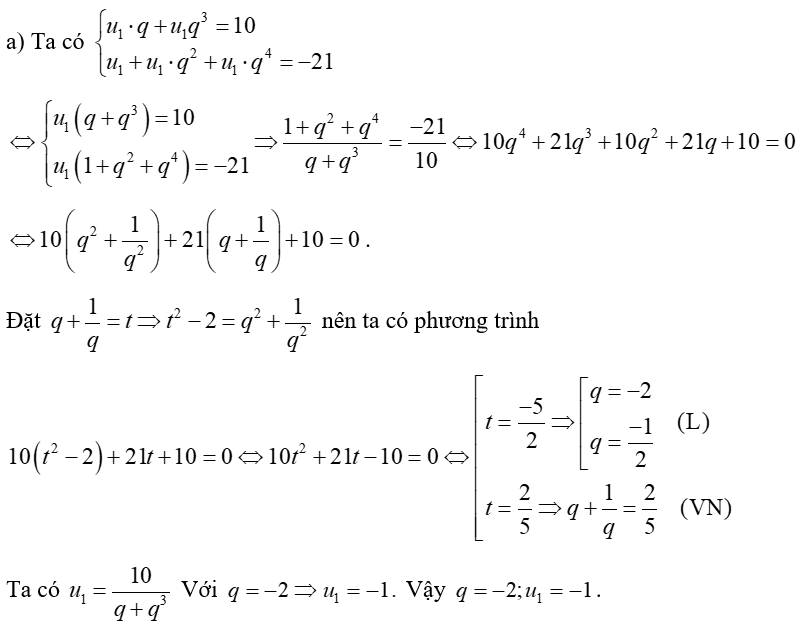
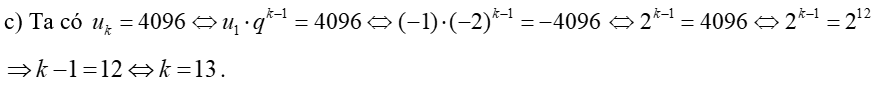
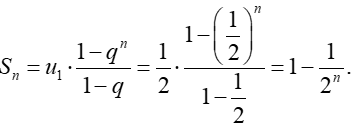
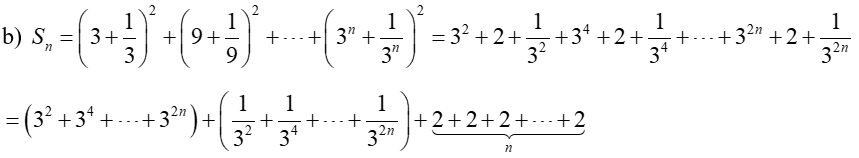

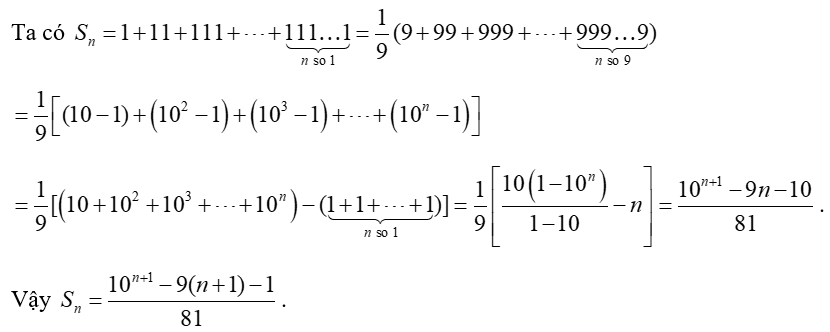
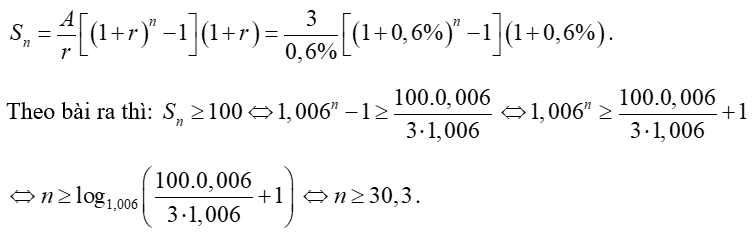



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

