(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đại số tổ hợp
Chuyên đề Đại số tổ hợp trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đại số tổ hợp
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
(Ôn thi ĐGNL, ĐGTD) Quy tắc đếm
I. LÝ THUYẾT CẦN NHỚ
1. Quy tắc cộng
• Giả sử một công việc nào đó có thể thực hiện theo một trong hai phương án khác nhau:
Phương án 1 có n1 cách thực hiện.
Phương án 2 có n2 cách thực hiện.
Khi đó số cách thực hiện công việc là: n1 + n2 cách.
|
Công việc A |
Phương án 1: n1 cách |
Tổng số cách = n1 + n2 |
|
Phương án 2: n2 cách |
• Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau:
Nếu A và B là các tập hợp hữu hạn không giao nhau thì .
• Mở rộng: Một công việc được hoàn thành bởi một trong k hành động . Nếu hành động A1 có m1 cách thực hiện, hành động A2 có m2 cách thực hiện, ..., hành động Ak có mk cách thực hiện và các cách thực hiện của các hành động trên không trùng nhau thì công việc đó có cách thực hiện.
2. Quy tắc nhân
• Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai.
Khi đó công việc đó có m.n cách thực hiện.
• Mở rộng: Một công việc được hoàn thành bởi k hành động liên tiếp. Nếu hành động A1 có m1 cách thực hiện, ứng với mỗi cách thực hiện hành động A1 có m2 cách thực hiện hành động A2, …, có mk cách thực hiện hành động Ak, thì công việc đó có cách hoàn thành.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Ứng dụng quy tắc cộng
1.1. Phương pháp giải
Để đếm số cách lựa chọn để thực hiện một công việc A bằng quy tắc cộng, ta thực hiện các bước như sau:
Bước 1: Phân tích xem có bao nhiêu phương án riêng biệt để thực hiện công việc A (có nghĩa công việc A có thể hoàn thành một trong các phương án ).
Bước 2: Đếm số cách chọn trong các phương án .
Bước 3: Dùng quy tắc cộng ta tính được số cách lựa chọn để thực hiện công việc A là:
.
1.2. Ví dụ
Ví dụ 1. Một người có 4 cái quần khác nhau, 6 cái áo khác nhau, 3 chiếc cà vạt khác nhau. Hỏi có bao nhiêu cách chọn một cái quần hoặc một cái áo hoặc một cái cà vạt?
|
Điền đáp án |
|
Hướng dẫn giải
Nếu chọn một cái quần thì sẽ có 4 cách.
Nếu chọn một cái áo thì sẽ có 6 cách.
Nếu chọn một cái cà vạt thì sẽ có 3 cách.
Theo quy tắc cộng, ta có 4 + 6 + 3 = 13 cách chọn.
Điền đáp án: 13.
Ví dụ 2. Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hóa. Mỗi thí sinh được quyền chọn một đề tài. Hỏi mỗi thí sinh có bao nhiêu khả năng lựa chọn đề tài?
A. 20.
B. 3360.
C. 31.
D. 30.
Hướng dẫn giải
Nếu chọn đề tài về lịch sử có 8 cách.
Nếu chọn đề tài về thiên nhiên có 7 cách.
Nếu chọn đề tài về con người có 10 cách.
Nếu chọn đề tài về văn hóa có 6 cách.
Theo quy tắc cộng, ta có 8 + 7 + 10 + 6 = 31 cách chọn. Chọn C.
Ví dụ 3. Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần?
A. 5.
B. 15.
C. 55.
D. 10.
Hướng dẫn giải
Vì số có chín chữ số viết theo thứ tự giảm dần nên chỉ có thể là chữ số 9 hoặc chữ số 8 đứng đầu.
Trường hợp 1: số 9 đứng đầu.
Từ các số 0; 1; 2; 3; 4; 5; 6; 7; 8 mỗi một lần ta bỏ đi một số ta sẽ lập được 1 số có 9 chữ số viết theo thứ tự giảm dần mà số 9 đứng đầu.
Vậy trường hợp 1 có 9 số được lập.
Trường hợp 2: số 8 đứng đầu.
Vì từ 0 đến 8 có chín chữ số nên ta chỉ lập được 1 số có 9 chữ số viết theo thứ tự giảm đần.
Vậy cả 2 trường hợp có 9 + 1 = 10 số. Chọn D.
2. Dạng toán: Ứng dụng quy tắc nhân
2.1. Phương pháp giải
Để đếm số cách lựa chọn để thực hiện công việc A bằng quy tắc nhân, ta thực hiện các bước sau:
Bước 1: Phân tích xem có bao nhiêu công đoạn liên tiếp cần phải tiến hành để thực hiện công việc A (giả sử A chỉ hoàn thành sau khi tất cả các công đoạn hoàn thành).
Bước 2: Đếm số cách chọn trong các công đoạn .
Bước 3: Dùng quy tắc nhân ta tính được số cách lựa chọn để thực hiện công việc A là:
.
Ta thường gặp một số bài toán sau:
! Bài toán 1: Đếm số phương án liên quan đến số.
Khi lập một số tự nhiên ta cần lưu ý:
* và .
* x là số chẵn ⇔ an là số chẵn.
* x là số lẻ ⇔ an là số lẻ.
* x chia hết cho 3 ⇔ chia hết cho 3.
* x chia hết cho chia hết cho 4.
* x chia hết cho .
* x chia hết cho 6 ⇔ x là số chẵn và chia hết cho 3.
* x chia hết cho chia hết cho 8.
* x chia hết cho chia hết cho 9.
* x chia hết cho 11 ⇔ tổng các chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số nguyên chia hết cho 11.
* x chia hết cho 25 ⇔ hai chữ số tận cùng là 00, 25, 50, 75.
! Bài toán 2: Đếm số phương án liên quan đến kiến thức thực tế.
! Bài toán 3: Đếm số phương án liên quan đến hình học.
2.2. Ví dụ
Ví dụ 1. Một đội học sinh giỏi của trường THPT, gồm 5 học sinh khối 12; 4 học sinh khối 11; 3 học sinh khối 10. Số cách chọn ba học sinh trong đó mỗi khối có một em?
A. 12.
B. 220.
C. 60.
D. 3.
Hướng dẫn giải
Để chọn ba học sinh trong đó mỗi khối có một em, ta có:
• Có 5 cách chọn học sinh khối 12.
• Có 4 cách chọn học sinh khối 11.
• Có 3 cách chọn học sinh khối 10.
Vậy theo quy tắc nhân ta có: 5.4.3 = 60 cách. Chọn C.
Ví dụ 2. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
|
Điền đáp án |
|
Hướng dẫn giải
• Từ A → B có 4 cách.
• Từ B → C có 2 cách.
• Từ C → D có 3 cách.
Vậy theo quy tắc nhân ta có 4.2.3 = 24 cách.
Điền đáp án: 24.
Ví dụ 3. Biển số xe máy của tỉnh A có 6 kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái tiếng Anh, kí tự ở vị trí thứ hai là một chữ số thuộc tập {1;2;3;...;9}, mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập {0;1;2;3;...;9}. Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh A có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau?
A. 2 340 000.
B. 234 000.
C. 75.
D. 2 600 000.
Hướng dẫn giải
Giả sử biển số xe là a1a2a3a4a5a6.
• Có 26 cách chọn a1 (do có 26 chữ cái trong bảng chữ cái tiếng Anh).
• Có 9 cách chọn a2.
• Có 10 cách chọn a3.
• Có 10 cách chọn a4.
• Có 10 cách chọn a5.
• Có 10 cách chọn a6.
Vậy theo quy tắc nhân ta có 26.9.104 = 2340000 biển số xe. Chọn A.
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Một trường THPT được cử một học sinh đi dự trại hè toàn quốc. Nhà trường quyết định chọn một học sinh tiên tiến lớp 11A hoặc lớp 12B. Hỏi nhà trường có bao nhiêu cách chọn, nếu biết rằng lớp 11A có 31 học sinh tiên tiến và lớp 12B có 22 học sinh tiên tiến?
A. 31.
B. 9.
C. 53.
D. 682.
Câu 2. Giả sử từ tỉnh A đến tỉnh B có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa, 3 chuyến tàu thủy và 2 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh B?
A. 20.
B. 300.
C. 18.
D. 15.
Câu 3. Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là
A. 480.
B. 24.
C. 48.
D. 60.
Câu 4. Một người có 4 cái quần, 6 cái áo, 3 chiếc cà vạt. Để chọn mỗi thứ một món thì có bao nhiêu cách chọn bộ “quần - áo - cà vạt” khác nhau?
A. 13.
B. 72.
C. 12.
D. 30.
Câu 5. Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn hai học sinh trong đó có một nam và một nữ đi dự trại hè của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 910000.
B. 91000.
C. 910.
D. 625.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Một hộp chứa 16 quả cầu gồm sáu quả cầu xanh đánh số từ 1 đến 6, năm quả cầu đỏ đánh số từ 1 đến 5 và năm quả cầu vàng đánh số từ 1 đến 5. Hỏi có bao nhiêu cách lấy ra từ hộp đó 3 quả cầu vừa khác màu vừa khác số.
|
Điền đáp án |
|
Câu 17. Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện: sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
|
Điền đáp án |
|
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 19. Xếp 6 người A, B, C, D, E, F vào một ghế dài. Ta sẽ có số cách sắp xếp
a) A và F ngồi ở hai đầu ghế là 48 cách.
b) A và F ngồi cạnh nhau là 120 cách.
c) A và F không ngồi cạnh nhau là 240 cách.
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Hoán vị, chỉnh hợp, tổ hợp
I. LÝ THUYẾT CẦN NHỚ
1. Hoán vị
Cho tập hợp A có n phần tử (n ≥ 1).
Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một hoán vị các phần tử đó (gọi tắt là hoán vị của A hay của n phần tử).
Kí hiệu Pn là số hoán vị của n phần tử.
Người ta chứng minh được rằng: Số các hoán vị của n phần tử (n ≥ 1) bằng
Pn = n.(n - 1).(n - 2)....2.1.
Chú ý:
+ Kí hiệu và đọc là n giai thừa hoặc giai thừa của n. Khi đó, Pn = n!.
+ Quy ước: 0! = 1.
+ Nếu bài toán sắp xếp n người (vật) theo vòng tròn, có nghĩa phần tử đầu tiên và phần tử cuối cùng trùng nhau. Vậy ta sẽ có đây là hoán vị của (n - 1) phần tử, khi đó, số cách sắp xếp là (n - 1)!.
2. Chỉnh hợp
Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k với 1 ≤ k ≤ n.
Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.
Kí hiệu là số chỉnh hợp chập k của n phần tử.
Người ta chứng minh được rằng: Số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n bằng
.
Nhận xét: Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó. Ta có .
3. Tổ hợp
Cho tập hợp A có n phần tử (n ≥ 1).
Mỗi tập con gồm k phần tử1 ≤ k ≤ n của A được gọi là một tổ hợp chập k của n phần tử.
Kí hiệu là số tổ hợp chập k của n phần tử (1 ≤ k ≤ n).
Người ta chứng minh được rằng: Số các tổ hợp chập k của n phần tử (1 ≤ k ≤ n) bằng
.
Chú ý:
+ Người ta quy ước .
+ Khác với chỉnh hợp, trong tổ hợp k phần tử đang xét không có yếu tố thứ tự.
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Bài toán chỉ sử dụng hoán vị (hoặc chỉnh hợp hoặc tổ hợp)
1.1. Phương pháp giải
Bước 1: Phân biệt rõ bài toán sử dụng hoán vị, chỉnh hợp, hay tổ hợp dựa vào định nghĩa.
Bước 2: Xét các trường hợp của bài toán, tính riêng từng cách chọn (có thể áp dụng quy tắc đếm).
Bước 3: Thay giá trị theo công thức tính số các hoán vị, chỉnh hợp, tổ hợp và sử dụng máy tính đưa ra kết quả.
1.2. Ví dụ
Dạng 1. Chỉ sử dụng hoán vị
Ví dụ 1. Cho A = {1; 2; 3; 4}. Từ A lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau?
A. 32.
B. 24.
C. 256.
D. 1.
Hướng dẫn giải
Mỗi số tự nhiên tự nhiên có 4 chữ số khác nhau được lập từ tập A là hoán vị của 4 phần tử.
Vậy có 4! = 24 số cần tìm. Chọn B.
Ví dụ 2. Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5! ∙ 8!.
B. 5! ∙ 7!.
C. 2 ∙ 5! ∙ 7!.
D. 12!.
Hướng dẫn giải
Vì các sách Văn phải xếp kề nhau nên ta xem 5 cuốn sách Văn là một phần tử.
Xếp 7 cuốn sách toán lên kệ có 7! cách.
Giữa 7 cuốn sách Toán có 8 khoảng trống, ta xếp phần tử chứa 5 cuốn sách Văn vào 8 vị trí đó có 8 cách.
5 cuốn sách Văn có thể hoán đổi vị trí cho nhau ta được 5! cách.
Vậy số cách sắp xếp thỏa mãn yêu cầu bài toán là: 8 ∙ 7! ∙ 5! = 8! ∙ 5!. Chọn A.
Ví dụ 3. Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
A. 6.
B. 144.
C. 720.
D. 72.
Hướng dẫn giải
Đánh số thứ tự các vị trí theo hàng dọc từ 1 đến 6.
Trường hợp 1: Nam đứng trước, nữ đứng sau.
• Xếp nam (vào các vị trí đánh số 1, 3, 5): Có 3! = 6 cách.
• Xếp nữ (vào các vị trí đánh số 2, 4, 6): Có 3! = 6 cách.
Vậy trường hợp này có: 6 ∙ 6 = 36 cách.
Trường hợp 2: Nữ đứng trước, nam đứng sau.
• Xếp nữ (vào các vị trí đánh số 1, 3, 5): Có 3! = 6 cách.
• Xếp nam (vào các vị trí đánh số 2, 4, 6): Có 3! = 6 cách.
Vậy trường hợp này có: 6 ∙ 6 = 36 cách.
Theo quy tắc cộng ta có: 36 + 36 = 72 cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ. Chọn D.
Dạng 2. Chỉ sử dụng chỉnh hợp
Ví dụ 1. Cho tập A = {1; 2; 3; 5; 7; 9}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số đôi một khác nhau?
A. 720.
B. 360.
C. 120.
D. 24.
Hướng dẫn giải
Tập A gồm có 6 phần tử là những số tự nhiên khác 0.
Từ tập A có thể lập được số tự nhiên gồm bốn chữ số đôi một khác nhau. Chọn B.
Ví dụ 2. Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số khác nhau.
A. 500.
B. 405.
C. 360.
D. 328.
Hướng dẫn giải
Xét hai trường hợp.
TH1: Chữ số tận cùng là 0 có 1 cách chọn chữ số tận cùng.
Có cách chọn hai chữ số đầu.
Do đó có 1 ∙ = 72 số.
TH2: Chữ số tận cùng là 2, 4, 6, 8 có 4 cách chọn chữ số tận cùng.
Có 8 cách chọn chữ số đầu tiên.
Có 8 cách chọn chữ số ở giữa.
Do đó có 4 ∙ 8 ∙ 8 = 256 số.
Vậy có 72 + 256 = 328 số thỏa mãn bài toán. Chọn D.
Ví dụ 3. Từ các chữ số của tập hợp {0; 1; 2; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau mà trong đó nhất thiết phải có mặt chữ số 0?
A. 504.
B. 480.
C. 720.
D. 120.
Hướng dẫn giải
Cách 1: Gọi số cần tìm là .
Có 4 vị trí xếp số 0 vì a ≠ 0.
a, b, c, d được chọn trong 5 số còn lại và sắp, có cách.
Vậy số các số cần tìm 4 ∙ 120 = 480.
Cách 2: Gọi số cần tìm là .
Có 5 vị trí xếp số 0 (kể cả vị trí đầu tiên), 4 vị trí còn lại chọn 4 trong 5 số và sắp, nên có số.
Các số có dạng là số.
Vậy số các số cần tìm là 600 –120 = 480. Chọn B.
Dạng 3. Chỉ sử dụng tổ hợp
Ví dụ 1. Trong hộp có 5 quả cầu đỏ và 7 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 5 quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.
A. 245.
B. 3 480.
C. 246.
D. 3 360.
Hướng dẫn giải
Lấy ngẫu nhiên 5 quả cầu từ hộp 12 quả cầu, để số quả cầu đỏ nhiều hơn số quả cầu xanh, những trường hợp có thể xảy ra là
Trường hợp 1: 5 cầu đỏ. Số khả năng: = 1 khả năng.
Trường hợp 2: 4 cầu đỏ, 1 cầu xanh. Số khả năng: = 35 khả năng.
Trường hợp 3: 3 cầu đỏ, 2 cầu xanh. Số khả năng: = 210 khả năng.
Áp dụng quy tắc cộng: có tất cả: 35 + 210 + 1 = 246 khả năng. Chọn C.
Ví dụ 2. Cho đa giác đều 36 đỉnh. Hỏi có bao nhiêu hình chữ nhật có đỉnh là 4 trong 36 đỉnh của đa giác đều?
A. 306.
B. 153.
C. 9.
D. 58 905.
Hướng dẫn giải
Do đa giác đều 36 đỉnh có 18 đường chéo qua tâm.
Mặt khác cứ 2 đường chéo qua tâm ứng với một hình chữ nhật có 4 đỉnh là đỉnh của đa giác.
Vậy số hình chữ nhật là = 153. Chọn B.
Bài toán tổng quát:
Do đa giác đều 2n (n ∈ ℕ, n ≥ 2) đỉnh có n đường chéo qua tâm.
Mặt khác cứ 2 đường chéo qua tâm ứng với một hình chữ nhật có 4 đỉnh là đỉnh của đa giác.
Vậy số hình chữ nhật là .
Ví dụ 3. Có 10 đội bóng thi đấu theo thể thức vòng tròn một lượt, thắng được điểm, hòa 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng cộng số điểm của tất cả 10 đội là 130. Hỏi có bao nhiêu trận hòa?
A. 7.
B. 8.
C. 5.
D. 6.
Hướng dẫn giải
Vì 10 đội bóng thi đấu theo thể thức vòng tròn một lượt nên số trận đấu là = 45 (trận).
Gọi số trận hòa là x, số không hòa là 45 − x (trận).
Tổng số điểm mỗi trận hòa là 2, tổng số điểm của trận không hòa là 3(45 − x).
Theo đề bài ta có phương trình 2x + 3(45 − x) =130, suy ra x = 5.
Vậy có 5 trận hòa.
2. Dạng toán: Bài toán kết hợp hoán vị, tổ hợp, chỉnh hợp
2.1. Phương pháp giải
Thực hành với các bài toán độc lập để xác định rõ các trường hợp.
• Phân loại câu hỏi: Có sắp xếp thứ tự hay không, nếu có thì sắp xếp bao nhiêu phần tử.
• Xác định dạng toán: dạng toán chữ số, sắp xếp đồ vật, hình học, ...
Phân biệt hoán vị, chỉnh hợp, tổ hợp:
|
Câu hỏi phân loại |
Hoán vị |
Chỉnh hợp |
Tổ hợp |
|
1. Có sắp xếp thứ tự hay không? |
Có |
Có |
Không |
|
2. Số phần tử sắp xếp? |
Tất cả n phần tử |
Chỉ có k phần tử trong n |
|
2.2. Ví dụ
Ví dụ 1. Từ các chữ số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau trong đó luôn có mặt hai chữ số 1 và 6.
A. 408.
B. 720.
C. 480.
D. 120.
Hướng dẫn giải
Chọn 3 chữ số khác nhau từ các số trong tập hợp {2; 3; 4; 5}: có cách.
Sau đó, sắp xếp 5 chữ số đã chọn: có 5! cách.
Vậy có cả = 480 số có 5 chữ số khác nhau và luôn có mặt số 1 và số 6. Chọn C.
Ví dụ 2. Có bao nhiêu số tự nhiên có tám chữ số trong đó có ba chữ số 0, không có hai chữ số 0 nào đứng cạnh nhau và các chữ số khác chỉ xuất hiện nhiều nhất một lần.
A. 786 240.
B. 846 000.
C. 907 200.
D. 151 200.
Hướng dẫn giải
Chọn ra 5 chữ số khác 0 trong 9 chữ số (từ 1 đến 9) và sắp xếp chúng theo thứ tự có cách.
Để hai chữ số 0 không đứng cạnh nhau ta có 6 vị trí để xếp (do 5 chữ số vừa chọn tạo ra 6 vị trí).
Do chữ số 0 không thể xếp ở đầu nên còn 5 vị trí để xếp số 0.
Khi đó xếp 3 số 0 vào 5 vị trí nên có cách.
Vậy có = 151 200 số cần tìm. Chọn D.
Ví dụ 3. Có bao nhiêu cách chia hết 4 đồ vật khác nhau cho 3 người, biết rằng mỗi người nhận được ít nhất 1 đồ vật.
A. 36.
B. 3.
C. 12.
D. 72.
Hướng dẫn giải
Có hai người mà mỗi người nhận một đồ vật và một người nhận hai đồ vật.
Chọn hai người để mỗi người nhận một đồ vật: có cách chọn.
Chọn hai đồ vật trao cho hai người: có cách chọn.
Hai đồ vật còn lại trao cho người cuối cùng.
Vậy số cách chia là: = 36 cách. Chọn A.
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Mệnh đề nào đúng trong các mệnh đề sau?
A. .
B. .
C. .
D. .
Câu 2. Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có 4 giải: 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi có bao nhiêu kết quả có thể nếu biết rằng người giữ vé số 47 trúng một trong bốn giải?
A. 3 766 437.
B. 3 764 637.
C. 3 764 367.
D. 3 764 376.
Câu 3. Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
A. 249.
B. 7440.
C. 3204.
D. 2942.
Câu 4. Cho mặt phẳng chứa đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng 1 cạnh là cạnh của (H).
A. 1 440.
B. 360.
C. 1 120.
D. 816.
Câu 5. Cho 10 điểm phân biệt A1, A2, ..., A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
A. 96 tam giác.
B. 60 tam giác.
C. 116 tam giác.
D. 80 tam giác.
................................
................................
................................
Dạng 2. Câu trắc nghiệm trả lời ngắn
Câu 16. Một nhóm 6 bạn học sinh mua vé vào rạp chiếu phim. Các bạn mua 6 vé gồm 3 vé mang số ghế chẵn, 3 vé mang số ghế lẻ và không có hai vé nào cùng số. Trong sáu bạn thì hai bạn muốn ngồi bên ghế chẵn, hai bạn muốn ngồi bên ghế lẻ, hai bạn còn lại không có yêu cầu gì. Hỏi có bao nhiêu cách xếp chỗ để thỏa mãn các yêu cầu của tất cả các bạn đó?
|
Điền đáp án |
|
Câu 17. Có 4 cặp vợ chồng được xếp ngồi trên một chiếc ghế dài có 8 chỗ. Biết rằng mỗi người vợ chỉ ngồi cạnh chồng của mình hoặc ngồi cạnh một người phụ nữ khác. Hỏi có bao nhiêu cách sắp xếp chỗ ngồi thỏa mãn.
|
Điền đáp án |
|
................................
................................
................................
Dạng 3. Câu trắc nghiệm đúng sai
Trong mỗi ý a), b), c) ở mỗi câu, thi sinh chọn đúng hoặc sai.
Câu 19. Một câu lạc bộ cờ vua có 10 bạn nam và 7 bạn nữ. Huấn luyện viên muốn chọn 4 bạn đi thi đấu cờ vua.
a) Có 210 cách chọn 4 bạn nam đi thi.
b) Có 420 cách chọn 4 bạn không phân biệt nam, nữ.
c) Có 945 cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ.
................................
................................
................................
(Ôn thi ĐGNL, ĐGTD) Nhị thức newton
I. LÝ THUYẾT CẦN NHỚ
1. Công thức nhị thức Newton
• Công thức khai triển (a + b)n với n ∈ {4;5}:
• Mở rộng: Khai triển (a + b)n được cho bởi công thức sau:
Với a, b là các số thực và n là số nguyên dương, ta có
Quy ước a0 = b0 = 1.
Công thức trên được gọi là công thức nhị thức Newton (viết tắt là Nhị thức Newton).
Trong biểu thức ở VP của công thức (1):
+ Số các hạng tử là n + 1.
+ Số các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n.
+ Các hệ số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.
+ Số hạng thứ k (số hạng tổng quát) của khai triển là: .
Hệ quả:
Với a = b = 1, thì ta có .
Với a = 1; b = 1, ta có .
2. Một số dạng khai triển thường gặp
II. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
1. Dạng toán: Tiếp cận khai triển nhị thức Newton
1.1. Phương pháp giải
• Vận dụng công thức.
• Áp dụng hệ quả.
1.2. Ví dụ
Ví dụ 1. Viết khai triển theo công thức nhị thức Newton với biểu thức (x - y)5.
A. .
B. .
C. .
D. .
Lời giải
Ví dụ 2. Từ khai triển biểu thức (x + 1)10 thành đa thức. Tổng các hệ số của đa thức là:
A. 1 023.
B. 512.
C. 1 024.
D. 2 048.
Hướng dẫn giải
Xét khai triển .
Gọi S là tổng các hệ số trong khai triển thì ta có S = f(1) = . Chọn C.
2. Dạng toán: Tìm hệ số trong khai triển nhị thức Newton
2.1. Phương pháp giải
Áp dụng công thức khai triển:
Số hạng tổng quát của khai triển là: .
Hệ số là phần không chứa biến trong số hạng.
2.2. Ví dụ
Ví dụ 1. Hệ số lớn nhất trong khai triển là:
A. .
B. .
C. .
D. .
Hướng dẫn giải
Ví dụ 2. Biết hệ số của x2 trong khai triển của (1 - 3x)n là 90. Tìm n.
A. n = 7.
B. n = 6.
C. n = 8.
D. n = 5.
Hướng dẫn giải
Số hạng thứ k + 1 trong khai triển của (1 - 3x)n là: .
Số hạng chứa x2 ứng với k = 2.
Ta có: ⇔ ⇔ ⇔ n(n - 1) = 20 ⇔ .
Vậy n = 5. Chọn D.
Ví dụ 3. Tìm hệ số của x5 trong khai triển .
A. 1716.
B. 1715.
C. 1287.
D. 1711.
Hướng dẫn giải
Xét nhị thức có số hạng tổng quát là . Ta có:
Hệ số của x5 trong (1 + x)6 là .
Hệ số của x5 trong (1 + x)7 là .
Hệ số của x5 trong (1 + x)12 là .
Vậy hệ số của x5 trong khai triển P(x) là . Chọn B.
3. Dạng toán: Tìm số hạng trong khai triển nhị thức Newton
3.1. Phương pháp giải
Áp dụng công thức khai triển:
Số hạng tổng quát của khai triển là: .
3.2. Ví dụ
Ví dụ 1. Tìm số hạng không chứa x trong khai triển .
A. 10.
B. 20.
C. 5.
D. 1.
Hướng dẫn giải
Số hạng tổng quát trong khai triển là: .
Số hạng cần tìm không chứa x nên ta có: 10 - 5k = 0 ⇔ k = 2.
Vậy số hạng không chứa x trong khai triển là . Chọn A.
Ví dụ 2. Tìm số hạng chứa x3 trong khai triển .
A. .
B. .
C. .
D. .
Hướng dẫn giải
Số hạng thứ k + 1 trong khai triển là: .
Số hạng chứa x3 có giá trị k thỏa mãn: 9 - 2k = 3 ⇔ k = 3.
Vậy số hạng chứa x3 trong khai triển là: . Chọn A.
4. Dạng toán: Tính tổng của các tổ hợp và ứng dụng
4.1. Phương pháp giải
Sử dụng các hệ quả vào bài toán.
4.2. Ví dụ
Ví dụ 1. Tổng bằng
A. 2n - 1.
B. 2n - 1.
C. 2n.
D. 0.
Hướng dẫn giải
Theo khai triển nhị thức Newton .
Với a = b = 1, ta có . Chọn C.
Ví dụ 2. Với n ≥ 4, tổng bằng
A. 2n - 1.
B. 2n - 1.
C. 2n.
D. 2n - 1.
Hướng dẫn giải
Ví dụ 3. Cho n ∈ ℕ*, tính tổng .
|
Điền đáp án |
|
Hướng dẫn giải
5. Dạng toán: Dùng hai số hạng đầu tiên trong khai triển của để tính gần đúng và ứng dụng (nếu có)
5.1. Phương pháp giải
Ta có khai triển và tính giá trị gần đúng dùng 2 số hạng đầu tiên như sau:
5.2. Ví dụ
Ví dụ 1. Dùng hai số hạng đầu tiên trong khai triển để tính gần đúng số (2,01)5. Tìm số đó.
A. 32,808.
B. 32,80804.
C. 32,8.
D. 32,8080401.
Hướng dẫn giải
Ví dụ 2. Số dân ở thời điểm hiện tại của một tỉnh là 1 triệu người. Tỉ lệ tăng dân số hàng năm của tỉnh đó là 5%. Sử dụng hai số hạng đầu tiên trong khai triển của lũy thừa (a + b)n, hỏi sau bao nhiêu năm thì số dân của tỉnh đó là 1,2 triệu người?
|
Điền đáp án |
|
Hướng dẫn giải
Gọi A là số dân ban đầu, ra là tỉ lệ tăng dân số hàng năm, An là số dân của tỉnh đó sau n năm.
Khi đó An = A(1 + r)n, với r = 5% là tỉ lệ tăng dân số hàng năm.
Theo giả thiết:
Vậy sau khoảng 4 năm thì số dân của tỉnh đó là 1,2 triệu người.
Điền đáp án: 4.
III. CÂU HỎI VẬN DỤNG
Dạng 1. Câu trắc nghiệm nhiều phương án chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Tính tổng các hệ số trong khai triển nhị thức Newton của (1 - 2x)4.
A. 1.
B. -1.
C. 81.
D. -81.
Câu 2. Gọi n là số nguyên dương thỏa mãn . Tìm hệ số của x3 trong khai triển nhị thức Newton của (1 - 3x)n.
A. -108.
B. 81.
C. 54.
D. -12.
Câu 3. Tìm số hạng không chứa x trong khai triển nhị thức Newton của .
A. 1.
B. 4.
C. 6.
D. 12.
Câu 4. Tìm hệ số của đơn thức a3b2 trong khai triển nhị thức (a + 2b)5.
A. 160.
B. 80.
C. 20.
D. 40.
Câu 5. Biết . Tính a1a2.
A. a1a2 = 24.
B. a1a2 = 8.
C. a1a2 = 54.
D. a1a2 = 36.
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Tập hợp
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đường tròn trong mặt phẳng tọa độ
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Hàm số lượng giác và phương trình lượng giác
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Cấp số cộng. Cấp số nhân
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Giới hạn. Hàm số liên tục
- (Ôn thi ĐGNL, ĐGTD) Chuyên đề: Lũy thừa - Mũ - Logarit
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều


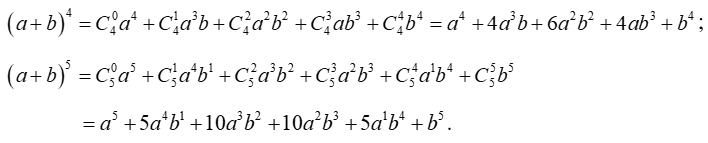
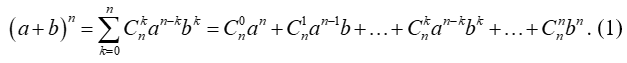
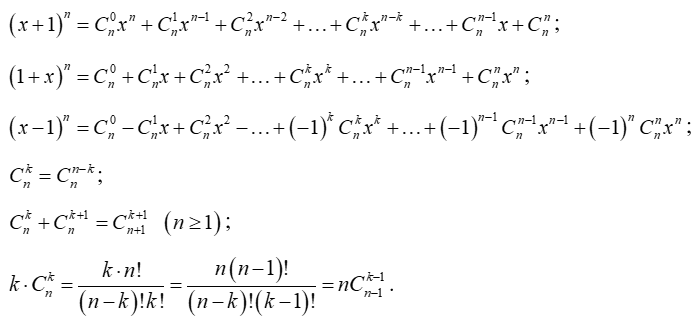
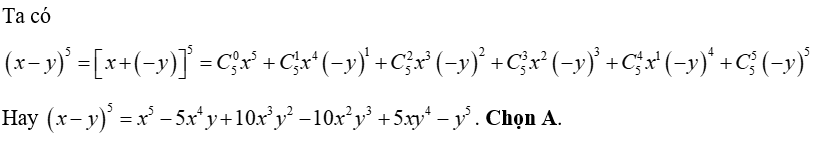
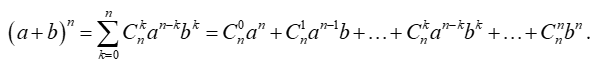
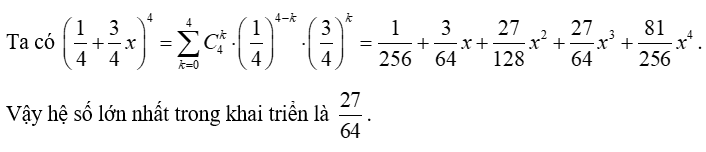
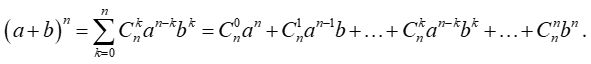
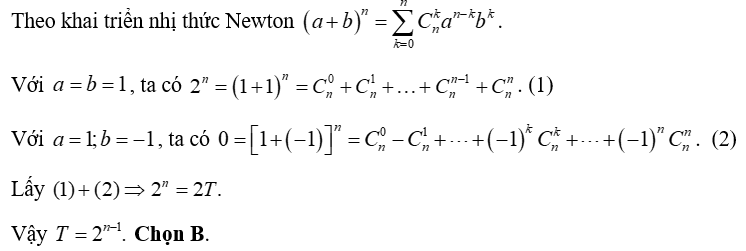
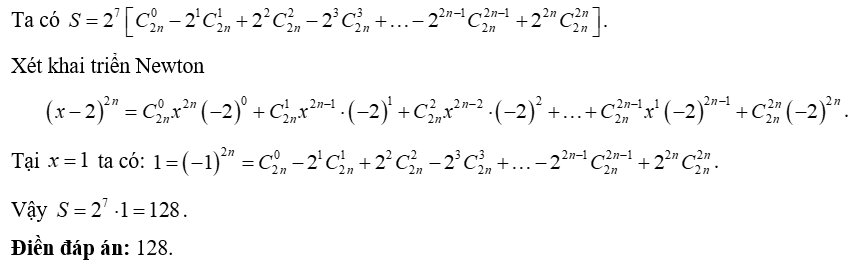
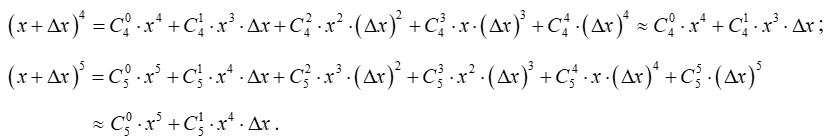
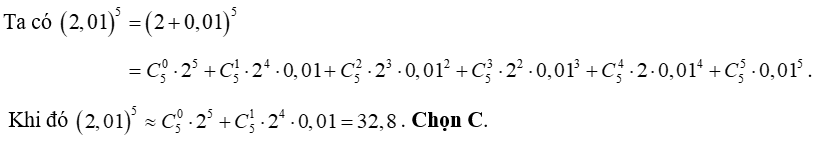
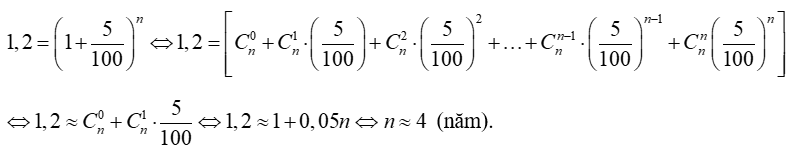



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

